Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 7, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 6 Cánh diều, bao gồm các dạng bài tập đa dạng, bám sát kiến thức trọng tâm.
Với đáp án chi tiết đi kèm, học sinh có thể tự kiểm tra và rút kinh nghiệm sau khi làm bài, từ đó nâng cao kết quả học tập.
Trong cách viết sau, cách viết nào cho ta phân số?
Số đối của phân số \( - \frac{{16}}{{25}}\) là:
Phân số nào sau đây bằng phân số \(\frac{3}{4}\)?
Tìm số nguyên \(y\) biết \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\).
Trong trò chơi “Hộp quà bí mật”, có 5 hộp quà giống nhau về kích thước và màu sắc, mỗi chiếc hộp chứa một phần thưởng khác nhau gồm: 1 bông hoa, 1 cây bút mực, 1 quyển truyện, 1 quyển vở, 1 cây thước. Lấy ngẫu một hộp quà, hỏi có bao nhiêu kết quả có thể xảy ra với phần quà trong hộp?
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Nhơn Khánh.
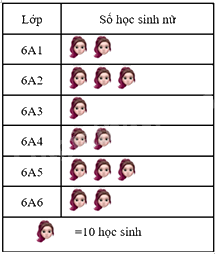
Chọn đáp án đúng
Trong cuộc khảo sát về họ của 32 học sinh lớp 6A, giáo viên lập được bảng thống kê như sau:

Hỏi ở lớp 6A, họ nào có nhiều số học sinh nhất?
Bạn Sơn tung đồng xu 50 lần thấy có 30 lần xuất hiện mặt \(S\) còn bạn Tùng tung 100 lần và thấy có 55 lần xuất hiện mặt \(S\). Bạn Sơn nói xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{30}}{{50}}\); còn bạn Tùng bảo rằng xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{55}}{{100}}\). Vậy trong hai bạn thì bạn nào nói đúng?
Cho hình vẽ

Số giao điểm tạo bởi 4 đường thẳng trong hình trên là:
Chọn phát biểu đúng trong các phát biểu sau:
Qua 2 điểm phân biệt ta vẽ được:
Chohình vẽ. Hai tia nào đối nhau?
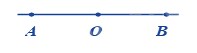
Trong hình vẽ sau đây có bao nhiêu đoạn thẳng?

Thực hiện các phép tính (tính hợp lí nếu có thể):
a) A = \(\frac{1}{2}\)+\(\frac{1}{3}\)
b) \(B = \frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}\)
c) \(C = \frac{{25}}{6}:\frac{5}{3} - \left( {\frac{{ - 1}}{4}} \right)\)
Biểu đồ dưới đây cho biết số ca nhiễm Covid – 19 của một số địa phương tại tỉnh Bình Định từ 6h00 ngày 10/3/2022 đến 6h00 ngày 11/3/2022. Dựa vào biểu đồ trả lời các câu hỏi sau:
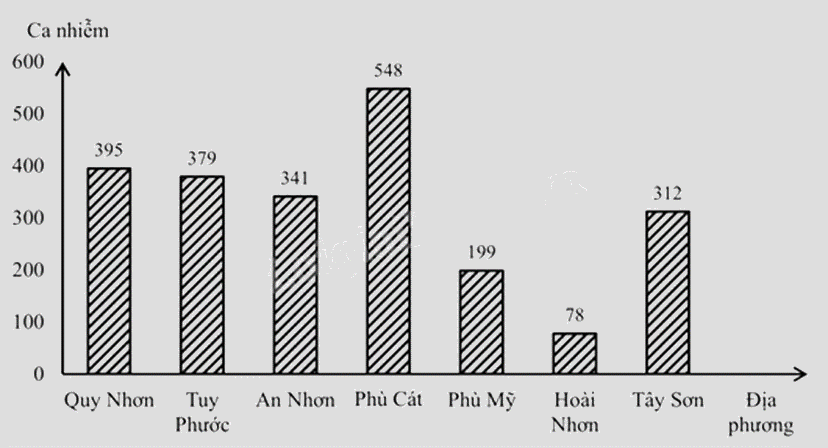
a) Địa phương nào có số ca nhiễm Covid – 19 nhiều nhất? Số ca nhiễm Covid – 19 ở Phù Cát nhiều hơn số ca nhiễm Covid – 19 ở Hoài Nhơn và Tây Sơn là bao nhiêu ca nhiễm?
b) Tính tổng số ca nhiễm Covid – 19 của các địa phương tại tỉnh Bình Định thống kê ở trên từ 6h00 ngày 10/3/2022 đến 6h00 ngày 11/3/2022.
Một chiếc hộp có 6 con Gấu bông có kích thước và khối lượng giống nhau, các Gấu bông có màu sắc khác nhau gồm các màu: Đỏ, Xanh, Vàng, Trắng, Hồng, Đen. Lấy ngẫu nhiên một con Gấu bông trong hộp, sau đó xem màu rồi trả lại trong hộp.
a) Có bao nhiêu kết quả có thể xảy ra với màu của con Gấu bông được lấy ra? Viết tập hợp các kết quả đối với màu của con Gấu bông được lấy ra.
b) Lặp lại hoạt động lấy ngẫu nhiên một con Gấu bông trong hộp 40 lần, trong đó có 10 lần lấy được con gấu có màu Hồng. Xác suất thực nghiệm lấy được con Gấu bông màu Hồng là bao nhiêu?
Cho \(Ox\) và \(Oy\) là hai tia đối nhau. Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA = 6cm\). Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB = 3cm\). Gọi \(M,N\) lần lượt là trung điểm của \(OA,OB\).
a) Tính \(OM,{\rm{ }}ON\)?
b) Tính độ dài đoạn thẳng \(MN\)?
a) Tính tổng \(A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}}\).
b) Chứng minh \(M = \frac{{n - 1}}{{n - 2}}\,\,\,\left( {n \in {\rm Z}\,;\,n \ne 2} \right)\) là phân số tối giản.
Trong cách viết sau, cách viết nào cho ta phân số?
Đáp án : A
Dựa vào khái niệm về phân số.
\(\frac{{0,25}}{{ - 3}}\) không phải phân số vì \(0,25 \notin \mathbb{Z}\).
\(\frac{5}{0}\) không phải phân số vì 0 nằm ở mẫu.
\(\frac{{6,23}}{{7,4}}\) không phải phân số vì \(6,23;7,4 \notin \mathbb{Z}\).
\(\frac{4}{7}\) là phân số vì \(4;7 \in \mathbb{Z};7 \ne 0\).
Đáp án A.
Số đối của phân số \( - \frac{{16}}{{25}}\) là:
Đáp án : A
Số đối của phân số \(\frac{a}{b}\) là phân số \( - \frac{a}{b}\).
Số đối của phân số \( - \frac{{16}}{{25}}\) là\(\frac{{16}}{{25}}\).
Đáp án A.
Phân số nào sau đây bằng phân số \(\frac{3}{4}\)?
Đáp án : C
Sử dụng quy tắc nhân cả tử và mẫu của một phân số: Nếu ta nhân cả tử và mẫu của một phân số với cùng 1 số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
Ta có: \(\frac{3}{4} = \frac{{3.2}}{{4.2}} = \frac{6}{8}\) nên phân số \(\frac{6}{8} = \frac{3}{4}\).
Đáp án C.
Tìm số nguyên \(y\) biết \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\).
Đáp án : D
Hai phân số \(\frac{a}{b} = \frac{c}{d}\) nếu ad = bc.
Ta có: \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\) nên
\(\begin{array}{l}2.\left( { - y} \right) = 6.\left( { - 3} \right)\\ - 2y = - 18\\y=(-18):(-2)\\y = 9\end{array}\)
Đáp án D.
Trong trò chơi “Hộp quà bí mật”, có 5 hộp quà giống nhau về kích thước và màu sắc, mỗi chiếc hộp chứa một phần thưởng khác nhau gồm: 1 bông hoa, 1 cây bút mực, 1 quyển truyện, 1 quyển vở, 1 cây thước. Lấy ngẫu một hộp quà, hỏi có bao nhiêu kết quả có thể xảy ra với phần quà trong hộp?
Đáp án : B
Dựa vào mô hình trò chơi lấy ngẫu nhiên.
Có 5 kết quả có thể xảy ra đó là: 1 bông hoa, 1 cây bút mực, 1 quyển truyện, 1 quyển vở, 1 cây thước.
Đáp án B.
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Nhơn Khánh.
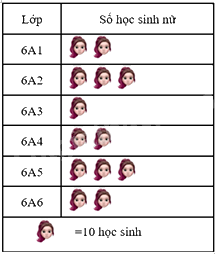
Chọn đáp án đúng
Đáp án : C
Quan sát biểu đồ để trả lời.
Lớp 6A3 có ít học sinh nữ nhất nên A sai.
Lớp 6A5 có nhiều học sinh nữ hơn lớp 6A4 (30 > 20) nên B sai.
Lớp 6A6 có 20 học sinh nữ nên C đúng (2.10 = 20)
Tổng số học sinh nữ là: 2.10 + 3.10 + 1.10 + 2.10 + 3.10 + 2.10 = 130 nên D sai.
Đáp án C.
Trong cuộc khảo sát về họ của 32 học sinh lớp 6A, giáo viên lập được bảng thống kê như sau:

Hỏi ở lớp 6A, họ nào có nhiều số học sinh nhất?
Đáp án : C
Quan sát bảng thống kê để trả lời.
Quan sát bảng thống kê ta thấy họ Nguyễn có nhiều học sinh nhất (12 học sinh).
Đáp án C.
Bạn Sơn tung đồng xu 50 lần thấy có 30 lần xuất hiện mặt \(S\) còn bạn Tùng tung 100 lần và thấy có 55 lần xuất hiện mặt \(S\). Bạn Sơn nói xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{30}}{{50}}\); còn bạn Tùng bảo rằng xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{55}}{{100}}\). Vậy trong hai bạn thì bạn nào nói đúng?
Đáp án : C
Tình huống thực nghiệm khác nhau thì có thể thu được xác suất thực nghiệm khác nhau.
Cả hai bạn đều đúng. Vì mỗi tình huống thực nghiệm sẽ cho một xác suất thực nghiệm (có thể không giống nhau)
Đáp án C.
Cho hình vẽ

Số giao điểm tạo bởi 4 đường thẳng trong hình trên là:
Đáp án : D
Quan sát hình vẽ để trả lời.
Có 4 giao điểm tạo bởi 4 đường thẳng trong hình trên.
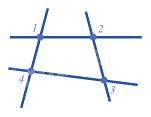
Đáp án D.
Chọn phát biểu đúng trong các phát biểu sau:
Qua 2 điểm phân biệt ta vẽ được:
Đáp án : A
Dựa vào kiến thức về điểm và đường thẳng.
Qua hai điểm phân biệt ta chỉ vẽ được 1 đường thẳng nên A đúng.
Đáp án A.
Chohình vẽ. Hai tia nào đối nhau?
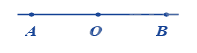
Đáp án : A
Dựa vào kiến thức về tia.
Hai tia OA và OB là hai tia đối nhau.
Đáp án A.
Trong hình vẽ sau đây có bao nhiêu đoạn thẳng?

Đáp án : D
Dựa vào kiến thức về đoạn thẳng.
Có 6 đoạn thẳng trong hình vẽ, đó là: KJ, KL, KN, JL, JN, LN.
Đáp án D.
Thực hiện các phép tính (tính hợp lí nếu có thể):
a) A = \(\frac{1}{2}\)+\(\frac{1}{3}\)
b) \(B = \frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}\)
c) \(C = \frac{{25}}{6}:\frac{5}{3} - \left( {\frac{{ - 1}}{4}} \right)\)
Dựa vào các quy tắc tính với phân số.
a) A = \(\frac{1}{2}\) + \(\frac{1}{3}\) = \(\frac{3}{6} + \frac{2}{6} = \frac{5}{6}\)
b) B = \(\frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}\)\( = \left( {\frac{{ - 3}}{7} - \frac{4}{7}} \right) + \left( {\frac{5}{{14}} + \frac{9}{{14}}} \right) + \frac{3}{{12}}\)\( = - 1 + 1 + \frac{3}{{12}}\) \( = \frac{3}{{12}}\) = \(\frac{1}{4}\)
c) \(C = \frac{{25}}{6}:\frac{5}{3} - \left( {\frac{{ - 1}}{4}} \right)\)\( = \frac{{25}}{6}.\frac{3}{5} + \frac{1}{4}\)\( = \frac{5}{2} + \frac{1}{4}\)\( = \frac{{10}}{4} + \frac{1}{4} = \frac{{11}}{4}\)
Biểu đồ dưới đây cho biết số ca nhiễm Covid – 19 của một số địa phương tại tỉnh Bình Định từ 6h00 ngày 10/3/2022 đến 6h00 ngày 11/3/2022. Dựa vào biểu đồ trả lời các câu hỏi sau:
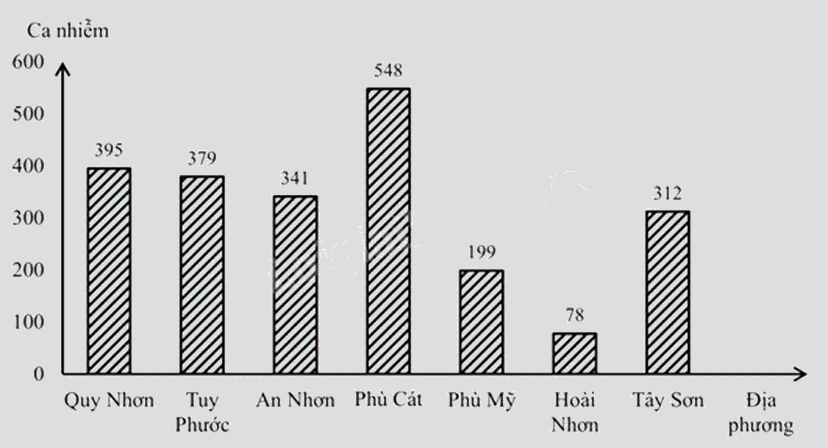
a) Địa phương nào có số ca nhiễm Covid – 19 nhiều nhất? Số ca nhiễm Covid – 19 ở Phù Cát nhiều hơn số ca nhiễm Covid – 19 ở Hoài Nhơn và Tây Sơn là bao nhiêu ca nhiễm?
b) Tính tổng số ca nhiễm Covid – 19 của các địa phương tại tỉnh Bình Định thống kê ở trên từ 6h00 ngày 10/3/2022 đến 6h00 ngày 11/3/2022.
Quan sát biểu đồ để trả lời câu hỏi.
a) Địa phương có số ca nhiễm Covid – 19 là Phù Cát (548 ca nhiễm)
Số ca nhiễm Covid – 19 ở Phù Cát nhiều hơn số ca nhiễm Covid – 19 ở Hoài Nhơn và Tây Sơn là:
\(548 - (78 + 312) = 158\)(Ca nhiễm)
b) Tổng số ca nhiễm Covid – 19 của một số địa phương tại tỉnh Bình Định từ 6h00 ngày 10/3/2022 đến 6h00 ngày 11/3/2022.
\(395 + 379 + 341 + 548 + 199 + 79 + 312 = 2253\)(Ca nhiễm)
Một chiếc hộp có 6 con Gấu bông có kích thước và khối lượng giống nhau, các Gấu bông có màu sắc khác nhau gồm các màu: Đỏ, Xanh, Vàng, Trắng, Hồng, Đen. Lấy ngẫu nhiên một con Gấu bông trong hộp, sau đó xem màu rồi trả lại trong hộp.
a) Có bao nhiêu kết quả có thể xảy ra với màu của con Gấu bông được lấy ra? Viết tập hợp các kết quả đối với màu của con Gấu bông được lấy ra.
b) Lặp lại hoạt động lấy ngẫu nhiên một con Gấu bông trong hộp 40 lần, trong đó có 10 lần lấy được con gấu có màu Hồng. Xác suất thực nghiệm lấy được con Gấu bông màu Hồng là bao nhiêu?
a) Xác định các kết quả có thể xảy ra.
b) Xác suất thực nghiệm xuất hiện màu A khi lấy nhiều lần bằng tỉ số giữa số lần màu A xuất hiện với tổng số lần lấy.
a) Có 6 kết quả có thể xảy ra với màu của con Gấu bông được lấy ra, đó là: Đỏ, Xanh, Vàng, Trắng, Hồng, Đen.
Tập hợp các kết quả đối với màu của con Gấu bông được lấy ra là:
{Đỏ, Xanh, Vàng, Trắng, Hồng, Đen}.
b) Xác suất thực nghiệm lấy được con gấu bông màu Hồng là: \(\frac{{10}}{{40}} = \frac{1}{4}\).
Cho \(Ox\) và \(Oy\) là hai tia đối nhau. Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA = 6cm\). Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB = 3cm\). Gọi \(M,N\) lần lượt là trung điểm của \(OA,OB\).
a) Tính \(OM,{\rm{ }}ON\)?
b) Tính độ dài đoạn thẳng \(MN\)?
Vẽ hình theo yêu cầu đề bài.
a) Sử dụng tính chất của trung điểm để tìm OM, ON.
b) Vì O nằm giữa MN nên MN = OM + ON.

a) Do \(M\) là trung điểm của \(OA\) nên ta có:
\(OM = MA = \frac{{OA}}{2} = \frac{6}{2} = 3(cm)\)
Do \(N\) là trung điểm của \(OB\) nên ta có:
\(ON = NB = \frac{{OB}}{2} = \frac{3}{2} = 1,5(cm)\)
b) Vì điểm \(O\) nằm giữa hai điểm \(M,N\) nên ta có: \(MN = OM + ON\)
Suy ra \(MN = 3 + 1,5 = 4,5(cm)\)
Vậy \({\rm{MN = 4,5 cm}}\).
a) Tính tổng \(A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}}\).
b) Chứng minh \(M = \frac{{n - 1}}{{n - 2}}\,\,\,\left( {n \in {\rm Z}\,;\,n \ne 2} \right)\) là phân số tối giản.
a) Nhân cả tử và mẫu của các phân số trong A với 2.
Rút 2 ra ngoài, biến đổi các phân số \(\frac{1}{{a\left( {a + 1} \right)}}\) thành \(\frac{1}{a} - \frac{1}{{a + 1}}\) (vì \(\frac{1}{{a\left( {a + 1} \right)}} = \frac{1}{a} - \frac{1}{{a + 1}}\))
Tính A.
b) Để chứng minh phân số tổi giản, ta chứng minh ƯCLN của tử số và mẫu số là 1.
a) Ta có \(A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}} = \frac{2}{6} + \frac{2}{{12}} + \frac{2}{{20}} + \frac{2}{{30}} + ... + \frac{2}{{90}}\)
\(\begin{array}{l} = 2\left( {\frac{1}{{2.3}} + \frac{1}{{3.4}} + \frac{1}{{4.5}} + \frac{1}{{5.6}} + ... + \frac{1}{{9.10}}} \right)\\ = 2\left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + \frac{1}{5} - \frac{1}{6} + ... + \frac{1}{9} - \frac{1}{{10}}} \right)\end{array}\)
\( = 2\left( {\frac{1}{2} - \frac{1}{{10}}} \right) = 2.\frac{4}{{10}} = \frac{4}{5}\).
Vậy \(A = \frac{4}{5}.\)
b) Gọi ƯCLN\(\left( {n - 1\,;\,n - 2} \right) = d\) suy ra \(n - 1 \vdots d\,\,\,,\,\,n - 2 \vdots d\)
suy ra \(\left( {n - 1} \right) - \left( {n - 2} \right) \vdots d\)suy ra \(1 \vdots d \Rightarrow d = 1\) với mọi \(n\)
Vậy với mọi \(n \in {\rm Z}\) thì \(M = \frac{{n - 1}}{{n - 2}}\) là phân số tối giản.
Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 7 là một bài kiểm tra đánh giá kiến thức và kỹ năng giải toán của học sinh sau khi hoàn thành chương trình học kì 2. Đề thi thường bao gồm các nội dung chính sau:
Cấu trúc đề thi thường bao gồm các dạng bài tập khác nhau như trắc nghiệm, tự luận, bài toán thực tế. Thời gian làm bài thường là 60-90 phút.
Để giúp học sinh làm quen với cấu trúc và nội dung đề thi, chúng ta sẽ đi vào phân tích chi tiết Đề số 7:
Phần trắc nghiệm thường chiếm khoảng 30-40% tổng số điểm. Các câu hỏi trắc nghiệm thường kiểm tra kiến thức cơ bản, khả năng nhận biết và vận dụng các khái niệm toán học. Ví dụ:
Phần tự luận thường chiếm khoảng 60-70% tổng số điểm. Các bài toán tự luận yêu cầu học sinh trình bày lời giải chi tiết, rõ ràng, logic. Ví dụ:
Để đạt kết quả tốt trong kỳ thi giữa kì 2 Toán 6 Cánh diều, học sinh cần có kế hoạch ôn tập khoa học và hợp lý. Dưới đây là một số gợi ý:
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài tập, đề thi và đáp án chi tiết cho học sinh Toán 6. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em nắm vững kiến thức và đạt kết quả cao trong học tập.
Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 7 là một bài kiểm tra quan trọng, đánh giá năng lực học tập của học sinh. Hy vọng với những thông tin và gợi ý trên, các em sẽ có một kỳ thi thành công. Chúc các em học tốt!