Bài toán chuyển động cùng chiều là một trong những dạng toán phổ biến trong chương trình Vật lý và Toán học cấp THCS. Việc nắm vững công thức làm bài toán chuyển động cùng chiều sẽ giúp học sinh giải quyết các bài tập một cách nhanh chóng và chính xác.
Giaitoan.edu.vn cung cấp các bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng, giúp bạn hiểu sâu sắc về kiến thức này.
Công thức làm bài toán chuyển động cùng chiều - Công thức toán 5
1. Hai vật chuyển động cùng chiều, xuất phát cùng một thời điểm Xe thứ nhất có vận tốc v1, xe thứ hai có vận tốc v2 (coi v1 > v2) Hai xe xuất phát cùng lúc từ hai vị trí cách nhau quãng đường là S
2. Hai vật chuyển động cùng chiều, xuất phát khác thời điểm ở cùng một vị trí Hai xe chuyển động cùng chiều, xuất phát từ cùng 1 vị trí. Xe thứ hai xuất phát trước xe thứ nhất thời gian tO, sau đó xe thứ nhất đuổi theo thì thời gian đuổi kịp nhau là:
|
Ví dụ 1: Lúc 12 giờ trưa một ô tô xuất phát từ A với vận tốc 60 km/giờ để đi đến B. Cùng lúc đó từ địa điểm C trên đường từ A đến B và cách A 40km, một người đi xe máy với vận tốc 45 km/giờ cũng đi về B. Hỏi lúc mấy giờ thì hai xe gặp nhau và chỗ gặp nhau cách A bao xa?
Giải
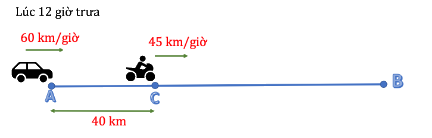
Hiệu vận tốc của hai xe là
60 – 45 = 15 (km)
Thời gian để ô tô đuổi kịp xe máy là:
40 : 15 = giờ = 2 giờ 40 phút
Thời điểm hai xe gặp nhau là:
12 giờ + 2 giờ 40 phút = 14 giờ 40 phút
Đổi 2 giờ 40 phút = $\frac{8}{3}$ giờ
Quãng đường từ A đến địa điểm gặp nhau là:60 x $\frac{8}{3}$ = 160 (km)
Đáp số: 14 giờ 40 phút; 160km
Ví dụ 2: Lúc 6 giờ một ô tô chở hàng đi từ A với vận tốc 45 km/giờ. Đến 8 giờ một ô tô du lịch cũng đi từ A với vận tốc 60 km/giờ và đi cùng chiều với ô tô chở hàng. Hỏi đến mấy giờ thì ô tô du lịch đuổi kịp ô tô chở hàng?
Giải:
Thời gian ô tô chở hàng đi trước ô tô du lịch là
8 – 6 = 2 (giờ)
Quãng đường ô tô chở hàng đi trước ô tô du lịch là
45 x 2 = 90 (km)
Thời gian để 2 xe gặp nhau là
90 : (60 – 45) = 6 (giờ)
Thời điểm ô tô du lịch đuổi kịp ô tô chở hàng là
8 + 6 = 14 (giờ)
Đáp số: 14 giờ
Chuyển động cùng chiều là chuyển động mà các vật thể di chuyển theo cùng một hướng trên một đường thẳng. Để giải các bài toán liên quan đến chuyển động cùng chiều, chúng ta cần hiểu rõ các khái niệm cơ bản như vận tốc, quãng đường, thời gian và mối quan hệ giữa chúng.
Dưới đây là các công thức quan trọng nhất khi giải bài toán chuyển động cùng chiều:
Có nhiều dạng bài tập liên quan đến chuyển động cùng chiều, nhưng phổ biến nhất là:
Để giải bài toán gặp nhau, ta có thể sử dụng công thức sau:
s1 + s2 = s (trong đó s1 là quãng đường vật 1 đi được, s2 là quãng đường vật 2 đi được, s là tổng quãng đường)
Ngoài ra, ta cũng có thể sử dụng công thức:
t1 = t2 = t (thời gian hai vật gặp nhau là như nhau)
Để giải bài toán đuổi kịp, ta có thể sử dụng công thức sau:
s1 = s2 + d (trong đó s1 là quãng đường vật đuổi kịp đi được, s2 là quãng đường vật bị đuổi kịp đi được, d là khoảng cách ban đầu giữa hai vật)
Ngoài ra, ta cũng có thể sử dụng công thức:
t1 = t2 + t0 (thời gian vật đuổi kịp đi được bằng thời gian vật bị đuổi kịp đi được cộng với thời gian vật đuổi kịp xuất phát sau)
Ví dụ 1: Hai ô tô xuất phát cùng lúc từ hai địa điểm A và B cách nhau 120km, đi ngược chiều nhau. Ô tô thứ nhất có vận tốc 40km/h, ô tô thứ hai có vận tốc 60km/h. Hỏi sau bao lâu hai ô tô gặp nhau?
Giải:
Gọi t là thời gian hai ô tô gặp nhau.
Quãng đường ô tô thứ nhất đi được là: s1 = 40t
Quãng đường ô tô thứ hai đi được là: s2 = 60t
Tổng quãng đường hai ô tô đi được là: s1 + s2 = 120km
Thay vào, ta có: 40t + 60t = 120
=> 100t = 120
=> t = 1.2 giờ
Vậy hai ô tô gặp nhau sau 1.2 giờ.
Để củng cố kiến thức về công thức làm bài toán chuyển động cùng chiều, bạn có thể thực hành giải các bài tập sau:
Việc nắm vững công thức làm bài toán chuyển động cùng chiều là rất quan trọng đối với học sinh THCS. Hy vọng rằng, với những kiến thức và ví dụ minh họa trên, bạn sẽ tự tin hơn khi giải các bài tập liên quan đến chủ đề này. Hãy luyện tập thường xuyên để đạt kết quả tốt nhất!