Diện tích hình tam giác là một khái niệm cơ bản và quan trọng trong hình học. Việc nắm vững công thức tính diện tích hình tam giác không chỉ giúp bạn giải quyết các bài toán trong học tập mà còn ứng dụng trong nhiều lĩnh vực thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp một hướng dẫn chi tiết và dễ hiểu về các công thức tính diện tích hình tam giác, kèm theo các ví dụ minh họa và bài tập thực hành để bạn có thể tự tin áp dụng kiến thức vào giải quyết các vấn đề.
Công thức tính diện tích hình tam giác - Công thức Toán 5
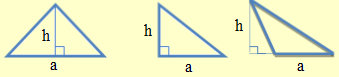
Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
$S = \frac{{a \times h}}{2}$hoặc S = a x h : 2 (S là diện tích, a là độ dài đáy, h là chiều cao) |
Ví dụ 1: Tính diện tích hình tam giác có độ dài đáy là 2m và chiều cao là 15dm.
Giải
Đổi 2m = 20 dm
Diện tích hình tam giác đó là:
20 x 15 : 2 = 150 (dm2)
Đáp số: 150 dm2
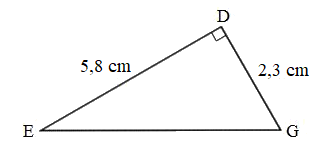
Ví dụ 2: Tính diện tích hình tam giác vuông DEG.
Giải
Diện tích hình tam giác DEG là:
$\frac{{5,8 \times 2,3}}{2} = 6,67$ (cm2)
Đáp số: 6,67 cm2
Diện tích hình tam giác là lượng không gian bên trong hình tam giác, được đo bằng đơn vị bình phương (ví dụ: cm², m², inch²). Có nhiều công thức khác nhau để tính diện tích hình tam giác, tùy thuộc vào thông tin đã biết về tam giác đó.
Đây là công thức cơ bản và được sử dụng phổ biến nhất:
Diện tích (S) = (1/2) * đáy (b) * chiều cao (h)
Trong đó:
Nếu bạn biết độ dài ba cạnh của tam giác (a, b, c), bạn có thể sử dụng công thức Heron để tính diện tích:
S = √(p(p-a)(p-b)(p-c))
Trong đó:
Nếu bạn biết độ dài hai cạnh (a, b) và góc xen giữa chúng (C), bạn có thể sử dụng công thức:
S = (1/2) * a * b * sin(C)
Tam giác đều là tam giác có ba cạnh bằng nhau. Nếu cạnh của tam giác đều là a, diện tích của nó là:
S = (a² * √3) / 4
Ví dụ 1: Một tam giác có đáy là 10cm và chiều cao là 5cm. Tính diện tích của tam giác đó.
Giải:
S = (1/2) * 10cm * 5cm = 25cm²
Ví dụ 2: Một tam giác có ba cạnh là 3cm, 4cm và 5cm. Tính diện tích của tam giác đó.
Giải:
p = (3cm + 4cm + 5cm) / 2 = 6cm
S = √(6cm(6cm-3cm)(6cm-4cm)(6cm-5cm)) = √(6cm * 3cm * 2cm * 1cm) = √36cm⁴ = 6cm²
Công thức tính diện tích hình tam giác có nhiều ứng dụng trong thực tế, bao gồm:
Việc hiểu và áp dụng các công thức tính diện tích hình tam giác là rất quan trọng trong học tập và cuộc sống. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin giải quyết các bài toán liên quan đến diện tích hình tam giác.