Hình thoi là một hình học quen thuộc trong chương trình toán học, đặc biệt là ở cấp tiểu học và trung học cơ sở. Việc nắm vững công thức tính diện tích hình thoi là vô cùng quan trọng để giải quyết các bài toán liên quan đến hình học. Bài viết này sẽ cung cấp cho bạn một cách đầy đủ và dễ hiểu nhất về công thức này, cùng với các ví dụ minh họa và bài tập thực hành.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng mang đến những kiến thức toán học chất lượng và dễ tiếp cận nhất cho học sinh và những người yêu thích môn học này.
Công thức tính diện tích hình thoi - Công thức Toán 5
1. Hình thoi
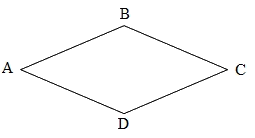
Hình thoi ABCD có:
- Cạnh AB song song với cạnh DC.
Cạnh AD song song với cạnh BC.
- AB = BC = CD = AD.
Hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
2. Diện tích hình thoi
Diện tích hình thoi bằng tích của độ dài hai đường chéo chia cho 2 (cùng một đơn vị đo) $S = \frac{{m \times n}}{2}$ (S là diện tích của hình thoi; m, n là độ dài của hai đường chéo) |
Ví dụ 1: Một mảnh bìa hình thoi có độ dài các đường chéo là 12 cm và 26 cm. Tính diện tích mảnh bìa đó?
Giải
Diện tích của mảnh bìa là
$\frac{{12 \times 26}}{2} = 156$ (cm2)
Đáp số: 156 cm2
Ví dụ 2: Một hình thoi có diện tích 350 dm2, dộ dài một đường chéo là 25 dm. Tính độ dài đường chéo thứ hai.
Giải
Độ dài đường chéo thứ hai là
350 x 2 : 25 = 28 (dm)
Đáp số: 28 dm
Diện tích hình thoi là phần không gian bên trong hình thoi, được đo bằng đơn vị diện tích (ví dụ: cm², m², inch²,...). Để tính diện tích hình thoi, chúng ta có thể sử dụng một trong hai công thức sau:
Diện tích hình thoi = (1/2) * d1 * d2
Trong đó:
Công thức này dựa trên việc chia hình thoi thành bốn tam giác vuông bằng nhau. Diện tích mỗi tam giác vuông là (1/2) * (d1/2) * (d2/2). Tổng diện tích của bốn tam giác vuông này chính là diện tích của hình thoi.
Diện tích hình thoi = a² * sin(α)
Trong đó:
Công thức này dựa trên việc xem hình thoi như một hình bình hành đặc biệt. Diện tích hình bình hành được tính bằng tích của hai cạnh kề và sin của góc giữa chúng.
Ví dụ 1: Một hình thoi có độ dài hai đường chéo là 8cm và 6cm. Tính diện tích của hình thoi đó.
Giải:
Áp dụng công thức Diện tích = (1/2) * d1 * d2, ta có:
Diện tích = (1/2) * 8cm * 6cm = 24cm²
Ví dụ 2: Một hình thoi có cạnh dài 5cm và góc nhọn 60°. Tính diện tích của hình thoi đó.
Giải:
Áp dụng công thức Diện tích = a² * sin(α), ta có:
Diện tích = 5² * sin(60°) = 25 * (√3/2) ≈ 21.65cm²
Diện tích hình thoi có mối liên hệ mật thiết với diện tích của các hình khác, chẳng hạn như:
Công thức tính diện tích hình thoi có nhiều ứng dụng trong thực tế, chẳng hạn như:
Khi tính diện tích hình thoi, cần lưu ý:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về công thức tính diện tích hình thoi. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.