Hình hộp chữ nhật là một trong những hình khối cơ bản và quan trọng trong chương trình học Toán. Việc nắm vững công thức tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật là nền tảng để giải quyết các bài toán thực tế và nâng cao kiến thức hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài học chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng giúp bạn hiểu rõ và áp dụng thành thạo các công thức này.
Công thức tính diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật - Công thức Toán 5
1. Hình hộp chữ nhật
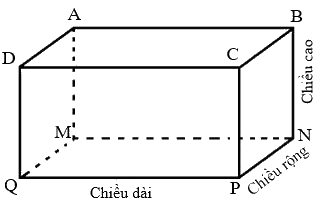
Hình hộp chữ nhật có:
- 6 mặt: 2 mặt đáy và 4 mặt bên đều là hình chữ nhật
- 8 đỉnh: đỉnh A, đỉnh B, đỉnh C, đỉnh D, đỉnh M, đỉnh N, đỉnh P, đỉnh Q.
- 12 cạnh: cạnh AB, cạnh BC, cạnh CD, cạnh DA, cạnh MN, cạnh NP, cạnh PQ, cạnh MQ, cạnh AM, cạnh BN, cạnh CP, cạnh DQ.
2. Diện tích xung quanh
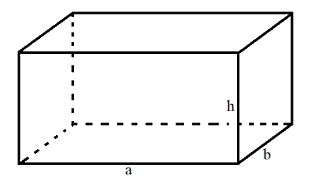
Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.
Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo) ${S_{xq}} = (a + b) \times 2 \times h$ |
3. Diện tích toàn phần
Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy Stoàn phần = Sxung quanh + Sđáy x 2 |
Ví dụ 1: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 8cm, chiều rộng 6cm và chiều cao 4cm.
Bài giải
Chu vi đáy của hình hộp chữ nhật là:
(8 + 6) × 2 = 28 (cm)
Diện tích xung quanh của hình hộp chữ nhật đó là:
28 × 4 = 112 (cm2)
Diện tích một đáy là:
8 × 6 = 48 (cm2)
Diện tích toàn phần của hình hộp chữ nhật đó là:
112 + 48 × 2 = 208(cm2)
Đáp số: Diện tích xung quanh: 112cm2
Diện tích toàn phần: 208cm2
Ví dụ 2: Cho hình hộp chữ nhật có diện tích xung quanh là 217,5m2 và nửa chu vi mặt đáy bằng 14,5m. Tính chiều cao của hình hộp chữ nhật đó.
Giải
Chu vi mặt đáy của hình hộp chữ nhật đó là:
14,5 × 2 = 29 (m)
Chiều cao của hình hộp chữ nhật đó là:
217,5 : 29 = 7,5 (m)
Đáp số: 7,5m
Ví dụ 3: Một căn phòng dạng hình hộp chữ nhật có chiều dài 6m, chiều rộng 48dm, chiều cao 4m. Người ta muốn quét vôi các bức tường xung quanh và trần của căn phòng đó. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết tổng diện tích các cửa bằng 12m2 (biết rằng chỉ quét vôi bên trong phòng)?
Giải
Đổi 48dm = 4,8m
Diện tích xung quanh của căn phòng đó là:
(6 + 4,8) × 2 × 4 = 86,4 (m2)
Diện tích trần của căn phòng đó là:
6 × 4,8 = 28,8 (m2)
Diện tích cần quét vôi là:
86,4 + 28,8 – 12 = 103,2 (m2)
Đáp số: 103,2m2
Hình hộp chữ nhật là một hình khối có sáu mặt, trong đó mỗi mặt là một hình chữ nhật. Để tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật, chúng ta cần hiểu rõ các khái niệm và công thức liên quan.
Một hình hộp chữ nhật được xác định bởi ba kích thước chính:
Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích của bốn mặt bên. Công thức tính diện tích xung quanh (Sxq) như sau:
Sxq = 2 * (a + b) * c
Trong đó:
Diện tích toàn phần của hình hộp chữ nhật là tổng diện tích của tất cả sáu mặt. Công thức tính diện tích toàn phần (Stp) như sau:
Stp = 2 * (a * b + a * c + b * c)
Hoặc có thể tính bằng công thức:
Stp = Sxq + 2 * (a * b)
Trong đó:
Ví dụ 1: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật đó.
Giải:
Diện tích xung quanh: Sxq = 2 * (5 + 3) * 4 = 64 cm2
Diện tích toàn phần: Stp = 2 * (5 * 3 + 5 * 4 + 3 * 4) = 94 cm2
Ví dụ 2: Một hình hộp chữ nhật có diện tích đáy là 20cm2 và diện tích xung quanh là 80cm2. Tính chiều cao của hình hộp chữ nhật đó.
Giải:
Chu vi đáy: P = Sxq / c => P = 80 / c
Ta có: a * b = 20 và 2 * (a + b) = P
Từ đó suy ra chiều cao c = 4cm
Diện tích toàn phần của hình hộp chữ nhật luôn lớn hơn diện tích xung quanh vì diện tích toàn phần bao gồm cả diện tích của hai mặt đáy.
Công thức tính diện tích hình hộp chữ nhật được ứng dụng rộng rãi trong thực tế, chẳng hạn như:
Để nắm vững kiến thức về công thức tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật, bạn nên luyện tập thêm với nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn rèn luyện kỹ năng và tự tin giải quyết các bài toán.
Việc hiểu và áp dụng đúng công thức tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật là rất quan trọng trong học Toán. Hy vọng với những kiến thức và ví dụ minh họa trên, bạn đã nắm vững các công thức này và có thể áp dụng chúng vào giải quyết các bài toán thực tế.