Chào mừng các em học sinh lớp 4 đến với bài học ôn hè về Lý thuyết Phân số và các phép tính với phân số. Bài học này được thiết kế để giúp các em nắm vững kiến thức cơ bản về phân số, từ đó tự tin giải các bài tập toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với hệ thống bài tập đa dạng, giúp các em ôn tập và củng cố kiến thức một cách hiệu quả.
Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó. Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
1. Phân số
Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.
Ví dụ:
\(\frac{4}{7}\) ; $\frac{1}{5}$ ; $\frac{{14}}{{13}}$ là những phân số.
2. Cách đọc, viết phân số
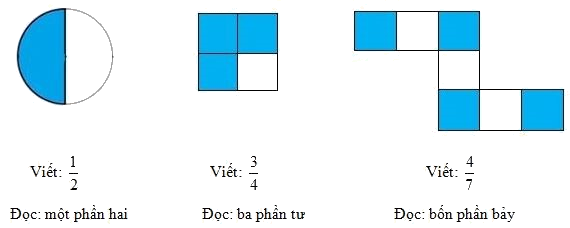
3. Phân số và phép chia số tự nhiên
Thương của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.
Ví dụ:
$3:4 = \frac{3}{4}$ ; $9:7 = \frac{9}{7}$
4. Phân số lớn hơn 1, bằng 1, nhỏ hơn 1
- Phân số có tử số lớn hơn mẫu số là phân số lớn hơn 1.
Ví dụ: $\frac{7}{6} > 1$ ; $\frac{{11}}{7} > 1$
- Phân số có tử số bé hơn mẫu số là phân số lớn hơn 1.
Ví dụ: $\frac{7}{9} < 1$ ; $\frac{{12}}{{13}} < 1$
- Phân số có tử số bằng mẫu số là phân số bằng 1.
Ví dụ: $\frac{8}{8} = 1$
5. Rút gọn phân số
Khi rút gọn phân số có thể làm như sau:
-Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
- Chia tử số và mẫu số cho số đó.
- Cứ làm như thế cho đến khi nhận được phân số tối giản.
Ví dụ: $\frac{9}{{12}} = \frac{{9:3}}{{12:3}} = \frac{3}{4}$
$\frac{{18}}{{27}} = \frac{{18:9}}{{27:9}} = \frac{2}{3}$
6. Phép cộng hai phân số
Muốn cộng hai phân số cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.
$\frac{a}{c} + \frac{b}{c} = \frac{{a + b}}{c}$
Ví dụ: $\frac{3}{7} + \frac{2}{7} = \frac{5}{7}$
Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
Ví dụ: $\frac{2}{3} + \frac{4}{5} = \frac{{10}}{{15}} + \frac{{12}}{{15}} = \frac{{22}}{{15}}$
7. Phép trừ hai phân số
Muốn trừ hai phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số.
$\frac{a}{c} - \frac{b}{c} = \frac{{a - b}}{c}$
Ví dụ: $\frac{7}{9} - \frac{2}{9} = \frac{5}{9}$
Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Ví dụ $\frac{5}{8} - \frac{1}{3} = \frac{{15}}{{24}} - \frac{8}{{24}} = \frac{7}{{24}}$
8. Phép nhân phân số
$\frac{a}{b} \times \frac{c}{d} = \frac{{a \times c}}{{b \times d}}$
Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Ví dụ: $\frac{5}{{12}} \times \frac{3}{{10}} = \frac{{5 \times 3}}{{12 \times 10}} = \frac{{15}}{{120}} = \frac{1}{8}$
Hoặc $\frac{5}{{12}} \times \frac{3}{{10}} = \frac{{5 \times 3}}{{12 \times 10}} = \frac{{\not 5 \times \not 3}}{{4 \times \not 3 \times \not 5 \times 2}} = \frac{1}{8}$
9. Phép chia phân số
Quy tắc: Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
$\frac{a}{b}:\frac{c}{d} = \frac{a}{b} \times \frac{d}{c} = \frac{{a \times d}}{{b \times c}}$
Ví dụ: $\frac{7}{{15}}:\frac{2}{3} = \frac{7}{{15}} \times \frac{3}{2} = \frac{{21}}{{30}} = \frac{7}{{10}}$
Phân số là một khái niệm quan trọng trong chương trình Toán học Tiểu học, đặc biệt là lớp 4. Việc nắm vững lý thuyết và các phép tính với phân số là nền tảng để học tốt các kiến thức toán học nâng cao hơn. Bài viết này sẽ cung cấp một cách đầy đủ và chi tiết về lý thuyết phân số và các phép tính cơ bản với phân số, giúp các em học sinh ôn tập và củng cố kiến thức trong kỳ nghỉ hè.
Một phân số được viết dưới dạng a/b, trong đó:
Phân số biểu thị một phần của một đơn vị hoặc một tập hợp. Ví dụ, phân số 1/2 biểu thị một nửa của một đơn vị.
Có ba loại phân số chính:
Để cộng hai phân số có cùng mẫu số, ta cộng các tử số lại với nhau và giữ nguyên mẫu số:
a/b + c/b = (a + c)/b
Ví dụ: 1/5 + 2/5 = 3/5
Để cộng hai phân số có mẫu số khác nhau, ta cần quy đồng mẫu số trước khi cộng.
Để trừ hai phân số có cùng mẫu số, ta trừ các tử số lại với nhau và giữ nguyên mẫu số:
a/b - c/b = (a - c)/b
Ví dụ: 4/7 - 1/7 = 3/7
Tương tự như phép cộng, để trừ hai phân số có mẫu số khác nhau, ta cần quy đồng mẫu số trước khi trừ.
Để nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu số với nhau:
a/b x c/d = (a x c) / (b x d)
Ví dụ: 2/3 x 1/4 = 2/12 = 1/6
Để chia hai phân số, ta nhân phân số bị chia với nghịch đảo của phân số chia:
a/b : c/d = a/b x d/c = (a x d) / (b x c)
Ví dụ: 3/4 : 1/2 = 3/4 x 2/1 = 6/4 = 3/2
Dưới đây là một số bài tập vận dụng để các em luyện tập:
Hy vọng bài viết này đã giúp các em học sinh lớp 4 ôn tập và củng cố kiến thức về Lý thuyết Phân số và các phép tính với phân số một cách hiệu quả. Chúc các em học tập tốt và có một kỳ nghỉ hè vui vẻ!