Bài viết này cung cấp bộ câu hỏi trắc nghiệm Bài 5: Hình chữ nhật chương trình Toán 8 Cánh diều, giúp học sinh ôn tập và củng cố kiến thức về hình chữ nhật. Các câu hỏi được thiết kế đa dạng, bao gồm các dạng bài tập cơ bản đến nâng cao, có đáp án và lời giải chi tiết.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán, mang đến những tài liệu học tập chất lượng và hiệu quả.
Hình chữ nhật có kích thước hai cạnh kề là \(5\,cm\) và \(12\,cm\). Độ dài đường chéo của hình chữ nhật đó là
Điền từ, cụm từ thích hợp vào chỗ (…) trong câu sau để được khẳng định đúng:
“Tứ giác có ... là hình chữ nhật.”
Hai đường chéo của hình chữ nhật có tính chất nào sau đây?
Chọn khẳng định đúng trong các khẳng định sau
Hình chữ nhật có mấy tâm đối xứng?
Hình bình hành cần có thêm điều kiện nào sau đây thì trở thành hình chữ nhật?
Cho hình chữ nhật \(ABCD\) có \(AB{\rm{ }} = {\rm{ }}6\;cm\) và đường chéo \(BD{\rm{ }} = {\rm{ }}10\;cm\). Tính độ dài cạnh \(BC\).
Hình bình hành \(ABCD\) là hình chữ nhật khi
Chọn câu sai. Tứ giác ABCD là hình chữ nhật khi:
Hãy chọn câu đúng. Cho ΔABC với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều kiện của ΔABC để tứ giác AEMF là hình chữ nhật.
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
Cho tam giác \(ABC\), đường cao \(AH\). \(I\) là trung điểm của \(AC\), \(E\) đối xứng với \(H\)qua \(I\). Tứ giác \(AHCE\) là hình gì?
Hình chữ nhật \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết \(\widehat {AOD} = {50^o}\), tính số đo \(\widehat {ABO}\).
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\), N, \(P\) lần lượt là trung điểm thuộc các cạnh \(AB\), AC, \(BC\) và \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\).Tứ giác \(AMPN\) là hình gì?
Cho hình chữ nhật \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\) và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\);\(EH\;\;{\rm{//}}\;\;BD\),\(FG\;\;{\rm{//}}\;\;BD\) Tứ giác \(EFGH\) là hình gì?
Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) . M và N lần lượt là các điểm của GC và GB và MN // BC; \(MN = \frac{1}{2}BC\); Tứ giác MNED là hình gì?
Cho hình thang vuông \(ABCD\) có \(\widehat A = \widehat D = {90^o}\) . Gọi \(M\) là trung điểm của \(AC\) và \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\) . Khẳng định nào sau đây sai
Cho tứ giác \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\)và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\), \(EH\;\;{\rm{//}}\;\;BD\), \(FG\;\;{\rm{//}}\;\;BD\). Tứ giác \(ABCD\) cần thêm điều kiện nào sau đây để tứ giác \(EFGH\) là hình chữ nhật?
Lời giải và đáp án
Hình chữ nhật có kích thước hai cạnh kề là \(5\,cm\) và \(12\,cm\). Độ dài đường chéo của hình chữ nhật đó là
Đáp án : B
Áp dụng định lý Pytago trong tam giác vuông, ta được độ dài đường chéo hình chữ nhật bằng
\(\sqrt {{5^2} + {{12}^2}} = \sqrt {169} = 13\;\left( {cm} \right)\)
Điền từ, cụm từ thích hợp vào chỗ (…) trong câu sau để được khẳng định đúng:
“Tứ giác có ... là hình chữ nhật.”
Đáp án : B
Hai đường chéo của hình chữ nhật có tính chất nào sau đây?
Đáp án : D
Chọn khẳng định đúng trong các khẳng định sau
Đáp án : B
Tứ giác có bốn cạnh bằng nhau có thể là hình thoi.
Tứ giác có bốn góc vuông là hình chữ nhật.
Tứ giác có hai góc vuông có thể là hình thang vuông.
Tứ giác có hai đường chéo bằng nhau có thể là hình thang cân.
Vậy đáp án B đúng.
Hình chữ nhật có mấy tâm đối xứng?
Đáp án : A
Hình bình hành cần có thêm điều kiện nào sau đây thì trở thành hình chữ nhật?
Đáp án : A
Cho hình chữ nhật \(ABCD\) có \(AB{\rm{ }} = {\rm{ }}6\;cm\) và đường chéo \(BD{\rm{ }} = {\rm{ }}10\;cm\). Tính độ dài cạnh \(BC\).
Đáp án : B
Hình chữ nhật \(ABCD\) có \(CD = AB = 6\;\;cm\).
Áp dụng định lý Pytago trong tam giác \(BCD\) , ta có:
\(BC = \sqrt {B{D^2} - C{D^2}} = \sqrt {{{10}^2} - {6^2}} = \sqrt {64} = 8\;\;\left( {cm} \right)\)
Hình bình hành \(ABCD\) là hình chữ nhật khi
Đáp án : B
Hình bình hành có một góc vuông là hình chữ nhật.
Chọn câu sai. Tứ giác ABCD là hình chữ nhật khi:
Đáp án : C
+ Ta thấy AB = CD = AD = BC thì ABCD chỉ có bốn cạnh bằng nhau nên ABCD chưa chắc là hình chữ nhật .
Nếu \(\widehat A = \widehat B = \widehat C = {90^o}\) thì tứ giác ABCD có ba góc vuông nên ABCD là hình chữ nhật (do dấu hiệu tứ giác có 3 góc vuông).
+ Nếu \(\widehat A = \widehat B = \widehat C = {90^o}\) và AB // CD thì tứ giác ABCD có AD // BC; AB // CD nên ABCD là hình bình hành, lại có Â = 900 nên ABCD là hình chữ nhật. (do dấu hiệu hình bình hành có một góc vuông)
+ Nếu AB // CD; AB = CD và AC = BD thì ABCD là hình bình hành (do có cặp cạnh đối AB; CD song song và bằng nhau), lại có hai đường chéo bằng nhau AC = BD nên ABCD là hình chữ nhật (do dấu hiệu hình bình hành có hai đường chéo bằng nhau).
Hãy chọn câu đúng. Cho ΔABC với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều kiện của ΔABC để tứ giác AEMF là hình chữ nhật.
Đáp án : A
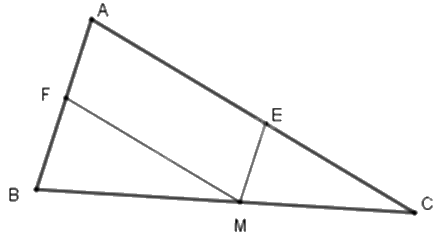
Từ giả thiết ta có ME // AF; MF // AE nên tứ giác AEMF là hình bình hành (dhnb).
Để hình bình hành AEMF là hình chữ nhật thì \(\widehat {{\rm{EAF}}} = {90^o}\) nên tam giác ABC vuông tại A.
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
Đáp án : C
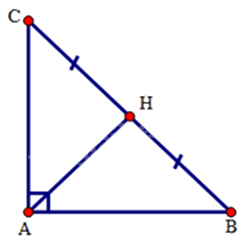
Áp dụng định lý Pytago cho tam giác ABC vuông tại A ta có:
BC2 = AC2 + AB2 hay BC2 = 62 + 82
⇒ BC2 = 100. Suy ra BC = 10 (cm)
Do AH là đường trung tuyến ứng với cạnh huyền BC nên
AH = BC : 2 = 10 : 2 = 5cm
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
Đáp án : A
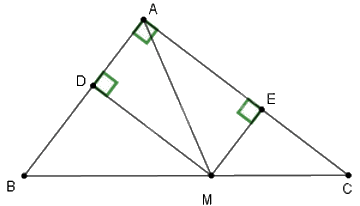
Xét tứ giác ADME có \(\widehat A = \widehat {A{\rm{D}}M} = \widehat {A{\rm{E}}M} = {90^o}\) nên ADME là hình chữ nhật.
Vì ADME là hình chữ nhật nên AM = DE (tính chất)
Để DE nhỏ nhất thì AM nhỏ nhất mà AM nhỏ nhất khi M là hình chiếu của A trên BC
Từ đó DE nhỏ nhất khi M là hình chiếu của A trên BC.
Cho tam giác \(ABC\), đường cao \(AH\). \(I\) là trung điểm của \(AC\), \(E\) đối xứng với \(H\)qua \(I\). Tứ giác \(AHCE\) là hình gì?
Đáp án : D
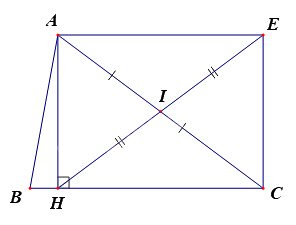
Tứ giác \(AHCE\) là hình bình hành vì \(IA = IC\), \(IH = IE\).
Mà \(\widehat H = {90^o}\)\( \Rightarrow AHCE\) là hình chữ nhật.
Hình bình hành có một góc vuông là hình chữ nhật
Hình chữ nhật \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết \(\widehat {AOD} = {50^o}\), tính số đo \(\widehat {ABO}\).
Đáp án : B
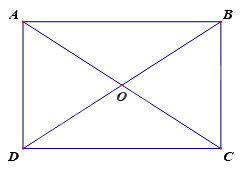
Ta có: \(\widehat {AOB} = {180^o} - \widehat {AOD} = {130^o}\) (hai góc kề bù)
Theo tính chất hình chữ nhật ta có \(OA = OB\) \( \Rightarrow \Delta OAB\) cân tại \(O\)
\( \Rightarrow \widehat {ABO} = \widehat {BAO} = \frac{{{{180}^o} - {{130}^o}}}{2} = {25^o}\).
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\), N, \(P\) lần lượt là trung điểm thuộc các cạnh \(AB\), AC, \(BC\) và \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\).Tứ giác \(AMPN\) là hình gì?
Đáp án : C
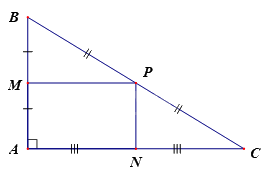
Xét tam giác ABC ta có: \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\)
Mà \(AN = \frac{{AC}}{2}\) \( \Rightarrow MP\;{\rm{ = }}\;AN\)
\( \Rightarrow \) Tứ giác \(AMPN\) là hình bình hành
Mà \(\widehat A = {90^o}\)\( \Rightarrow AMPN\) là hình chữ nhật.
Cho hình chữ nhật \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\) và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\);\(EH\;\;{\rm{//}}\;\;BD\),\(FG\;\;{\rm{//}}\;\;BD\) Tứ giác \(EFGH\) là hình gì?
Đáp án : D
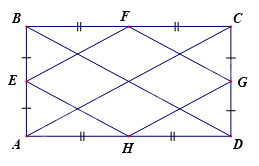
Tứ giác \(EFGH\) là hình bình hành vì
+ \(EF\;\;{\rm{//}}\;\;GH\) (\(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\))
+ \(EH\;\;{\rm{//}}\;\;FG\) (\(EH\;\;{\rm{//}}\;\;BD\),\(FG\;\;{\rm{//}}\;\;BD\))
Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
Đáp án : D
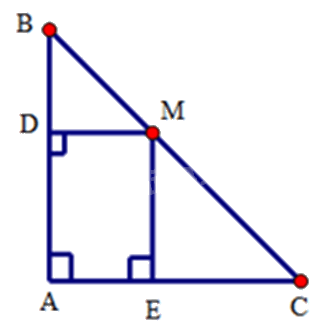
+ Xét tứ giác ADME có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\) nên ADME là hình chữ nhật
+ Xét tam giác DMB có \(\widehat B = {45^o}\) (do tam giác ABC vuông cân) nên tam giác BDM vuông cân tại D. Do đó DM = BD
+ Do ADME là hình chữ nhật nên chu vi ADME là:
(AD + DM).2 = (AD + BD).2 = 6.2 = 12 cm
Vậy chu vi ADME là 12cm
Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) . M và N lần lượt là các điểm của GC và GB và MN // BC; \(MN = \frac{1}{2}BC\); Tứ giác MNED là hình gì?
Đáp án : B
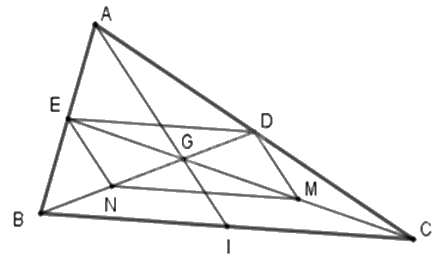
Xét tam giác ABC : ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) (1)
+ Xét tam giác GBC có : MN // BC; \(MN = \frac{1}{2}BC\) (2)
Từ (1), (2) ⇒ MN // ED, MN = ED nên tứ giác MNED là hình bình hành (dấu hiệu nhận biết)
Cho hình thang vuông \(ABCD\) có \(\widehat A = \widehat D = {90^o}\) . Gọi \(M\) là trung điểm của \(AC\) và \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\) . Khẳng định nào sau đây sai
Đáp án : D
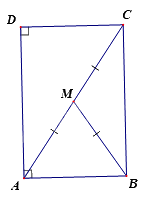
Xét \(\Delta ABC\) có \(BM\) là đường trung tuyến ứng với cạnh \(AC\) mà \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\)\( \Rightarrow \Delta ABC\) vuông tại \(B\)
Tứ giác \(ABCD\) có \(\widehat A = \widehat D = \widehat B = {90^o}\)\( \Rightarrow \) Tứ giác \(ABCD\) là hình chữ nhật.
Suy ra: \(AC = BD\) và \(M\) là trung điểm của \(BD\)
Vậy D sai.
Cho tứ giác \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\)và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\), \(EH\;\;{\rm{//}}\;\;BD\), \(FG\;\;{\rm{//}}\;\;BD\). Tứ giác \(ABCD\) cần thêm điều kiện nào sau đây để tứ giác \(EFGH\) là hình chữ nhật?
Đáp án : B
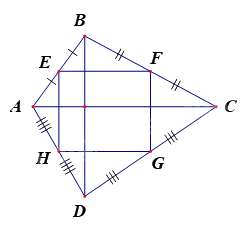
Tứ giác \(EFGH\) là hình bình hành vì
+ \(EF\;\;{\rm{//}}\;\;GH\) (\(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\))
+ \(EH\;\;{\rm{//}}\;\;FG\) (\(EH\;\;{\rm{//}}\;\;BD\), \(FG\;\;{\rm{//}}\;\;BD\))
Để hình bình hành \(EFGH\) là hình chữ nhật cần thêm điều kiện \(\widehat E = {90^o}\)
\( \Rightarrow EF \bot EH\) \( \Leftrightarrow AC \bot BD\)
Hình chữ nhật có kích thước hai cạnh kề là \(5\,cm\) và \(12\,cm\). Độ dài đường chéo của hình chữ nhật đó là
Điền từ, cụm từ thích hợp vào chỗ (…) trong câu sau để được khẳng định đúng:
“Tứ giác có ... là hình chữ nhật.”
Hai đường chéo của hình chữ nhật có tính chất nào sau đây?
Chọn khẳng định đúng trong các khẳng định sau
Hình chữ nhật có mấy tâm đối xứng?
Hình bình hành cần có thêm điều kiện nào sau đây thì trở thành hình chữ nhật?
Cho hình chữ nhật \(ABCD\) có \(AB{\rm{ }} = {\rm{ }}6\;cm\) và đường chéo \(BD{\rm{ }} = {\rm{ }}10\;cm\). Tính độ dài cạnh \(BC\).
Hình bình hành \(ABCD\) là hình chữ nhật khi
Chọn câu sai. Tứ giác ABCD là hình chữ nhật khi:
Hãy chọn câu đúng. Cho ΔABC với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều kiện của ΔABC để tứ giác AEMF là hình chữ nhật.
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
Cho tam giác \(ABC\), đường cao \(AH\). \(I\) là trung điểm của \(AC\), \(E\) đối xứng với \(H\)qua \(I\). Tứ giác \(AHCE\) là hình gì?
Hình chữ nhật \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết \(\widehat {AOD} = {50^o}\), tính số đo \(\widehat {ABO}\).
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\), N, \(P\) lần lượt là trung điểm thuộc các cạnh \(AB\), AC, \(BC\) và \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\).Tứ giác \(AMPN\) là hình gì?
Cho hình chữ nhật \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\) và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\);\(EH\;\;{\rm{//}}\;\;BD\),\(FG\;\;{\rm{//}}\;\;BD\) Tứ giác \(EFGH\) là hình gì?
Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) . M và N lần lượt là các điểm của GC và GB và MN // BC; \(MN = \frac{1}{2}BC\); Tứ giác MNED là hình gì?
Cho hình thang vuông \(ABCD\) có \(\widehat A = \widehat D = {90^o}\) . Gọi \(M\) là trung điểm của \(AC\) và \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\) . Khẳng định nào sau đây sai
Cho tứ giác \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\)và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\), \(EH\;\;{\rm{//}}\;\;BD\), \(FG\;\;{\rm{//}}\;\;BD\). Tứ giác \(ABCD\) cần thêm điều kiện nào sau đây để tứ giác \(EFGH\) là hình chữ nhật?
Hình chữ nhật có kích thước hai cạnh kề là \(5\,cm\) và \(12\,cm\). Độ dài đường chéo của hình chữ nhật đó là
Đáp án : B
Áp dụng định lý Pytago trong tam giác vuông, ta được độ dài đường chéo hình chữ nhật bằng
\(\sqrt {{5^2} + {{12}^2}} = \sqrt {169} = 13\;\left( {cm} \right)\)
Điền từ, cụm từ thích hợp vào chỗ (…) trong câu sau để được khẳng định đúng:
“Tứ giác có ... là hình chữ nhật.”
Đáp án : B
Hai đường chéo của hình chữ nhật có tính chất nào sau đây?
Đáp án : D
Chọn khẳng định đúng trong các khẳng định sau
Đáp án : B
Tứ giác có bốn cạnh bằng nhau có thể là hình thoi.
Tứ giác có bốn góc vuông là hình chữ nhật.
Tứ giác có hai góc vuông có thể là hình thang vuông.
Tứ giác có hai đường chéo bằng nhau có thể là hình thang cân.
Vậy đáp án B đúng.
Hình chữ nhật có mấy tâm đối xứng?
Đáp án : A
Hình bình hành cần có thêm điều kiện nào sau đây thì trở thành hình chữ nhật?
Đáp án : A
Cho hình chữ nhật \(ABCD\) có \(AB{\rm{ }} = {\rm{ }}6\;cm\) và đường chéo \(BD{\rm{ }} = {\rm{ }}10\;cm\). Tính độ dài cạnh \(BC\).
Đáp án : B
Hình chữ nhật \(ABCD\) có \(CD = AB = 6\;\;cm\).
Áp dụng định lý Pytago trong tam giác \(BCD\) , ta có:
\(BC = \sqrt {B{D^2} - C{D^2}} = \sqrt {{{10}^2} - {6^2}} = \sqrt {64} = 8\;\;\left( {cm} \right)\)
Hình bình hành \(ABCD\) là hình chữ nhật khi
Đáp án : B
Hình bình hành có một góc vuông là hình chữ nhật.
Chọn câu sai. Tứ giác ABCD là hình chữ nhật khi:
Đáp án : C
+ Ta thấy AB = CD = AD = BC thì ABCD chỉ có bốn cạnh bằng nhau nên ABCD chưa chắc là hình chữ nhật .
Nếu \(\widehat A = \widehat B = \widehat C = {90^o}\) thì tứ giác ABCD có ba góc vuông nên ABCD là hình chữ nhật (do dấu hiệu tứ giác có 3 góc vuông).
+ Nếu \(\widehat A = \widehat B = \widehat C = {90^o}\) và AB // CD thì tứ giác ABCD có AD // BC; AB // CD nên ABCD là hình bình hành, lại có Â = 900 nên ABCD là hình chữ nhật. (do dấu hiệu hình bình hành có một góc vuông)
+ Nếu AB // CD; AB = CD và AC = BD thì ABCD là hình bình hành (do có cặp cạnh đối AB; CD song song và bằng nhau), lại có hai đường chéo bằng nhau AC = BD nên ABCD là hình chữ nhật (do dấu hiệu hình bình hành có hai đường chéo bằng nhau).
Hãy chọn câu đúng. Cho ΔABC với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều kiện của ΔABC để tứ giác AEMF là hình chữ nhật.
Đáp án : A

Từ giả thiết ta có ME // AF; MF // AE nên tứ giác AEMF là hình bình hành (dhnb).
Để hình bình hành AEMF là hình chữ nhật thì \(\widehat {{\rm{EAF}}} = {90^o}\) nên tam giác ABC vuông tại A.
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
Đáp án : C

Áp dụng định lý Pytago cho tam giác ABC vuông tại A ta có:
BC2 = AC2 + AB2 hay BC2 = 62 + 82
⇒ BC2 = 100. Suy ra BC = 10 (cm)
Do AH là đường trung tuyến ứng với cạnh huyền BC nên
AH = BC : 2 = 10 : 2 = 5cm
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
Đáp án : A

Xét tứ giác ADME có \(\widehat A = \widehat {A{\rm{D}}M} = \widehat {A{\rm{E}}M} = {90^o}\) nên ADME là hình chữ nhật.
Vì ADME là hình chữ nhật nên AM = DE (tính chất)
Để DE nhỏ nhất thì AM nhỏ nhất mà AM nhỏ nhất khi M là hình chiếu của A trên BC
Từ đó DE nhỏ nhất khi M là hình chiếu của A trên BC.
Cho tam giác \(ABC\), đường cao \(AH\). \(I\) là trung điểm của \(AC\), \(E\) đối xứng với \(H\)qua \(I\). Tứ giác \(AHCE\) là hình gì?
Đáp án : D

Tứ giác \(AHCE\) là hình bình hành vì \(IA = IC\), \(IH = IE\).
Mà \(\widehat H = {90^o}\)\( \Rightarrow AHCE\) là hình chữ nhật.
Hình bình hành có một góc vuông là hình chữ nhật
Hình chữ nhật \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết \(\widehat {AOD} = {50^o}\), tính số đo \(\widehat {ABO}\).
Đáp án : B

Ta có: \(\widehat {AOB} = {180^o} - \widehat {AOD} = {130^o}\) (hai góc kề bù)
Theo tính chất hình chữ nhật ta có \(OA = OB\) \( \Rightarrow \Delta OAB\) cân tại \(O\)
\( \Rightarrow \widehat {ABO} = \widehat {BAO} = \frac{{{{180}^o} - {{130}^o}}}{2} = {25^o}\).
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\), N, \(P\) lần lượt là trung điểm thuộc các cạnh \(AB\), AC, \(BC\) và \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\).Tứ giác \(AMPN\) là hình gì?
Đáp án : C

Xét tam giác ABC ta có: \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\)
Mà \(AN = \frac{{AC}}{2}\) \( \Rightarrow MP\;{\rm{ = }}\;AN\)
\( \Rightarrow \) Tứ giác \(AMPN\) là hình bình hành
Mà \(\widehat A = {90^o}\)\( \Rightarrow AMPN\) là hình chữ nhật.
Cho hình chữ nhật \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\) và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\);\(EH\;\;{\rm{//}}\;\;BD\),\(FG\;\;{\rm{//}}\;\;BD\) Tứ giác \(EFGH\) là hình gì?
Đáp án : D

Tứ giác \(EFGH\) là hình bình hành vì
+ \(EF\;\;{\rm{//}}\;\;GH\) (\(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\))
+ \(EH\;\;{\rm{//}}\;\;FG\) (\(EH\;\;{\rm{//}}\;\;BD\),\(FG\;\;{\rm{//}}\;\;BD\))
Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
Đáp án : D

+ Xét tứ giác ADME có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\) nên ADME là hình chữ nhật
+ Xét tam giác DMB có \(\widehat B = {45^o}\) (do tam giác ABC vuông cân) nên tam giác BDM vuông cân tại D. Do đó DM = BD
+ Do ADME là hình chữ nhật nên chu vi ADME là:
(AD + DM).2 = (AD + BD).2 = 6.2 = 12 cm
Vậy chu vi ADME là 12cm
Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) . M và N lần lượt là các điểm của GC và GB và MN // BC; \(MN = \frac{1}{2}BC\); Tứ giác MNED là hình gì?
Đáp án : B

Xét tam giác ABC : ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) (1)
+ Xét tam giác GBC có : MN // BC; \(MN = \frac{1}{2}BC\) (2)
Từ (1), (2) ⇒ MN // ED, MN = ED nên tứ giác MNED là hình bình hành (dấu hiệu nhận biết)
Cho hình thang vuông \(ABCD\) có \(\widehat A = \widehat D = {90^o}\) . Gọi \(M\) là trung điểm của \(AC\) và \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\) . Khẳng định nào sau đây sai
Đáp án : D

Xét \(\Delta ABC\) có \(BM\) là đường trung tuyến ứng với cạnh \(AC\) mà \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\)\( \Rightarrow \Delta ABC\) vuông tại \(B\)
Tứ giác \(ABCD\) có \(\widehat A = \widehat D = \widehat B = {90^o}\)\( \Rightarrow \) Tứ giác \(ABCD\) là hình chữ nhật.
Suy ra: \(AC = BD\) và \(M\) là trung điểm của \(BD\)
Vậy D sai.
Cho tứ giác \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\)và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\), \(EH\;\;{\rm{//}}\;\;BD\), \(FG\;\;{\rm{//}}\;\;BD\). Tứ giác \(ABCD\) cần thêm điều kiện nào sau đây để tứ giác \(EFGH\) là hình chữ nhật?
Đáp án : B

Tứ giác \(EFGH\) là hình bình hành vì
+ \(EF\;\;{\rm{//}}\;\;GH\) (\(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\))
+ \(EH\;\;{\rm{//}}\;\;FG\) (\(EH\;\;{\rm{//}}\;\;BD\), \(FG\;\;{\rm{//}}\;\;BD\))
Để hình bình hành \(EFGH\) là hình chữ nhật cần thêm điều kiện \(\widehat E = {90^o}\)
\( \Rightarrow EF \bot EH\) \( \Leftrightarrow AC \bot BD\)
Bài 5: Hình chữ nhật trong chương trình Toán 8 Cánh diều là một phần quan trọng, đặt nền móng cho việc học các kiến thức hình học phức tạp hơn. Hình chữ nhật là một tứ giác đặc biệt, có bốn góc vuông và các cạnh đối song song, bằng nhau. Việc nắm vững các tính chất, định lý liên quan đến hình chữ nhật là điều kiện cần thiết để giải quyết các bài toán hình học một cách hiệu quả.
Câu 1: Tứ giác ABCD có góc A = góc B = góc C = 90 độ. ABCD là hình gì?
A. Hình vuông
B. Hình chữ nhật
C. Hình thoi
D. Hình bình hành
Đáp án: B. Vì tứ giác có ba góc vuông nên là hình chữ nhật.
Câu 2: Hình chữ nhật ABCD có AB = 6cm, BC = 8cm. Độ dài đường chéo AC là bao nhiêu?
A. 10cm
B. 12cm
C. 14cm
D. 16cm
Đáp án: A. Áp dụng định lý Pitago trong tam giác vuông ABC, ta có AC2 = AB2 + BC2 = 62 + 82 = 36 + 64 = 100. Suy ra AC = √100 = 10cm.
Để nâng cao khả năng giải quyết các bài tập trắc nghiệm về hình chữ nhật, bạn nên luyện tập thêm với nhiều đề bài khác nhau. Giaitoan.edu.vn cung cấp một kho đề thi phong phú, đa dạng, đáp ứng nhu cầu học tập của mọi đối tượng học sinh.
Trắc nghiệm Bài 5: Hình chữ nhật Toán 8 Cánh diều là một phần quan trọng trong chương trình học. Việc nắm vững kiến thức và luyện tập thường xuyên sẽ giúp học sinh đạt kết quả tốt trong các bài kiểm tra và thi cử. Chúc các em học tập tốt!