Bài 9: Hình đồng dạng trong chương trình Toán 8 Cánh diều là một phần quan trọng giúp học sinh hiểu rõ về tỉ lệ thức, tam giác đồng dạng và ứng dụng của chúng trong giải toán. Trắc nghiệm này được thiết kế để giúp các em ôn tập và đánh giá kiến thức đã học một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp bộ đề trắc nghiệm đa dạng, bao gồm các câu hỏi từ dễ đến khó, kèm theo đáp án chi tiết và lời giải thích rõ ràng. Hãy cùng luyện tập để tự tin hơn trong các bài kiểm tra và thi cử!
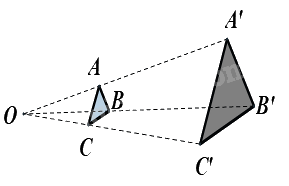
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3.\) Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:
Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) với tâm phối cảnh là:
Chọn đáp án đúng nhất
Cho hình chữ nhật ba hình chữ nhật ABCD, A’B’C’D’, A”B”C”D” sao cho:
+ Hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh
+ Hình A”B”C”D” bằng hình A’B’C’D’
Chọn đáp án đúng
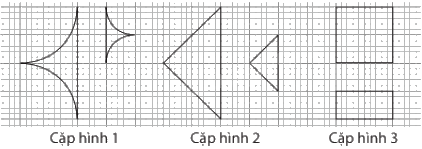
Trong những cặp hình cho ở hình vẽ dưới đây, có mấy cặp hình là hình đồng dạng?
Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA và OB.
Chọn đáp án đúng.
Cho các hình vẽ sau:
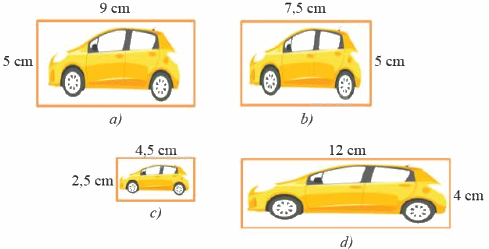
Hình nào đồng dạng với hình a?
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3.\) Nếu độ dài cạnh của hình vuông ABCD là 9cm thì độ dài cạnh của hình vuông A’B’C’D’ là:
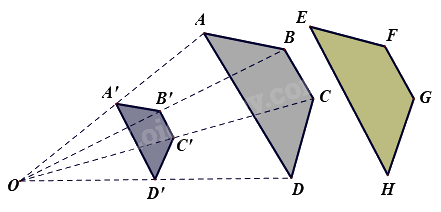
Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.
Cho các khẳng định sau:
+ Hình thang ABCD và EFGH bằng nhau
+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau
+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’
Có bao nhiêu khẳng định đúng?
Cho tam giác ABC có AB = 4, BC = 7, CA = 6. Cho O, I là điểm phân biệt.
+ Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\)
+ Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\).
Chọn đáp án đúng
Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Qua M vẽ đường thẳng vuông góc với AB cắt AB tại H.
Chọn đáp án đúng
Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh là 10cm và 8cm.
Chọn câu trả lời đúng nhất
Tam giác ABC có chu vi bằng 18cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\). Chu vi tam giác A’B’C’ bằng:
Hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD theo tỉ số đồng dạng k. Biết rằng diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\), diện tích hình vuông ABCD là \(36c{m^2}.\) Khi đó, tỉ số đồng dạng k bằng:
Cho hình tròn H có diện tích bằng \(113,04c{m^2}\). Hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\). Khi đó, diện tích của hình tròn H’ bằng:
Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\). Biết rằng diện tích tam giác ABC bằng \(48c{m^2}.\) Diện tích tam giác AMN bằng:
Cho tam giác ABC. Trên cạnh BC lấy điểm K sao cho \(CK = \frac{2}{3}BC.\) Tìm trên AB điểm H sao cho cạnh HK là hình đồng dạng phối cảnh của cạnh AC (với tâm đồng dạng phối cảnh là điểm B)
: Cho hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 6cm,BC = 8cm,A'B' = 12cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ là:
Cho tam giác ABC có \(AB = 3cm,BC = 4cm,AC = 5cm.\) Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích tam giác A”B”C” bằng \(96c{m^2}\).
Chọn đáp án đúng
Cho hình chữ nhật ABCD có \(AB = \frac{3}{4}BC.\) Hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD theo tỉ số đồng dạng 2. Biết rằng \(A'C' = 10cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ bằng:
Lời giải và đáp án
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3.\) Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:
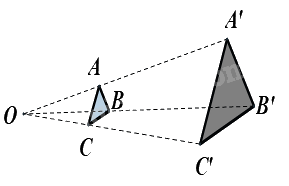
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3\) nên tam giác A’B’C’ và tam giác ABC là đồng dạng phối cảnh với tỉ số vị tự là 3.
Do đó tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là \(\frac{1}{3}\).
Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) với tâm phối cảnh là:
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Chọn đáp án đúng nhất
Đáp án : C
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
+ Hai hình H, H’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Do đó, cả A và B đều đúng
Cho hình chữ nhật ba hình chữ nhật ABCD, A’B’C’D’, A”B”C”D” sao cho:
+ Hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh
+ Hình A”B”C”D” bằng hình A’B’C’D’
Chọn đáp án đúng
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng
Vì hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh và hình A”B”C”D” bằng hình A’B’C’D’ nên
+ Hình A’B’C’D’ đồng dạng với hình ABCD
+ Hình A”B”C”D” đồng dạng với hình ABCD
Do đó, cả A, B đều đúng
Trong những cặp hình cho ở hình vẽ dưới đây, có mấy cặp hình là hình đồng dạng?
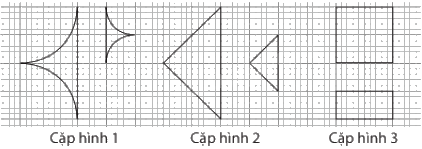
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Các cặp hình đồng dạng là: Cặp hình 1 và cặp hình 2.
Vậy có 2 cặp hình đồng dạng.
Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA và OB.
Chọn đáp án đúng.
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.
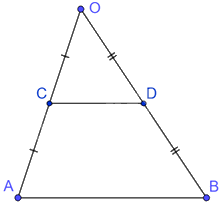
Vì C là trung điểm của OA nên \(OC = \frac{1}{2}OA\)
Vì D là trung điểm của OB nên \(OD = \frac{1}{2}OB\)
Mà O là giao điểm của AC và BD nên cạnh CD là hình đồng dạng phối cảnh của cạnh AB với tỉ số đồng dạng \(k = \frac{1}{2}\), tâm phối cảnh là điểm O.
Do đó, cạnh CD là hình đồng dạng của cạnh AB với tỉ số \(k = \frac{1}{2}\)
Suy ra, cả A, B đều đúng.
Cho các hình vẽ sau:
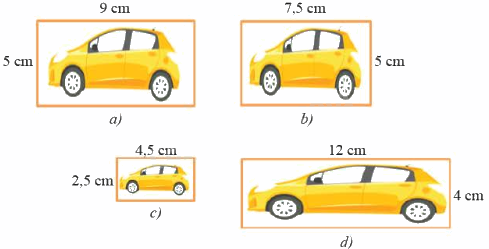
Hình nào đồng dạng với hình a?
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì \(\frac{5}{5} \ne \frac{9}{{7,5}}\) nên hình a và hình b không phải là hai hình đồng dạng
Vì \(\frac{5}{{2,5}} = \frac{9}{{4,5}}\) nên hình a và hình c là hai hình đồng dạng với nhau
Vì \(\frac{{12}}{9} \ne \frac{4}{5}\) nên hình a và hình d không phải là hai hình đồng dạng
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng là: \(\frac{6}{3} = 2\)
Hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3.\) Nếu độ dài cạnh của hình vuông ABCD là 9cm thì độ dài cạnh của hình vuông A’B’C’D’ là:
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.
Vì hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3\) nên cạnh của hình vuông A’B’C’D’ gấp 3 lần cạnh của hình vuông ABCD. Do đó, cạnh của hình vuông A’B’C’D’ là: \(9.3 = 27\left( {cm} \right)\)
Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.
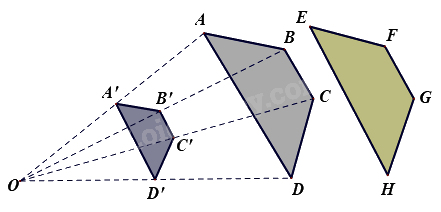
Cho các khẳng định sau:
+ Hình thang ABCD và EFGH bằng nhau
+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau
+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’
Có bao nhiêu khẳng định đúng?
Đáp án : D
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Hình thang ABCD và EFGH bằng nhau.
Vì các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD nên \(OA = 2OA',OB = 2OB',OC = 2OC',OD = 2OD'\).
Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’.
Do đó, hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau.
Vậy cả 3 khẳng định trên đều đúng
Cho tam giác ABC có AB = 4, BC = 7, CA = 6. Cho O, I là điểm phân biệt.
+ Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\)
+ Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\).
Chọn đáp án đúng
Đáp án : A
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh nên \(\frac{OA'}{OA}=\frac{OB'}{OB}=\frac{OC'}{OC}\) suy ra \( \Delta A'B'C'\backsim \Delta ABC\), do đó \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=3\)
suy ra \(A'B'=12;B'C'=21;C'A'=18\)
Vì tam giác A”B”C” là hình đồng dạng phối cảnh của tam giác ABC với I là tâm đồng dạng phối cảnh nên \(\frac{IA''}{IA}=\frac{IB''}{IB}=\frac{IC''}{IC}\) suy ra \( \Delta A''B''C''\backsim \Delta ABC\), do đó \(\frac{A''B''}{AB}=\frac{B''C''}{BC}=\frac{C''A''}{CA}=3\)
suy ra \(A''B''=12;B''C''=21;C''A''=18\)
Do đó, \(A'B'=A''B''=21,B'C'=B''C''=21,C'A'=C''A''=18\)
suy ra \(\frac{A''B''}{A'B'}=\frac{C''B''}{C'B'}=\frac{A''C''}{A'C'}=1\)
Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Qua M vẽ đường thẳng vuông góc với AB cắt AB tại H.
Chọn đáp án đúng
Đáp án : A
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H ’bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
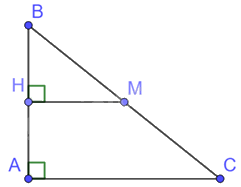
Ta có: \(HM \bot AB,AC \bot AB\) nên HM//AC
Tam giác ABC có: M là trung điểm của BC, HM//AC nên H là trung điểm của AB.
Do đó, \(\frac{{BH}}{{BA}} = \frac{1}{2}\)
Lại có: Mà là trung điểm của BC nên \(\frac{{BM}}{{BC}} = \frac{1}{2}\)
Suy ra: \(\frac{{BH}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{2}\)
Mà đường thẳng AH và MC cùng đi qua điểm B.
Do đó, HM là hình đồng dạng phối cảnh của cạnh AC, tâm B, tỉ số \(\frac{1}{2}\)
Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh là 10cm và 8cm.
Chọn câu trả lời đúng nhất
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
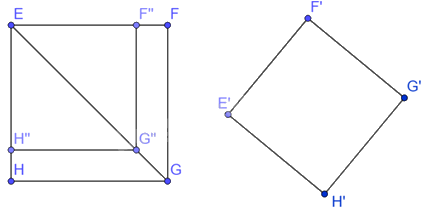
Trên các đoạn thẳng EF, EG, EH, ta lần lượt lấy các điểm F”, G”, H” sao cho \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}.\) Theo định lý Thalès đảo ta có: F”G”//FG, G”H”//GH.
Mà \(\widehat{F''EH''}={{90}^{0}}\) nên tứ giác EF”G”H” là hình chữ nhật.
Mặt khác, ta có: \(\frac{EF''}{EF}=\frac{F''G''}{FG}=\frac{G''H''}{GH}=\frac{H''E}{HE}=\frac{4}{5}\) (hệ quả định lí Thalès)
Suy ra \(EF''=F''G''=G''H''=H''E=8cm\) .
Do đó, tứ giác EF”G”H” là hình vuông có độ dài cạnh bằng 8cm.
Suy ra, hai hình vuông EF”G”H” và E’F’G’H’ bằng nhau
Vì \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}\) nên hình vuông EF”G”H” đồng dạng phối cảnh với hình vuông EFGH hay hình vuông E’F’G’H’ đồng dạng phối cảnh với hình vuông EFGH.
Vậy hình vuông E’F’G’H’ đồng dạng với hình vuông EFGH.
Tam giác ABC có chu vi bằng 18cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\). Chu vi tam giác A’B’C’ bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Tam giác ABC có chu vi bằng 18cm nên \(AB + BC + CA = 18\)
Chu vi tam giác A’B’C’ là: \(P' = A'B' + A'C' + B'C'\)
Vì tam A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\) nên \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{3}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{{A'B' + A'C' + B'C'}}{{AB + AC + BC}} = \frac{{P'}}{{18}} = \frac{1}{3}\)
\( \Rightarrow P' = 18:3 = 6\left( {cm} \right)\)
Vậy chu vi tam giác A’B’C’ bằng 6cm
Hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD theo tỉ số đồng dạng k. Biết rằng diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\), diện tích hình vuông ABCD là \(36c{m^2}.\) Khi đó, tỉ số đồng dạng k bằng:
Đáp án : A
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H ’bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\) nên ta có: \(A'B{'^2} = 64 \Rightarrow A'B' = 8cm\)
Vì diện tích hình vuông ABCD là \(36c{m^2}\) nên ta có: \(A{B^2} = 36 \Rightarrow AB = 6cm\)
Vì hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD tỉ số đồng dạng k nên:
\(k = \frac{{A'B'}}{{AB}} = \frac{8}{6} = \frac{4}{3}\)
Vậy tỉ số đồng dạng là \(\frac{4}{3}\)
Cho hình tròn H có diện tích bằng \(113,04c{m^2}\). Hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\). Khi đó, diện tích của hình tròn H’ bằng:
Đáp án : C
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình tròn H có diện tích bằng \(113,04c{m^2}\) nên bán kính của hình tròn là: \({R^2} = \frac{{113,04}}{{3,14}} = 36 \Rightarrow R = 6cm\)
Vì hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\) nên bán kính hình tròn H’ là: \(R' = \frac{R}{2} = 3\left( {cm} \right)\)
Diện tích hình tròn H’ là: \({3^2}.3,14 = 28,26c{m^2}\)
Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\). Biết rằng diện tích tam giác ABC bằng \(48c{m^2}.\) Diện tích tam giác AMN bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
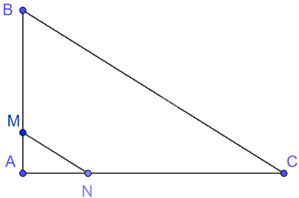
Vì đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{4} \Rightarrow AB = 4AM,AC = 4AN\)
Diện tích tam giác AMN vuông tại A là: \({S_{AMN}} = \frac{1}{2}AM.AN\)
Vì tam giác ABC vuông tại A nên diện tích tam giác ABC là:
\(\frac{1}{2}AB.AC = 48 \Rightarrow \frac{1}{2}.4AM.4AN = 48 \Rightarrow \frac{1}{2}AM.AN = 3\left( {c{m^2}} \right)\)
Do đó, diện tích tam giác AMN bằng \(3c{m^2}\).
Cho tam giác ABC. Trên cạnh BC lấy điểm K sao cho \(CK = \frac{2}{3}BC.\) Tìm trên AB điểm H sao cho cạnh HK là hình đồng dạng phối cảnh của cạnh AC (với tâm đồng dạng phối cảnh là điểm B)
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
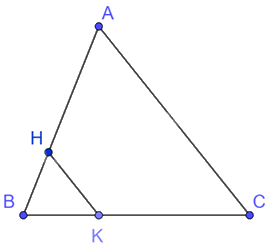
Vì H thuộc AB và HK là hình đồng dạng phối cảnh của cạnh AC, với tâm đồng dạng phối cảnh là điểm B nên \(\frac{{HK}}{{AC}} = \frac{{BK}}{{BC}} = \frac{{BH}}{{BA}}\)
Mà \(CK = \frac{2}{3}BC \Rightarrow \frac{{BK}}{{BC}} = \frac{1}{3} \Rightarrow \frac{{BH}}{{BA}} = \frac{{KH}}{{AC}} = \frac{1}{3}\)
Do đó, điểm H cần tìm thuộc đoạn thẳng AB sao cho \(BH = \frac{1}{3}AB\).
: Cho hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 6cm,BC = 8cm,A'B' = 12cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ là:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k nên \(k = \frac{{A'B'}}{{AB}} = \frac{{12}}{6} = 2\)
Ta có: \(\frac{{B'C'}}{{BC}} = 2 \Rightarrow B'C' = 8.2 = 16\left( {cm} \right)\)
Diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 12.16 = 192\left( {c{m^2}} \right)\)
Cho tam giác ABC có \(AB = 3cm,BC = 4cm,AC = 5cm.\) Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích tam giác A”B”C” bằng \(96c{m^2}\).
Chọn đáp án đúng
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2 nên \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=2\)
\(\Rightarrow A'B'=6cm,B'C'=8cm,A'C'=10cm\)
Vì \(A'C{{'}^{2}}=A'B{{'}^{2}}+B'C{{'}^{2}}\left( {{10}^{2}}={{8}^{2}}+{{6}^{2}} \right)\) nên tam giác A’B’C’ vuông tại B’
Vì tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x nên \(\Delta A''B''C''\backsim \Delta A'B'C'\)
Do đó, \(\widehat{A''B''C''}=\widehat{A'B'C'}=90\) và \(\frac{A''B''}{A'B'}=\frac{A''C''}{A'C'}=\frac{B''C''}{B'C'}=x\Rightarrow A''B''=6x,A''C''=10x,B''C''=8x\)
Vì tam giác A”B”C” vuông tại B” nên diện tích tam giác A”B”C” là:
\({{S}_{A''B''C''}}=\frac{1}{2}B''A''.B''C''\Rightarrow \frac{1}{2}.6x.8x=96\Rightarrow {{x}^{2}}=4\Rightarrow x=2\) (do \(x>0\))
Cho hình chữ nhật ABCD có \(AB = \frac{3}{4}BC.\) Hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD theo tỉ số đồng dạng 2. Biết rằng \(A'C' = 10cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ bằng:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD có tỉ số đồng dạng 2 nên \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = 2\)
Mà \(AB = \frac{3}{4}BC \Rightarrow A'B' = \frac{3}{4}B'C'.\)
Vì A’B’C’D’ là hình chữ nhật nên \(\widehat {A'B'C'} = {90^0}\)
Do đó, tam giác A’B’C’ vuông tại B’. Áp dụng định lý Pytago vào tam giác A’B’C’ vuông tại B’ ta có: \(A'C{'^2} = A'B{'^2} + B'C{'^2}\) (1)
Thay \(A'B' = \frac{3}{4}B'C'\) vào (1) ta có:
\({\left( {\frac{3}{4}B'C'} \right)^2} + B'C{'^2} = {10^2}\)
\(\frac{{25}}{{16}}B'C{'^2} = 100\)
\(B'C{'^2} = 64\) nên \(B'C' = 8cm\)
Do đó, \(A'B' = 8.\frac{3}{4} = 6\left( {cm} \right)\)
Vậy diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 6.8 = 48\left( {c{m^2}} \right)\)
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3.\) Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:

Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) với tâm phối cảnh là:
Chọn đáp án đúng nhất
Cho hình chữ nhật ba hình chữ nhật ABCD, A’B’C’D’, A”B”C”D” sao cho:
+ Hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh
+ Hình A”B”C”D” bằng hình A’B’C’D’
Chọn đáp án đúng
Trong những cặp hình cho ở hình vẽ dưới đây, có mấy cặp hình là hình đồng dạng?

Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA và OB.
Chọn đáp án đúng.
Cho các hình vẽ sau:

Hình nào đồng dạng với hình a?
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3.\) Nếu độ dài cạnh của hình vuông ABCD là 9cm thì độ dài cạnh của hình vuông A’B’C’D’ là:
Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.

Cho các khẳng định sau:
+ Hình thang ABCD và EFGH bằng nhau
+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau
+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’
Có bao nhiêu khẳng định đúng?
Cho tam giác ABC có AB = 4, BC = 7, CA = 6. Cho O, I là điểm phân biệt.
+ Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\)
+ Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\).
Chọn đáp án đúng
Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Qua M vẽ đường thẳng vuông góc với AB cắt AB tại H.
Chọn đáp án đúng
Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh là 10cm và 8cm.
Chọn câu trả lời đúng nhất
Tam giác ABC có chu vi bằng 18cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\). Chu vi tam giác A’B’C’ bằng:
Hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD theo tỉ số đồng dạng k. Biết rằng diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\), diện tích hình vuông ABCD là \(36c{m^2}.\) Khi đó, tỉ số đồng dạng k bằng:
Cho hình tròn H có diện tích bằng \(113,04c{m^2}\). Hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\). Khi đó, diện tích của hình tròn H’ bằng:
Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\). Biết rằng diện tích tam giác ABC bằng \(48c{m^2}.\) Diện tích tam giác AMN bằng:
Cho tam giác ABC. Trên cạnh BC lấy điểm K sao cho \(CK = \frac{2}{3}BC.\) Tìm trên AB điểm H sao cho cạnh HK là hình đồng dạng phối cảnh của cạnh AC (với tâm đồng dạng phối cảnh là điểm B)
: Cho hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 6cm,BC = 8cm,A'B' = 12cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ là:
Cho tam giác ABC có \(AB = 3cm,BC = 4cm,AC = 5cm.\) Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích tam giác A”B”C” bằng \(96c{m^2}\).
Chọn đáp án đúng
Cho hình chữ nhật ABCD có \(AB = \frac{3}{4}BC.\) Hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD theo tỉ số đồng dạng 2. Biết rằng \(A'C' = 10cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ bằng:
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3.\) Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:

Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3\) nên tam giác A’B’C’ và tam giác ABC là đồng dạng phối cảnh với tỉ số vị tự là 3.
Do đó tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là \(\frac{1}{3}\).
Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) với tâm phối cảnh là:
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Chọn đáp án đúng nhất
Đáp án : C
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
+ Hai hình H, H’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Do đó, cả A và B đều đúng
Cho hình chữ nhật ba hình chữ nhật ABCD, A’B’C’D’, A”B”C”D” sao cho:
+ Hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh
+ Hình A”B”C”D” bằng hình A’B’C’D’
Chọn đáp án đúng
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng
Vì hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh và hình A”B”C”D” bằng hình A’B’C’D’ nên
+ Hình A’B’C’D’ đồng dạng với hình ABCD
+ Hình A”B”C”D” đồng dạng với hình ABCD
Do đó, cả A, B đều đúng
Trong những cặp hình cho ở hình vẽ dưới đây, có mấy cặp hình là hình đồng dạng?

Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Các cặp hình đồng dạng là: Cặp hình 1 và cặp hình 2.
Vậy có 2 cặp hình đồng dạng.
Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA và OB.
Chọn đáp án đúng.
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.

Vì C là trung điểm của OA nên \(OC = \frac{1}{2}OA\)
Vì D là trung điểm của OB nên \(OD = \frac{1}{2}OB\)
Mà O là giao điểm của AC và BD nên cạnh CD là hình đồng dạng phối cảnh của cạnh AB với tỉ số đồng dạng \(k = \frac{1}{2}\), tâm phối cảnh là điểm O.
Do đó, cạnh CD là hình đồng dạng của cạnh AB với tỉ số \(k = \frac{1}{2}\)
Suy ra, cả A, B đều đúng.
Cho các hình vẽ sau:

Hình nào đồng dạng với hình a?
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì \(\frac{5}{5} \ne \frac{9}{{7,5}}\) nên hình a và hình b không phải là hai hình đồng dạng
Vì \(\frac{5}{{2,5}} = \frac{9}{{4,5}}\) nên hình a và hình c là hai hình đồng dạng với nhau
Vì \(\frac{{12}}{9} \ne \frac{4}{5}\) nên hình a và hình d không phải là hai hình đồng dạng
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng là: \(\frac{6}{3} = 2\)
Hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3.\) Nếu độ dài cạnh của hình vuông ABCD là 9cm thì độ dài cạnh của hình vuông A’B’C’D’ là:
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.
Vì hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3\) nên cạnh của hình vuông A’B’C’D’ gấp 3 lần cạnh của hình vuông ABCD. Do đó, cạnh của hình vuông A’B’C’D’ là: \(9.3 = 27\left( {cm} \right)\)
Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.

Cho các khẳng định sau:
+ Hình thang ABCD và EFGH bằng nhau
+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau
+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’
Có bao nhiêu khẳng định đúng?
Đáp án : D
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Hình thang ABCD và EFGH bằng nhau.
Vì các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD nên \(OA = 2OA',OB = 2OB',OC = 2OC',OD = 2OD'\).
Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’.
Do đó, hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau.
Vậy cả 3 khẳng định trên đều đúng
Cho tam giác ABC có AB = 4, BC = 7, CA = 6. Cho O, I là điểm phân biệt.
+ Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\)
+ Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\).
Chọn đáp án đúng
Đáp án : A
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh nên \(\frac{OA'}{OA}=\frac{OB'}{OB}=\frac{OC'}{OC}\) suy ra \( \Delta A'B'C'\backsim \Delta ABC\), do đó \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=3\)
suy ra \(A'B'=12;B'C'=21;C'A'=18\)
Vì tam giác A”B”C” là hình đồng dạng phối cảnh của tam giác ABC với I là tâm đồng dạng phối cảnh nên \(\frac{IA''}{IA}=\frac{IB''}{IB}=\frac{IC''}{IC}\) suy ra \( \Delta A''B''C''\backsim \Delta ABC\), do đó \(\frac{A''B''}{AB}=\frac{B''C''}{BC}=\frac{C''A''}{CA}=3\)
suy ra \(A''B''=12;B''C''=21;C''A''=18\)
Do đó, \(A'B'=A''B''=21,B'C'=B''C''=21,C'A'=C''A''=18\)
suy ra \(\frac{A''B''}{A'B'}=\frac{C''B''}{C'B'}=\frac{A''C''}{A'C'}=1\)
Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Qua M vẽ đường thẳng vuông góc với AB cắt AB tại H.
Chọn đáp án đúng
Đáp án : A
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H ’bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)

Ta có: \(HM \bot AB,AC \bot AB\) nên HM//AC
Tam giác ABC có: M là trung điểm của BC, HM//AC nên H là trung điểm của AB.
Do đó, \(\frac{{BH}}{{BA}} = \frac{1}{2}\)
Lại có: Mà là trung điểm của BC nên \(\frac{{BM}}{{BC}} = \frac{1}{2}\)
Suy ra: \(\frac{{BH}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{2}\)
Mà đường thẳng AH và MC cùng đi qua điểm B.
Do đó, HM là hình đồng dạng phối cảnh của cạnh AC, tâm B, tỉ số \(\frac{1}{2}\)
Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh là 10cm và 8cm.
Chọn câu trả lời đúng nhất
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H

Trên các đoạn thẳng EF, EG, EH, ta lần lượt lấy các điểm F”, G”, H” sao cho \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}.\) Theo định lý Thalès đảo ta có: F”G”//FG, G”H”//GH.
Mà \(\widehat{F''EH''}={{90}^{0}}\) nên tứ giác EF”G”H” là hình chữ nhật.
Mặt khác, ta có: \(\frac{EF''}{EF}=\frac{F''G''}{FG}=\frac{G''H''}{GH}=\frac{H''E}{HE}=\frac{4}{5}\) (hệ quả định lí Thalès)
Suy ra \(EF''=F''G''=G''H''=H''E=8cm\) .
Do đó, tứ giác EF”G”H” là hình vuông có độ dài cạnh bằng 8cm.
Suy ra, hai hình vuông EF”G”H” và E’F’G’H’ bằng nhau
Vì \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}\) nên hình vuông EF”G”H” đồng dạng phối cảnh với hình vuông EFGH hay hình vuông E’F’G’H’ đồng dạng phối cảnh với hình vuông EFGH.
Vậy hình vuông E’F’G’H’ đồng dạng với hình vuông EFGH.
Tam giác ABC có chu vi bằng 18cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\). Chu vi tam giác A’B’C’ bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Tam giác ABC có chu vi bằng 18cm nên \(AB + BC + CA = 18\)
Chu vi tam giác A’B’C’ là: \(P' = A'B' + A'C' + B'C'\)
Vì tam A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\) nên \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{3}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{{A'B' + A'C' + B'C'}}{{AB + AC + BC}} = \frac{{P'}}{{18}} = \frac{1}{3}\)
\( \Rightarrow P' = 18:3 = 6\left( {cm} \right)\)
Vậy chu vi tam giác A’B’C’ bằng 6cm
Hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD theo tỉ số đồng dạng k. Biết rằng diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\), diện tích hình vuông ABCD là \(36c{m^2}.\) Khi đó, tỉ số đồng dạng k bằng:
Đáp án : A
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H ’bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\) nên ta có: \(A'B{'^2} = 64 \Rightarrow A'B' = 8cm\)
Vì diện tích hình vuông ABCD là \(36c{m^2}\) nên ta có: \(A{B^2} = 36 \Rightarrow AB = 6cm\)
Vì hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD tỉ số đồng dạng k nên:
\(k = \frac{{A'B'}}{{AB}} = \frac{8}{6} = \frac{4}{3}\)
Vậy tỉ số đồng dạng là \(\frac{4}{3}\)
Cho hình tròn H có diện tích bằng \(113,04c{m^2}\). Hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\). Khi đó, diện tích của hình tròn H’ bằng:
Đáp án : C
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình tròn H có diện tích bằng \(113,04c{m^2}\) nên bán kính của hình tròn là: \({R^2} = \frac{{113,04}}{{3,14}} = 36 \Rightarrow R = 6cm\)
Vì hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\) nên bán kính hình tròn H’ là: \(R' = \frac{R}{2} = 3\left( {cm} \right)\)
Diện tích hình tròn H’ là: \({3^2}.3,14 = 28,26c{m^2}\)
Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\). Biết rằng diện tích tam giác ABC bằng \(48c{m^2}.\) Diện tích tam giác AMN bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)

Vì đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{4} \Rightarrow AB = 4AM,AC = 4AN\)
Diện tích tam giác AMN vuông tại A là: \({S_{AMN}} = \frac{1}{2}AM.AN\)
Vì tam giác ABC vuông tại A nên diện tích tam giác ABC là:
\(\frac{1}{2}AB.AC = 48 \Rightarrow \frac{1}{2}.4AM.4AN = 48 \Rightarrow \frac{1}{2}AM.AN = 3\left( {c{m^2}} \right)\)
Do đó, diện tích tam giác AMN bằng \(3c{m^2}\).
Cho tam giác ABC. Trên cạnh BC lấy điểm K sao cho \(CK = \frac{2}{3}BC.\) Tìm trên AB điểm H sao cho cạnh HK là hình đồng dạng phối cảnh của cạnh AC (với tâm đồng dạng phối cảnh là điểm B)
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)

Vì H thuộc AB và HK là hình đồng dạng phối cảnh của cạnh AC, với tâm đồng dạng phối cảnh là điểm B nên \(\frac{{HK}}{{AC}} = \frac{{BK}}{{BC}} = \frac{{BH}}{{BA}}\)
Mà \(CK = \frac{2}{3}BC \Rightarrow \frac{{BK}}{{BC}} = \frac{1}{3} \Rightarrow \frac{{BH}}{{BA}} = \frac{{KH}}{{AC}} = \frac{1}{3}\)
Do đó, điểm H cần tìm thuộc đoạn thẳng AB sao cho \(BH = \frac{1}{3}AB\).
: Cho hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 6cm,BC = 8cm,A'B' = 12cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ là:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k nên \(k = \frac{{A'B'}}{{AB}} = \frac{{12}}{6} = 2\)
Ta có: \(\frac{{B'C'}}{{BC}} = 2 \Rightarrow B'C' = 8.2 = 16\left( {cm} \right)\)
Diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 12.16 = 192\left( {c{m^2}} \right)\)
Cho tam giác ABC có \(AB = 3cm,BC = 4cm,AC = 5cm.\) Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích tam giác A”B”C” bằng \(96c{m^2}\).
Chọn đáp án đúng
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2 nên \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=2\)
\(\Rightarrow A'B'=6cm,B'C'=8cm,A'C'=10cm\)
Vì \(A'C{{'}^{2}}=A'B{{'}^{2}}+B'C{{'}^{2}}\left( {{10}^{2}}={{8}^{2}}+{{6}^{2}} \right)\) nên tam giác A’B’C’ vuông tại B’
Vì tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x nên \(\Delta A''B''C''\backsim \Delta A'B'C'\)
Do đó, \(\widehat{A''B''C''}=\widehat{A'B'C'}=90\) và \(\frac{A''B''}{A'B'}=\frac{A''C''}{A'C'}=\frac{B''C''}{B'C'}=x\Rightarrow A''B''=6x,A''C''=10x,B''C''=8x\)
Vì tam giác A”B”C” vuông tại B” nên diện tích tam giác A”B”C” là:
\({{S}_{A''B''C''}}=\frac{1}{2}B''A''.B''C''\Rightarrow \frac{1}{2}.6x.8x=96\Rightarrow {{x}^{2}}=4\Rightarrow x=2\) (do \(x>0\))
Cho hình chữ nhật ABCD có \(AB = \frac{3}{4}BC.\) Hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD theo tỉ số đồng dạng 2. Biết rằng \(A'C' = 10cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ bằng:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD có tỉ số đồng dạng 2 nên \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = 2\)
Mà \(AB = \frac{3}{4}BC \Rightarrow A'B' = \frac{3}{4}B'C'.\)
Vì A’B’C’D’ là hình chữ nhật nên \(\widehat {A'B'C'} = {90^0}\)
Do đó, tam giác A’B’C’ vuông tại B’. Áp dụng định lý Pytago vào tam giác A’B’C’ vuông tại B’ ta có: \(A'C{'^2} = A'B{'^2} + B'C{'^2}\) (1)
Thay \(A'B' = \frac{3}{4}B'C'\) vào (1) ta có:
\({\left( {\frac{3}{4}B'C'} \right)^2} + B'C{'^2} = {10^2}\)
\(\frac{{25}}{{16}}B'C{'^2} = 100\)
\(B'C{'^2} = 64\) nên \(B'C' = 8cm\)
Do đó, \(A'B' = 8.\frac{3}{4} = 6\left( {cm} \right)\)
Vậy diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 6.8 = 48\left( {c{m^2}} \right)\)
Bài 9: Hình đồng dạng trong chương trình Toán 8 Cánh diều tập trung vào việc giới thiệu khái niệm về hai hình đồng dạng, các trường hợp đồng dạng của tam giác và các tính chất liên quan. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học phức tạp hơn ở các lớp trên.
Hình đồng dạng có nhiều ứng dụng thực tế trong cuộc sống, chẳng hạn như:
Cho tam giác ABC và tam giác A'B'C' đồng dạng với nhau theo tỉ lệ k = 2. Biết AB = 5cm, BC = 7cm, CA = 9cm. Tính độ dài các cạnh của tam giác A'B'C'.
Giải:
Vì tam giác ABC đồng dạng với tam giác A'B'C' theo tỉ lệ k = 2, ta có:
Để nắm vững kiến thức và rèn luyện kỹ năng giải bài tập về hình đồng dạng, hãy truy cập giaitoan.edu.vn và tham gia các bài trắc nghiệm được thiết kế bởi đội ngũ giáo viên chuyên nghiệp. Các bài trắc nghiệm này không chỉ giúp bạn kiểm tra kiến thức mà còn cung cấp đáp án và lời giải chi tiết để bạn hiểu rõ hơn về các khái niệm và phương pháp giải.
Trắc nghiệm Bài 9: Hình đồng dạng Toán 8 Cánh diều là một công cụ hữu ích để giúp học sinh ôn tập và củng cố kiến thức. Hãy tận dụng tối đa các tài liệu và bài tập có sẵn tại giaitoan.edu.vn để đạt kết quả tốt nhất trong học tập.