Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 1 Toán 8 - Đề số 8, một công cụ hữu ích giúp các em học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 8, bao gồm các dạng bài tập thường gặp và có đáp án chi tiết đi kèm.
Với đề thi này, các em có thể tự tin làm bài và kiểm tra kiến thức đã học, đồng thời phát hiện những lỗ hổng để khắc phục kịp thời.
Trong các biểu thức đại số sau, biểu thức nào không phải đơn thức?
\(2\).
\({x^3}{y^2}\).
\(5x + 9\).
\(x\).
Tìm hệ số trong đơn thức \(\frac{1}{3}a{b^2}xy\) với a, b là hằng số
\(\frac{1}{3}\).
\(\frac{1}{3}{a^2}b\).
\(\frac{1}{3}a{b^2}\).
\(xy\).
Tất cả các hạng tử của đa thức \(B = 3{x^2} - 2x + 1\) là
\(3{x^2}\); \( - 2x\) và 1.
\(3{x^2}\) và \( - 2x\).
\(3\); \( - 2\) và 1.
\( - 2x\) và 1.
Trong các đơn thức sau, đơn thức nào đồng dạng với đơn thức \( - 3{x^2}yz\)?
\( - 3xyz\).
\(\frac{2}{3}{x^2}yz\).
\(\frac{3}{2}z{x^2}\).
\(4{x^2}y\).
Bậc của đa thức \({x^2}{y^2}\; + {\rm{ }}x{y^5}\; - {\rm{ }}{x^2}{y^4}\) là
7.
6.
5.
4.
Điền vào chỗ trống sau: \({\left( {x + 2} \right)^2} = {x^2} + ... + 4\)
\(2x\).
\(4x\).
\(2\).
\(4\).
Biểu thức \({x^3} + 64\) được viết dưới dạng tích là
\(\left( {x - 4} \right)\left( {{x^2} + 4x + 16} \right)\).
\(\left( {x - 4} \right)\left( {{x^2} + 4x - 16} \right)\)
\(\left( {x + 4} \right)\left( {{x^2} + 4x + 16} \right)\).
\(\left( {x + 4} \right)\left( {{x^2} - 4x + 16} \right)\).
Kết quả của phép tính \(\left( {x - 3y} \right)\left( {x + 3y} \right)\) là
\({x^2} - 9{y^2}\).
\({x^2} - 6xy + 9{y^2}\).
\({x^2} + 6xy + 9{y^2}\).
\({x^2} - 9xy + 9{y^2}\).
Với điều kiện của \(x\) thì phân thức \(\frac{{x - 3}}{{6x + 24}}\) xác định?
\(x \ne 2\).
\(x \ne 3\).
\(x \ne - 4\).
\(x \ne 4\).
Kết quả của phép tính \(\frac{{2x + 1}}{{x - 3}} + \frac{5}{{3 - x}}\) là:
\(\frac{{2x + 4}}{{x - 3}}\).
\(\frac{{2x - 4}}{{x - 3}}\).
\(\frac{{2x + 4}}{{{{\left( {x - 3} \right)}^2}}}\).
\(\frac{{2x + 6}}{{x - 3}}\).
Hình chóp tam giác đều có mặt bên là hình gì?
Tam giác cân.
Tam giác vuông.
Tam giác vuông cân.
Tam giác đều.
Một chậu cây cảnh mini có hình dạng là hình chóp tứ giác đều có cạnh đáy bằng \(24{\rm{ }}cm\), chiều cao bằng \(35{\rm{ }}cm\). Thể tích của hình chóp bằng

\(20\,160\,c{m^3}\).
\(840\,c{m^3}\).
\(3\,360\,c{m^3}\).
\(6\,720\,c{m^3}\).
Thực hiện phép tính:
a) \({\left( {2x + 3} \right)^2}\);
b) \((15{x^4}{y^5} - 30{x^3}{y^4} + 5{x^5}{y^4}):(5{x^3}{y^3})\);
c) \(\left( {x + 3} \right)\left( {{x^2} + 3x - 5} \right)\).
Phân tích đa thức thành nhân tử:
a) \(4{x^2} - 25\);
b) \(x(x - 7) - 3x + 21\).
Cho biểu thức \(A = \frac{{5x - 2}}{{{x^2} - 4}} - \frac{3}{{x + 2}} + \frac{x}{{x - 2}}\).
a) Tìm điều kiện xác định của biểu thức \(A.\)
b) Rút gọn biểu thức \(A.\)
c) Tính giá trị của biểu thức \(A\) với \(x\) thỏa mãn \(\left| {x + 3} \right| = 5.\)
1. Chiếc hộp (Hình a) được vẽ lại như Hình b có dạng hình chóp tam giác đều S.MNP.
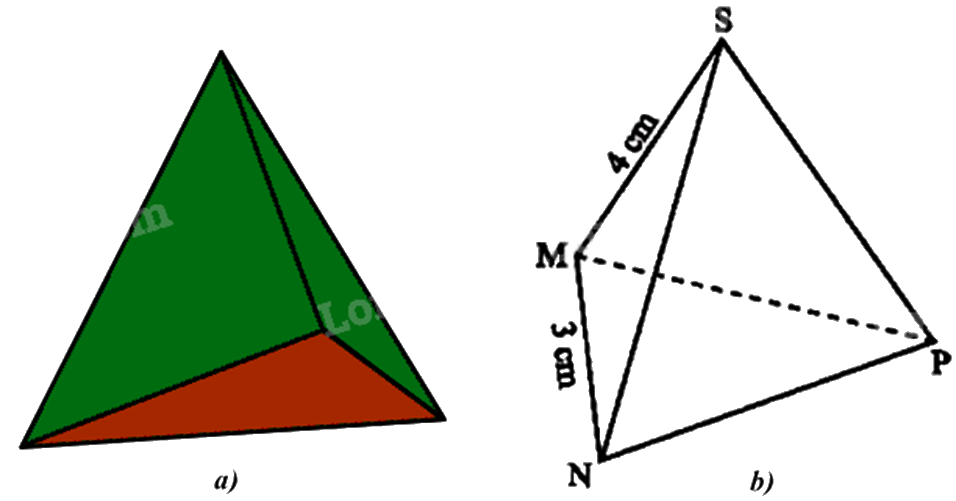
a) Hãy cho biết mặt đáy, mặt bên, cạnh bên của chiếc hộp đó.
b) Cho biết SM = 4cm, MN = 3 cm. Tìm độ dài các cạnh còn lại của chiếc hộp.
2. Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.

a) Cạnh bên của hình chóp là bao nhiêu?
b) Tính thể tích hình chóp.
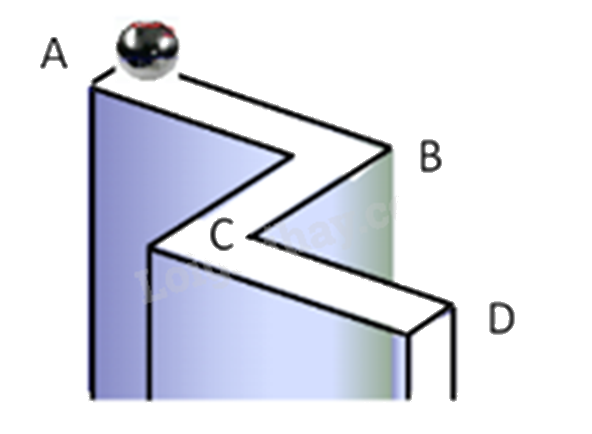
Một viên bi lăn theo đoạn đường từ A đến D như hình vẽ \((AB \bot BC,BC \bot CD)\). Hãy tính khoảng cách AD. Biết rằng AB = 10m, BC = 12m, CD = 6m.
Trong các biểu thức đại số sau, biểu thức nào không phải đơn thức?
\(2\).
\({x^3}{y^2}\).
\(5x + 9\).
\(x\).
Đáp án : C
Dựa vào khái niệm đơn thức: Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.
Biểu thức \(5x + 9\) không phải là đơn thức.
Đáp án C.
Tìm hệ số trong đơn thức \(\frac{1}{3}a{b^2}xy\) với a, b là hằng số
\(\frac{1}{3}\).
\(\frac{1}{3}{a^2}b\).
\(\frac{1}{3}a{b^2}\).
\(xy\).
Đáp án : C
Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.
Vì a, b là hằng số nên hệ số trong đơn thức là \(\frac{1}{3}a{b^2}\).
Đáp án C.
Tất cả các hạng tử của đa thức \(B = 3{x^2} - 2x + 1\) là
\(3{x^2}\); \( - 2x\) và 1.
\(3{x^2}\) và \( - 2x\).
\(3\); \( - 2\) và 1.
\( - 2x\) và 1.
Đáp án : A
Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Các hạng tử của đa thức là: \(3{x^2}\); \( - 2x\) và 1.
Đáp án A.
Trong các đơn thức sau, đơn thức nào đồng dạng với đơn thức \( - 3{x^2}yz\)?
\( - 3xyz\).
\(\frac{2}{3}{x^2}yz\).
\(\frac{3}{2}z{x^2}\).
\(4{x^2}y\).
Đáp án : B
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Đơn thức \(\frac{2}{3}{x^2}yz\) có cùng phần biến \({x^2}yz\) với đơn thức \( - 3{x^2}yz\) nên là hai đơn thức đồng dạng.
Đáp án B.
Bậc của đa thức \({x^2}{y^2}\; + {\rm{ }}x{y^5}\; - {\rm{ }}{x^2}{y^4}\) là
7.
6.
5.
4.
Đáp án : B
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức.
Đa thức \({x^2}{y^2}\; + {\rm{ }}x{y^5}\; - {\rm{ }}{x^2}{y^4}\) gồm 3 đơn thức \({x^2}{y^2};{\rm{ }}x{y^5};\; - {\rm{ }}{x^2}{y^4}\) với bậc lần lượt là \(4;6;6\).
Do đó bậc của đa thức \({x^2}{y^2}\; + {\rm{ }}x{y^5}\; - {\rm{ }}{x^2}{y^4}\) là 6.
Đáp án B.
Điền vào chỗ trống sau: \({\left( {x + 2} \right)^2} = {x^2} + ... + 4\)
\(2x\).
\(4x\).
\(2\).
\(4\).
Đáp án : B
Dựa vào hằng đẳng thức bình phương của một tổng.
Ta có: \({\left( {x + 2} \right)^2} = {x^2} + 4x + 4\).
Chỗ trống cần điền là \(4x\).
Đáp án B.
Biểu thức \({x^3} + 64\) được viết dưới dạng tích là
\(\left( {x - 4} \right)\left( {{x^2} + 4x + 16} \right)\).
\(\left( {x - 4} \right)\left( {{x^2} + 4x - 16} \right)\)
\(\left( {x + 4} \right)\left( {{x^2} + 4x + 16} \right)\).
\(\left( {x + 4} \right)\left( {{x^2} - 4x + 16} \right)\).
Đáp án : D
Dựa vào hằng đẳng thức tổng hai lập phương.
Ta có:
\({x^3} + 64 = {x^3} + {4^3} = \left( {x + 4} \right)\left( {{x^2} - 4x + 16} \right)\).
Đáp án D.
Kết quả của phép tính \(\left( {x - 3y} \right)\left( {x + 3y} \right)\) là
\({x^2} - 9{y^2}\).
\({x^2} - 6xy + 9{y^2}\).
\({x^2} + 6xy + 9{y^2}\).
\({x^2} - 9xy + 9{y^2}\).
Đáp án : A
Dựa vào hằng đẳng thức hiệu hai bình phương.
Ta có:
\(\left( {x - 3y} \right)\left( {x + 3y} \right) = {x^2} - {\left( {3y} \right)^2} = {x^2} - 9{y^2}\).
Đáp án A.
Với điều kiện của \(x\) thì phân thức \(\frac{{x - 3}}{{6x + 24}}\) xác định?
\(x \ne 2\).
\(x \ne 3\).
\(x \ne - 4\).
\(x \ne 4\).
Đáp án : C
Điều kiện của biến để giá trị tương ứng của mẫu thức khác 0 được gọi điều kiện để giá trị của phân thức được xác định.
Phân thức \(\frac{{x - 3}}{{6x + 24}}\) xác định khi và chỉ khi \(6x + 24 \ne 0\) tức là \(x \ne - 4\).
Đáp án C.
Kết quả của phép tính \(\frac{{2x + 1}}{{x - 3}} + \frac{5}{{3 - x}}\) là:
\(\frac{{2x + 4}}{{x - 3}}\).
\(\frac{{2x - 4}}{{x - 3}}\).
\(\frac{{2x + 4}}{{{{\left( {x - 3} \right)}^2}}}\).
\(\frac{{2x + 6}}{{x - 3}}\).
Đáp án : B
Đưa hai phân thức về cùng mẫu để thực hiện phép cộng.
Ta có:
\(\frac{{2x + 1}}{{x - 3}} + \frac{5}{{3 - x}} = \frac{{2x + 1}}{{x - 3}} - \frac{5}{{x - 3}} = \frac{{2x + 1 - 5}}{{x - 3}} = \frac{{2x - 4}}{{x - 3}}\).
Đáp án B.
Hình chóp tam giác đều có mặt bên là hình gì?
Tam giác cân.
Tam giác vuông.
Tam giác vuông cân.
Tam giác đều.
Đáp án : A
Dựa vào đặc điểm của hình chóp tam giác đều.
Hình chóp tam giác đều có mặt bên là tam giác cân.
Đáp án A.
Một chậu cây cảnh mini có hình dạng là hình chóp tứ giác đều có cạnh đáy bằng \(24{\rm{ }}cm\), chiều cao bằng \(35{\rm{ }}cm\). Thể tích của hình chóp bằng

\(20\,160\,c{m^3}\).
\(840\,c{m^3}\).
\(3\,360\,c{m^3}\).
\(6\,720\,c{m^3}\).
Đáp án : D
Sử dụng công thức tính thể tích hình chóp: \(V = S.h\) (S là diện tích đáy, h là chiều cao)
Thể tích của hình chóp là:
\(V = \frac{1}{3}{.24^2}.35 = 6\,720\,\left( {c{m^3}} \right)\).
Đáp án D.
Thực hiện phép tính:
a) \({\left( {2x + 3} \right)^2}\);
b) \((15{x^4}{y^5} - 30{x^3}{y^4} + 5{x^5}{y^4}):(5{x^3}{y^3})\);
c) \(\left( {x + 3} \right)\left( {{x^2} + 3x - 5} \right)\).
a) Sử dụng hằng đẳng thức bình phương của một tổng.
b) Sử dụng quy tắc chia đa thức cho đơn thức.
c) Sử dụng quy tắc nhân đa thức với đa thức.
a) \({\left( {2x + 3} \right)^2}\)
\( = {\left( {2x} \right)^2} + 2.2x.3 + {3^2}\)
\( = 4{x^2} + 12x + 9\)
b) \((15{x^4}{y^5} - 30{x^3}{y^4} + 5{x^5}{y^4}):(5{x^3}{y^3})\)
\( = 15{x^4}{y^5}:5{x^3}{y^3} - 30{x^3}{y^4}:5{x^3}{y^3} + 5{x^5}{y^4}:5{x^3}{y^3}\)
\( = 3x{y^2} - 6y + {x^2}y\)
c) \(\left( {x + 3} \right)\left( {{x^2} + 3x - 5} \right)\)
\( = {x^3} + 3{x^2} - 5x + 3{x^2} + 9x - 15\)
\( = {x^3} + 6{x^2} + 4x - 15\)
Phân tích đa thức thành nhân tử:
a) \(4{x^2} - 25\);
b) \(x(x - 7) - 3x + 21\).
Sử dụng các phương pháp phân tích đa thức thành nhân tử phù hợp.
a) \(4{x^2} - 25\)
\(\begin{array}{l} = {\left( {2x} \right)^2} - {5^2}\\ = \left( {2x - 5} \right)\left( {2x + 5} \right)\end{array}\)
b) \(x(x - 7) - 3x + 21\)
\(\begin{array}{l} = x(x - 7) - 3\left( {x - 7} \right)\\ = \left( {x - 7} \right)\left( {x - 3} \right)\end{array}\)
Cho biểu thức \(A = \frac{{5x - 2}}{{{x^2} - 4}} - \frac{3}{{x + 2}} + \frac{x}{{x - 2}}\).
a) Tìm điều kiện xác định của biểu thức \(A.\)
b) Rút gọn biểu thức \(A.\)
c) Tính giá trị của biểu thức \(A\) với \(x\) thỏa mãn \(\left| {x + 3} \right| = 5.\)
a) Điều kiện của biến để giá trị tương ứng của mẫu thức khác 0 được gọi điều kiện để giá trị của phân thức được xác định.
b) Thực hiện phép tính cộng, trừ với phân thức đại số để rút gọn.
c) Tìm giá trị của \(x\) thỏa mãn \(\left| {x + 3} \right| = 5.\)
Kiểm tra điều kiện của \(x\).
Với giá trị \(x\) thỏa mãn, thay vào A để tính giá trị.
a) Điều kiện xác định của biểu thức \(A\) là:
\({x^2} - 4 \ne 0\), \(x + 2 \ne 0\) và \(x - 2 \ne 0\). Tức là \(x \ne \pm 2.\)
b) Với \(x \ne \pm 2,\) ta có:
\(A = \frac{{5x - 2}}{{{x^2} - 4}} - \frac{3}{{x + 2}} + \frac{x}{{x - 2}}\)
\( = \frac{{5x - 2 - 3\left( {x - 2} \right) + x\left( {x + 2} \right)}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}\)
\( = \frac{{5x - 2 - 3x + 6 + {x^2} + 2x}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}\)
\( = \frac{{{x^2} + 4x + 4}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}\)
\( = \frac{{{{\left( {x + 2} \right)}^2}}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} = \frac{{x + 2}}{{x - 2}}\).
c) Ta có: \(\left| {x + 3} \right| = 5\)
\(x + 3 = 5\) hoặc \(x + 3 = - 5\)
\(x = 2\) (không thỏa mãn) hoặc \(x = - 8\) (thỏa mãn)
Thay \(x = - 8\) vào biểu thức \(A = \frac{{x + 2}}{{x - 2}}\) ta được:
\(A = \frac{{ - 8 + 2}}{{ - 8 - 2}} = \frac{{ - 6}}{{ - 10}} = \frac{3}{5}.\)
1. Chiếc hộp (Hình a) được vẽ lại như Hình b có dạng hình chóp tam giác đều S.MNP.
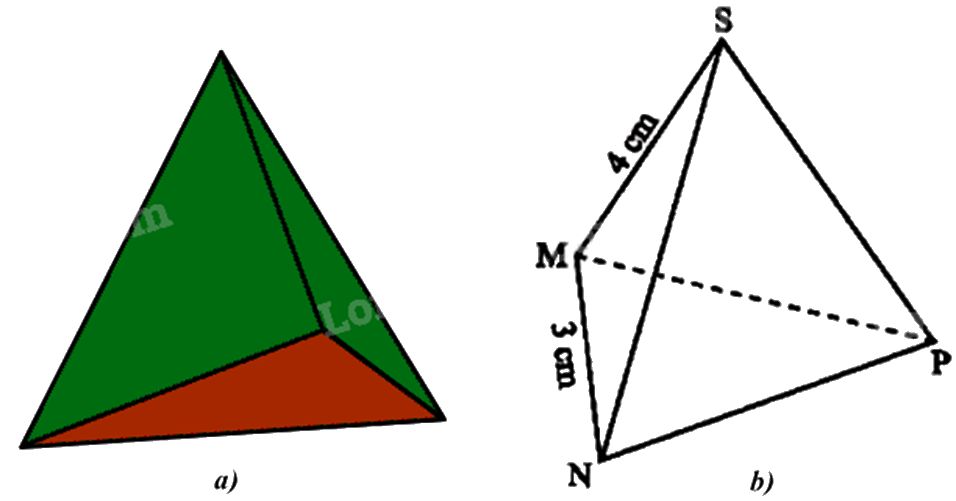
a) Hãy cho biết mặt đáy, mặt bên, cạnh bên của chiếc hộp đó.
b) Cho biết SM = 4cm, MN = 3 cm. Tìm độ dài các cạnh còn lại của chiếc hộp.
2. Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.

a) Cạnh bên của hình chóp là bao nhiêu?
b) Tính thể tích hình chóp.
1. Dựa vào đặc điểm của hình chóp tam giác đều để xác định.
2. a) Sử dụng định lí Pythagore vào tam giác vuông để tính cạnh bên của hình chóp.
b) Sử dụng công thức tính thể tích hình chóp tứ giác đều: \(V = S.h\) (S là diện tích đáy, h là chiều cao).
1.
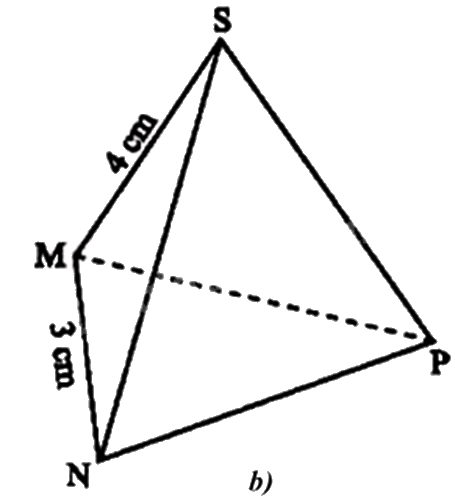
a) Mặt đáy là: (MNP).
Các mặt bên là: (SMN), (SNP), (SMP).
Các cạnh bên là: SM, SN, SP.
b) Độ dài các cạnh còn lại của chiếc hộp là:
SN = SP = SM = 4cm;
NP = MP = MN = 3cm.
2.
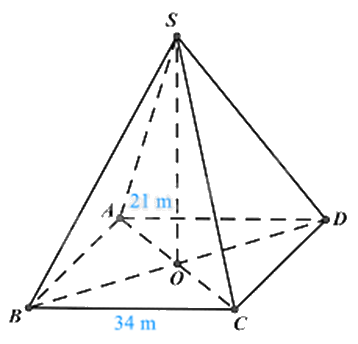
Giả sử kim tự tháp Lu-vrơ (Louvre)là hình chóp tứ giác đều S.ABCD.
Hình chóp tứ giác đều S.ABCD có ABCD là hình vuông nên AC = BD nên AO = OB.
Áp dụng định lí Pythagore vào tam giác vuông AOB, ta có:
\(\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\2A{O^2} = {34^2}\\A{O^2} = {34^2}:2 = 1156:2 = 578\end{array}\)
Vì S.ABCD là hình chóp tứ giác đều nên \(SO \bot AO\), suy ra \(\Delta SAO\) vuông tại O.
Áp dụng định lí Pythagore vào tam giác vuông SAO, ta có:
\(S{A^2} = S{O^2} + A{O^2} = {21^2} + 578 = 1019\).
Suy ra \(SA = \sqrt {1019} \approx 31,9\left( m \right)\).
b) Thể tích kim tự tháp là:
\(V = \frac{1}{3}{.34^2}.21 = 8092\left( {{m^3}} \right)\).
Một viên bi lăn theo đoạn đường từ A đến D như hình vẽ \((AB \bot BC,BC \bot CD)\). Hãy tính khoảng cách AD. Biết rằng AB = 10m, BC = 12m, CD = 6m.
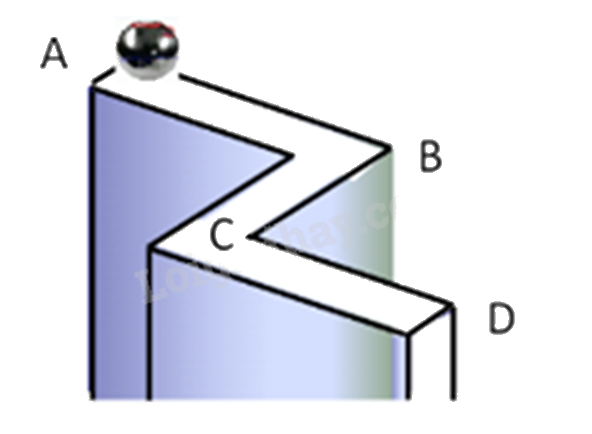
Từ D vẽ \(Dx \bot CD\) cắt AB tại E.
Chứng minh BCDE là hình chữ nhật, sử dụng tính chất của hình chữ nhật để tính BE, suy ra độ dài AE.
Dựa vào định lí Pythagore để tính cạnh AD.
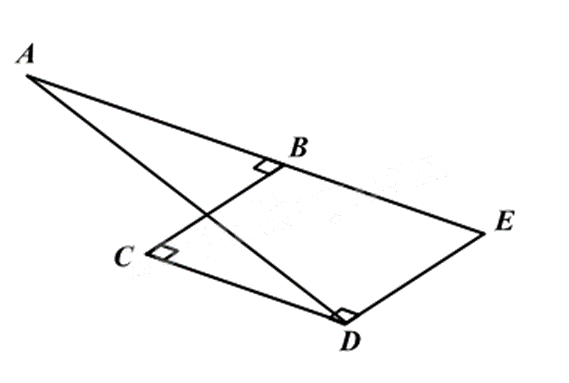
Từ D vẽ \(Dx \bot CD\) cắt AB tại E.
Mà \(BC \bot CD\) nên \(DE//BC\).
Vì \(AB \bot BC,BC \bot CD\) nên \(AB//CD\).
Xét tứ giác BCDE có \(\widehat B = \widehat C = \widehat D = 90^\circ \) nên BCDE là hình chữ nhật.
Suy ra \(DE = BC = 12m\); \(BE = CD = 6m\); \(\widehat E = 90^\circ \).
Dẫn đến \(AE = AB + BE = 10 + 6 = 16\left( m \right)\)
Áp dụng định lí Pythagore vào tam giác ADE vuông tại E, ta có:
\(AD = \sqrt {A{E^2} + D{E^2}} = \sqrt {{{16}^2} + {{12}^2}} = 20\left( m \right)\)
Vậy khoảng cách AD là 20m.
Kỳ thi giữa học kỳ 1 Toán 8 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh trong giai đoạn đầu năm học. Đề thi giữa kì 1 Toán 8 - Đề số 8 được thiết kế để kiểm tra kiến thức và kỹ năng giải toán của học sinh, bao gồm các chủ đề chính như:
Đề thi thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về đề thi và cách giải các bài toán, giaitoan.edu.vn cung cấp đáp án chi tiết và lời giải đầy đủ cho từng câu hỏi. Dưới đây là một số ví dụ về cách giải các bài toán thường gặp trong đề thi:
Lời giải:
Lời giải:
Diện tích hình chữ nhật = chiều dài x chiều rộng = 8cm x 5cm = 40cm2
Để đạt kết quả tốt trong môn Toán 8, học sinh cần:
Việc luyện tập đề thi giữa kì 1 Toán 8 - Đề số 8 không chỉ giúp học sinh làm quen với cấu trúc đề thi mà còn giúp các em:
Giaitoan.edu.vn cam kết cung cấp cho học sinh những tài liệu học tập chất lượng, đáp ứng nhu cầu học tập và ôn luyện của các em. Chúng tôi hy vọng rằng Đề thi giữa kì 1 Toán 8 - Đề số 8 sẽ là một công cụ hữu ích giúp các em đạt kết quả tốt nhất trong kỳ thi sắp tới.
| Chủ đề | Mức độ quan trọng |
|---|---|
| Đại số | Cao |
| Hình học | Cao |
| Bài tập thực tế | Trung bình |
| Lưu ý: Mức độ quan trọng có thể thay đổi tùy theo từng trường và từng đề thi. | |