Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 8 - Đề số 2 chương trình Chân trời sáng tạo. Đề thi này được biên soạn bám sát chương trình học, giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, giúp học sinh đánh giá được kiến thức đã học và chuẩn bị tốt nhất cho kỳ thi sắp tới.
Cho hàm số \(y = f(x) = {x^2}.\) Tính \(f\left( { - 5} \right) + f\left( 5 \right)\) .
Thanh long là một loại cây chịu hạn , không kén đất, rất thích hợp với điều kiện khí hậu và thổ nhưỡng của tỉnh Bình Thuận. Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng. Công thức biểu thị số tiền y(đồng) mà người mua phải trả khi mua x(kg) thanh long ruột đỏ loại I là :
Màn hình ra đa của một đài gợi lên hình ảnh một mặt phẳng tọa độ. Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ mấy trong mặt phẳng tọa độ Oxy ?
Trong mặt phẳng tọa độ Oxy như hình vẽ. Câu trả lời nào sau đây không đúng ?
D(-3;1).
Hàm số nào sau đây là hàm số bậc nhất?
Hệ số góc của hàm số \(y = - x - 3\) là:
Viết tỉ số cặp đoạn thằng có độ dài như sau: AB = 4dm; CD = 20dm.
Tìm giá trị của x trong hình vẽ?
Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.
Cho hình vẽ sau. Biết MN // BC, AM = 2cm, BM = 3cm, AN = 3cm. Độ dài đoạn thẳng NC bằng:
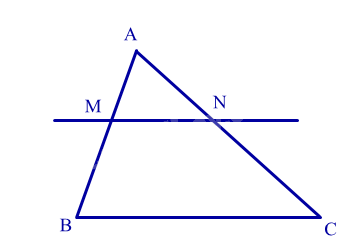
Cho tam giác ABC có P, Q lần lượt là trung điểm của AB và AC. Biết BC = 10cm. Ta có:
Cho \(\Delta ABC\), AD là tia phân giác trong của góc A. Hãy chọn câu đúng.
Cho hàm số \(y = - 2x + 1\) (1).
a) Chứng minh các điểm \(A\left( {0;1} \right)\) và \(B\left( {\frac{3}{2}; - 2} \right)\) thuộc đồ thị của hàm số (1) trong mặt phẳng tọa độ Oxy.
b) Biểu diễn A và B trong mặt phẳng tọa độ Oxy.
c) Tìm tọa độ điểm C nằm trên trục hoành và thuộc đồ thị của hàm số (1) trong mặt phẳng tọa độ Oxy.
Học sinh khối 8 ở một trường góp tiền để làm một album ca nhạc Tết Nguyên Đán 2024. Một phòng thu âm cho biết giá sản xuất đĩa gốc là 10 triệu đồng và mỗi đĩa in sao là 60 000 đồng.
a) Gọi x là số đĩa cần in sao và y là số tiền học sinh khối 8 phải trả (bao gồm tiền đĩa in sao và một đĩa gốc). Hãy biểu diễn y theo x. Hỏi y có phải là hàm số bậc nhất không? Vì sao?
b) Các bạn khối 8 cần góp bao nhiêu tiền để in được 150 đĩa sao và một đĩa gốc?
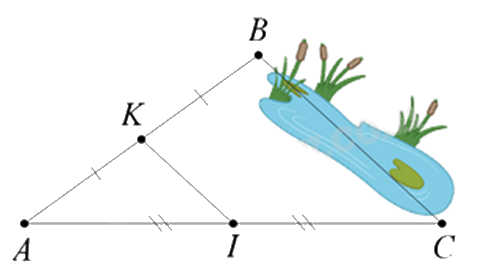
Giữa hai điểm \(B\) và \(C\) bị ngăn cách bởi hồ nước (như hình dưới). Hãy xác định độ dài \(BC\) mà không cần phải bơi qua hồ. Biết rằng đoạn thẳng \(KI\) dài \(30m\) và \(K\) là trung điểm của \(AB\), \(I\) là trung điểm của \(AC\).
Cho tam giác ABC vuông tại A. Gọi O là trung điểm của AC. Trên tia BO lấy điểm D sao cho O là trung điểm của BD.
a) Chứng minh tứ giác ABCD là hình bình hành.
b) Trên tia BA lấy điểm E sao cho A là trung điểm của BE. Chứng minh rằng AC = ED.
c) Qua O kẻ OM, ON lần lượt là phân giác của các góc BOA và BOC (\(M \in AB,N \in BC\)).
Chứng minh rằng MN // AC và BO đi qua trung điểm của MN.
Cho đường thẳng d: y = mx + m – 1. Tìm m để d cắt Ox tại A và cắt Oy tại B sao cho tam giác AOB vuông cân.
Cho hàm số \(y = f(x) = {x^2}.\) Tính \(f\left( { - 5} \right) + f\left( 5 \right)\) .
Đáp án : C
Thay x = -5; x = 5 vào hàm số.
Tính \(f\left( { - 5} \right) + f\left( 5 \right)\).
Ta có:
\(\begin{array}{l}f\left( { - 5} \right) = {\left( { - 5} \right)^2} = 25\\f\left( 5 \right) = {5^2} = 25\\ \Rightarrow f\left( { - 5} \right) + f\left( 5 \right) = 25 + 25 = 50\end{array}\)
Thanh long là một loại cây chịu hạn , không kén đất, rất thích hợp với điều kiện khí hậu và thổ nhưỡng của tỉnh Bình Thuận. Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng. Công thức biểu thị số tiền y(đồng) mà người mua phải trả khi mua x(kg) thanh long ruột đỏ loại I là :
Đáp án : C
Biểu thị y theo x.
Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng nên giá bán x (kg) thanh long là: 32 000.x (đồng).
Vậy ta có công thức biểu thị là y = 32 000x.
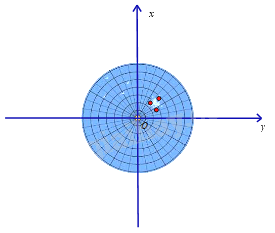
Màn hình ra đa của một đài gợi lên hình ảnh một mặt phẳng tọa độ. Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ mấy trong mặt phẳng tọa độ Oxy ?
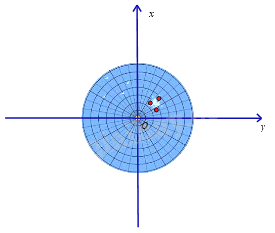
Đáp án : A
Dựa vào kiến thức về các góc phần tư.
Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ I.
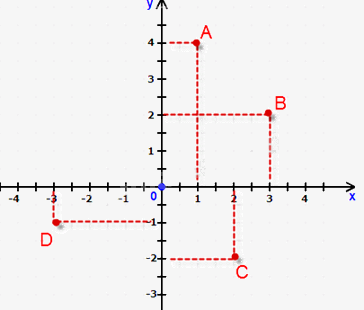
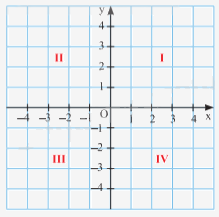
Trong mặt phẳng tọa độ Oxy như hình vẽ. Câu trả lời nào sau đây không đúng ?
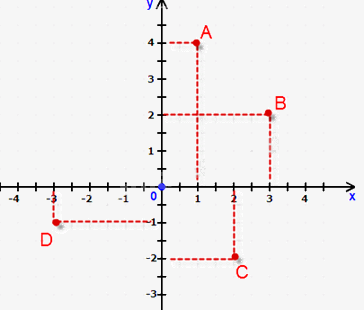
D(-3;1).
Đáp án : D
Quan sát hình vẽ để xác định tọa độ các điểm.
Hình chiếu của điểm A trên trục hoành là 1, trên trục tung là 4 nên tọa độ điểm A là A(1; 4). => A đúng.
Hình chiếu của điểm B trên trục hoành là 3, trên trục tung là 2 nên tọa độ điểm B là B(3; 2). => B đúng.
Hình chiếu của điểm C trên trục hoành là 2, trên trục tung là -2 nên tọa độ điểm C là C(2;-2). => C đúng.
Hình chiếu của điểm D trên trục hoành là -3, trên trục tung là -1 nên tọa độ điểm D là C(-3;-1). => D sai.
Hàm số nào sau đây là hàm số bậc nhất?
Đáp án : A
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\).
Hàm số \(y = 2x - 1\) là hàm số bậc nhất vì có dạng \(y = ax + b\) và hệ số \(a = 2 \ne 0\).
Hàm số \(y = - {x^2} + 3\) không là hàm số bậc nhất vì có \({x^2}\).
Hàm số \(y = \frac{1}{x}\) không là hàm số bậc nhất vì có x nằm ở mẫu.
Hàm số \(y = 2024\) không là hàm số bậc nhất vì hệ số \(a = 0\).
Hệ số góc của hàm số \(y = - x - 3\) là:
Đáp án : B
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\) với a là hệ số góc.
Hệ số góc của hàm số \(y = - x - 3\) làa = -1.
Viết tỉ số cặp đoạn thằng có độ dài như sau: AB = 4dm; CD = 20dm.
Đáp án : B
Sử dụng kiến thức về tỉ số của hai đoạn thẳng.
Ta có: \(\frac{{AB}}{{CD}} = \frac{4}{{20}} = \frac{1}{5}\).
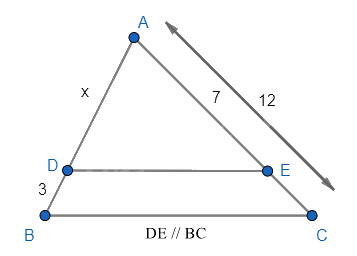
Tìm giá trị của x trong hình vẽ?
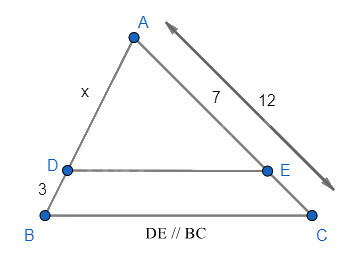
Đáp án : A
Áp dụng định lí Thalès để tính x.
Vì DE // BC nên \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} \Leftrightarrow \frac{x}{{x + 3}} = \frac{7}{{12}}\)
\(\begin{array}{l} \Leftrightarrow 12x = 7\left( {x + 3} \right) \Leftrightarrow 12x = 7x + 21\\ \Leftrightarrow 12x - 7x = 21 \Leftrightarrow 5x = 21 \Leftrightarrow x = \frac{{21}}{5}\end{array}\)
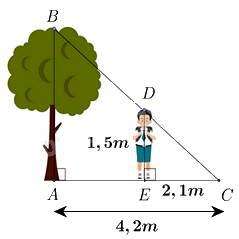
Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.
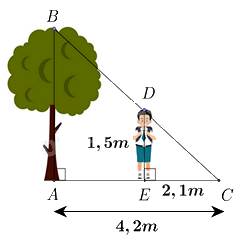
Đáp án : A
Dựa vào hệ quả của định lí Thales trong tam giác.
Vì cái cây và người đều vuông góc với mặt đất nên AB // DE.
Áp dụng hệ quả của định lí Thales vào tam giác ABC có DE // AB, ta có:
\(\frac{{CE}}{{AC}} = \frac{{DE}}{{AB}}\)
\(\frac{{2,1}}{{4,2}} = \frac{{1,5}}{{AB}} \Rightarrow AB = 1,5:\frac{{2,1}}{{4,2}} = 3\left( m \right)\)
Cho hình vẽ sau. Biết MN // BC, AM = 2cm, BM = 3cm, AN = 3cm. Độ dài đoạn thẳng NC bằng:
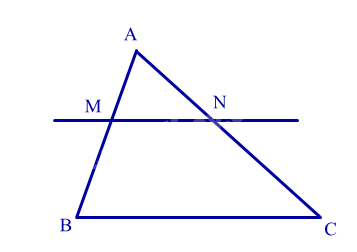
Đáp án : B
Dựa vào định lí Thales trong tam giác.
Áp dụng định lí Thales vào tam giác ABC có MN // BC, ta có:
\(\begin{array}{l}\frac{{AM}}{{BM}} = \frac{{AN}}{{NC}}\\\frac{2}{3} = \frac{3}{{NC}} \Rightarrow NC = 3:\frac{2}{3} = 4,5\left( {cm} \right)\end{array}\)
Cho tam giác ABC có P, Q lần lượt là trung điểm của AB và AC. Biết BC = 10cm. Ta có:
Đáp án : B
Dựa vào tính chất của đường trung bình.
Xét tam giác ABC có P, Q lần lượt là trung điểm của AB và AC nên PQ là đường trung bình của tam giác ABC \( \Rightarrow PQ = \frac{1}{2}BC = \frac{1}{2}.10 = 5\left( {cm} \right)\).
Cho \(\Delta ABC\), AD là tia phân giác trong của góc A. Hãy chọn câu đúng.
Đáp án : B
Sử dụng tính chất của đường phân giác trong tam giác.
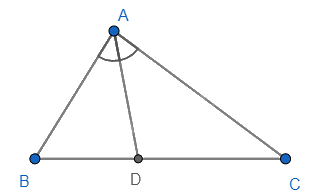
Theo tính chất của đường phân giác trong tam giác, ta có: \(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\) nên B đúng.
Cho hàm số \(y = - 2x + 1\) (1).
a) Chứng minh các điểm \(A\left( {0;1} \right)\) và \(B\left( {\frac{3}{2}; - 2} \right)\) thuộc đồ thị của hàm số (1) trong mặt phẳng tọa độ Oxy.
b) Biểu diễn A và B trong mặt phẳng tọa độ Oxy.
c) Tìm tọa độ điểm C nằm trên trục hoành và thuộc đồ thị của hàm số (1) trong mặt phẳng tọa độ Oxy.
a) Thay tọa độ của A, B vào hàm số để chứng minh.
b) Dựa vào các bước xác định một điểm với tọa độ cho trước trên mặt phẳng.
c) Điểm nằm trên trục hoành có tung độ bằng 0. Thay y = 0 vào để tìm hoành độ của C.
a) Ta có: \( - 2.0 + 1 = 1 \Rightarrow A\left( {0;1} \right)\) thuộc đồ thị của hàm số (1) (đpcm)
\( - 2.\frac{3}{2} + 1 = - 3 + 1 = - 2 \Rightarrow B\left( {\frac{3}{2}; - 2} \right)\) thuộc đồ thị của hàm số (1) (đpcm).
b) Biểu diễn A trong mặt phẳng tọa độ Oxy:
- Điểm A có hoành độ bằng 0 nên nằm trên trục tung.
- Trên trục tung lấy điểm 1 ta được điểm \(A\left( {0;1} \right)\).
Biểu diễn B trong mặt phẳng tọa độ Oxy.
- Trên trục hoành lấy điểm \(\frac{3}{2}\), vẽ đường thẳng vuông góc với trục hoành tại điểm \(\frac{3}{2}\).
- Trên trục tung lấy điểm \( - 2\), vẽ đường thẳng vuông góc với trục tung tại điểm \( - 2\).
- Giao điểm của hai đường thẳng vừa vẽ là điểm B cần tìm.
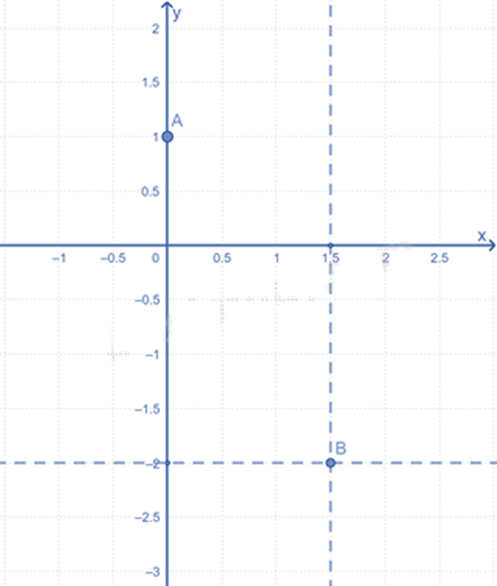
c) Điểm C nằm trên trục hoành nên có tung độ bằng 0.
Điểm C thuộc đồ thị của hàm số (1) nên ta có:
\(\begin{array}{l} - 2{x_C} + 1 = 0\\{x_C} = \frac{1}{2}\end{array}\)
Vậy tọa độ điểm C là \(C\left( {\frac{1}{2};0} \right)\).
Học sinh khối 8 ở một trường góp tiền để làm một album ca nhạc Tết Nguyên Đán 2024. Một phòng thu âm cho biết giá sản xuất đĩa gốc là 10 triệu đồng và mỗi đĩa in sao là 60 000 đồng.
a) Gọi x là số đĩa cần in sao và y là số tiền học sinh khối 8 phải trả (bao gồm tiền đĩa in sao và một đĩa gốc). Hãy biểu diễn y theo x. Hỏi y có phải là hàm số bậc nhất không? Vì sao?
b) Các bạn khối 8 cần góp bao nhiêu tiền để in được 150 đĩa sao và một đĩa gốc?
a) Dựa vào các dữ kiện đề bài cho để viết hàm số. Kiểm tra xem y có dạng \(y = ax + b\left( {a \ne 0} \right)\) không.
b) Thay x = 150 để tính số tiền.
a) Số tiền in đĩa gốc là 10 triệu đồng và số tiền in mỗi đĩa in sao là 60 000 nên nếu in x đĩa in sao và một đĩa gốc thì số tiền là: y = 60 000.x + 10 000 000
Vì hàm số y có dạng y = ax + b với a = 60 000 \( \ne \) 0 nên y là hàm số bậc nhất.
b) Để in được 150 đĩa sao và một đĩa gốc thì các bạn khối 8 cần góp số tiền là:
y = 60 000.150 + 10 000 000 = 19 000 000 (đồng)
Vậy các bạn khối 8 cần góp 19 000 000 đồng để in được 150 đĩa sao và một đĩa gốc.
Giữa hai điểm \(B\) và \(C\) bị ngăn cách bởi hồ nước (như hình dưới). Hãy xác định độ dài \(BC\) mà không cần phải bơi qua hồ. Biết rằng đoạn thẳng \(KI\) dài \(30m\) và \(K\) là trung điểm của \(AB\), \(I\) là trung điểm của \(AC\).
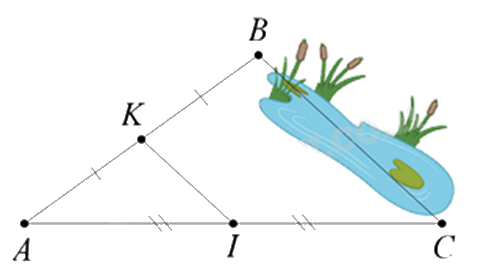
Dựa vào tính chất đường trung bình trong tam giác.
Vì K là trung điểm của AB, I là trung điểm của AC nên KI là đường trung bình của tam giác ABC
=> KI // BC và KI = \(\frac{1}{2}\)BC.
Vì KI = 30 m nên BC = 2.KI = 2.30 = 60 m.
Vậy BC = 60 m.
Cho tam giác ABC vuông tại A. Gọi O là trung điểm của AC. Trên tia BO lấy điểm D sao cho O là trung điểm của BD.
a) Chứng minh tứ giác ABCD là hình bình hành.
b) Trên tia BA lấy điểm E sao cho A là trung điểm của BE. Chứng minh rằng AC = ED.
c) Qua O kẻ OM, ON lần lượt là phân giác của các góc BOA và BOC (\(M \in AB,N \in BC\)).
Chứng minh rằng MN // AC và BO đi qua trung điểm của MN.
a) Chứng minh tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Chứng minh AO là đường trung bình của tam giác BED nên \(AO = \frac{1}{2}ED\).
Mà O là trung điểm của AC nên \(AO = \frac{1}{2}AC \Rightarrow AC = DE\).
c) Áp dụng tính chất của đường phân giác và định lí Thales đảo để chứng minh MN // AC.
Gọi F là giao điểm của BO và MN.
Dựa vào hệ quả của định lí Thales để suy ra MF = FN để được đpcm.
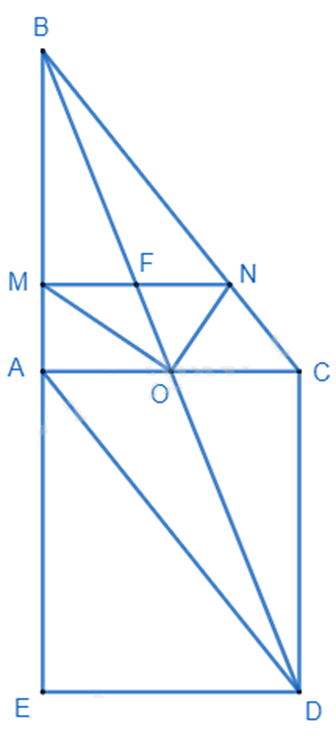
a) Xét tứ giác ABCD có:
O là trung điểm của AC
O là trung điểm của BD.
\(AC\) cắt \(BD\) tại \(O\)
\( \Rightarrow \) ABCD là hình bình hành. (đpcm)
b) Xét tam giác BED có:
A là trung điểm của BE
O là trung điểm của BD
\( \Rightarrow \) AO là đường trung bình của tam giác BED.
\( \Rightarrow AO = \frac{1}{2}ED\)
Mà \(AO = \frac{1}{2}AC\) (O là trung điểm của AC)
\( \Rightarrow AC = ED\) (đpcm)
c) Áp dụng tính chất của đường phân giác, ta có:
OM là tia phân giác của \(\widehat {AOB}\) \( \Rightarrow \frac{{AO}}{{AM}} = \frac{{OB}}{{BM}} \Rightarrow \frac{{AO}}{{OB}} = \frac{{AM}}{{BM}}\)
ON là tia phân giác của \(\widehat {BOC}\) \( \Rightarrow \frac{{OC}}{{CN}} = \frac{{OB}}{{BN}} \Rightarrow \frac{{OC}}{{OB}} = \frac{{CN}}{{BN}}\)
Mà \(AO = OC\) (gt)
\( \Rightarrow \frac{{AM}}{{BM}} = \frac{{CN}}{{BN}}\)\( \Rightarrow MN//AC\) (định lí Thales đảo) (đpcm)
Gọi F là giao điểm của MN và BO.
Vì MN // AC nên áp dụng hệ quả của định lí Thales vào:
\(\Delta AOB\) có: \(\frac{{BF}}{{BO}} = \frac{{MF}}{{AO}}\)
\(\Delta BOC\) có: \(\frac{{BF}}{{BO}} = \frac{{NF}}{{OC}}\)
\( \Rightarrow \frac{{MF}}{{AO}} = \frac{{NF}}{{OC}} \Rightarrow \frac{{MF}}{{NF}} = \frac{{AO}}{{OC}} = 1 \Rightarrow MF = NF\) hay F là trung điểm của MN \( \Rightarrow \) BO đi qua trung điểm của MN. (đpcm)
Cho đường thẳng d: y = mx + m – 1. Tìm m để d cắt Ox tại A và cắt Oy tại B sao cho tam giác AOB vuông cân.
Tìm tọa độ giao điểm của đường thẳng với hai trục tọa độ.
Tìm điều kiện để có hai tam giác cân.
Giải phương tình để tìm m.
Ta có: \(d \cap Oy = \left\{ B \right\}\)
\({x_B} = 0 \Rightarrow {y_B} = m - 1\)\( \Rightarrow B\left( {0;m - 1} \right)\)\( \Rightarrow OB = \left| {m - 1} \right|\).
\({y_A} = 0 \Leftrightarrow m{x_A} + m - 1 = 0 \Leftrightarrow {x_A} = \frac{{1 - m}}{m}\left( {m \ne 0} \right)\)\( \Rightarrow A\left( {\frac{{1 - m}}{m};0} \right)\)\( \Rightarrow OA = \left| {\frac{{1 - m}}{m}} \right|\).
Vì tam giác AOB vuông cân tại O nên:
\(\begin{array}{l}OA = OB\\\left| {m - 1} \right| = \left| {\frac{{1 - m}}{m}} \right|\\\left[ \begin{array}{l}m - 1 = \frac{{1 - m}}{m}\\m - 1 = - \frac{{1 - m}}{m}\end{array} \right.\\\left[ \begin{array}{l}{m^2} = 1\\\left( {m - 1} \right)\left( {1 - \frac{1}{m}} \right) = 0\end{array} \right.\\\left[ \begin{array}{l}m = \pm 1\\m = 1\end{array} \right.\\m = \pm 1\left( {TM} \right)\end{array}\)
Vậy \(m = \pm 1\) thì tam giác AOB vuông cân.
Đề thi giữa kì 2 Toán 8 - Đề số 2 chương trình Chân trời sáng tạo là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kì. Đề thi này không chỉ kiểm tra khả năng tính toán mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Bài viết này sẽ phân tích chi tiết cấu trúc đề thi, các dạng bài tập thường gặp và cung cấp hướng dẫn giải chi tiết để giúp học sinh ôn tập hiệu quả.
Thông thường, đề thi giữa kì 2 Toán 8 - Đề số 2 chương trình Chân trời sáng tạo sẽ bao gồm các phần sau:
Đây là một dạng bài tập cơ bản nhưng lại xuất hiện thường xuyên trong các đề thi. Để giải phương trình bậc nhất một ẩn, học sinh cần nắm vững các quy tắc biến đổi tương đương và thực hiện các phép toán một cách chính xác.
Ví dụ: Giải phương trình 2x + 3 = 7
Giải:
Tương tự như phương trình, bất phương trình bậc nhất một ẩn cũng là một dạng bài tập quan trọng. Học sinh cần nắm vững các quy tắc biến đổi tương đương và chú ý đến việc đổi dấu bất phương trình khi nhân hoặc chia cả hai vế cho một số âm.
Để giải hệ phương trình bậc nhất hai ẩn, học sinh có thể sử dụng các phương pháp như phương pháp thế hoặc phương pháp cộng đại số.
Dạng bài tập này yêu cầu học sinh phải đọc kỹ đề bài, xác định được các đại lượng liên quan và lập phương trình hoặc bất phương trình để giải quyết bài toán.
Các bài toán hình học thường yêu cầu học sinh phải vận dụng các kiến thức về tam giác, tứ giác, đường thẳng song song, đường thẳng vuông góc để chứng minh các mối quan hệ giữa các yếu tố hình học.
Đề thi giữa kì 2 Toán 8 - Đề số 2 chương trình Chân trời sáng tạo là một cơ hội để học sinh đánh giá năng lực của bản thân và chuẩn bị tốt nhất cho các kỳ thi tiếp theo. Hy vọng với những phân tích và hướng dẫn trên, các em học sinh sẽ ôn tập hiệu quả và đạt kết quả tốt nhất trong kỳ thi sắp tới.