Chào mừng các em học sinh đến với đề thi học kì 2 Toán 8 - Đề số 5, chương trình Chân trời sáng tạo. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học và hiểu rõ các dạng bài tập thường gặp. Chúc các em ôn thi tốt!
Để giải phương trình \(\frac{{2x - 3}}{4} - \frac{{1 - x}}{5} = 1\), một bạn học sinh thực hiện như sau:
Bước 1: \(\frac{{5\left( {2x - 3} \right)}}{{20}} - \frac{{4\left( {1 - x} \right)}}{{20}} = 1\)
Bước 2: \(10x - 15 - 4 + 4x = 1\)
Bước 3: \(14x - 19 = 1\)
Bước 4: \(14x = 20\)
Bước 5. \(x = \frac{{20}}{{14}} = \frac{{10}}{7}\)
Bạn học sinh thực hiện giải như vậy là:
Phương trình nào sau đây không có tập nghiệm là \(S = \left\{ 3 \right\}\)?
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
Phương trình \(2x + 7 = 3x + 15\) có tập nghiệm là
Một hộp có 5 quả bóng màu đỏ và 3 quả bóng màu xanh. Nếu bạn lấy ngẫu nhiên một quả bóng từ hộp, xác suất để lấy được quả bóng màu đỏ là bao nhiêu?
Trong trận chung kết bóng đá World Cup năm 2022 giữa hai đội Argentina và Pháp, để dự đoán kết quả, người ta bỏ cùng loại thức ăn vào hai hộp giống nhau, một hộp có gắn cờ Argentina, một hộp gắn cờ Pháp và cho Paul chọn hộp thức ăn. Người ta cho rằng nếu Paul chọn hộp gắn cờ nước nào thì đội bóng của nước đó thắng. Paul chọn ngẫu nhiên một hộp. Tính xác suất để Paul dự đoán đội Pháp thắng.
Cho $\Delta ABC\backsim \Delta DEF$ có \(\frac{{AB}}{{DE}} = \frac{1}{2}\) và diện tích \(\Delta DEF\) bằng \(160c{m^2}\). Khi đó diện tích \(\Delta ABC\) bằng:
Cho \(\Delta MNP\) có MN = 8cm, MP = 16cm. Điểm D thuộc cạnh MN sao cho ND = 2cm, điểm E thuộc cạnh MP sao cho EP = 13cm. Khi đó \(\Delta MNP\) đồng dạng với tam giác nào?
Cho hình vẽ sau, chọn câu trả lời đúng.
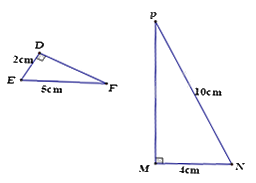
Cho hình vẽ sau, tỉ số \(\frac{{BE}}{{CE}}\) bằng
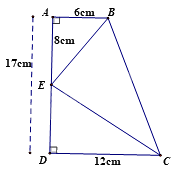
Cho các khẳng định sau:
(1) Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh.
(2) Hai hình tam giác cân bất kì luôn đồng dạng với nhau.
(3) Hai hình thoi bất kì luôn đồng dạng với nhau.
Số khẳng định đúng là:
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Giải các phương trình sau:
a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)
c) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\)
Giải bài toán bằng cách lập phương trình
Trong hội thi STEM của một trường trung học cơ sở, ban tổ chức đưa ra quy tắc chấm thi cho bài thi gồm 25 câu hỏi như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được 6 điểm, nếu trả lời không đúng thì không được điểm, nếu không trả lời thì được 1 điểm. Một học sinh làm bài thi và có số câu trả lời đúng gấp 2 lần số câu trả lời không đúng, kết quả đạt 79 điểm. Hỏi bài thi của học sinh đó có bao nhiêu câu trả lời đúng? Bao nhiêu câu trả lời không đúng? Bao nhiêu câu không trả lời?
Cho \(\Delta ABC\) có \(AB = 2cm,AC = 4cm\). Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\).
a) Chứng minh $\Delta ABD\backsim \Delta ACB$
b) Tính AD và DC.
c) Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\). Chứng minh rằng diện tích \(\Delta ABH\) gấp 4 lần diện tích \(\Delta ADE\).
Hai ban An và Bình chơi 1 ván oẳn tù tì gồm 12 lần theo luật chơi: Búa (B) thắng Kéo (K), Kéo (K) thẳng Lá (L), Lá (L) thẳng Búa (B) và hòa nhau nếu cùng loại. Sau đây là kết quả của mỗi ván chơi:

Tính xác suất thực nghiệm của biến cố “An không thắng Bình”.
Giải phương trình \(\frac{{x - 15}}{{17}} + \frac{{x - 36}}{{16}} + \frac{{x - 58}}{{14}} + \frac{{x - 76}}{{12}} = 14\).
Để giải phương trình \(\frac{{2x - 3}}{4} - \frac{{1 - x}}{5} = 1\), một bạn học sinh thực hiện như sau:
Bước 1: \(\frac{{5\left( {2x - 3} \right)}}{{20}} - \frac{{4\left( {1 - x} \right)}}{{20}} = 1\)
Bước 2: \(10x - 15 - 4 + 4x = 1\)
Bước 3: \(14x - 19 = 1\)
Bước 4: \(14x = 20\)
Bước 5. \(x = \frac{{20}}{{14}} = \frac{{10}}{7}\)
Bạn học sinh thực hiện giải như vậy là:
Đáp án : B
Dựa vào cách giải phương trình bậc nhất một ẩn để kiểm tra.
Bạn học sinh đã thực hiện sai từ bước 1, vì muốn khử mẫu thì cần quy đồng cả hai vế của phương trình mà bạn chỉ quy đồng vế trái.
Đáp án B.
Phương trình nào sau đây không có tập nghiệm là \(S = \left\{ 3 \right\}\)?
Đáp án : B
Giải các phương trình trên để xác định.
\(\begin{array}{l}3x - 9 = 0\\3x = 9\\x = 3\end{array}\)
suy ra tập nghiệm của phương trình A là \(S = \left\{ 3 \right\}\).
\(\begin{array}{l}2x + 6 = 0\\2x = - 6\\x = - 3\end{array}\)
suy ra tập nghiệm của phương trình B là \(S = \left\{ { - 3} \right\}\).
\(\begin{array}{l}2\left( {x - 1} \right) - \left( {3x - 5} \right) = 6 - 2x\\2x - 2 - 3x + 5 = 6 - 2x\\2x - 3x + 2x = 6 + 2 - 5\\x = 3\end{array}\)
suy ra tập nghiệm của phương trình C là \(S = \left\{ 3 \right\}\).
\(\frac{{x - 1}}{2} - 1 = 0\)
\(\begin{array}{l}\frac{{x - 1}}{2} - \frac{2}{2} = 0\\x - 1 - 2 = 0\\x = 3\end{array}\)
suy ra tập nghiệm của phương trình D là \(S = \left\{ 3 \right\}\).
Đáp án B.
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\left( {a \ne 0} \right)\).
Phương trình bậc nhất một ẩn là phương trình \(x + 1 = 0\).
Đáp án B.
Phương trình \(2x + 7 = 3x + 15\) có tập nghiệm là
Đáp án : A
Giải phương trình để xác định tập nghiệm
Ta có:
\(\begin{array}{l}2x + 7 = 3x + 15\\2x - 3x = 15 - 7\\ - x = 8\\x = - 8\end{array}\)
Vậy tập nghiệm của phương trình \(2x + 7 = 3x + 15\) là \(S = \left\{ { - 8} \right\}\).
Đáp án A.
Một hộp có 5 quả bóng màu đỏ và 3 quả bóng màu xanh. Nếu bạn lấy ngẫu nhiên một quả bóng từ hộp, xác suất để lấy được quả bóng màu đỏ là bao nhiêu?
Đáp án : A
Xác suất lấy được quả bóng đỏ bằng tỉ số giữa số quả bóng đỏ với tổng số quả bóng.
Có tất cả 5 + 3 = 8 quả bóng trong hộp.
Xác suất để lấy được quả bóng màu đỏ là: \(\frac{5}{8}\).
Đáp án A.
Trong trận chung kết bóng đá World Cup năm 2022 giữa hai đội Argentina và Pháp, để dự đoán kết quả, người ta bỏ cùng loại thức ăn vào hai hộp giống nhau, một hộp có gắn cờ Argentina, một hộp gắn cờ Pháp và cho Paul chọn hộp thức ăn. Người ta cho rằng nếu Paul chọn hộp gắn cờ nước nào thì đội bóng của nước đó thắng. Paul chọn ngẫu nhiên một hộp. Tính xác suất để Paul dự đoán đội Pháp thắng.
Đáp án : B
Dựa vào kiến thức về xác suất.
Vì việc Paul dự đoán đội Argentina hay Pháp thắng là hai biến cố đồng khả năng nên xác suất để Paul dự đoán đội Pháp thắng là \(\frac{1}{2}\).
Đáp án B.
Cho $\Delta ABC\backsim \Delta DEF$ có \(\frac{{AB}}{{DE}} = \frac{1}{2}\) và diện tích \(\Delta DEF\) bằng \(160c{m^2}\). Khi đó diện tích \(\Delta ABC\) bằng:
Đáp án : D
Hai tam giác đồng dạng với tỉ số k thì tỉ số diện tích của chúng bằng \({k^2}\).
Vì $\Delta ABC\backsim \Delta DEF$ có \(\frac{{AB}}{{DE}} = \frac{1}{2}\) nên tỉ số đồng dạng của \(\Delta ABC\) với \(\Delta DEF\) là \(\frac{1}{2}\).
Diện tích \(\Delta ABC\) là: \(\frac{1}{{{2^2}}}.160 = \frac{{160}}{4} = 40\left( {c{m^2}} \right)\)
Đáp án D.
Cho \(\Delta MNP\) có MN = 8cm, MP = 16cm. Điểm D thuộc cạnh MN sao cho ND = 2cm, điểm E thuộc cạnh MP sao cho EP = 13cm. Khi đó \(\Delta MNP\) đồng dạng với tam giác nào?
Đáp án : A
Dựa vào các trường hợp đồng dạng của hai tam giác.
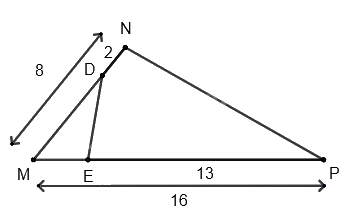
Ta có:
MD = MN – ND = 8 – 2 = 6(cm)
ME = MP – PE = 16 – 13 = 3(cm)
Xét \(\Delta MNP\) và \(\Delta MED\) có:
\(\widehat M\) chung
\(\frac{{ME}}{{MD}} = \frac{{MN}}{{MP}} = \frac{1}{2}\)
Suy ra $\Delta MNP\backsim \Delta MED$ (c.g.c)
Đáp án A.
Cho hình vẽ sau, chọn câu trả lời đúng.
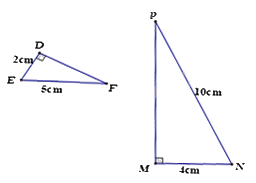
Đáp án : C
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.
Xét \(\Delta DEF\) và \(\Delta MNP\) có:
\(\begin{array}{l}\widehat D = \widehat M = {90^0}\\\frac{{DE}}{{MN}} = \frac{{EF}}{{NP}}\left( {\frac{2}{4} = \frac{5}{{10}} = \frac{1}{2}} \right)\end{array}\)
nên $\Delta DEF\backsim \Delta MNP$ (cạnh huyền – cạnh góc vuông)
Đáp án C.
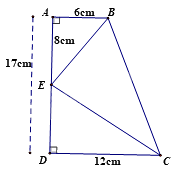
Cho hình vẽ sau, tỉ số \(\frac{{BE}}{{CE}}\) bằng
Đáp án : B
Dựa vào kiến thức về hai tam giác vuông đồng dạng để tìm tỉ số.
DE = AD – AE = 17 – 8 = 9(cm)
Xét \(\Delta ABE\) và \(\Delta DEC\) có:
\(\widehat A = \widehat D = {90^0}\)
\(\frac{{AB}}{{DE}} = \frac{{AE}}{{DC}}\left( {\frac{6}{9} = \frac{8}{{12}}\left( { = \frac{2}{3}} \right)} \right)\)
Suy ra $\Delta ABE\backsim \Delta DEC$ (hai cạnh góc vuông) suy ra \(\frac{{BE}}{{CE}} = \frac{{AB}}{{DE}} = \frac{2}{3}\)
Đáp án B.
Cho các khẳng định sau:
(1) Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh.
(2) Hai hình tam giác cân bất kì luôn đồng dạng với nhau.
(3) Hai hình thoi bất kì luôn đồng dạng với nhau.
Số khẳng định đúng là:
Đáp án : B
Dựa vào đặc điểm của các hình để xác định.
Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh nên khẳng định (1) đúng.
Hai tam giác cân bất kì luôn đồng dạng là sai vì các góc trong hai tam giác cân có thể khác nhau.
Hai hình thoi bất kì luôn đồng dạng là sai vì các góc trong hai hình thoi có thể khác nhau.
Đáp án B.
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Đáp án : D
Dựa vào bán kính hai đường tròn.
Đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng là: \(\frac{6}{3} = 2\).
Đáp án D.
Giải các phương trình sau:
a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)
c) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\)
Đưa phương trình về dạng \(ax + b = 0\) để giải.
a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
\(\begin{array}{l}7 - 2x - 4 = - x - 4\\ - 2x + x = - 4 - 7 + 4\\ - x = - 7\\x = 7\end{array}\)
Vậy \(x = 7\)
b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)
\(\begin{array}{l}\frac{{1 - 3x}}{6} + \frac{{6\left( {x - 1} \right)}}{6} = \frac{{3\left( {x + 2} \right)}}{6}\\1 - 3x + 6x - 6 = 3x + 6\\ - 3x + 6x - 3x = 6 + 6 - 1\end{array}\)
\(0 = 11\) (vô lý)
Vậy phương trình vô nghiệm.
c) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\)
\(\begin{array}{l}\frac{{8x - 3}}{4} - \frac{{x + 3}}{4} = \frac{{2x - 1}}{2} + \frac{{3x - 2}}{2}\\\frac{{8x - 3 - x - 3}}{4} = \frac{{2x - 1 + 3x - 2}}{2}\\\frac{{7x - 6}}{4} = \frac{{5x - 3}}{2}\\\frac{{7x - 6}}{4} = \frac{{2\left( {5x - 3} \right)}}{4}\\7x - 6 = 10x - 6\\7x - 10x = - 6 + 6\\ - 3x = 0\\x = 0\end{array}\)
Vậy \(x = 0\).
Giải bài toán bằng cách lập phương trình
Trong hội thi STEM của một trường trung học cơ sở, ban tổ chức đưa ra quy tắc chấm thi cho bài thi gồm 25 câu hỏi như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được 6 điểm, nếu trả lời không đúng thì không được điểm, nếu không trả lời thì được 1 điểm. Một học sinh làm bài thi và có số câu trả lời đúng gấp 2 lần số câu trả lời không đúng, kết quả đạt 79 điểm. Hỏi bài thi của học sinh đó có bao nhiêu câu trả lời đúng? Bao nhiêu câu trả lời không đúng? Bao nhiêu câu không trả lời?
Giải bài toán bằng cách lập phương trình.
Gọi số câu trả lời không đúng là x \(\left( {x \in N*,x \le 25} \right)\)
Biểu diễn số câu trả lời đúng, số câu không trả lời theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi số câu trả lời không đúng là x \(\left( {x \in N*,x \le 25} \right)\).
Vì số câu trả lời đúng gấp 2 lần số câu trả lời không đúng nên số câu trả lời đúng là \(2x\).
Số câu không trả lời là: \(25 - x - 2x = 25 - 3x\).
Vì học sinh có kết quả đạt 79 điểm nên ta có phương trình:
\(\begin{array}{l}6.2x + 1.\left( {25 - 3x} \right) + 0.x = 79\\12x + 25 - 3x = 79\\9x = 54\\x = 6\left( {TM} \right)\end{array}\)
Khi đó số câu trả lời đúng là: \(2.6 = 12\)(câu)
Số câu không trả lời là: \(25 - 3.6 = 7\)(câu)
Vậy học sinh đó trả lời đúng 12 câu, trả lời không đúng 6 câu và không trả lời 7 câu.
Cho \(\Delta ABC\) có \(AB = 2cm,AC = 4cm\). Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\).
a) Chứng minh $\Delta ABD\backsim \Delta ACB$
b) Tính AD và DC.
c) Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\). Chứng minh rằng diện tích \(\Delta ABH\) gấp 4 lần diện tích \(\Delta ADE\).
a) Chứng minh $\Delta ABD\backsim \Delta ACB$ theo trường hợp góc – góc.
b) Từ $\Delta ABD\backsim \Delta ACB$ suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra \(A{B^2} = AC.AD\), từ đó ta tính AD và DC.
c) Chứng minh $\Delta ADE\backsim \Delta ABH$ theo trường hợp góc – góc suy ra tỉ số đồng dạng giữa các cặp cạnh tương ứng để chứng minh.
Sử dụng công thức tính diện tích tam giác vuông chứng minh.
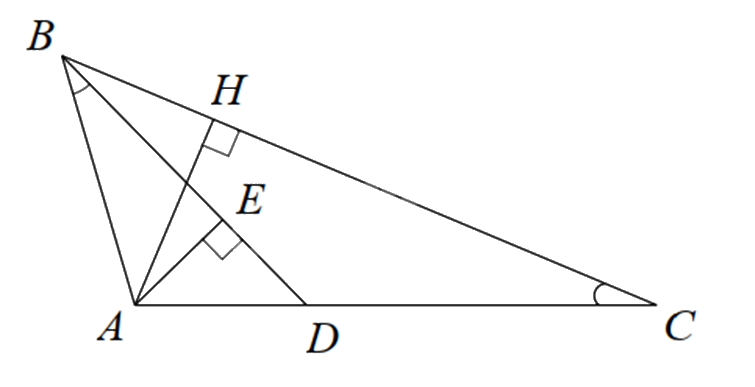
a) Xét \(\Delta ABD\) và \(\Delta ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (gt)
\(\widehat {BAC}\) chung
Suy ra $\Delta ABD\backsim \Delta ACB$ (g.g). (đpcm)
b) Vì $\Delta ABD\backsim \Delta ACB$ (cmt) suy ra \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) nên \(A{B^2} = AC.AD\).
Suy ra \({2^2} = 4.AD\) hay \(AD = 1\left( {cm} \right)\).
Suy ra \(CD = AC - AD = 4 - 1 = 3\left( {cm} \right)\)
c) Do $\Delta ABD\backsim \Delta ACB$ suy ra \(\widehat {ADE} = \widehat {ABC}\).
Xét \(\Delta AED\) và \(\Delta AHB\) có:
\(\widehat E = \widehat H = {90^0}\)
\(\widehat {ADE} = \widehat {ABC}\)(cmt)
Suy ra $\Delta ADE\backsim \Delta ABH\left( g.g \right)$ suy ra \(\frac{{AE}}{{AH}} = \frac{{DE}}{{BH}} = \frac{{AD}}{{AB}} = \frac{1}{2}\).
Do đó \(BH = 2DE;AH = 2AE\).
Từ đó suy ra \({S_{\Delta ABH}} = \frac{1}{2}BH.AH = \frac{1}{2}\left( {2DE} \right)\left( {2AE} \right) = 4.\frac{1}{2}DE.AE = 4{S_{\Delta ADE}}\) (đpcm).
Hai ban An và Bình chơi 1 ván oẳn tù tì gồm 12 lần theo luật chơi: Búa (B) thắng Kéo (K), Kéo (K) thẳng Lá (L), Lá (L) thẳng Búa (B) và hòa nhau nếu cùng loại. Sau đây là kết quả của mỗi ván chơi:

Tính xác suất thực nghiệm của biến cố “An không thắng Bình”.
Tính số lần An không thắng Bình.
Xác suất thực nghiệm của biến cố bằng tỉ số giữa tổng số lần biến cố xuất hiện với tổng số lần thực hiện biến cố.
Quan sát bảng kết quả ta thấy số lần An thắng Bình là 6 lần.
Do đó số lần An không thắng Bình là: 12 – 6 = 6 (lần)
Vậy xác suất thực nghiệm của biến cố “An không thắng Bình” là: \(\frac{6}{{12}} = \frac{1}{2}\).
Giải phương trình \(\frac{{x - 15}}{{17}} + \frac{{x - 36}}{{16}} + \frac{{x - 58}}{{14}} + \frac{{x - 76}}{{12}} = 14\).
Trừ các 2 vế cho 14 theo cách sau:
\(\left( {\frac{{x - 15}}{{17}} - 5} \right) + \left( {\frac{{x - 36}}{{16}} - 4} \right) + \left( {\frac{{x - 58}}{{14}} - 3} \right) + \left( {\frac{{x - 76}}{{12}} - 2} \right) = 0\)
Rút gọn vế trái để giải phương trình.
Trừ các 2 vế cho 14 ta được:
\(\left( {\frac{{x - 15}}{{17}} - 5} \right) + \left( {\frac{{x - 36}}{{16}} - 4} \right) + \left( {\frac{{x - 58}}{{14}} - 3} \right) + \left( {\frac{{x - 76}}{{12}} - 2} \right) = 0\)
\(\begin{array}{l}\frac{{x - 100}}{{17}} + \frac{{x - 100}}{{16}} + \frac{{x - 100}}{{14}} + \frac{{x - 100}}{{12}} = 0\\\left( {x - 100} \right)\left( {\frac{1}{{17}} + \frac{1}{{16}} + \frac{1}{{14}} + \frac{1}{{12}}} \right) = 0\\x - 100 = 0\\x = 0 + 100\\x = 100\end{array}\)
Vậy \(x = 100\)
Đề thi học kì 2 Toán 8 - Đề số 5 chương trình Chân trời sáng tạo là một công cụ quan trọng giúp học sinh đánh giá năng lực và kiến thức đã tích lũy trong suốt học kì. Đề thi bao gồm nhiều dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, đòi hỏi học sinh phải nắm vững các khái niệm, định lý và kỹ năng giải toán cơ bản.
Đề thi thường được chia thành các phần chính sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để giải phương trình bậc nhất một ẩn, ta thực hiện các bước sau:
Có hai phương pháp phổ biến để giải hệ phương trình bậc nhất hai ẩn:
Để chứng minh một tứ giác là hình bình hành, ta có thể sử dụng các tiêu chuẩn sau:
Giaitoan.edu.vn cung cấp đầy đủ đề thi học kì 2 Toán 8 - Đề số 5 chương trình Chân trời sáng tạo kèm đáp án chi tiết. Học sinh có thể tải đề thi về để luyện tập hoặc làm trực tiếp trên website để được chấm điểm tự động.
Luyện tập thường xuyên là chìa khóa để thành công trong môn Toán. Việc giải nhiều đề thi khác nhau sẽ giúp học sinh làm quen với các dạng bài tập, rèn luyện kỹ năng giải toán và tự tin hơn khi bước vào phòng thi.
Đề thi học kì 2 Toán 8 - Đề số 5 chương trình Chân trời sáng tạo là một bài kiểm tra quan trọng, đòi hỏi học sinh phải chuẩn bị kỹ lưỡng. Hy vọng với những hướng dẫn và tài liệu mà Giaitoan.edu.vn cung cấp, các em sẽ đạt kết quả tốt nhất trong kỳ thi sắp tới.