Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 10, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng.
Đề thi được biên soạn bám sát chương trình học, bao gồm các dạng bài tập đa dạng, từ cơ bản đến nâng cao, giúp học sinh làm quen với cấu trúc đề thi thực tế.
Cùng giaitoan.edu.vn chinh phục kỳ thi giữa kì 2 Toán 8 Chân trời sáng tạo một cách tự tin nhất!
Cặp đường thẳng nào sau đây song song với nhau?
\(y = - 2x + 4\) và \(y = - 2x + 4\).
\(y = x + 7\) và \(y = 7 + x\).
\(y = - 5x - 7\) và \(y = 5x - 7\).
\(y = 4x + 4\) và \(y = 4x - 5\).
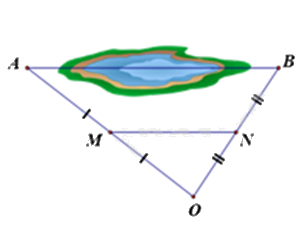
Giữa hai địa điểm A và B là một hồ nước sâu (hình bên). Biết M, N lần lượt là trung điểm của OA và OB, biết khoảng cách M và N là 300m. Tính khoảng cách AB.
600m.
1200m.
150m.
1000m.
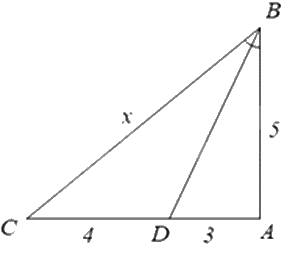
Biết BD là tia phân giác của góc B, tính giá trị của x.
\(\frac{{20}}{3}\).
\(\frac{3}{{20}}\).
\(\frac{{15}}{4}\).
\(\frac{4}{{15}}\).
Nếu $\Delta ABC\backsim \Delta A'B'C'$. theo tỉ số \(k = \frac{1}{3}\) thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số
\(\frac{1}{3}\).
\(\frac{1}{9}\).
\(3\).
\(9\).
Cho $\Delta ABC\backsim \Delta DEF$, biết \(\widehat A = 75^\circ ,\widehat B = 50^\circ \). Khi đó số đo \(\widehat F\) bằng
\(65^\circ \).
\(85^\circ \).
\(55^\circ \).
\(75^\circ \).
Cho đường thẳng \(y = 7x + 4\) và \(y = - 7x + 4\). Hai đường thẳng đã cho
cắt nhau tại điểm có hoành độ là 4.
song song với nhau.
cắt nhau tại điểm có tung độ là 4.
trùng nhau.
Đường thẳng song song với đường thẳng \(y = x\) và cắt trục tung tại điểm có tung độ bằng 1 là:
\(y = x + 1\).
\(y = - x - 1\).
\(y = x - 1\).
\(y = 3 - 2\left( {1 - x} \right)\).
Hàm số nào dưới đây là hàm số bậc nhất
\(y = 2{x^2} + \frac{1}{4}\).
\(y = \frac{{1 - 5}}{x}\).
\(y = \sqrt x - 4\).
\(y = x - 1\).
Trong các điểm sau, điểm nào thuộc đồ thị hàm số \(y = x - 1\)
\(\left( { - 1;2} \right)\).
\(\left( {2;1} \right)\).
\(\left( {2; - 1} \right)\).
\(\left( { - 2; - 1} \right)\).
Cho hàm số bậc nhất \(y = - \frac{1}{3}x + \frac{1}{3}\) có hệ số góc là:
\(3\).
\( - 3\).
\(\frac{1}{3}\).
\(\frac{{ - 1}}{3}\).
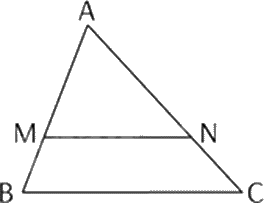
Cho tam giác ABC, biết \({\rm{MN // }}BC\). Trong khẳng định sau, khẳng định nào đúng?
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{AC}}\).
\(\frac{{AN}}{{NC}} = \frac{{MN}}{{BC}}\).
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
\(\frac{{AM}}{{MB}} = \frac{{NC}}{{AN}}\).
Cho hai đoạn thẳng \(MN = 6cm\) và \(PQ = 18\,cm\). Tỉ số của đoạn thẳng MN và PQ là:
\(\frac{2}{3}\).
\(\frac{3}{2}\).
\(\frac{1}{3}\).
\(3\).
Cho hàm số \({d_1}:y = \left( {m - 1} \right)x + 2\) với \(m \ne 1\).
a) Với \(m = 2\) thì đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) đi qua điểm \(\left( {2;4} \right)\).
b) Với \(m = - 6\) thì đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) song song với đường thẳng \({d_2}:y = - 6x - 2\).
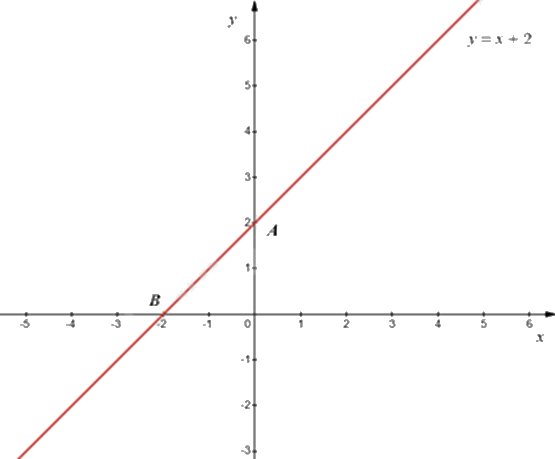
c) Đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) với \(m = 2\) được biểu diễn như sau:
d) Với \(m = - 5\) thì ba đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\), \({d_2}:y = - 6x - 2\) và \({d_3}:y = - 2x\) đồng quy.
Cho tam giác ABC, trung tuyến AM. Các tia phân giác của góc AMB, AMC cắt AB, AC lần lượt tại D và E. Cho BC = 12cm, AM = 8cm, AB = 7cm. Gọi I là giao điểm của DE và AM.
a) \(\frac{{AD}}{{DB}} = \frac{2}{3}\).
b) \(DE//BC\)
c) \(DE = \frac{{36}}{7}\).
d) \(DI = IE\)
Cho hàm số \(y = f\left( x \right) = 2x + 3\). Giá trị của \(C = 3f\left( 0 \right) - f\left( 1 \right)\) là:
Đáp án:
Cho hàm số \(y = \left( {2a - 3} \right)x - a + 3\). Giá trị a để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2 là ...
Đáp án:
Cho tam giác ABC có AB = 9 cm, điểm D thuộc cạnh AB sao AD = 6 cm. Kẻ DE song song với BC (E \( \in \) AC), kẻ EF song song với CD (F \( \in \) AB). Độ dài đoạn thẳng AF bằng bao nhiêu cm?
Đáp án:
Cho tam giác ABC có D, E lần lượt là trung điểm của các cạnh AB, AC và DE = 4cm.Biết đường cao AH = 6cm. Diện tích tam giác ABC là ...\(c{m^2}\).
Đáp án:
a) Cho hàm số \(y = f\left( x \right) = 2{x^2} + 1\). Tính \(f\left( {\frac{{ - 1}}{2}} \right)\) và \(f(1)\).
b) Cho hàm số \(y = \left( {m - 4} \right)x - 9\). Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.
c) Tìm m để các hàm số bậc nhất \(y = 3mx - 12\) (\(m \ne 0\)) và \(y = 15x + 8\) có đồ thị là những đường thẳng song song với nhau.
Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm của hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC. Chứng minh:
a) \(\Delta FBA = \Delta FCK\).
b) \(EF = \frac{{AB + CD}}{2}\).
Cặp đường thẳng nào sau đây song song với nhau?
\(y = - 2x + 4\) và \(y = - 2x + 4\).
\(y = x + 7\) và \(y = 7 + x\).
\(y = - 5x - 7\) và \(y = 5x - 7\).
\(y = 4x + 4\) và \(y = 4x - 5\).
Đáp án : D
Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song nếu \(a = a';b \ne b'\).
Đường thẳng \(y = 4x + 4\) và \(y = 4x - 5\) song song với nhau vì hệ số \(a = a';b \ne b'\).
Hai đường thẳng \(y = - 2x + 4\) và \(y = - 2x + 4\) trùng nhau vì hệ số \(a = a';b = b'\).
Hai đường thẳng \(y = x + 7\) và \(y = 7 + x\) trùng nhau vì hệ số \(a = a';b = b'\).
Hai đường thẳng \(y = - 5x - 7\) và \(y = 5x - 7\) cắt nhau vì hệ số \(a \ne a'\).
Đáp án D
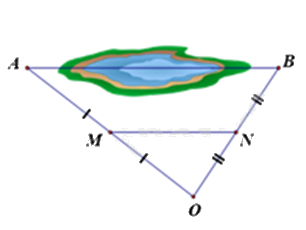
Giữa hai địa điểm A và B là một hồ nước sâu (hình bên). Biết M, N lần lượt là trung điểm của OA và OB, biết khoảng cách M và N là 300m. Tính khoảng cách AB.
600m.
1200m.
150m.
1000m.
Đáp án : A
Sử dụng tính chất của đường trung bình trong tam giác: đường trung bình bằng một nửa cạnh thứ ba.
Vì M, N lần lượt là trung điểm của OA và OB nên MN là đường trung bình của tam giác OAB, khi đó \(MN = \frac{1}{2}AB\).
Do đó khoảng cách AB là:
\(AB = 2MN = 2.300 = 600\left( m \right)\)
Đáp án A
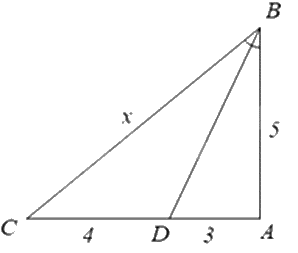
Biết BD là tia phân giác của góc B, tính giá trị của x.
\(\frac{{20}}{3}\).
\(\frac{3}{{20}}\).
\(\frac{{15}}{4}\).
\(\frac{4}{{15}}\).
Đáp án : A
Sử dụngTính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Vì BD là đường phân giác của tam giác ABC nên \(\frac{{BC}}{{BA}} = \frac{{CD}}{{DA}}\).
Thay số: \(\frac{x}{5} = \frac{4}{3}\). Suy ra \(x = \frac{4}{3}.5 = \frac{{20}}{3}\).
Đáp án A
Nếu $\Delta ABC\backsim \Delta A'B'C'$. theo tỉ số \(k = \frac{1}{3}\) thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số
\(\frac{1}{3}\).
\(\frac{1}{9}\).
\(3\).
\(9\).
Đáp án : C
Nếu $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số đồng dạng k thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng $\frac{1}{k}$.
Vì $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số \(k = \frac{1}{3}\) nên $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số \(k' = \frac{1}{k} = 1:\frac{1}{3} = 3\).
Đáp án C
Cho $\Delta ABC\backsim \Delta DEF$, biết \(\widehat A = 75^\circ ,\widehat B = 50^\circ \). Khi đó số đo \(\widehat F\) bằng
\(65^\circ \).
\(85^\circ \).
\(55^\circ \).
\(75^\circ \).
Đáp án : C
Xác định đỉnh tương ứng với đỉnh F trong tam giác ABC. Khi đó \(\widehat F\) bằng với góc ở đỉnh tương ứng của nó trong tam giác ABC.
Sử dụng định lí tổng ba góc trong một tam giác bằng \(180^\circ \) để tính góc còn lại của tam giác ABC.
Vì $\Delta ABC\backsim \Delta DEF$ nên \(\widehat F = \widehat C\).
Xét \(\Delta ABC\) có: \(\widehat A + \widehat B + \widehat C = 180^\circ \).
Suy ra \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 75^\circ - 50^\circ = 55^\circ \).
Đáp án C
Cho đường thẳng \(y = 7x + 4\) và \(y = - 7x + 4\). Hai đường thẳng đã cho
cắt nhau tại điểm có hoành độ là 4.
song song với nhau.
cắt nhau tại điểm có tung độ là 4.
trùng nhau.
Đáp án : C
Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song nếu \(a = a';b \ne b'\).
Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau nếu \(a \ne a'\).
Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) trùng nhau nếu \(a = a';b = b'\).
Đường thẳng \(y = 7x + 4\) và \(y = - 7x + 4\) có \(a \ne a'\left( {7 \ne - 7} \right)\) nên chúng cắt nhau.
Xét phương trình hoành độ giao điểm của hai đường thẳng, ta có:
\(\begin{array}{l}7x + 4 = - 7x + 4\\7x + 7x = 4 - 4\\14x = 0\\x = 0:14\\x = 0\end{array}\)
Khi đó \(y = 7.0 + 4 = 4\).
Vậy đường thẳng \(y = 7x + 4\) và \(y = - 7x + 4\) cắt nhau tại điểm có tung độ là 4.
Đáp án C
Đường thẳng song song với đường thẳng \(y = x\) và cắt trục tung tại điểm có tung độ bằng 1 là:
\(y = x + 1\).
\(y = - x - 1\).
\(y = x - 1\).
\(y = 3 - 2\left( {1 - x} \right)\).
Đáp án : D
Đường thẳng cần tìm có dạng \(y = ax + b\left( {a \ne 0} \right)\).
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song nếu \(a = a';b \ne b'\). ta tìm được hệ số a.
Vì đường thẳng cắt trục tung tại điểm có tung độ bằng 1 nên thay toạ độ giao điểm \(\left( {0;1} \right)\) vào hàm số để tìm hệ số b.
Gọi đường thẳng cần tìm có dạng \(y = ax + b\left( {a \ne 0} \right)\).
Vì đường thẳng \(y = ax + b\) song song với đường thẳng \(y = x\) nên ta có \(a = 1\).
Hàm số trở thành \(y = x + b\).
Vì đường thẳng cắt trục tung tại điểm có tung độ bằng 1 nên toạ độ giao điểm của đường thẳng và trục tung là \(\left( {0;1} \right)\). Thay \(x = 0;y = 1\) vào \(y = x + b\), ta được:
\(1 = 0 + b\) suy ra \(b = 1 - 0 = 1\).
Vậy đường thẳng cần tìm là \(y = x + 1\).
Đáp án D
Hàm số nào dưới đây là hàm số bậc nhất
\(y = 2{x^2} + \frac{1}{4}\).
\(y = \frac{{1 - 5}}{x}\).
\(y = \sqrt x - 4\).
\(y = x - 1\).
Đáp án : D
Hàm số bậc nhất là hàm số có dạng \(y = ax + b\left( {a \ne 0} \right)\) với a, b là các hệ số.
\(y = 2{x^2} + \frac{1}{4}\) không phải hàm số bậc nhất vì bậc của x là 2.
\(y = \frac{{1 - 5}}{x}\) không phải hàm số bậc nhất x ở dưới mẫu.
\(y = \sqrt x - 4\) không phải hàm số bậc nhất x nằm trong căn.
\(y = x - 1\) là hàm số bậc nhất vì có dạng \(y = ax + b\left( {a \ne 0} \right)\).
Đáp án D
Trong các điểm sau, điểm nào thuộc đồ thị hàm số \(y = x - 1\)
\(\left( { - 1;2} \right)\).
\(\left( {2;1} \right)\).
\(\left( {2; - 1} \right)\).
\(\left( { - 2; - 1} \right)\).
Đáp án : B
Thay lần lượt toạ độ của các điểm vào hàm số để kiểm tra.
Với \(x = - 1\) thì \(y = - 1 - 1 = - 2\) nên \(\left( { - 1;2} \right)\) không thuộc đồ thị hàm số \(y = x - 1\).
Với \(x = 2\) thì \(y = 2 - 1 = 1\) nên \(\left( {2;1} \right)\) thuộc đồ thị hàm số \(y = x - 1\) và \(\left( {2; - 1} \right)\)không thuộc đồ thị hàm số \(y = x - 1\).
Với \(x = - 2\) thì \(y = - 2 - 1 = - 3\) nên \(\left( { - 2; - 1} \right)\) không thuộc đồ thị hàm số \(y = x - 1\).
Đáp án B
Cho hàm số bậc nhất \(y = - \frac{1}{3}x + \frac{1}{3}\) có hệ số góc là:
\(3\).
\( - 3\).
\(\frac{1}{3}\).
\(\frac{{ - 1}}{3}\).
Đáp án : D
Hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) có a là hệ số góc.
Hệ số góc của hàm số \(y = - \frac{1}{3}x + \frac{1}{3}\) là \( - \frac{1}{3}\).
Đáp án D
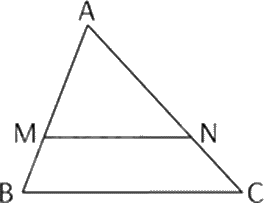
Cho tam giác ABC, biết \({\rm{MN // }}BC\). Trong khẳng định sau, khẳng định nào đúng?
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{AC}}\).
\(\frac{{AN}}{{NC}} = \frac{{MN}}{{BC}}\).
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
\(\frac{{AM}}{{MB}} = \frac{{NC}}{{AN}}\).
Đáp án : C
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Vì \({\rm{MN // }}BC\) nên \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
Đáp án C
Cho hai đoạn thẳng \(MN = 6cm\) và \(PQ = 18\,cm\). Tỉ số của đoạn thẳng MN và PQ là:
\(\frac{2}{3}\).
\(\frac{3}{2}\).
\(\frac{1}{3}\).
\(3\).
Đáp án : C
Tỉ số của đoạn thẳng MN và PQ là \(\frac{{MN}}{{PQ}}\).
Tỉ số của đoạn thẳng MN và PQ là: \(\frac{{MN}}{{PQ}} = \frac{6}{{18}} = \frac{1}{3}\).
Đáp án C
Cho hàm số \({d_1}:y = \left( {m - 1} \right)x + 2\) với \(m \ne 1\).
a) Với \(m = 2\) thì đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) đi qua điểm \(\left( {2;4} \right)\).
b) Với \(m = - 6\) thì đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) song song với đường thẳng \({d_2}:y = - 6x - 2\).
c) Đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) với \(m = 2\) được biểu diễn như sau:
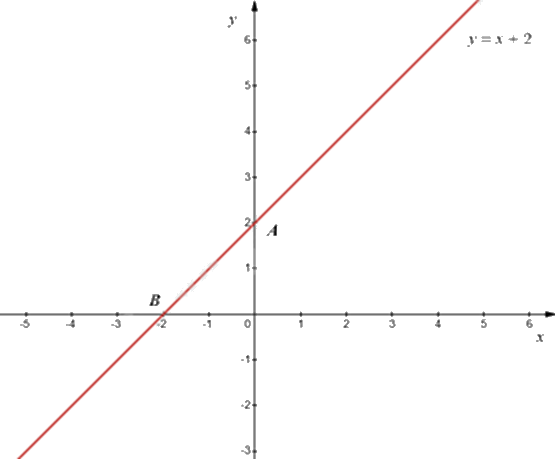
d) Với \(m = - 5\) thì ba đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\), \({d_2}:y = - 6x - 2\) và \({d_3}:y = - 2x\) đồng quy.
a) Với \(m = 2\) thì đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) đi qua điểm \(\left( {2;4} \right)\).
b) Với \(m = - 6\) thì đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) song song với đường thẳng \({d_2}:y = - 6x - 2\).
c) Đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) với \(m = 2\) được biểu diễn như sau:
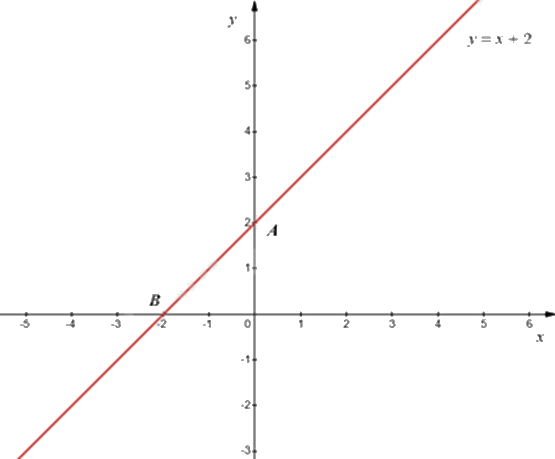
d) Với \(m = - 5\) thì ba đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\), \({d_2}:y = - 6x - 2\) và \({d_3}:y = - 2x\) đồng quy.
a) Thay \(m = 2\) vào hàm số \(y = \left( {m - 1} \right)x + 2\). Thay toạ độ điểm \(\left( {2;4} \right)\) để kiểm tra xem đường thẳng có đi qua điểm \(\left( {2;4} \right)\) không.
b) Thay \(m = - 6\) vào hàm số \(y = \left( {m - 1} \right)x + 2\).
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song nếu \(a = a';b \ne b'\).
c) Vẽ đồ thị của hàm số để kiểm tra.
d) - Tìm tọa độ giao điểm của hai đường thẳng \({d_2}:y = - 6x - 2\) và \({d_3}:y = - 2x\) theo các bước:
Bước 1: Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2: Thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số ta tìm được tung độ giao điểm.
- Để ba đường thẳng đồng quy thì giao điểm vừa tìm được thì đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) phải đi qua điểm đó.
Thay toạ độ điểm vào \(y = \left( {m - 1} \right)x + 2\) để tìm m.
a) Đúng
Thay \(m = 2\) vào hàm số \(y = \left( {m - 1} \right)x + 2\), ta được: \(y = \left( {2 - 1} \right)x + 2 = x + 2\).
Với \(x = 2\) thì \(y = 2 + 2 = 4\) nên \({d_1}:y = x + 2\) đi qua điểm \(\left( {2;4} \right)\).
b) Sai
Thay \(m = - 6\) vào hàm số \(y = \left( {m - 1} \right)x + 2\), ta được: \(y = \left( { - 6 - 1} \right)x + 2 = - 7x + 2\).
Hai đường thẳng \(y = - 7x + 2\) và \({d_2}:y = - 6x - 2\) không song song vì hệ số \( - 7 \ne - 6;2 \ne - 2\).
c) Đúng
Với \(m = 2\) thì \({d_1}\) trở thành: \(y = x + 2\).
Vẽ đường thẳng \({d_1}:x + 2\):
+) Với \(x = 0\) thì \(y = 0 + 2 = 2\) nên đồ thị hàm số đi qua điểm \(A\left( {0;2} \right)\).
+) Với \(y = 0\) thì \(x = 0 - 2 = - 2\) nên đồ thị hàm số đi qua điểm \(B\left( { - 2;0} \right)\).
Vậy đồ thị của hàm số là đường thẳng AB.
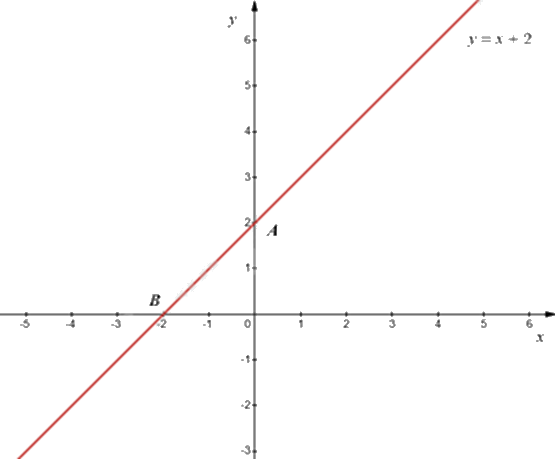
d) Sai
Xét phương trình hoành độ giao điểm của hai đường thẳng \({d_2}:y = - 6x - 2\) và \({d_3}:y = - 2x\):
\(\begin{array}{l} - 6x - 2 = - 2x\\ - 6x + 2x = 2\\ - 4x = 2\\x = \left( 2 \right):\left( { - 4} \right)\\x = \frac{{ - 1}}{2}\end{array}\)
Khi đó \(y = - 6.\frac{{ - 1}}{2} - 2 = 3 - 2 = 1\). Do đó \(\left( {\frac{{ - 1}}{2};1} \right)\) là giao điểm của hai đường thẳng \({d_2}:y = - 6x - 2\) và \({d_3}:y = - 2x\).
Để ba đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\), \({d_2}:y = - 6x - 2\) và \({d_3}:y = - 2x\) đồng quy thì đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\) cũng đi qua điểm \(\left( {\frac{1}{2}; - 1} \right)\).
Thay \(x = \frac{{ - 1}}{2};y = 1\) vào \(y = \left( {m - 1} \right)x + 2\), ta được:
\(\begin{array}{l}1 = \left( {m - 1} \right).\frac{{ - 1}}{2} + 2\\\frac{1}{2}\left( {m - 1} \right) = 2 - 1\\\frac{1}{2}\left( {m - 1} \right) = 1\\m - 1 = 1:\frac{1}{2}\\m - 1 = 2\\m = 2 + 1\\m = 3\end{array}\)
Vậy \(m = 3\) thì ba đường thẳng \({d_1}:y = \left( {m - 1} \right)x + 2\), \({d_2}:y = - 6x + 2\) và \({d_3}:y = - 2x\) đồng quy.
Đáp án: ĐSĐS
Cho tam giác ABC, trung tuyến AM. Các tia phân giác của góc AMB, AMC cắt AB, AC lần lượt tại D và E. Cho BC = 12cm, AM = 8cm, AB = 7cm. Gọi I là giao điểm của DE và AM.
a) \(\frac{{AD}}{{DB}} = \frac{2}{3}\).
b) \(DE//BC\)
c) \(DE = \frac{{36}}{7}\).
d) \(DI = IE\)
a) \(\frac{{AD}}{{DB}} = \frac{2}{3}\).
b) \(DE//BC\)
c) \(DE = \frac{{36}}{7}\).
d) \(DI = IE\)
a) Vì AM là đường trung tuyến M là trung điểm của BC. Ta tính được BM, CM theo BC.
Áp dụng tính chất của đường phân giác trong tam giác để tính \(\frac{{AD}}{{DB}}\)
b) Áp dụng tính chất của đường phân giác trong tam giác để tính được tỉ số \(\frac{{AE}}{{EC}}\).
Kết hợp với tỉ số \(\frac{{AD}}{{DB}}\) và định lí Thalès đảo để kiểm tra DE // BC.
c) Sử dụng tính chất của dãy tỉ số bằng nhau để tính AD.
Áp dụng hệ quả của định lí Thalès ta tính được DE.
d) Sử dụng hệ quả của định lí Thalès với DI // BM, IE // MC để kiểm tra DI = IE.
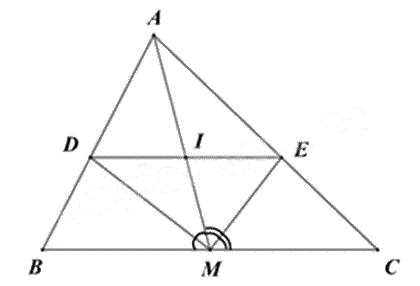
a) Sai
Vì AM là đường trung tuyến nên M là trung điểm của BC, suy ra \(BM = MC = \frac{1}{2}BC = \frac{1}{2}.12 = 6\left( {cm} \right)\). (1)
Vì MD là đường phân giác của tam giác ABM nên \(\frac{{AD}}{{DB}} = \frac{{AM}}{{BM}} = \frac{8}{6} = \frac{4}{3}\). (2)
b) Đúng
Vì ME là đường phân giác của tam giác ACM nên \(\frac{{AE}}{{EC}} = \frac{{AM}}{{MC}}\). (3)
Từ (1), (2) và (3) suy ra \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) nên DE // BC (Định lí Thalès đảo)
c) Sai
Vì \(\frac{{AD}}{{DB}} = \frac{4}{3}\) nên \(\frac{{AD}}{4} = \frac{{DB}}{3} = \frac{{AD + DB}}{{4 + 3}} = \frac{{AB}}{7} = \frac{7}{7} = 1\) (tính chất của dãy tỉ số bằng nhau)
Suy ra \(AD = 4cm,DB = 3cm\)
Áp dụng hệ quả của định lí Thalès, ta có: \(\frac{{AD}}{{AB}} = \frac{{DE}}{{BC}}\)
Suy ra \(DE = \frac{{AD}}{{AB}}.BC = \frac{4}{7}.12 = \frac{{48}}{7}\)
d) Đúng
Vì DI // BM nên \(\frac{{AI}}{{AM}} = \frac{{DI}}{{BM}}\) (hệ quả của định lí Thalès)
Vì IE // CM nên \(\frac{{AI}}{{AM}} = \frac{{IE}}{{MC}}\) (hệ quả của định lí Thalès)
Do đó \(\frac{{DI}}{{BM}} = \frac{{IE}}{{MC}}\). Mà \(BM = MC\) nên \(DI = IE\).
Đáp án: SĐSĐ
Cho hàm số \(y = f\left( x \right) = 2x + 3\). Giá trị của \(C = 3f\left( 0 \right) - f\left( 1 \right)\) là:
Đáp án:
Đáp án:
Tính \(f\left( x \right)\) tại \(x = 0,x = 1\) để tính giá trị của C.
Ta có:
\(f\left( 0 \right) = 2.0 + 3 = 3\); \(f\left( 1 \right) = 2.1 + 3 = 5\).
Suy ra \(C = 3f\left( 0 \right) - f\left( 1 \right) = 3.3 - 5 = 4\).
Đáp án: 4
Cho hàm số \(y = \left( {2a - 3} \right)x - a + 3\). Giá trị a để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2 là ...
Đáp án:
Đáp án:
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2 nên toạ độ của giao điểm là \(\left( {2;0} \right)\). Thay toạ độ giao điểm vào hàm số để tính a.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2 nên toạ độ của giao điểm là \(\left( {2;0} \right)\).
Thay \(x = 2;y = 0\) vào hàm số, ta được:
\(\begin{array}{l}0 = \left( {2a - 3} \right).2 - a + 3\\0 = 4a - 6 - a + 3\\0 = 3a - 3\\3a = 3\\a = 1\end{array}\)
Đáp án: 1
Cho tam giác ABC có AB = 9 cm, điểm D thuộc cạnh AB sao AD = 6 cm. Kẻ DE song song với BC (E \( \in \) AC), kẻ EF song song với CD (F \( \in \) AB). Độ dài đoạn thẳng AF bằng bao nhiêu cm?
Đáp án:
Đáp án:
Sử dụng hệ quả của định lí Thalès để tính tỉ số \(\frac{{AF}}{{AD}}\) theo \(\frac{{DE}}{{BC}}\): Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
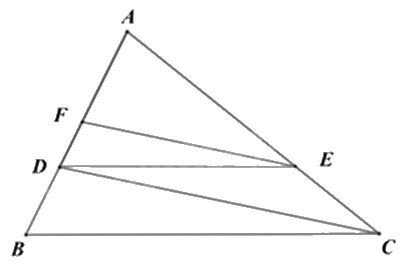
Vì DE // BC nên \(\frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{6}{9} = \frac{2}{3}\).
Vì EF // AD nên \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}} = \frac{2}{3}\)
Suy ra \(AF = \frac{2}{3}.AD = \frac{2}{3}.6 = 4\left( {cm} \right)\)
Đáp án: 4
Cho tam giác ABC có D, E lần lượt là trung điểm của các cạnh AB, AC và DE = 4cm.Biết đường cao AH = 6cm. Diện tích tam giác ABC là ...\(c{m^2}\).
Đáp án:
Đáp án:
Sử dụng tính chất đường trung bình trong tam giác và công thức tính diện tích tam giác.
- Đường trung bình của tam giác bằng một nửa cạnh thứ ba của tam giác đó.
- Diện tích tam giác = \(\frac{1}{2}\). chiều cao. đáy tương ứng.
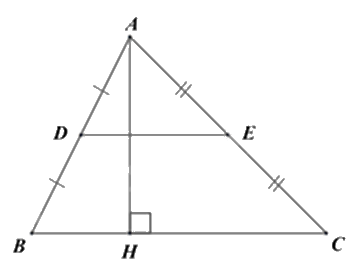
Xét tam giác ABC có D, E lần lượt là trung điểm của các cạnh AB, AC nên DE là đường trung bình của tam giác ABC. Do đó \(DE = \frac{1}{2}BC\).
Suy ra \(BC = 2.DE = 2.4 = 8\left( {cm} \right)\).
Diện tích tam giác ABC là: \({S_{\Delta ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Đáp án: 24
a) Cho hàm số \(y = f\left( x \right) = 2{x^2} + 1\). Tính \(f\left( {\frac{{ - 1}}{2}} \right)\) và \(f(1)\).
b) Cho hàm số \(y = \left( {m - 4} \right)x - 9\). Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.
c) Tìm m để các hàm số bậc nhất \(y = 3mx - 12\) (\(m \ne 0\)) và \(y = 15x + 8\) có đồ thị là những đường thẳng song song với nhau.
a) Tính \(f\left( x \right)\) tại \(x = \frac{{ - 1}}{2},x = 1\).
b) Hàm số \(y = ax + b\) là hàm số bậc nhất nếu \(a \ne 0\).
c) Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song nếu \(a = a';b \ne b'\).
a) \(f\left( {\frac{{ - 1}}{2}} \right) = 2.{\left( {\frac{{ - 1}}{2}} \right)^2} + 1 = 2.\frac{1}{4} + 1 = \frac{1}{2} + 1 = \frac{3}{2}\).
\(f\left( 1 \right) = {2.1^2} + 1 = 3\).
b) Để hàm số \(y = \left( {m - 4} \right)x - 9\) là hàm số bậc nhất thì \(m - 4 \ne 0\), suy ra \(m \ne 4\).
c) Để đồ thị hàm số \(y = 3mx - 12\) (\(m \ne 0\)) và \(y = 15x + 8\) song song với nhau thì \(3m = 15\) và \( - 12 \ne 8\).
Suy ra \(m = 15:3 = 5\) (TM điều kiện).
Vậy \(m = 5\) thì đồ thị hàm số \(y = 3mx - 12\) (\(m \ne 0\)) và \(y = 15x + 8\) song song với nhau.
Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm của hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC. Chứng minh:
a) \(\Delta FBA = \Delta FCK\).
b) \(EF = \frac{{AB + CD}}{2}\).
a) Sử dụng tính chất hai đường thẳng song song suy ra \(\widehat {ABF} = \widehat {KCF}\).
Chứng minh \(\Delta FBA = \Delta FCK\) (g.c.g)
b) Từ \(\Delta FBA = \Delta FCK\) để chứng minh AB = CK, AF = FK .
Chứng minh EF là đường trung bình của tam giác ADK.
Kết hợp với AB = CK để được điều phải chứng minh.
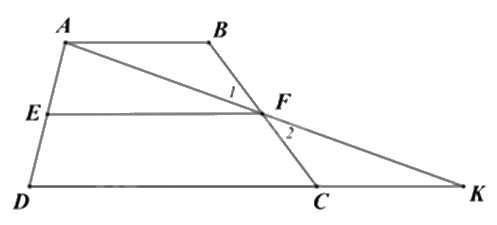
a) Vì AB // CD nên \(\widehat {ABF} = \widehat {KCF}\) (hai góc so le trong)
Xét \(\Delta FBA\) và \(\Delta FCK\) có:
\(\widehat {ABF} = \widehat {KCF}\) (cmt)
\(BF = FC\) (F là trung điểm của BC)
\(\widehat {{F_1}} = \widehat {{F_2}}\)
Suy ra \(\Delta FBA = \Delta FCK\) (g.c.g)
b) Vì \(\Delta FBA = \Delta FCK\) nên AB = CK, AF = FK (hai cặp cạnh tương ứng)
suy ra F là trung điểm của AK.
Xét tam giác ADK có E, F là trung điểm của AD, AK nên EF là đường trung bình của tam giác ADK, suy ra \(EF = \frac{{DK}}{2}\)
Mà DK = DC + CK = DC + AB (do AB = CK)
Do đó \(EF = \frac{{DC + AB}}{2}\).
Kỳ thi giữa học kỳ 2 Toán 8 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh trong nửa học kỳ vừa qua. Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 10 là một trong những đề thi được nhiều học sinh và giáo viên lựa chọn để ôn tập và kiểm tra kiến thức. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp, và hướng dẫn giải chi tiết để giúp học sinh đạt kết quả tốt nhất.
Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 10 thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 10:
Ví dụ 1: Phân tích đa thức sau thành nhân tử: x2 - 4x + 4
Giải: Ta có: x2 - 4x + 4 = (x - 2)2
Ví dụ 2: Giải phương trình sau: 2x + 5 = 11
Giải:2x = 11 - 5 => 2x = 6 => x = 3
Ví dụ 3: Cho hình chữ nhật ABCD, có AB = 8cm, BC = 6cm. Tính diện tích hình chữ nhật ABCD.
Giải: Diện tích hình chữ nhật ABCD là: S = AB * BC = 8 * 6 = 48 cm2
Học sinh có thể tham khảo các tài liệu sau để ôn thi giữa kì 2 Toán 8 Chân trời sáng tạo:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 10!