Chào mừng các em học sinh đến với đề thi học kì 1 Toán 8 - Đề số 5 chương trình Chân trời sáng tạo. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học hiệu quả và tự tin hơn trong kỳ thi sắp tới.
Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
Tính giá trị của biểu thức: 302 + 452 - 252 + 60.45 được kết quả là
Giá trị của biểu thức \(\frac{{{x^2} + 4x + 4}}{{{x^2} + 2x}}\) khi x = -2 là:
Hiệu của biểu thức \(\frac{{{\rm{x\;}} + {\rm{\;}}1{\rm{\;}}}}{{{\rm{x\;}} - {\rm{\;}}1{\rm{\;}}}}\) \(-\) \(\frac{{{\rm{x\;}}-\;4}}{{{\rm{x\;}}-{\rm{\;}}1}}\) bằng:
Cho \(\frac{{{{\left( {x + y} \right)}^2}}}{{x - y}} = \frac{P}{{{x^2} - {y^2}}}\). Đa thức P là:
Cho ABCD là hình bình hành với các điều kiện như trên hình vẽ.
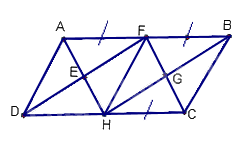
Trên hình này có:
Tứ giác là hình chữ nhật nếu:
Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm. Tính diện tích xung quanh của hình chóp.
Cho hình chóp tam giác đều S.ABC có thể tích là 100 cm3; chiều cao của hình chóp là 3cm. Độ dài cạnh đáy của hình chóp đó là (Làm tròn đến hàng đơn vị)
Độ dài một cạnh góc vuông và cạnh huyền của một tam giác vuông lần lượt là 3cm và 5cm. Diện tích của tam giác vuông đó là:
Hình bình hành ABCD là hình chữ nhật khi:
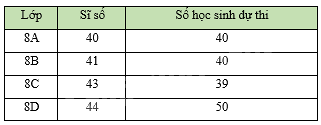
Thống kê số lượng học sinh từng lớp ở khối 8 của một trường THCS dự thi hết học kì I môn Toán. Số liệu trong bảng bên không hợp lí là:
Biểu đồ đoạn thẳng biểu diễn sô lượt người nước ngoài đến Việt Nam qua các năm 2018; 2019; 2020; 2021. (đơn vị: nghìn lượt người)
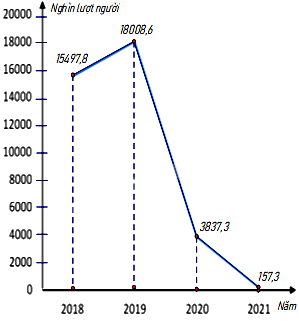
(Nguồn: Niên giám thống kê 2021)
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ đoạn thẳng ở hình bên ?
Số lượt người nước ngoài đến Việt Nam năm 2019 là bao nhiêu nghìn lượt người ?
So với năm 2018 số lượt người nước ngoài đến Việt Nam năm 2019 tăng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười) ?
Cho phân thức: \(A = \frac{{1 - 2x}}{{1 - 4{x^2}}}\)
a) Với điều kiện nào của x thì giá trị của phân thức A được xác định?
b) Rút gọn phân thức A.
c) Tính giá trị nguyên của x để phân thức A có giá trị nguyên.
a) Tìm x, biết: x2 + 3x = 0
b) Tìm giá trị nhỏ nhất của biểu thức: x2 \(-\) 4x + 7
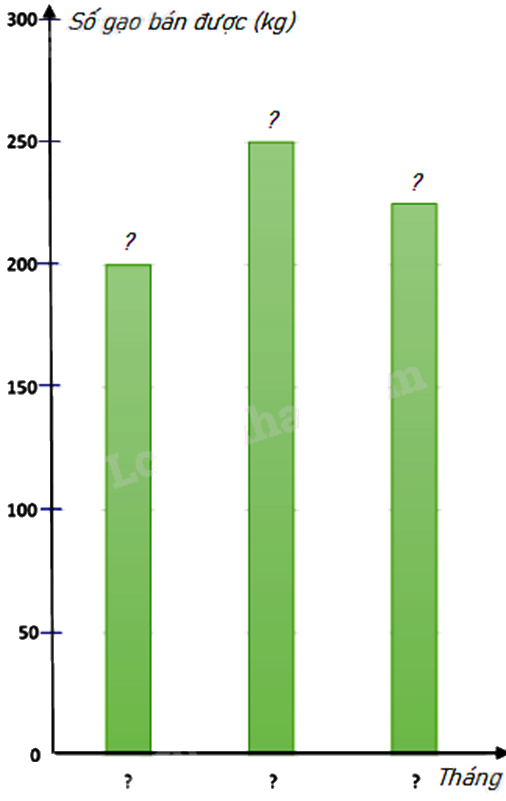
Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2022.

a) Lập bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2022 theo mẫu sau :

b) Hãy hoàn thiện biểu đồ ở hình bên dưới để nhận biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh.
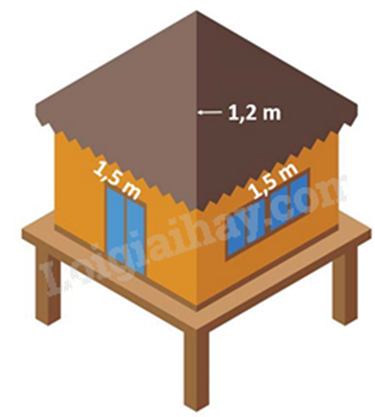
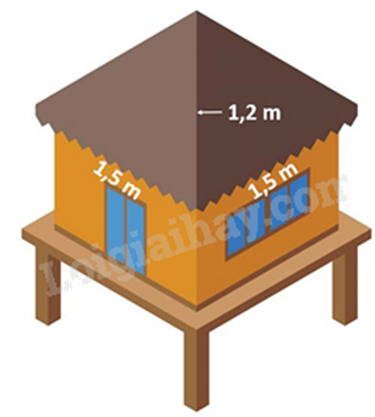
1. Mái nhà của một chòi trên bãi biển có dạng hình chóp tứ giác đều như hình bên. Tính diện tích vải bạc cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (Không tính phần viền xung quanh)
2. Cho tam giác \(ABC\) vuông tại \(A\) có \(AB < AC\). Gọi \(M\) là trung điểm của \(BC\), kẻ \(MD\) vuông góc với \(AB\) tại \(D\), \(ME\) vuông góc với \(AC\) tại \(E\).
a) Chứng minh \(AM = DE\).
b) Chứng minh tứ giác \(DMCE\) là hình bình hành.
c) Gọi \(AH\) là đường cao của tam giác \(ABC\) (\(H \in BC\)). Chứng minh tứ giác \(DHME\) là hình thang cân.
Tìm \(n \in \mathbb{N}\) để biểu thức \(A = {({n^2} + 10)^2} - 36{n^2}\) có giá trị là một số nguyên tố.
Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
Đáp án : D
- Rút gọn đa thức.
- Thay x = 73 và y = 26 vào đa thức để tính giá trị.
Ta có:
\(\begin{array}{l}{x^2} - {y^2} - 2y - 1\\ = {x^2} - \left( {{y^2} + 2y + 1} \right)\\ = {x^2} - {\left( {y + 1} \right)^2}\\ = \left( {x - y - 1} \right)\left( {x + y + 1} \right)\end{array}\)
Thay x = 73 và y = 26, ta được:
\(\left( {73 - 26 - 1} \right)\left( {73 + 26 + 1} \right) = 46.100 = 4600\).
Tính giá trị của biểu thức: 302 + 452 - 252 + 60.45 được kết quả là
Đáp án : D
Sử dụng hằng đẳng thức để tính nhanh biểu thức.
Ta có:
\(\begin{array}{l}{30^2} + {45^2} - {25^2} + 60.45\\ = {30^2} + {45^2} - {25^2} + 2.30.45\\ = \left( {{{30}^2} + 2.30.45 + {{45}^2}} \right) - {25^2}\\ = {\left( {30 + 45} \right)^2} - {25^2}\\ = {75^2} - {25^2}\\ = \left( {75 - 25} \right)\left( {75 + 25} \right)\\ = 50.100 = 5000\end{array}\)
Giá trị của biểu thức \(\frac{{{x^2} + 4x + 4}}{{{x^2} + 2x}}\) khi x = -2 là:
Đáp án : D
Kiểm tra điều kiện xác định của biểu thức. Thay x = -2 vào biểu thức.
Điều kiện xác định của biểu thức là: \({x^2} + 2x \ne 0 \Leftrightarrow x\left( {x + 2} \right) \ne 0 \Leftrightarrow \left[ \begin{array}{l}x \ne 0\\x \ne - 2\end{array} \right.\)
Vì x = -2 không thỏa mãn điều kiện xác định nên biểu thức không xác định.
Hiệu của biểu thức \(\frac{{{\rm{x\;}} + {\rm{\;}}1{\rm{\;}}}}{{{\rm{x\;}} - {\rm{\;}}1{\rm{\;}}}}\) \(-\) \(\frac{{{\rm{x\;}}-\;4}}{{{\rm{x\;}}-{\rm{\;}}1}}\) bằng:
Đáp án : A
Sử dụng quy tắc tính với phân thức đại số.
Ta có:
\(\frac{{{\rm{x\;}} + {\rm{\;}}1{\rm{\;}}}}{{{\rm{x\;}} - {\rm{\;}}1{\rm{\;}}}}\) \(-\) \(\frac{{{\rm{x\;}}-\;4}}{{{\rm{x\;}}-{\rm{\;}}1}}\)\( = \frac{{x + 1 - \left( {x - 4} \right)}}{{x - 1}} = \frac{5}{{x - 1}}\).
Cho \(\frac{{{{\left( {x + y} \right)}^2}}}{{x - y}} = \frac{P}{{{x^2} - {y^2}}}\). Đa thức P là:
Đáp án : C
Sử dụng quy tắc tính với phân thức đại số.
Ta có:
\(\frac{{{{\left( {x + y} \right)}^2}}}{{x - y}} = \frac{{{{\left( {x + y} \right)}^2}\left( {x + y} \right)}}{{\left( {x - y} \right)\left( {x + y} \right)}} = \frac{{{{\left( {x + y} \right)}^3}}}{{{x^2} - {y^2}}} = \frac{P}{{{x^2} - {y^2}}} \Rightarrow P = {\left( {x + y} \right)^3}\).
Cho ABCD là hình bình hành với các điều kiện như trên hình vẽ.
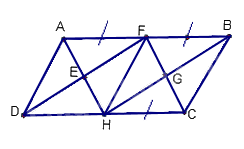
Trên hình này có:
Đáp án : D
Sử dụng kiến thức về hình bình hành.
Các hình bình hành trong hình là: ABCD; AFHD; AFCH; FBCH; FBHD; EFGH. Vậy có 6 hình bình hành.
Tứ giác là hình chữ nhật nếu:
Đáp án : D
Dựa vào kiến thức về hình chữ nhật.
Tứ giác có hai đường chéo bằng nhau có thể là hình thang cân nên A sai.
Hình thang có một góc vuông, hai góc vuông là hình thang vuông nên B, C sai.
Hình bình hành có một góc vuông là hình chữ nhật nên D đúng.
Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm. Tính diện tích xung quanh của hình chóp.
Đáp án : B
Dựa vào công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Độ dài trung đoạn là: \(\sqrt {{{25}^2} - {{\left( {\frac{{30}}{2}} \right)}^2}} = 20(cm)\)
Diện tích xung quanh của hình chóp tứ giác đều đó là:
\({S_{xq}} = \frac{{30.4}}{2}.20 = 1200\left( {c{m^2}} \right)\).
Cho hình chóp tam giác đều S.ABC có thể tích là 100 cm3; chiều cao của hình chóp là 3cm. Độ dài cạnh đáy của hình chóp đó là (Làm tròn đến hàng đơn vị)
Đáp án : C
Dựa vào công thức tính thể tích hình chóp tam giác.
Ta có thể tích hình chóp tam giác đều là: \(V = \frac{1}{3}S.h \Rightarrow S = \frac{{3V}}{h}\)
Diện tích đáy hình chóp tam giác đều là:
\(S = \frac{{3.100}}{3} = 100\left( {c{m^2}} \right)\)
Công thức tính diện tích tam giác đều là:
\(\begin{array}{l}S = \frac{{{a^2}\sqrt 3 }}{4} = 100 \Rightarrow {a^2} = 100:\frac{{\sqrt 3 }}{4} \approx 231\\ \Rightarrow a \approx 15\left( {cm} \right)\end{array}\)
Độ dài một cạnh góc vuông và cạnh huyền của một tam giác vuông lần lượt là 3cm và 5cm. Diện tích của tam giác vuông đó là:
Đáp án : C
Sử dụng định lí Pythagore để tính cạnh góc vuông còn lại.
Sử dụng công thức diện tích tam giác.
Độ dài cạnh góc vuông còn lại là: \(\sqrt {{5^2} - {3^2}} = 4\) (cm)
Diện tích của tam giác vuông đó là: \(\frac{1}{2}.3.4 = 6\left( {c{m^2}} \right)\)
Hình bình hành ABCD là hình chữ nhật khi:
Đáp án : B
Sử dụng dấu hiệu nhận biết hình chữ nhật.
Hình bình hành là hình chữ nhật nếu có hai đường chéo bằng nhau hay AC = BD.
Thống kê số lượng học sinh từng lớp ở khối 8 của một trường THCS dự thi hết học kì I môn Toán. Số liệu trong bảng bên không hợp lí là:
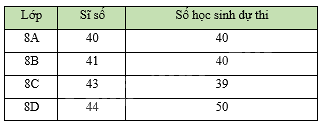
Đáp án : D
Quan sát bảng thống kê để chỉ ra dữ liệu chưa hợp lý
Quan sát bảng thống kê, ta thấy lớp 8D có sĩ số 44 học sinh nhưng số học sinh dự thi là 50 > 44 không hợp lí.
Biểu đồ đoạn thẳng biểu diễn sô lượt người nước ngoài đến Việt Nam qua các năm 2018; 2019; 2020; 2021. (đơn vị: nghìn lượt người)
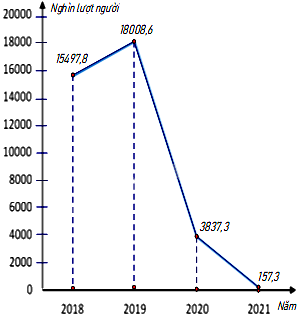
(Nguồn: Niên giám thống kê 2021)
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ đoạn thẳng ở hình bên ?
Đáp án: C
Quan sát biểu đồ để trả lời câu hỏi.
Dữ liệu trên còn có thể biểu diễn bằng biểu đồ cột.
Số lượt người nước ngoài đến Việt Nam năm 2019 là bao nhiêu nghìn lượt người ?
Đáp án: B
Quan sát biểu đồ để trả lời câu hỏi.
Số lượt người nước ngoài đến Việt Nam năm 2019 là 18008,6 nghìn lượt người.
So với năm 2018 số lượt người nước ngoài đến Việt Nam năm 2019 tăng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười) ?
Đáp án: A
Quan sát biểu đồ để trả lời câu hỏi.
Số lượt người nước ngoài đến Việt Nam năm 2018 là 15497,8 nghìn lượt người.
Số lượt người nước ngoài đến Việt Nam năm 2019 hơn năm 2018 là: 18008,6 - 15497,8 = 2510,8 (nghìn lượt người).
So với năm 2018 số lượt người nước ngoài đến Việt Nam năm 2019 tăng: \(\frac{{2510,8}}{{15497,8}}.100\% \approx 16,2\% \)
Cho phân thức: \(A = \frac{{1 - 2x}}{{1 - 4{x^2}}}\)
a) Với điều kiện nào của x thì giá trị của phân thức A được xác định?
b) Rút gọn phân thức A.
c) Tính giá trị nguyên của x để phân thức A có giá trị nguyên.
a) Điều kiện để phân thức A xác định là mẫu thức khác 0.
b) Phân tích mẫu thức thành nhân tử để rút gọn.
c) Để phân thức A nguyên thì tử thức phải chia hết cho mẫu thức.
a) Phân thức A xác định khi và chỉ khi \(1 - 4{x^2} \ne 0 \Leftrightarrow \left( {1 - 2x} \right)\left( {1 + 2x} \right) \ne 0 \Leftrightarrow \left[ \begin{array}{l}1 - 2x \ne 0\\1 + 2x \ne 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ne \frac{1}{2}\\x \ne - \frac{1}{2}\end{array} \right.\)
b) Ta có:
\(A = \frac{{1 - 2x}}{{1 - 4{x^2}}} = \frac{{\left( {1 - 2x} \right)}}{{\left( {1 - 2x} \right)\left( {1 + 2x} \right)}} = \frac{1}{{1 + 2x}}\)
c) Phân thức A có giá trị nguyên khi và chỉ khi \(\frac{1}{{1 + 2x}}\) nguyên, hay \(\left( {1 + 2x} \right) \in U\left( 1 \right) = \left\{ { \pm 1} \right\}\).
Ta có bảng giá trị sau:
1 + 2x | -1 | 1 |
x | -1 (TM) | 0 (TM) |
\(A = \frac{1}{{1 + 2x}}\) | -1 | 1 |
Vậy \(x \in \left\{ { - 1;0} \right\}\) thì phân thức A có giá trị nguyên.
a) Tìm x, biết: x2 + 3x = 0
b) Tìm giá trị nhỏ nhất của biểu thức: x2 \(-\) 4x + 7
a) Nhóm nhân tử chung để tìm x.
b) Biến đổi bằng hằng đẳng thức \({a^2} - 2ab + {b^2} = {\left( {a - b} \right)^2}\).
a) \({x^2} + 3x = 0\)
\(\begin{array}{l}x(x + 3) = 0\\\left[ \begin{array}{l}x = 0\\x + 3 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = - 3\end{array} \right.\end{array}\)
Vậy x = 0 hoặc x = -3.
b) Ta có: \({x^2} - 4x + 7 = {x^2} - 4x + 4 + 3 = {\left( {x - 2} \right)^2} + 3\)
Vì \({\left( {x - 2} \right)^2} \ge 0\) với mọi \(x \in \mathbb{R}\) nên \({\left( {x - 2} \right)^2} + 3 \ge 3\) với mọi \(x \in \mathbb{R}\).
Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức x2 \(-\) 4x + 7.
Vậy giá trị nhỏ nhất của x2 \(-\) 4x + 7 bằng 3 khi x – 2 = 0 hay x = 2.
Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2022.

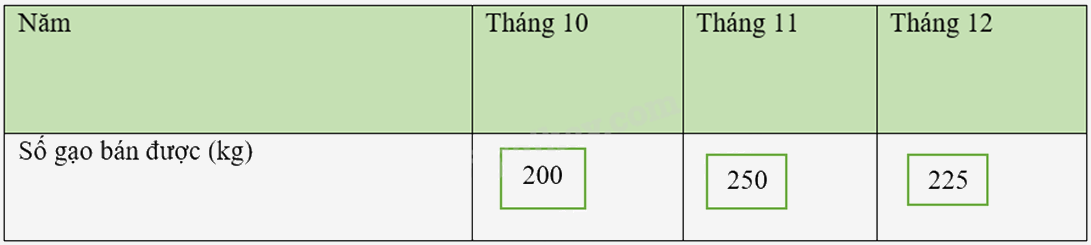
a) Lập bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2022 theo mẫu sau :

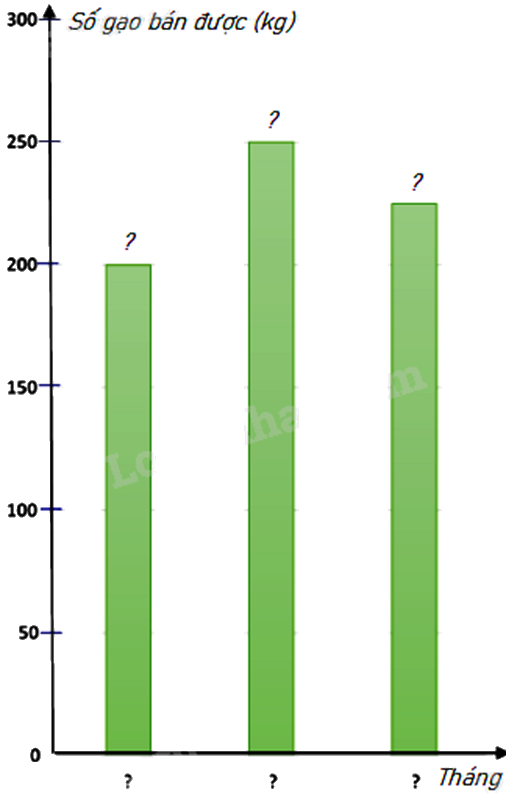
b) Hãy hoàn thiện biểu đồ ở hình bên dưới để nhận biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh.
a) Dựa vào dữ liệu đề bài cho để điền vào bảng.
b) Điền số tương ứng vào biểu đồ.
a)
b) Biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh là :
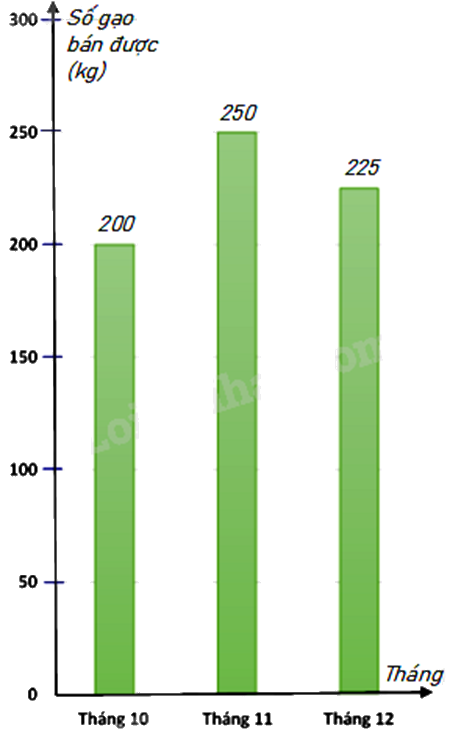
1. Mái nhà của một chòi trên bãi biển có dạng hình chóp tứ giác đều như hình bên. Tính diện tích vải bạc cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (Không tính phần viền xung quanh)
2. Cho tam giác \(ABC\) vuông tại \(A\) có \(AB < AC\). Gọi \(M\) là trung điểm của \(BC\), kẻ \(MD\) vuông góc với \(AB\) tại \(D\), \(ME\) vuông góc với \(AC\) tại \(E\).
a) Chứng minh \(AM = DE\).
b) Chứng minh tứ giác \(DMCE\) là hình bình hành.
c) Gọi \(AH\) là đường cao của tam giác \(ABC\) (\(H \in BC\)). Chứng minh tứ giác \(DHME\) là hình thang cân.
1. Sử dụng định lí Pythagore để tính độ dài trung đoạn.
Sử dụng công thức tính diện tích xung quanh hình chóp tứ giác đều để tính diện tích vải bạc cần dùng để phủ mái chòi.
2.
a) Chứng mình ADME có 3 góc vuông nên là hình chữ nhật.
b) Chứng minh \(MD\parallel EC\), \(MD = EC = \frac{1}{2}AC\) \( \Rightarrow \) đpcm.
c) \(ME = DH = AD = \frac{1}{2}AB\); \(HM\parallel DE\) nên \(DHME\) là hình thang cân.
1.
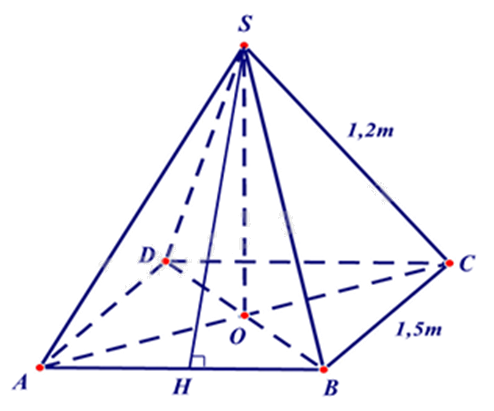
Ta có hình vẽ minh họa cho mái nhà của chòi như hình trên.
Gọi SH là đường cao của tam giác SAB nên SH là trung đoạn của hình chóp S.ABCD.
Vì S.ABCD là hình chóp tứ giác đều nên SAB là tam giác cân. Do đó SA = SB = 1,2m. Khi đó SH là đường cao đồng thời là đường trung tuyến nên AH = BH = \(\frac{1}{2}\) AB = \(\frac{1}{2}\).1,5 = 0,75(m).
Áp dụng định lí Pythagore vào tam giác vuông SHB, ta có:
\(SH = \sqrt {S{B^2} - B{H^2}} = \sqrt {1,{2^2} - 0,{{75}^2}} \approx 1\left( m \right)\)
Diện tích vải bạc cần dùng để phủ mái chòi chính là diện tích xung quanh của hình chóp tứ giác đó.
Diện tích xung quanh của hình chóp là:
\({S_{xq}} = \frac{{4.1,5}}{2}.1 = 3\left( {{m^2}} \right)\).
Vậy diện tích vải bạc cần dùng để phủ mái chòi là 3m2.
2.
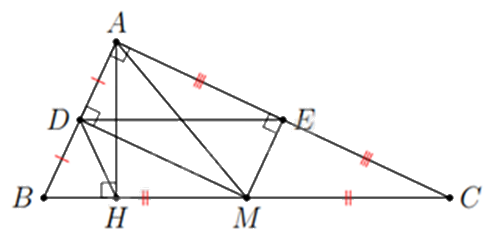
a) Xét tứ giác ADME có:
\(\widehat A = {90^0}\) (tam giác ABC vuông tại A)
\(\widehat D = \widehat E = {90^0}\) (\(MD\) vuông góc với \(AB\) tại \(D\), \(ME\) vuông góc với \(AC\) tại \(E\))
=> ADME là hình chữ nhật (tứ giác có 3 góc vuông).
b) Xét tam giác ABC vuông tại A có M là trung điểm của BC nên AM là đường trung tuyến ứng với cạnh huyền của tam giác ABC nên AM = MC = \(\frac{1}{2}\)
Khi đó tam giác AMC cân tại M. Mà ME vuông góc với AC nên ME là đường cao đồng thời là đường trung tuyến của tam giác AMC suy ra E là trung điểm của AC \( \Rightarrow \) AE = EC. (1)
ADME là hình chữ nhật nên DM // AE và DM = AE (2)
Từ (1) và (2) suy ra DM // EC và DM = EC, do đó tứ giác DMCE là hình bình hành.
c) DMCE là hình bình hành nên DE // MC => DE // HM (H thuộc đường thẳng CM)
=> DHME là hình thang.
Xét tam giác AMB có AM = BM nên tam giác AMB cân tại M. Mà MD vuông góc với AB nên MD đường cao đồng thời là đường trung tuyến của tam giác ABM suy ra D là trung điểm của AB.
Xét tam giác ABH vuông tại H, D là trung điểm của AB nên HD là đường trung tuyến ứng với cạnh huyền của tam giác AHB => \(HD = AD = \frac{1}{2}AB\).
Mà ADME là hình chữ nhật nên AD = ME suy ra HD = ME.
Hình thang DHME có HD = ME nên DHME là hình thang cân.
Tìm \(n \in \mathbb{N}\) để biểu thức \(A = {({n^2} + 10)^2} - 36{n^2}\) có giá trị là một số nguyên tố.
Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức.
Ta có: \(A = {({n^2} + 10)^2} - 36{n^2} = ({n^2} + 10 - 6n)({n^2} + 10 + 6n)\)
Để A là số nguyên tố thì A chỉ có 2 ước là 1 và chính nó.
\(A = ({n^2} + 10 - 6n)({n^2} + 10 + 6n)\) có ước là 1 và chính nó khi và chỉ khi \({n^2} + 10 - 6n = 1\) hoặc \({n^2} + 10 + 6n = 1\).
Trường hợp 1. Với \({n^2} + 10 - 6n = 1\), ta có:
\(\begin{array}{l}{n^2} + 10 - 6n = 1\\{n^2} - 6n + 9 = 0\\{\left( {n - 3} \right)^2} = 0\\n = 3\,(tm)\end{array}\)
Khi đó \(A = 1.\left( {{3^2} + 10 + 6.3} \right) = 37\)
Trường hợp 2. Với \({n^2} + 10 + 6n = 1\), ta có:
\(\begin{array}{l}{n^2} + 10 + 6n = 1\\{n^2} + 6n + 9 = 0\\{\left( {n + 3} \right)^2} = 0\end{array}\)
\(n = - 3\) (không thỏa mãn vì \(n \in \mathbb{N}\)).
Vậy n = 3 thì biểu thức \(A = {({n^2} + 10)^2} - 36{n^2}\) có giá trị là một số nguyên tố.
Đề thi học kì 1 Toán 8 - Đề số 5 chương trình Chân trời sáng tạo là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính đã được học, như biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức, hệ phương trình, và các ứng dụng thực tế của đại số.
Cấu trúc đề thi thường bao gồm các phần sau:
Các dạng bài tập thường gặp trong đề thi:
Để giúp các em học sinh ôn tập và làm quen với các dạng bài tập trong đề thi, chúng ta sẽ cùng nhau giải chi tiết một số bài tập tiêu biểu:
Lời giải:
Vậy nghiệm của phương trình là x = 2.
Lời giải:
(x + 2)(x - 2) = x2 - 22 = x2 - 4
Để đạt kết quả tốt trong kỳ thi học kì 1 Toán 8, các em học sinh nên:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu ôn tập, đề thi và bài giảng chất lượng cao. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn sẽ giúp các em học sinh học toán hiệu quả và đạt kết quả tốt nhất.
Đề thi học kì 1 Toán 8 - Đề số 5 - Chân trời sáng tạo là một cơ hội để các em học sinh thể hiện kiến thức và kỹ năng giải toán của mình. Hy vọng rằng với những hướng dẫn và lời khuyên trên, các em sẽ tự tin và đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em thành công!