Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 1 Toán 8 - Đề số 2, một công cụ hữu ích giúp các em học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 8, bao gồm các dạng bài tập thường gặp và có đáp án chi tiết đi kèm.
Với đề thi này, các em có thể tự tin làm bài và kiểm tra kiến thức đã học, đồng thời phát hiện những lỗ hổng để khắc phục kịp thời.
Câu 1: Cho các biểu thức (2x + y + {x^2}y; - 3x{y^2}{z^3} + frac{1}{2}{x^2}{y^2}z;frac{{x + y}}{{x - y}}). Có bao nhiêu đa thức trong các biểu thức trên?
Phần trắc nghiệm (3 điểm)
Câu 1: Cho các biểu thức \(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z;\frac{{x + y}}{{x - y}}\). Có bao nhiêu đa thức trong các biểu thức trên?
A. 0.
B. 1.
C. 2.
D. 3.
Câu 2: Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
A. \(14{x^2}y + 10{x^3}{y^2}\).
B. \( - 14{x^2}y + 10{x^3}{y^2}\).
C. \(6{x^2}y - 10{x^3}{y^2}\).
D. \( - 6{x^2}y + 10{x^3}{y^2}\).
Câu 3: Đơn thức thích hợp điền vào chỗ trống của ... – 9 = (5x + 3)(5x – 3) là
A. \( - 25{x^2}\).
B. \(5{x^2}\).
C. \(5x\).
D. \(25{x^2}\).
Câu 4: Biểu thức nào dưới đây là bình phương thiếu của tổng hai biểu thức x và 2y
A. \({x^2} + 2xy + 4{y^2}\).
B. \({x^2} - 2xy + 4{y^2}\).
C. \({x^2} - 4xy + 4{y^2}\).
D. \({x^2} + 4xy + 4{y^2}\).
Câu 5: Nhận xét nào sau đây đúng với hình chóp tứ giác đều
A. Thể tích bằng nửa chu vi đáy và chiều cao của hình chóp.
B. Hình chóp tứ giác đều có 1 đỉnh, 5 mặt , 8 cạnh.
C. Hình chóp tứ giác đều có 4 mặt bên là các tam giác vuông.
D. Diện tích xung quanh bằng tổng chu vi đáy và trung đoạn.
Câu 6: Tính giá trị biểu thức \(x(x - y) + y(x + y)\) tại \(x = 6\) và \(y = 8\) là
A. 14.
B. 7.
C. -100.
D. 100.
Câu 7: Một hình chóp tứ giác đều S.ABCD có độ dài trung đoạn là 12cm và đáy là hình vuông có chu vi là 40cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
A. 100cm2.
B. 120cm2.
C. 150cm2.
D. 240cm2.
Câu 8: Với giá trị nào của a thì biểu thức \({x^2} + 4x + a\) viết được dưới dạng bình phương của một tổng
A. a = 1.
B. a = 9.
C. a = 16.
D. a = 4.
Câu 9: Giá trị của biểu thức: \({x^2} - 8x + 16\) tại x = 4 là
A. 0.
B. 4.
C. -16.
D. 16.
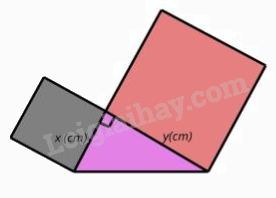
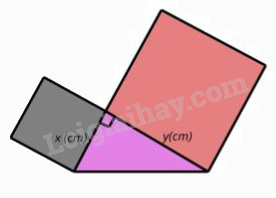
Câu 10: Trong giờ học Mỹ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là x (cm), y (cm) như hình bên. Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là
A. 41,5 cm2.
B. 40,5 cm2.
C. 44 cm2.
D. 47,2 cm2.
Câu 11: Kết quả thương của phép chia \(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2}\) là
A. 12.
B. 24.
C. 24x2y.
D. 12x2y.
Câu 12: Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy khoảng 2,2m và độ dài trung đoạn khoảng 2,8m. Cần phải trả số tiền để làm mái che giếng trời đó khi biết giá để làm mỗi mét vuông mái che được tính là 1 800 000 đồng (bao gồm tiền vật liệu và tiền công) là:

A. 22 176 000 đồng.
B. 23 176 000 đồng.
C. 21 176 000 đồng.
D. Đáp án khác.
Phần tự luận (7 điểm)
Bài 1. (2 điểm) Rút gọn rồi tính giá trị của biểu thưc
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right)\) tại \(x = \frac{{ - 1}}{2}\) và \(y = 4\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right)\) tại \(x = \frac{1}{2}\) và \(y = 2\).
Bài 2. (2 điểm)
1) Tìm x, biết:
a) \(2{x^2} + x = 0\)
b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\)
2) Tính nhanh: \({34^2} + {16^2} + 32.34\)
Bài 3. (2,5 điểm)
1.Một giá đèn cầy có dạng hình chóp tứ giác đều như hình bên có độ dài cạnh đáy là 14cm; chiều cao của giá đèn cầy là 22cm. Mặt bên của giá đèn cầy là các tam giác cân có chiều cao là 23cm. Tính diện tích xung quanh và thể tích của giá đèn cầy có dạng hình chóp tứ giác đều với kích thước như trên.

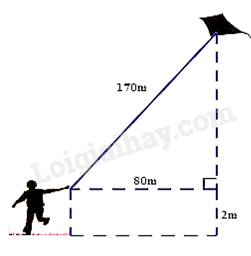
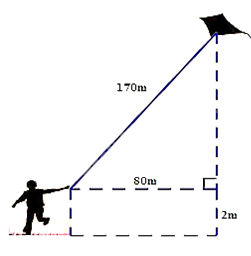
2. Một bạn học sinh thả diều ngoài đồng, cho biết đoạn dây diều từ tay bạn đến diều dài 170m và bạn đứng cách nơi diều được thả lên theo phương thẳng đứng là 80m. Tính độ cao của con diều so với mặt đất, biết tay bạn học sinh cách mặt đất 2m.
Bài 4. (0,5 điểm) Chứng minh rằng \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
-------- Hết --------
Phần trắc nghiệm (3 điểm)
1. C | 2. D | 3. D | 4. A | 5. B | 6. D |
7. D | 8. D | 9. A | 10. A | 11. B | 12. A |
Câu 1: Cho các biểu thức \(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z;\frac{{x + y}}{{x - y}}\). Có bao nhiêu đa thức trong các biểu thức trên?
A. 0. | B. 1. |
C. 2. | D. 3. |
Phương pháp
Dựa vào khái niệm đa thức: Đa thức là tổng của những đơn thức; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Lời giải
\(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z\) là những đa thức vì là tổng của những đơn thức.
\(\frac{{x + y}}{{x - y}}\) không phải đa thức.
Đáp án C.
Câu 2: Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
A. \(14{x^2}y + 10{x^3}{y^2}\). | B. \( - 14{x^2}y + 10{x^3}{y^2}\). |
C. \(6{x^2}y - 10{x^3}{y^2}\). | D. \( - 6{x^2}y + 10{x^3}{y^2}\). |
Phương pháp
Cộng, trừ các hạng tử đồng dạng để rút gọn.
Lời giải
\(\begin{array}{l}4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\\ = \left( {4{x^2}y - 10{x^2}y} \right) + \left( {6{x^3}{y^2} + 4{x^3}{y^2}} \right)\\ = - 6{x^2}y + 10{x^3}{y^2}\end{array}\)
Đáp án D.
Câu 3: Đơn thức thích hợp điền vào chỗ trống của ... – 9 = (5x + 3)(5x – 3) là
A. \( - 25{x^2}\). | B. \(5{x^2}\). |
C. \(5x\). | D. \(25{x^2}\). |
Phương pháp
Sử dụng công thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\).
Lời giải
\(\left( {5x + 3} \right)\left( {5x - 3} \right) = {\left( {5x} \right)^2} - {3^2} = 25{x^2} - 9\).
Vậy đơn thức điền vào chỗ trống là 25x2.
Đáp án D.
Câu 4: Biểu thức nào dưới đây là bình phương thiếu của tổng hai biểu thức x và 2y
A. \({x^2} + 2xy + 4{y^2}\). | B. \({x^2} - 2xy + 4{y^2}\). |
C. \({x^2} - 4xy + 4{y^2}\). | D. \({x^2} + 4xy + 4{y^2}\). |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
Bình phương thiếu của tổng hai biểu thức x và 2y là \({x^2} + 2xy + 4{y^2}\).
Đáp án A.
Câu 5: Nhận xét nào sau đây đúng với hình chóp tứ giác đềuA.Thể tích bằng nửa chu vi đáy và chiều cao của hình chóp.B. Hình chóp tứ giác đều có 1 đỉnh, 5 mặt , 8 cạnh.C.Hình chóp tứ giác đều có 4 mặt bên là các tam giác vuông.D.Diện tích xung quanh bằng tổng chu vi đáy và trung đoạn.
Phương pháp
Dựa vào kiến thức về hình chóp tứ giác đều.
Lời giải
- Thể tích của hình chóp bằng \(\frac{1}{3}\) tích của diện tích đáy và chiều cao nên A sai.
- Hình chóp tứ giác có 1 đỉnh, 5 mặt (4 mặt bên + 1 mặt đáy), 8 cạnh (4 cạnh bên và 4 cạnh đáy) nên B đúng.
- Hình chóp tứ giác đều có 4 mặt bên là các tam giác cân tại đỉnh nên C sai.
- Diện tích xung quanh hình chóp bằng tích của nửa chu vi đáy và trung đoạn nên D sai.
Đáp án B.
Câu 6: Tính giá trị biểu thức \(x(x - y) + y(x + y)\) tại \(x = 6\) và \(y = 8\) là
A. 14. | B. 7. |
C. -100. | D. 100. |
Phương pháp
Rút gọn biểu thức sau đó thay giá trị x, y vào biểu thức.
Lời giải
\(x(x - y) + y(x + y) = {x^2} - xy + xy + {y^2} = {x^2} + {y^2}\).
Thay \(x = 6\) và \(y = 8\) vào biểu thức, ta được: \({6^2} + {8^2} = 100\).
Đáp án D.
Câu 7: Một hình chóp tứ giác đều S.ABCD có độ dài trung đoạn là 12cm và đáy là hình vuông có chu vi là 40cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
A. 100cm2. | B. 120cm2. |
C. 150cm2. | D. 240cm2. |
Phương pháp
Dựa vào công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Lời giải
Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là:
\({S_{xq}} = \frac{{40}}{2}.12 = 240\)(cm2).
Đáp án D.
Câu 8: Với giá trị nào của a thì biểu thức \({x^2} + 4x + a\) viết được dưới dạng bình phương của một tổng
A. a = 1. | B. a = 9. |
C. a = 16. | D. a = 4. |
Phương pháp
Dựa vào kiến thức về hằng đẳng thức.
Lời giải
Ta có:
\(\begin{array}{l}{\left( {x + 2} \right)^2} = {x^2} + 2.2x + {2^2} = {x^2} + 4x + 4\\ \Rightarrow a = 4\end{array}\)
Đáp án D.
Câu 9: Giá trị của biểu thức: \({x^2} - 8x + 16\) tại x = 4 là
A. 0. | B. 4. |
C. -16. | D. 16. |
Phương pháp
Đưa biểu thức về bình phương của một hiệu, thay x = 4 để tính giá trị.
Lời giải
\({x^2} - 8x + 16 = {x^2} - 2.4.x + {4^2} = {\left( {x - 4} \right)^2}\).
Thay x = 4 vào biểu thức ta được: \({(4 - 4)^2} = {0^2} = 0\).
Đáp án a.
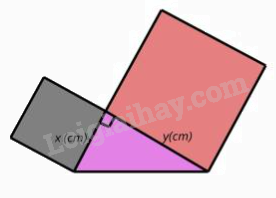
Câu 10: Trong giờ học Mỹ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là x (cm), y (cm) như hình bên. Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là
A. 41,5 cm2. | B. 40,5 cm2. |
C. 44 cm2. | D. 47,2 cm2. |
Phương pháp
Dựa vào công thức tính diện tích hình vuông, diện tích hình tam giác.
Lời giải
Diện tích hai hình vuông là: \({x^2} + {y^2} = {3^2} + {5^2} = 34\)(cm2).
Diện tích hình tam giác vuông là: \(\frac{{x.y}}{2} = \frac{{3.5}}{2} = \frac{{15}}{2} = 7,5\)(cm2).
Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là: 34 + 7,5 = 41,5 (cm2).
Đáp án A.
Câu 11: Kết quả thương của phép chia \(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2}\) là
A. 12. | B. 24. |
C. 24x2y. | D. 12x2y. |
Phương pháp
Dựa vào quy tắc chia đơn thức cho đơn thức.
Lời giải
\(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2} = 6{x^4}{y^2}:\frac{1}{4}{x^4}{y^2} = \left( {6:\frac{1}{4}} \right)\left( {{x^4}:{x^4}} \right)\left( {{y^2}:{y^2}} \right) = 24\)
Đáp án B.
Câu 12: Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy khoảng 2,2m và độ dài trung đoạn khoảng 2,8m. Cần phải trả số tiền để làm mái che giếng trời đó khi biết giá để làm mỗi mét vuông mái che được tính là 1 800 000 đồng (bao gồm tiền vật liệu và tiền công) là:

A. 22 176 000 đồng.
B. 23 176 000 đồng.
C. 21 176 000 đồng.
D. Đáp án khác.
Phương pháp
Dựa vào công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Số tiền phải trả = diện tích xung quanh . giá để làm 1 mét vuông mái che.
Lời giải
Diện tích xung quanh của mái che giếng trời có dạng hình chóp tứ giác đều đó là:
\({S_{xq}} \approx \frac{1}{2}.\left( {2,2\,.\,4} \right).2,8 = 12,32\,\left( {{m^2}} \right)\)
Số tiền cần phải trả (bao gồm tiền vật liệu và tiền công) để làm mái che giếng trời đó là:
12,32 . 1 800 000 = 22 176 000 (đồng).
Đáp án A.
Phần tự luận. (7 điểm)
Bài 1. (2 điểm) Rút gọn rồi tính giá trị của biểu thưc
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right)\) tại \(x = \frac{{ - 1}}{2}\) và \(y = 4\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right)\) tại \(x = \frac{1}{2}\) và \(y = 2\).
Phương pháp
+ Sử dụng quy tắc cộng, trừ, nhân, chia đa thức và những hằng đẳng thức đáng nhớ để rút gọn.
+ Thay x, y vào để tính giá trị.
Lời giải
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right) = {\left( {2x} \right)^2} - {\left( {\frac{1}{2}y} \right)^2} = 4{x^2} - \frac{1}{4}{y^2}\)
Thay \(x = \frac{{ - 1}}{2}\) và \(y = 4\) vào M ta được:
\(4{\left( {\frac{{ - 1}}{2}} \right)^2} - \frac{1}{4}{.4^2} = 4.\frac{1}{4} - \frac{1}{4}.16 = 1 - 4 = - 3\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right) = {\left( {2x} \right)^3} - {\left( {{y^2}} \right)^3} = 8{x^3} - {y^6}\)
Thay \(x = \frac{1}{2}\) và \(y = 2\) vào N ta được:
\(8{\left( {\frac{1}{2}} \right)^3} - {2^6} = 8.\frac{1}{8} - 64 = 1 - 64 = - 63\).
Bài 2. (2 điểm)
1) Tìm x, biết:
a) \(2{x^2} + x = 0\) | b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\) |
2) Tính nhanh: \({34^2} + {16^2} + 32.34\)
Phương pháp
1) Phân tích đa thức thành nhân tử để tìm x.
2) Dựa vào hằng đẳng thức đáng nhớ để tính.
Lời giải
1)
a) \(2{x^2} + x = 0\) \(\begin{array}{l}x(2x + 1) = 0\\\left[ \begin{array}{l}x = 0\\2x + 1 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = \frac{{ - 1}}{2}\end{array} \right.\end{array}\) Vậy \(x = 0\) hoặc \(x = \frac{{ - 1}}{2}\). | b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\) \(\begin{array}{l}x(2x - 10) - x(3 + 2x) = 26\\x(2x - 10 - 3 - 2x) = 26\\x.( - 13) = 26\\x = - 2\end{array}\) Vậy x = -2. |
2) \({34^2} + {16^2} + 32.34\) = 342 + 162 + 2.16.34 = (34 + 16)2 = 502 = 2500.
Bài 3. (2,5 điểm)
1.Một giá đèn cầy có dạng hình chóp tứ giác đều như hình bên có độ dài cạnh đáy là 14cm; chiều cao của giá đèn cầy là 22cm. Mặt bên của giá đèn cầy là các tam giác cân có chiều cao là 23cm. Tính diện tích xung quanh và thể tích của giá đèn cầy có dạng hình chóp tứ giác đều với kích thước như trên.

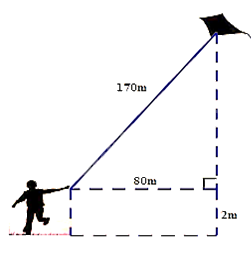
2. Một bạn học sinh thả diều ngoài đồng, cho biết đoạn dây diều từ tay bạn đến diều dài 170m và bạn đứng cách nơi diều được thả lên theo phương thẳng đứng là 80m. Tính độ cao của con diều so với mặt đất, biết tay bạn học sinh cách mặt đất 2m.
Phương pháp
1. Sử dụng công thức tính diện tích xung quanh và thể tích của hình chóp tứ giác đều.
2. Sử dụng định lí Pythagore.
Lời giải
1. Diện tích xung quanh của giá đèn cầy hình chóp tứ giác đều :
\({S_{xq}} = \frac{1}{2}.C.d = \frac{1}{2}.(4.14).23 = 644(c{m^2})\)
Thể tích của giá đèn cầy hình chóp tứ giác đều :
\(V = \frac{1}{3}.S.h = \frac{1}{3}.(14.14).22 = \frac{{4312}}{3}(c{m^3})\)
2.
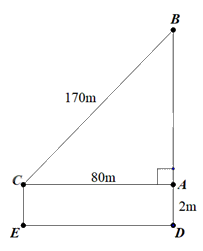
Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông tại A:
\(B{C^2} = A{B^2} + A{C^2}\)
\( \Rightarrow AB = \sqrt {{{170}^2} - {{80}^2}} = 150\)
+ Độ cao của con diều so với mặt đất 150 + 2 = 152m
Bài 4. (0,5 điểm) Chứng minh rằng \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
Phương pháp
Dựa vào hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) để chứng minh.
Lời giải
Ta có:
\(\begin{array}{l}9 - {\left( {1 + 4k} \right)^2} = {3^2} - {\left( {1 + 4k} \right)^2} = \left( {3 - 1 - 4k} \right)\left( {3 + 1 + 4k} \right)\\ = \left( {2 - 4k} \right)\left( {4 + 4k} \right) = 2.4\left( {1 - 2k} \right)\left( {1 + k} \right) = 8\left( {1 - 2k} \right)\left( {1 + k} \right) \vdots 8\,\forall k \in \mathbb{Z}\end{array}\)
Vậy \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
Tải về
Phần trắc nghiệm (3 điểm)
Câu 1: Cho các biểu thức \(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z;\frac{{x + y}}{{x - y}}\). Có bao nhiêu đa thức trong các biểu thức trên?
A. 0.
B. 1.
C. 2.
D. 3.
Câu 2: Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
A. \(14{x^2}y + 10{x^3}{y^2}\).
B. \( - 14{x^2}y + 10{x^3}{y^2}\).
C. \(6{x^2}y - 10{x^3}{y^2}\).
D. \( - 6{x^2}y + 10{x^3}{y^2}\).
Câu 3: Đơn thức thích hợp điền vào chỗ trống của ... – 9 = (5x + 3)(5x – 3) là
A. \( - 25{x^2}\).
B. \(5{x^2}\).
C. \(5x\).
D. \(25{x^2}\).
Câu 4: Biểu thức nào dưới đây là bình phương thiếu của tổng hai biểu thức x và 2y
A. \({x^2} + 2xy + 4{y^2}\).
B. \({x^2} - 2xy + 4{y^2}\).
C. \({x^2} - 4xy + 4{y^2}\).
D. \({x^2} + 4xy + 4{y^2}\).
Câu 5: Nhận xét nào sau đây đúng với hình chóp tứ giác đều
A. Thể tích bằng nửa chu vi đáy và chiều cao của hình chóp.
B. Hình chóp tứ giác đều có 1 đỉnh, 5 mặt , 8 cạnh.
C. Hình chóp tứ giác đều có 4 mặt bên là các tam giác vuông.
D. Diện tích xung quanh bằng tổng chu vi đáy và trung đoạn.
Câu 6: Tính giá trị biểu thức \(x(x - y) + y(x + y)\) tại \(x = 6\) và \(y = 8\) là
A. 14.
B. 7.
C. -100.
D. 100.
Câu 7: Một hình chóp tứ giác đều S.ABCD có độ dài trung đoạn là 12cm và đáy là hình vuông có chu vi là 40cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
A. 100cm2.
B. 120cm2.
C. 150cm2.
D. 240cm2.
Câu 8: Với giá trị nào của a thì biểu thức \({x^2} + 4x + a\) viết được dưới dạng bình phương của một tổng
A. a = 1.
B. a = 9.
C. a = 16.
D. a = 4.
Câu 9: Giá trị của biểu thức: \({x^2} - 8x + 16\) tại x = 4 là
A. 0.
B. 4.
C. -16.
D. 16.
Câu 10: Trong giờ học Mỹ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là x (cm), y (cm) như hình bên. Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là
A. 41,5 cm2.
B. 40,5 cm2.
C. 44 cm2.
D. 47,2 cm2.
Câu 11: Kết quả thương của phép chia \(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2}\) là
A. 12.
B. 24.
C. 24x2y.
D. 12x2y.
Câu 12: Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy khoảng 2,2m và độ dài trung đoạn khoảng 2,8m. Cần phải trả số tiền để làm mái che giếng trời đó khi biết giá để làm mỗi mét vuông mái che được tính là 1 800 000 đồng (bao gồm tiền vật liệu và tiền công) là:

A. 22 176 000 đồng.
B. 23 176 000 đồng.
C. 21 176 000 đồng.
D. Đáp án khác.
Phần tự luận (7 điểm)
Bài 1. (2 điểm) Rút gọn rồi tính giá trị của biểu thưc
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right)\) tại \(x = \frac{{ - 1}}{2}\) và \(y = 4\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right)\) tại \(x = \frac{1}{2}\) và \(y = 2\).
Bài 2. (2 điểm)
1) Tìm x, biết:
a) \(2{x^2} + x = 0\)
b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\)
2) Tính nhanh: \({34^2} + {16^2} + 32.34\)
Bài 3. (2,5 điểm)
1.Một giá đèn cầy có dạng hình chóp tứ giác đều như hình bên có độ dài cạnh đáy là 14cm; chiều cao của giá đèn cầy là 22cm. Mặt bên của giá đèn cầy là các tam giác cân có chiều cao là 23cm. Tính diện tích xung quanh và thể tích của giá đèn cầy có dạng hình chóp tứ giác đều với kích thước như trên.

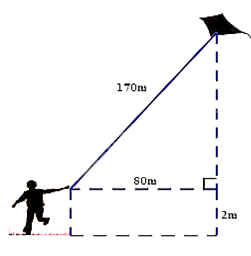
2. Một bạn học sinh thả diều ngoài đồng, cho biết đoạn dây diều từ tay bạn đến diều dài 170m và bạn đứng cách nơi diều được thả lên theo phương thẳng đứng là 80m. Tính độ cao của con diều so với mặt đất, biết tay bạn học sinh cách mặt đất 2m.
Bài 4. (0,5 điểm) Chứng minh rằng \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
-------- Hết --------
Phần trắc nghiệm (3 điểm)
1. C | 2. D | 3. D | 4. A | 5. B | 6. D |
7. D | 8. D | 9. A | 10. A | 11. B | 12. A |
Câu 1: Cho các biểu thức \(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z;\frac{{x + y}}{{x - y}}\). Có bao nhiêu đa thức trong các biểu thức trên?
A. 0. | B. 1. |
C. 2. | D. 3. |
Phương pháp
Dựa vào khái niệm đa thức: Đa thức là tổng của những đơn thức; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Lời giải
\(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z\) là những đa thức vì là tổng của những đơn thức.
\(\frac{{x + y}}{{x - y}}\) không phải đa thức.
Đáp án C.
Câu 2: Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
A. \(14{x^2}y + 10{x^3}{y^2}\). | B. \( - 14{x^2}y + 10{x^3}{y^2}\). |
C. \(6{x^2}y - 10{x^3}{y^2}\). | D. \( - 6{x^2}y + 10{x^3}{y^2}\). |
Phương pháp
Cộng, trừ các hạng tử đồng dạng để rút gọn.
Lời giải
\(\begin{array}{l}4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\\ = \left( {4{x^2}y - 10{x^2}y} \right) + \left( {6{x^3}{y^2} + 4{x^3}{y^2}} \right)\\ = - 6{x^2}y + 10{x^3}{y^2}\end{array}\)
Đáp án D.
Câu 3: Đơn thức thích hợp điền vào chỗ trống của ... – 9 = (5x + 3)(5x – 3) là
A. \( - 25{x^2}\). | B. \(5{x^2}\). |
C. \(5x\). | D. \(25{x^2}\). |
Phương pháp
Sử dụng công thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\).
Lời giải
\(\left( {5x + 3} \right)\left( {5x - 3} \right) = {\left( {5x} \right)^2} - {3^2} = 25{x^2} - 9\).
Vậy đơn thức điền vào chỗ trống là 25x2.
Đáp án D.
Câu 4: Biểu thức nào dưới đây là bình phương thiếu của tổng hai biểu thức x và 2y
A. \({x^2} + 2xy + 4{y^2}\). | B. \({x^2} - 2xy + 4{y^2}\). |
C. \({x^2} - 4xy + 4{y^2}\). | D. \({x^2} + 4xy + 4{y^2}\). |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
Bình phương thiếu của tổng hai biểu thức x và 2y là \({x^2} + 2xy + 4{y^2}\).
Đáp án A.
Câu 5: Nhận xét nào sau đây đúng với hình chóp tứ giác đềuA.Thể tích bằng nửa chu vi đáy và chiều cao của hình chóp.B. Hình chóp tứ giác đều có 1 đỉnh, 5 mặt , 8 cạnh.C.Hình chóp tứ giác đều có 4 mặt bên là các tam giác vuông.D.Diện tích xung quanh bằng tổng chu vi đáy và trung đoạn.
Phương pháp
Dựa vào kiến thức về hình chóp tứ giác đều.
Lời giải
- Thể tích của hình chóp bằng \(\frac{1}{3}\) tích của diện tích đáy và chiều cao nên A sai.
- Hình chóp tứ giác có 1 đỉnh, 5 mặt (4 mặt bên + 1 mặt đáy), 8 cạnh (4 cạnh bên và 4 cạnh đáy) nên B đúng.
- Hình chóp tứ giác đều có 4 mặt bên là các tam giác cân tại đỉnh nên C sai.
- Diện tích xung quanh hình chóp bằng tích của nửa chu vi đáy và trung đoạn nên D sai.
Đáp án B.
Câu 6: Tính giá trị biểu thức \(x(x - y) + y(x + y)\) tại \(x = 6\) và \(y = 8\) là
A. 14. | B. 7. |
C. -100. | D. 100. |
Phương pháp
Rút gọn biểu thức sau đó thay giá trị x, y vào biểu thức.
Lời giải
\(x(x - y) + y(x + y) = {x^2} - xy + xy + {y^2} = {x^2} + {y^2}\).
Thay \(x = 6\) và \(y = 8\) vào biểu thức, ta được: \({6^2} + {8^2} = 100\).
Đáp án D.
Câu 7: Một hình chóp tứ giác đều S.ABCD có độ dài trung đoạn là 12cm và đáy là hình vuông có chu vi là 40cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
A. 100cm2. | B. 120cm2. |
C. 150cm2. | D. 240cm2. |
Phương pháp
Dựa vào công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Lời giải
Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là:
\({S_{xq}} = \frac{{40}}{2}.12 = 240\)(cm2).
Đáp án D.
Câu 8: Với giá trị nào của a thì biểu thức \({x^2} + 4x + a\) viết được dưới dạng bình phương của một tổng
A. a = 1. | B. a = 9. |
C. a = 16. | D. a = 4. |
Phương pháp
Dựa vào kiến thức về hằng đẳng thức.
Lời giải
Ta có:
\(\begin{array}{l}{\left( {x + 2} \right)^2} = {x^2} + 2.2x + {2^2} = {x^2} + 4x + 4\\ \Rightarrow a = 4\end{array}\)
Đáp án D.
Câu 9: Giá trị của biểu thức: \({x^2} - 8x + 16\) tại x = 4 là
A. 0. | B. 4. |
C. -16. | D. 16. |
Phương pháp
Đưa biểu thức về bình phương của một hiệu, thay x = 4 để tính giá trị.
Lời giải
\({x^2} - 8x + 16 = {x^2} - 2.4.x + {4^2} = {\left( {x - 4} \right)^2}\).
Thay x = 4 vào biểu thức ta được: \({(4 - 4)^2} = {0^2} = 0\).
Đáp án a.
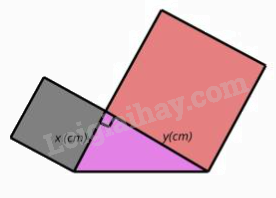
Câu 10: Trong giờ học Mỹ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là x (cm), y (cm) như hình bên. Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là
A. 41,5 cm2. | B. 40,5 cm2. |
C. 44 cm2. | D. 47,2 cm2. |
Phương pháp
Dựa vào công thức tính diện tích hình vuông, diện tích hình tam giác.
Lời giải
Diện tích hai hình vuông là: \({x^2} + {y^2} = {3^2} + {5^2} = 34\)(cm2).
Diện tích hình tam giác vuông là: \(\frac{{x.y}}{2} = \frac{{3.5}}{2} = \frac{{15}}{2} = 7,5\)(cm2).
Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là: 34 + 7,5 = 41,5 (cm2).
Đáp án A.
Câu 11: Kết quả thương của phép chia \(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2}\) là
A. 12. | B. 24. |
C. 24x2y. | D. 12x2y. |
Phương pháp
Dựa vào quy tắc chia đơn thức cho đơn thức.
Lời giải
\(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2} = 6{x^4}{y^2}:\frac{1}{4}{x^4}{y^2} = \left( {6:\frac{1}{4}} \right)\left( {{x^4}:{x^4}} \right)\left( {{y^2}:{y^2}} \right) = 24\)
Đáp án B.
Câu 12: Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy khoảng 2,2m và độ dài trung đoạn khoảng 2,8m. Cần phải trả số tiền để làm mái che giếng trời đó khi biết giá để làm mỗi mét vuông mái che được tính là 1 800 000 đồng (bao gồm tiền vật liệu và tiền công) là:

A. 22 176 000 đồng.
B. 23 176 000 đồng.
C. 21 176 000 đồng.
D. Đáp án khác.
Phương pháp
Dựa vào công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Số tiền phải trả = diện tích xung quanh . giá để làm 1 mét vuông mái che.
Lời giải
Diện tích xung quanh của mái che giếng trời có dạng hình chóp tứ giác đều đó là:
\({S_{xq}} \approx \frac{1}{2}.\left( {2,2\,.\,4} \right).2,8 = 12,32\,\left( {{m^2}} \right)\)
Số tiền cần phải trả (bao gồm tiền vật liệu và tiền công) để làm mái che giếng trời đó là:
12,32 . 1 800 000 = 22 176 000 (đồng).
Đáp án A.
Phần tự luận. (7 điểm)
Bài 1. (2 điểm) Rút gọn rồi tính giá trị của biểu thưc
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right)\) tại \(x = \frac{{ - 1}}{2}\) và \(y = 4\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right)\) tại \(x = \frac{1}{2}\) và \(y = 2\).
Phương pháp
+ Sử dụng quy tắc cộng, trừ, nhân, chia đa thức và những hằng đẳng thức đáng nhớ để rút gọn.
+ Thay x, y vào để tính giá trị.
Lời giải
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right) = {\left( {2x} \right)^2} - {\left( {\frac{1}{2}y} \right)^2} = 4{x^2} - \frac{1}{4}{y^2}\)
Thay \(x = \frac{{ - 1}}{2}\) và \(y = 4\) vào M ta được:
\(4{\left( {\frac{{ - 1}}{2}} \right)^2} - \frac{1}{4}{.4^2} = 4.\frac{1}{4} - \frac{1}{4}.16 = 1 - 4 = - 3\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right) = {\left( {2x} \right)^3} - {\left( {{y^2}} \right)^3} = 8{x^3} - {y^6}\)
Thay \(x = \frac{1}{2}\) và \(y = 2\) vào N ta được:
\(8{\left( {\frac{1}{2}} \right)^3} - {2^6} = 8.\frac{1}{8} - 64 = 1 - 64 = - 63\).
Bài 2. (2 điểm)
1) Tìm x, biết:
a) \(2{x^2} + x = 0\) | b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\) |
2) Tính nhanh: \({34^2} + {16^2} + 32.34\)
Phương pháp
1) Phân tích đa thức thành nhân tử để tìm x.
2) Dựa vào hằng đẳng thức đáng nhớ để tính.
Lời giải
1)
a) \(2{x^2} + x = 0\) \(\begin{array}{l}x(2x + 1) = 0\\\left[ \begin{array}{l}x = 0\\2x + 1 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = \frac{{ - 1}}{2}\end{array} \right.\end{array}\) Vậy \(x = 0\) hoặc \(x = \frac{{ - 1}}{2}\). | b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\) \(\begin{array}{l}x(2x - 10) - x(3 + 2x) = 26\\x(2x - 10 - 3 - 2x) = 26\\x.( - 13) = 26\\x = - 2\end{array}\) Vậy x = -2. |
2) \({34^2} + {16^2} + 32.34\) = 342 + 162 + 2.16.34 = (34 + 16)2 = 502 = 2500.
Bài 3. (2,5 điểm)
1.Một giá đèn cầy có dạng hình chóp tứ giác đều như hình bên có độ dài cạnh đáy là 14cm; chiều cao của giá đèn cầy là 22cm. Mặt bên của giá đèn cầy là các tam giác cân có chiều cao là 23cm. Tính diện tích xung quanh và thể tích của giá đèn cầy có dạng hình chóp tứ giác đều với kích thước như trên.

2. Một bạn học sinh thả diều ngoài đồng, cho biết đoạn dây diều từ tay bạn đến diều dài 170m và bạn đứng cách nơi diều được thả lên theo phương thẳng đứng là 80m. Tính độ cao của con diều so với mặt đất, biết tay bạn học sinh cách mặt đất 2m.
Phương pháp
1. Sử dụng công thức tính diện tích xung quanh và thể tích của hình chóp tứ giác đều.
2. Sử dụng định lí Pythagore.
Lời giải
1. Diện tích xung quanh của giá đèn cầy hình chóp tứ giác đều :
\({S_{xq}} = \frac{1}{2}.C.d = \frac{1}{2}.(4.14).23 = 644(c{m^2})\)
Thể tích của giá đèn cầy hình chóp tứ giác đều :
\(V = \frac{1}{3}.S.h = \frac{1}{3}.(14.14).22 = \frac{{4312}}{3}(c{m^3})\)
2.
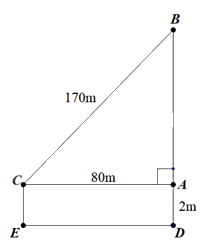
Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông tại A:
\(B{C^2} = A{B^2} + A{C^2}\)
\( \Rightarrow AB = \sqrt {{{170}^2} - {{80}^2}} = 150\)
+ Độ cao của con diều so với mặt đất 150 + 2 = 152m
Bài 4. (0,5 điểm) Chứng minh rằng \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
Phương pháp
Dựa vào hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) để chứng minh.
Lời giải
Ta có:
\(\begin{array}{l}9 - {\left( {1 + 4k} \right)^2} = {3^2} - {\left( {1 + 4k} \right)^2} = \left( {3 - 1 - 4k} \right)\left( {3 + 1 + 4k} \right)\\ = \left( {2 - 4k} \right)\left( {4 + 4k} \right) = 2.4\left( {1 - 2k} \right)\left( {1 + k} \right) = 8\left( {1 - 2k} \right)\left( {1 + k} \right) \vdots 8\,\forall k \in \mathbb{Z}\end{array}\)
Vậy \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
Đề thi giữa kì 1 Toán 8 - Đề số 2 là một bài kiểm tra đánh giá kiến thức và kỹ năng giải toán của học sinh sau một nửa học kỳ đầu tiên của lớp 8. Đề thi thường bao gồm các chủ đề chính như:
Cấu trúc đề thi thường bao gồm các dạng bài tập khác nhau như trắc nghiệm, tự luận, bài tập thực tế. Tỷ lệ phân bổ điểm cho từng phần có thể khác nhau tùy theo chương trình học của từng trường.
Trong phần đại số, học sinh cần nắm vững các kiến thức về:
Các bài tập thường gặp bao gồm:
Phần hình học yêu cầu học sinh hiểu rõ về các loại tứ giác, các tính chất và dấu hiệu nhận biết. Các bài tập thường gặp bao gồm:
Học sinh cần nắm vững kiến thức về đồ thị hàm số bậc nhất và ứng dụng của hàm số trong giải toán. Các bài tập thường gặp bao gồm:
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 8, học sinh cần:
Ngoài việc giải đề thi giữa kì 1 Toán 8 - Đề số 2, học sinh có thể tham khảo thêm các tài liệu ôn tập hữu ích sau:
Hãy dành thời gian ôn tập và luyện tập đầy đủ trước kỳ thi. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn trong quá trình học tập. Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi giữa kì 1 Toán 8!