Giaitoan.edu.vn xin giới thiệu Đề thi học kì 2 Toán 8 Chân trời sáng tạo - Đề số 6, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực trước kỳ thi quan trọng. Đề thi được biên soạn bám sát chương trình học, đảm bảo tính chính xác và cập nhật.
Với cấu trúc đề thi đa dạng, bao gồm các dạng bài tập khác nhau, học sinh có thể rèn luyện kỹ năng giải quyết vấn đề và áp dụng kiến thức đã học vào thực tế.
Đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là một đường thẳng luôn đi qua
gốc toạ độ \(O\left( {0;0} \right)\).
điểm \(A\left( {1;0} \right)\).
điểm \(B\left( {0;1} \right)\).
điểm \(C\left( {1;1} \right)\).
Hệ số góc của đường thẳng \(y = x - 2\) là:
-2.
2.
-1.
1.
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
\(0x + 5 = 0\).
\(2{x^2} - 3 = 0\).
\(\frac{3}{x} - 2 = 0\).
\(2x + 1 = 0\).
Phương trình \(3 - 2x = 0\) có nghiệm là:
\(x = 3\).
\(x = \frac{2}{3}\).
\(x = \frac{3}{2}\).
\(x = \frac{{ - 3}}{2}\).
Cho hình vẽ sau:
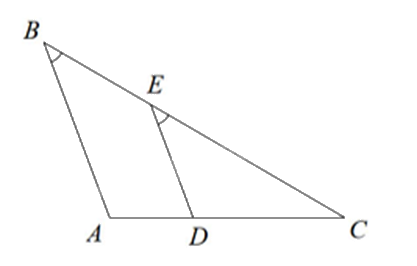
Hệ thức theo Định lí Thalès của hình trên là:
\(\frac{{CE}}{{CB}} = \frac{{CD}}{{CA}}\).
\(\frac{{BE}}{{CB}} = \frac{{CA}}{{AD}}\).
\(\frac{{CE}}{{BE}} = \frac{{AD}}{{CD}}\).
\(\frac{{DE}}{{AB}} = \frac{{AC}}{{AD}}\).
Cho các hình sau:
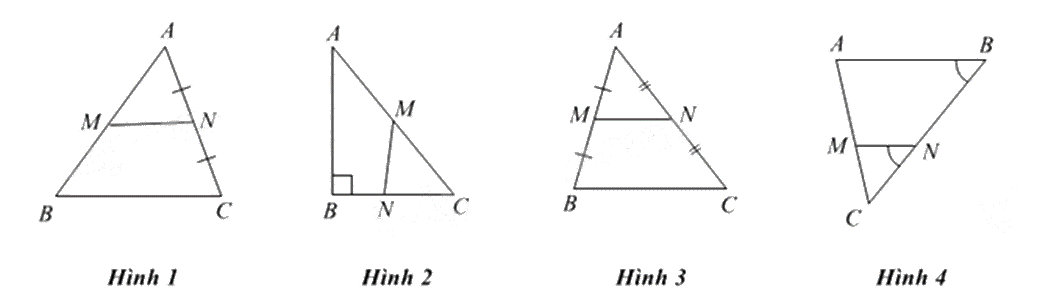
Đoạn thẳng MN là đường trung bình của tam giác ABC trong hình vẽ nào?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho tam giác ABC, AD là đường phân giác của \(\widehat {BAC}\left( {D \in BC} \right)\). Tỉ lệ thức nào sau đây đúng?
\(\frac{{AB}}{{BD}} = \frac{{AC}}{{BC}}\).
\(\frac{{AD}}{{AC}} = \frac{{BD}}{{DC}}\).
\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
\(\frac{{DB}}{{DC}} = \frac{{BC}}{{AC}}\).
Cho $\Delta ABC\backsim \Delta DEF$, biết \(\widehat A = 75^\circ ,\widehat B = 50^\circ \). Khi đó \(\widehat F\) bằng
\(65^\circ \).
\(85^\circ \).
\(55^\circ \).
\(75^\circ \).
Cho \(\Delta MNP\) và \(\Delta DEF\) có \(\widehat M = \widehat D\). Điều kiện để $\Delta MNP\backsim \Delta DEF$ theo trường hợp góc – góc là
\(\widehat N = \widehat F\).
\(\widehat P = \widehat F\).
\(\widehat M = \widehat E\).
\(\widehat P = \widehat E\).
Cho $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số đồng dạng $k=1$ thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng là
2.
$\frac{1}{2}$.
$1$.
$3$.
Một hộp có 30 quả bóng được đánh số từ 1 đến 30, đồng thời các quả bóng từ 1 đến 10 được sơn màu cam và các quả bóng còn lại được sơn màu xanh. Các quả bóng có kích cỡ và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp. Số kết quả thuận lợi của biến cố: “Quả bóng được lấy ra được sơn màu cam” là
10.
20.
15.
30.
Một hộp chứa 10 tấm thẻ cùng loại được đánh số thứ tự 4 đến 13. An lấy ra ngẫu nhiên một thẻ từ hộp. Xác suất để chọn ra thẻ ghi số chẵn là
0,2.
0,3.
0,4.
0,5.
Cho tam giác ABC cân tại A có M là trung điểm của BC. Kẻ Mx // AC cắt AB tại E, kẻ My //AB cắt AC tại F.
a) E, F là trung điểm của AB, AC.
b) \(EF = \frac{1}{2}AC\).
c) ME = MF.
d) AE = AF.
Bạn An gieo một con xúc xắc nhiều lần và thống kê kết quả các lần gieo vào bảng sau:

a) Bạn An đã gieo xúc xắc 50 lần.
b) Số kết quả thuận lợi của biến cố “Xuất hiện mặt 4 chấm” là 4.
c) Xác suất của biến cố “Xuất hiện mặt có số chấm chẵn” là 0,6.
d) Xác suất của biến cố xuất hiện mặt có số chấm không nhỏ hơn 3” là \(\frac{{14}}{{25}}\).
Cho đường thẳng \(\left( d \right):y = - 2x + 3\). Tìm \(m\) để đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( { - m; - 3} \right)\).
Đáp án:
Tính giá trị của \(x\), biết: \(x{\left( {x + 3} \right)^2} - 3x = {\left( {x + 2} \right)^3} + 1\).
(Kết quả ghi dưới dạng số thập phân)
Đáp án:
Một chiếc thuyền xuất phát từ vị trí \(I\) chở hàng cho hai hòn đảo \(A\) và \(B\) theo phương thẳng (được minh họa như trong hình vẽ). Một người đứng ở vị trí \(K\) trên bờ quan sát ba điểm thẳng hàng \(I,{\mkern 1mu} A,{\mkern 1mu} B\). Người đó nhận thấy \(\widehat {IKA} = \widehat {AKB}\). Biết rằng thuyền đi từ vị trí \(I\) đến hòn đảo \(A\) là \(500{\mkern 1mu} m\); từ hòn đảo \(A\) đến hòn đảo \(B\) là \(6{\mkern 1mu} km\) và khoảng cách từ người đó đến vị trí \(I\) là \(1{\mkern 1mu} km\). Tính khoảng cách từ người đó (vị trí \(K\)) đến hòn đảo \(B\) theo km?
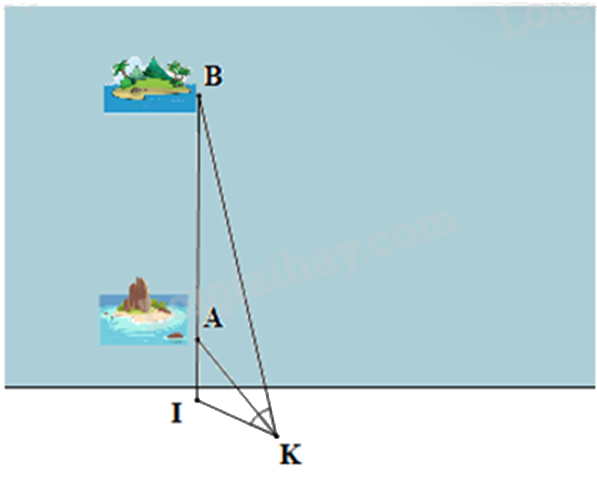
Đáp án:
Bạn An vào cửa hàng Lotteria và dự định mua một suất gà rán. Khi đọc menu, bạn An thấy cửa hàng đang có các món như sau: combo gà rán (ưu đãi) có giá 97 000 đồng, combo gà viên (ưu đãi) có giá 84 000 đồng, gà rán – 1 miếng có giá 35 000 đồng, gà rán – 2 miếng có giá 68 000 đồng, gà rán – 3 miếng có giá 101 000 đồng, cánh gà chiên – 3 miếng có giá 48 000 nghìn đồng. Bạn An cảm thấy món nào cũng ngon và dự định sẽ nhắm mắt chỉ tay chọn ngẫu nhiên một món. Tính xác suất “Món gà được bạn An chọn có giá dưới 70 000 đồng”. (Kết quả ghi dưới dạng số thập phân)
Đáp án:
Có hai loại dung dịch muối I và II. Người ta hoà 200 gam dung dịch muối I với 300 gam dung dịch muối II thì được một dung dịch có nồng độ muối là 33%. Tính nồng độ muối trong dung dịch I và II, biết rằng nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20%.
Cho tam giác ABC (AB < AC) vuông tại A có đường cao AH.
a) Chứng minh rằng $\Delta ABC\backsim \Delta HAC$.
b) Lấy điểm I thuộc đoạn AH (I không trùng với A, H). Qua B kẻ đường thẳng vuông góc với CI tại K. Chứng minh rằng \(CH.CB = CI.CK\).
c) Tia BK cắt tia HA tại điểm D. Chứng minh \(CH.CB + DK.DB = C{D^2}\).
Giải phương trình \(2x{\left( {8x - 1} \right)^2}\left( {4x - 1} \right) = 9\).
Đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là một đường thẳng luôn đi qua
gốc toạ độ \(O\left( {0;0} \right)\).
điểm \(A\left( {1;0} \right)\).
điểm \(B\left( {0;1} \right)\).
điểm \(C\left( {1;1} \right)\).
Đáp án : A
Dựa vào kiến thức về đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\).
Đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là một đường thẳng luôn đi qua gốc toạ độ \(O\left( {0;0} \right)\).
Đáp án A
Hệ số góc của đường thẳng \(y = x - 2\) là:
-2.
2.
-1.
1.
Đáp án : D
Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là a.
Hệ số góc của đường thẳng \(y = x - 2\) là \(a = 1\).
Đáp án D
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
\(0x + 5 = 0\).
\(2{x^2} - 3 = 0\).
\(\frac{3}{x} - 2 = 0\).
\(2x + 1 = 0\).
Đáp án : D
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\left( {a \ne 0} \right)\).
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\left( {a \ne 0} \right)\).
Do đó \(2x + 1 = 0\) là phương trình bậc nhất một ẩn.
Đáp án D
Phương trình \(3 - 2x = 0\) có nghiệm là:
\(x = 3\).
\(x = \frac{2}{3}\).
\(x = \frac{3}{2}\).
\(x = \frac{{ - 3}}{2}\).
Đáp án : C
Giải phương trình bậc nhất một ẩn:
\(\begin{array}{l}ax + b = 0\\ax = - b\\x = - \frac{b}{a}\end{array}\)
Ta có:
\(\begin{array}{l}3 - 2x = 0\\ - 2x = - 3\\x = \frac{3}{2}\end{array}\)
Vậy \(x = \frac{3}{2}\)
Đáp án C
Cho hình vẽ sau:
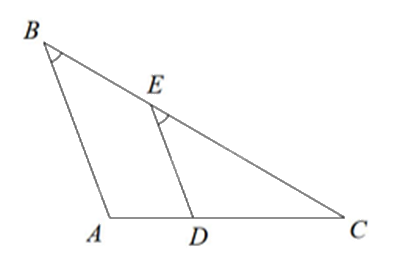
Hệ thức theo Định lí Thalès của hình trên là:
\(\frac{{CE}}{{CB}} = \frac{{CD}}{{CA}}\).
\(\frac{{BE}}{{CB}} = \frac{{CA}}{{AD}}\).
\(\frac{{CE}}{{BE}} = \frac{{AD}}{{CD}}\).
\(\frac{{DE}}{{AB}} = \frac{{AC}}{{AD}}\).
Đáp án : A
Chứng minh DE // AB.
Sử dụng định lí Thalès để xác định.
Vì \(\widehat {ABC} = \widehat {DEC}\) mà hai góc này ở vị trí đồng vị nên \(DE//BC\).
Áp dụng định lí Thalès ta có: \(\frac{{CE}}{{CB}} = \frac{{CD}}{{CA}}\) nên A đúng.
Đáp án A
Cho các hình sau:
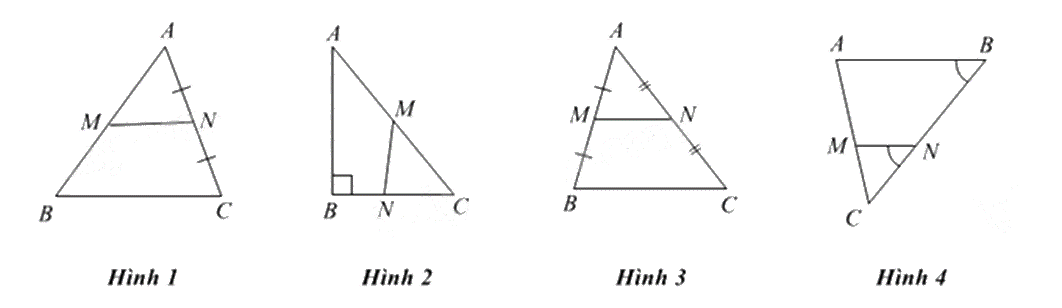
Đoạn thẳng MN là đường trung bình của tam giác ABC trong hình vẽ nào?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đáp án : C
Đường trung bình của tam giác là đoạn thẳng đi qua trung điểm của hai cạnh của tam giác đó.
Trong Hình 3, xét tam giác ABC ta có: M là trung điểm của AB, N là trung điểm của AC nên MN là đường trung bình của tam giác ABC.
Đáp án C
Cho tam giác ABC, AD là đường phân giác của \(\widehat {BAC}\left( {D \in BC} \right)\). Tỉ lệ thức nào sau đây đúng?
\(\frac{{AB}}{{BD}} = \frac{{AC}}{{BC}}\).
\(\frac{{AD}}{{AC}} = \frac{{BD}}{{DC}}\).
\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
\(\frac{{DB}}{{DC}} = \frac{{BC}}{{AC}}\).
Đáp án : C
Sử dụng tính chất của đường phân giác trong tam giác.
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
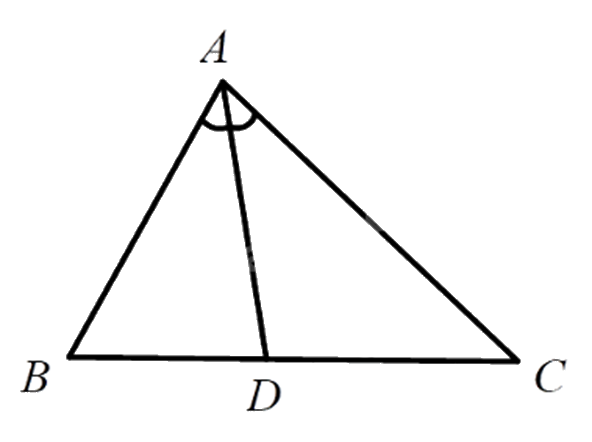
Xét tam giác ABC có AD là đường phân giác của \(\widehat {BAC}\) nên \(\frac{{AB}}{{BD}} = \frac{{AC}}{{DC}}\) hay \(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
Đáp án C
Cho $\Delta ABC\backsim \Delta DEF$, biết \(\widehat A = 75^\circ ,\widehat B = 50^\circ \). Khi đó \(\widehat F\) bằng
\(65^\circ \).
\(85^\circ \).
\(55^\circ \).
\(75^\circ \).
Đáp án : C
Từ hai tam giác đồng dạng suy ra góc tương ứng bằng \(\widehat F\).
Áp dụng định lí tổng ba góc trong một tam giác bằng \(180^\circ \) suy ra số đo \(\widehat F\).
Vì $\Delta ABC\backsim \Delta DEF$ nên \(\widehat F = \widehat C\) (hai góc tương ứng)
Xét tam giác ABC ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) nên \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 75^\circ - 50^\circ = 55^\circ \).
Do đó \(\widehat F = 55^\circ \).
Đáp án C
Cho \(\Delta MNP\) và \(\Delta DEF\) có \(\widehat M = \widehat D\). Điều kiện để $\Delta MNP\backsim \Delta DEF$ theo trường hợp góc – góc là
\(\widehat N = \widehat F\).
\(\widehat P = \widehat F\).
\(\widehat M = \widehat E\).
\(\widehat P = \widehat E\).
Đáp án : B
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu chúng có hai cặp góc bằng nhau.
Để $\Delta MNP\backsim \Delta DEF\left( g.g \right)$ có \(\widehat M = \widehat D\) thì ta cần thêm \(\widehat P = \widehat F\) hoặc \(\widehat N = \widehat E\) nên ta chọn B.
Đáp án B
Cho $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số đồng dạng $k=1$ thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng là
2.
$\frac{1}{2}$.
$1$.
$3$.
Đáp án : C
Nếu $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số đồng dạng $k$ thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng $\frac{1}{k}$.
Để $\Delta MNP\backsim \Delta A'B'C'$ theo tỉ số đồng dạng $k=1$ thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng $k'=\frac{1}{k}=\frac{1}{1}=1$.
Đáp án C
Một hộp có 30 quả bóng được đánh số từ 1 đến 30, đồng thời các quả bóng từ 1 đến 10 được sơn màu cam và các quả bóng còn lại được sơn màu xanh. Các quả bóng có kích cỡ và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp. Số kết quả thuận lợi của biến cố: “Quả bóng được lấy ra được sơn màu cam” là
10.
20.
15.
30.
Đáp án : A
Xác định các số thoả mãn quả bóng được sơn màu cam.
Số kết quả thuận lợi của biến cố “Quả bóng được lấy ra có màu cam” là 10, đó là các quả bóng từ 1 đến 10.
Đáp án A
Một hộp chứa 10 tấm thẻ cùng loại được đánh số thứ tự 4 đến 13. An lấy ra ngẫu nhiên một thẻ từ hộp. Xác suất để chọn ra thẻ ghi số chẵn là
0,2.
0,3.
0,4.
0,5.
Đáp án : D
Xác định các thẻ ghi số chẵn, ta được số các kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể (tổng số thẻ).
Các kết quả thuận lợi cho biến cố “lấy được thẻ ghi số chẵn” là: 4; 6; 8; 10; 12.
Do đó có 5 kết quả thuận lợi.
Có 10 kết quả có thể khi lấy ngẫu nhiên một thẻ từ hộp.
Xác suất để chọn được thẻ ghi số chẵn là: \(\frac{5}{{10}} = 0,5\).
Đáp án D
Cho tam giác ABC cân tại A có M là trung điểm của BC. Kẻ Mx // AC cắt AB tại E, kẻ My //AB cắt AC tại F.
a) E, F là trung điểm của AB, AC.
b) \(EF = \frac{1}{2}AC\).
c) ME = MF.
d) AE = AF.
a) E, F là trung điểm của AB, AC.
b) \(EF = \frac{1}{2}AC\).
c) ME = MF.
d) AE = AF.
a) Chứng minh ME là đường trung bình của tam giác ABC nên E là trung điểm của AB.
Chứng minh MF là đường trung bình của tam giác АВС nên F là trung điểm của AC.
b) Sử dụng tính chất của đường trung bình.
c) Sử dụng tính chất của đường trung bình và tính chất của tam giác cân.
d) Sử dụng tính chất của trung điểm.
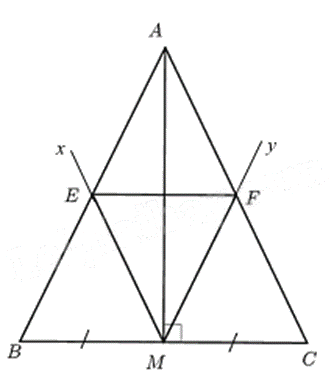
a) Đúng
Ta có M là trung điểm của BC và ME // AC nên ME là đường trung bình của tam giác ABC.
Do đó E là trung điểm của AB.
Ta có M là trung điểm của BC và MF // AB nên MF là đường trung bình của tam giác АВС.
Do đó F là trung điểm của AC.
Vậy E, F là trung điểm của AB, AC.
b) Sai
Vì E, F là trung điểm của cạnh AB, AC (câu a) nên EF là đường trung bình của tam giác ABC.
Do đó \(EF = \frac{1}{2}BC\).
Mà AC và BC không bằng nhau nên b sai.
c) Đúng
Ta có: ME, MF là các đường trung bình của tam giác ABC.
Do đó \(ME = \frac{1}{2}AC,MF = \frac{1}{2}AB\).
Mà tam giác ABC cân nên AB = AC.
Suy ra ME = MF.
d) Đúng
Ta có E, F là trung điểm của cạnh AB, AC.
Do đó \(AE = \frac{1}{2}AB,AF = \frac{1}{2}AC\).
Suy ra AE = AF.
Đáp án: ĐSĐĐ
Bạn An gieo một con xúc xắc nhiều lần và thống kê kết quả các lần gieo vào bảng sau:

a) Bạn An đã gieo xúc xắc 50 lần.
b) Số kết quả thuận lợi của biến cố “Xuất hiện mặt 4 chấm” là 4.
c) Xác suất của biến cố “Xuất hiện mặt có số chấm chẵn” là 0,6.
d) Xác suất của biến cố xuất hiện mặt có số chấm không nhỏ hơn 3” là \(\frac{{14}}{{25}}\).
a) Bạn An đã gieo xúc xắc 50 lần.
b) Số kết quả thuận lợi của biến cố “Xuất hiện mặt 4 chấm” là 4.
c) Xác suất của biến cố “Xuất hiện mặt có số chấm chẵn” là 0,6.
d) Xác suất của biến cố xuất hiện mặt có số chấm không nhỏ hơn 3” là \(\frac{{14}}{{25}}\).
a) Dựa vào bảng thống kê số lần để tính tổng số lần gieo.
b) Quan sát bảng xác định số lần xuất hiện mặt 4 chấm.
c) Xác định số kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
d) Xác định số kết quả thuận lợi cho biến cố (số chấm không nhỏ hơn 3 ta tính các kết quả số chấm 3, 4, 5, 6).
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
a) Đúng
Bạn An đã gieo tổng số lần là:
10 + 8 + 6 + 12 + 4 + 10 = 50 (lần)
b) Sai
Quan sát bảng, ta thấy số kết quả thuận lợi cho biến cố “Xuất hiện mặt 4 chấm” là 12.
c) Đúng
Kết quả thuận lợi cho biến cố “Xuất hiện mặt có số chấm chẵn” là:
12 + 8 + 10 = 30.
Xác suất của biến cố “Xuất hiện số mặt có 30 số chấm chẵn” là: \(\frac{{30}}{{50}} = 0,6\).
d) Sai
Kết quả thuận lợi của biến cố “Xuất hiện mặt có số chấm không nhỏ hơn 3" là:
6 + 12 + 4 + 10 = 32
Do đó xác suất của biến cố đó là: \(\frac{{36}}{{50}} = \frac{{16}}{{25}}\).
Đáp án: ĐSĐS
Cho đường thẳng \(\left( d \right):y = - 2x + 3\). Tìm \(m\) để đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( { - m; - 3} \right)\).
Đáp án:
Đáp án:
Thay toạ độ điểm \(A\left( { - m; - 3} \right)\) vào \(\left( d \right):y = - 2x + 3\) để tìm m
Thay toạ độ điểm \(A\left( { - m; - 3} \right)\) vào \(\left( d \right):y = - 2x + 3\), ta được:
\(\begin{array}{l} - 2\left( { - m} \right) + 3 = - 3\\2m = - 3 - 3\\2m = - 6\\m = \left( { - 6} \right):2\\m = - 3\end{array}\)
Đáp án: -3
Tính giá trị của \(x\), biết: \(x{\left( {x + 3} \right)^2} - 3x = {\left( {x + 2} \right)^3} + 1\).
(Kết quả ghi dưới dạng số thập phân)
Đáp án:
Đáp án:
Đưa phương trình về phương trình bậc nhất một ẩn để tìm x.
Ta có: \(x{\left( {x + 3} \right)^2} - 3x = {\left( {x + 2} \right)^3} + 1\)
\(\begin{array}{l}x\left( {{x^2} + 6x + 9} \right) - 3x = {x^3} + 6{x^2} + 12x + 8 + 1\\{x^3} + 6{x^2} + 9x - 3x - {x^3} - 6{x^2} - 12x - 9 = 0\\\left( {{x^3} - {x^3}} \right) + \left( {6{x^2} - 6{x^2}} \right) + \left( {9x - 3x - 12x} \right) - 9 = 0\\ - 6x = 9\\x = \frac{{ - 3}}{2} = - 1,5\end{array}\)
Vậy \(x = - 1,5\)
Đáp án: -1,5
Một chiếc thuyền xuất phát từ vị trí \(I\) chở hàng cho hai hòn đảo \(A\) và \(B\) theo phương thẳng (được minh họa như trong hình vẽ). Một người đứng ở vị trí \(K\) trên bờ quan sát ba điểm thẳng hàng \(I,{\mkern 1mu} A,{\mkern 1mu} B\). Người đó nhận thấy \(\widehat {IKA} = \widehat {AKB}\). Biết rằng thuyền đi từ vị trí \(I\) đến hòn đảo \(A\) là \(500{\mkern 1mu} m\); từ hòn đảo \(A\) đến hòn đảo \(B\) là \(6{\mkern 1mu} km\) và khoảng cách từ người đó đến vị trí \(I\) là \(1{\mkern 1mu} km\). Tính khoảng cách từ người đó (vị trí \(K\)) đến hòn đảo \(B\) theo km?
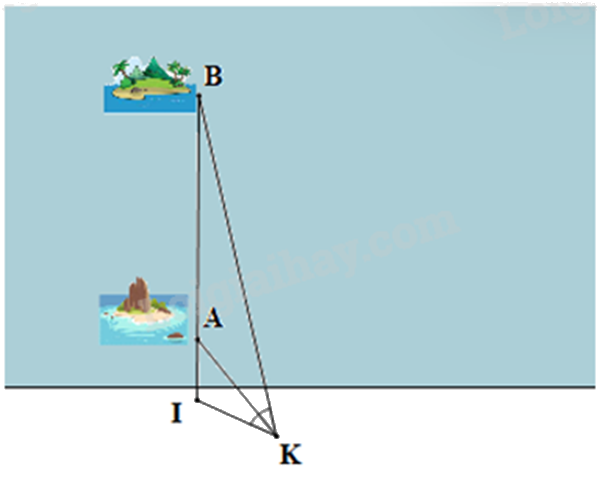
Đáp án:
Đáp án:
Đưa về cùng đơn vị.
Chứng minh AK là đường phân giác của \(\widehat {IKB}\).
Áp dụng tính chất đường phân giác trong \(\Delta IKB\) có \(\frac{{AB}}{{AI}} = \frac{{BK}}{{IK}}\).
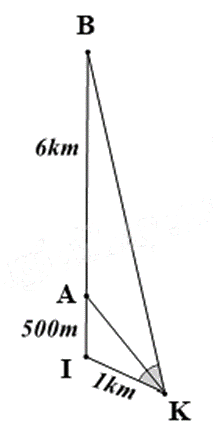
Theo bài ra ta có: \(IA = 500{\mkern 1mu} m = 0,5{\mkern 1mu} km\), \(AB = 6{\mkern 1mu} km\), \(IK = 1{\mkern 1mu} km\).
Vì \(\widehat {IKA} = \widehat {AKB}\) nên AK là tia phân giác của \(\widehat {IKB}\), suy ra AK là đường phân giác của tam giác IKB.
Áp dụng tính chất đường phân giác trong \(\Delta IKB\), ta có:
\(\frac{{AB}}{{AI}} = \frac{{BK}}{{IK}}\) hay \(\frac{6}{{0,5}} = \frac{{BK}}{1}\)
Suy ra \(BK = \frac{6}{{0,5}} = 12\left( {km} \right)\)
Vậy khoảng cách từ người đó (vị trí \(K\)) đến hòn đảo \(B\) là \(BK = 12{\mkern 1mu} km\).
Đáp án: 12
Bạn An vào cửa hàng Lotteria và dự định mua một suất gà rán. Khi đọc menu, bạn An thấy cửa hàng đang có các món như sau: combo gà rán (ưu đãi) có giá 97 000 đồng, combo gà viên (ưu đãi) có giá 84 000 đồng, gà rán – 1 miếng có giá 35 000 đồng, gà rán – 2 miếng có giá 68 000 đồng, gà rán – 3 miếng có giá 101 000 đồng, cánh gà chiên – 3 miếng có giá 48 000 nghìn đồng. Bạn An cảm thấy món nào cũng ngon và dự định sẽ nhắm mắt chỉ tay chọn ngẫu nhiên một món. Tính xác suất “Món gà được bạn An chọn có giá dưới 70 000 đồng”. (Kết quả ghi dưới dạng số thập phân)
Đáp án:
Đáp án:
Xác định tập hợp các kết quả có thể xảy ra đối với món gà mà bạn An chọn, từ đó suy ra số kết quả có thể xảy ra.
Xác định các kết quả thuận lợi cho biến cố “Món gà được bạn An chọn có giá dưới 70 000 đồng”, suy ra số kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
Tập hợp các kết quả có thể xảy ra đối với món gà mà bạn An chọn là:
A = {combo gà rán; combo gà viên; gà rán - 1 miếng; gà rán – 2 miếng; gà rán – 3 miếng; cánh gà chiên – 3 miếng}.
Vậy có 6 kết quả có thể xảy ra.
Kết quả thuận lợi cho biến cố “Món gà được bạn An chọn có giá dưới 70 000 đồng” là: gà rán – miếng giá 35 000 đồng; gà rán – 2 miếng giá 68 000 và cánh gà chiên – 3 miếng giá 48 000 đồng.
Do đó, có 3 kết quả thuận lợi cho biến cố.
Vậy xác suất của biến cố “Món gà được bạn An chọn có giá dưới 70 000 đồng” là: \(\frac{3}{6} = \frac{1}{2} = 0,5\).
Đáp án: 0,5
Có hai loại dung dịch muối I và II. Người ta hoà 200 gam dung dịch muối I với 300 gam dung dịch muối II thì được một dung dịch có nồng độ muối là 33%. Tính nồng độ muối trong dung dịch I và II, biết rằng nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20%.
Gọi nồng độ muối trong dung dịch I là \(x\left( \% \right)\) với \(x > 20\).
Biểu diễn lượng muối có trong dung dịch I, nồng độ muối trong dung dịch II, lượng muối trong dung dịch II, khối lượng muối trong dung dịch sau khi trộn hai dung dịch theo \(x\).
Tính khối lượng dung dịch muối sau khi trộn hai dung dịch, từ đó lập phương trình biểu diễn nồng độ muối sai khi trộn hai dung dịch I và II.
Giải phương trình và kiểm tra điều kiện.
Từ đó tính nồng độ muối trong dung dịch II.
Gọi nồng độ muối trong dung dịch I là \(x\left( \% \right)\) với \(x > 20\).
Khi đó lượng muối có trong dung dịch I là:
\(200.\frac{x}{{100}} = 2x\left( g \right)\).
Do nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20% nên nồng độ muối trong dung dịch II là: \(x - 20\left( \% \right)\)
Khi đó lượng muối trong dung dịch II là: \(300.\frac{{x - 20}}{{100}} = 3\left( {x - 20} \right)\left( g \right)\)
Khối lượng muối trong dung dịch sau khi trộn hai dung dịch là: \(2x + 3\left( {x - 20} \right)\left( g \right)\)
Khối lượng dung dịch muối sau khi trộn hai dung dịch là: \(200 + 300 = 500\left( g \right)\)
Do sau khi trộn hai dung dịch I và II thì được một dung dịch có nồng độ muối là 33% nên ta có phương trình:
\(\frac{{2x + 3\left( {x - 20} \right)}}{{500}}.100\% = 33\% \)
Giải phương trình, ta được:
\(\frac{{2x + 3\left( {x - 20} \right)}}{{500}}.100\% = 33\% \).
\(\frac{{2x + 3\left( {x - 20} \right)}}{5} = 33\)
\(\begin{array}{l}2x + 3x - 60 = 33.5\\5x - 60 = 165\\5x = 165 + 60\\5x = 225\\x = 225:5\\x = 45\left( {TM} \right)\end{array}\)
Suy ra nồng độ muối trong dung dịch II là: 45 – 20 = 25(%).
Vậy nồng độ muối của dung dịch I và II lần lượt là 45% và 25%.
Cho tam giác ABC (AB < AC) vuông tại A có đường cao AH.
a) Chứng minh rằng $\Delta ABC\backsim \Delta HAC$.
b) Lấy điểm I thuộc đoạn AH (I không trùng với A, H). Qua B kẻ đường thẳng vuông góc với CI tại K. Chứng minh rằng \(CH.CB = CI.CK\).
c) Tia BK cắt tia HA tại điểm D. Chứng minh \(CH.CB + DK.DB = C{D^2}\).
a) Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat {BAC} = \widehat {AHC} = 90^\circ \) (gt)
\(\widehat {ACB}\) chung
nên $\Delta ABC\backsim \Delta HAC$ (g.g)
b) Chứng minh $\Delta CHI\backsim \Delta CKB$ (g.g) suy ra $CH\cdot CB=CI\cdot CK$
c) Chứng minh \(I\) là trực tâm của \(\Delta BDC\), suy ra \(BI \bot DC\).
Gọi \(M\) là giao điểm của BI và DC, khi đó \(BM \bot CD\) nên \(\widehat {BMC} = 90^\circ \)
Chứng minh $\Delta CMI\backsim \Delta CDK$ (g.g) suy ra \(CD \cdot CM = CI \cdot CK\)
Kết hợp với phần b) ta được \(CH \cdot CB = CD \cdot CM\left( { = CI \cdot CK} \right)\) (1)
Chứng minh $\Delta MDB \backsim \Delta KDC$ (g.g) suy ra \(DK \cdot DB = DM \cdot DC\) (2)
Cộng (1) và (2) để được điều phải chứng minh.
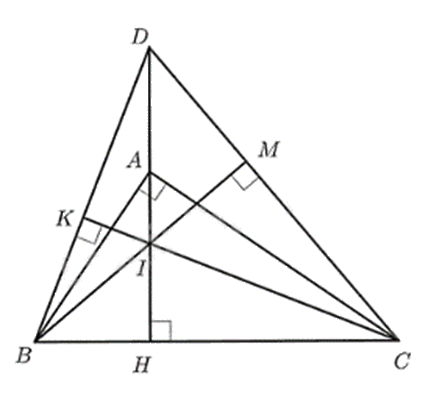
a) Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat {BAC} = \widehat {AHC} = 90^\circ \) (gt)
\(\widehat {ACB}\) chung
nên $\Delta ABC\backsim \Delta HAC$ (g.g)
b) Xét \(\Delta CHI\) và \(\Delta CKB\) có:
\(\widehat {CHI} = \widehat {CKB} = 90^\circ \) (gt)
\(\,\widehat {HCI}\) chung
nên $\Delta CHI\backsim \Delta CKB$ (g.g)
suy ra \(\frac{{CH}}{{CK}} = \frac{{CI}}{{CB}}\)
do đó \(CH \cdot CB = CI \cdot CK\)
c) Vì \(DH \bot BC\) (do \(HA \bot BC\), D thuộc tia HA) nên DH là đường cao của \(\Delta BDC\).
Vì \(CK \bot BD\) (do \(CI \bot BK\)) nên CK là đường cao của \(\Delta BDC\).
Mà DH cắt CK tại I nên \(I\) là trực tâm của \(\Delta BDC\), suy ra \(BI \bot DC\).
Gọi \(M\) là giao điểm của BI và DC, khi đó \(BM \bot CD\) nên \(\widehat {BMC} = 90^\circ \)
Xét \(\Delta CMI\) và \(\Delta CDK\), ta có:
\(\widehat {CMI} = \widehat {CKD} = 90^\circ \) (cmt)
\(\widehat {DCK}\) chung
nên $\Delta CMI\backsim \Delta CKD$ (g.g)
suy ra \(\frac{{CM}}{{CK}} = \frac{{CI}}{{CD}}\), do đó \(CD \cdot CM = CI \cdot CK\)
Mà từ phần b) ta có: \(CH \cdot CB = CI \cdot CK\)
Suy ra \(CH \cdot CB = CD \cdot CM\left( { = CI \cdot CK} \right)\) (1)
Xét \(\Delta MDB\) và \(\Delta KDC\), ta có:
\(\widehat {DMB} = \widehat {DKC} = 90^\circ \) (cmt)
\(\widehat {BDC}\) chung
nên $\Delta MDB \backsim \Delta KDC$ (g.g)
suy ra \(\frac{{DB}}{{DC}} = \frac{{DM}}{{DK}}\), do đó \(DK \cdot DB = DM \cdot DC\) (2)
Từ (1) và (2) ta có:
\(CH \cdot CB + DK \cdot DB = CD \cdot CM + DM \cdot DC\)\( = DC \cdot (MD + MC) = D{C^2}\)
Giải phương trình \(2x{\left( {8x - 1} \right)^2}\left( {4x - 1} \right) = 9\).
Biến đổi phương trình để xuất hiện dạng \(A\left( {A - 1} \right)\left( {A + 1} \right) = 72\).
Đặt \(y = A - 1\), đưa phương trình về dạng \(A\left( y \right).B\left( y \right) = 0\).
Giải phương trình để tìm y, từ đó suy ra giá trị x tương ứng.
Ta có:
\(\begin{array}{l}2x{\left( {8x - 1} \right)^2}\left( {4x - 1} \right) = 9\\x{\left( {8x - 1} \right)^2}\left( {8x - 2} \right) = 9\\8x{\left( {8x - 1} \right)^2}\left( {8x - 2} \right) = 72\end{array}\)
Đặt \(y = 8x - 1\), phương trình trở thành: \(\left( {y + 1} \right){y^2}\left( {y - 1} \right) = 72\)
Suy ra \(\left( {y + 1} \right){y^2}\left( {y - 1} \right) = 72\)
\(\begin{array}{l}\left( {y + 1} \right){y^2}\left( {y - 1} \right) - 72 = 0\\\left( {{y^2} - 1} \right).{y^2} - 72 = 0\\{y^4} - {y^2} - 72 = 0\\{y^4} - 9{y^2} + 8{y^2} - 72 = 0\\{y^2}\left( {{y^2} - 9} \right) + 8\left( {{y^2} - 9} \right) = 0\\\left( {{y^2} + 8} \right)\left( {{y^2} - 9} \right) = 0\end{array}\)
Mà \({y^2} + 8 > 0\) nên \({y^2} - 9 = 0\), suy ra \(y = 3\) hoặc \(y = - 3\).
+) Với \(y = 3\) thì \(8x - 1 = 3\) nên \(8x = 4\), suy ra \(x = \frac{4}{8} = \frac{1}{2}\).
+) Với \(y = - 3\) thì \(8x - 1 = - 3\) nên \(8x = - 2\), suy ra \(x = \frac{{ - 2}}{8} = \frac{{ - 1}}{4}\).
Vậy phương trình có nghiệm \(x = \frac{1}{2};x = \frac{{ - 1}}{4}\).
Kỳ thi học kì 2 Toán 8 đóng vai trò quan trọng trong việc đánh giá kết quả học tập của học sinh trong suốt một học kỳ. Việc làm quen với cấu trúc đề thi và luyện tập giải các đề thi thử là một phương pháp hiệu quả để chuẩn bị tốt nhất cho kỳ thi này. Đề thi học kì 2 Toán 8 Chân trời sáng tạo - Đề số 6 mà giaitoan.edu.vn cung cấp là một tài liệu tham khảo hữu ích, giúp học sinh tự tin hơn khi bước vào phòng thi.
Đề thi này bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính đã được học trong chương trình Toán 8 Chân trời sáng tạo. Cụ thể:
Giaitoan.edu.vn không chỉ cung cấp đề thi mà còn cung cấp cả đáp án chi tiết và lời giải cho từng bài tập. Điều này giúp học sinh tự kiểm tra kết quả và hiểu rõ hơn về phương pháp giải các bài toán. Dưới đây là một số hướng dẫn giải chi tiết cho một số bài tập tiêu biểu:
Lời giải:
Lời giải:
Diện tích hình thang được tính theo công thức: S = (a + b) * h / 2, trong đó a và b là độ dài hai đáy, h là chiều cao.
Thay số vào công thức: S = (5 + 7) * 4 / 2 = 24 cm2
Việc luyện tập với đề thi này mang lại nhiều lợi ích cho học sinh:
Để đạt kết quả tốt nhất trong kỳ thi học kì 2 Toán 8, học sinh nên:
Đề thi học kì 2 Toán 8 Chân trời sáng tạo - Đề số 6 là một tài liệu ôn tập hữu ích, giúp học sinh chuẩn bị tốt nhất cho kỳ thi quan trọng. Hãy luyện tập thường xuyên và áp dụng những lời khuyên trên để đạt kết quả cao nhất!