Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 1 Toán 8 - Đề số 4, một công cụ hữu ích giúp các em học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 8, bao gồm các dạng bài tập thường gặp và có đáp án chi tiết đi kèm.
Với đề thi này, các em có thể tự tin làm bài và kiểm tra kiến thức đã học, đồng thời phát hiện những lỗ hổng để khắc phục kịp thời.
Câu 1: Trong các biểu thức sau, biểu thức nào không phải đơn thức?
Phần trắc nghiệm (3 điểm)
Câu 1: Trong các biểu thức sau, biểu thức nào không phải đơn thức?
A. \({x^2}y\).
B. \( - 3x{y^2}z\).
C. \({x^2}y + 14x{y^2}\).
D. \(x\).
Câu 2: Thu gọn đa thức \(M = {x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + 8{x^2}y + \frac{2}{3}{x^2}y{z^5}\) ta được
A. \(M = - 7{x^2}y - \frac{1}{3}y\).
B. \(M = 9{x^2}y - \frac{1}{3}y\).
C. \(M = 9{x^2}y + \frac{1}{3}x - \frac{4}{3}{x^2}y{z^5}\).
D. \(M = 9{x^2}y + \frac{1}{3}y\).
Câu 3: Kết quả của phép tính \(5{x^2}\left( {2{x^4} - 1} \right)\) là
A. \(7{x^4} - 1\).
B. \(10{x^4} - 1\).
C. \(10{x^8} - 5{x^2}\).
D. \(10{x^6} - 5{x^2}\).
Câu 4: Đa thức \({x^2} - 4{y^2}\) phân tích thành nhân tử là
A. \(\left( {x - 4y} \right)\left( {x + 4y} \right)\).
B. \(\left( {x - 2y} \right)\left( {x + 2y} \right)\).
C. \({\left( {x - 2y} \right)^2}\).
D. \({\left( {x - 4y} \right)^2}\).
Câu 5: Giá trị của biểu thức \(M = \left( {x - y} \right)\left( {{x^2} + {y^2} + xy} \right)\) tại \(x = 1;y = - 2\) là
A. -7.
B. 7.
C. -9.
D. 9.
Câu 6: Giá trị lớn nhất của biểu thức \(A = - {\left( {x - 3} \right)^2} + 2023\) là
A. 3.
B. 2023.
C. 2248.
D. 2006.
Câu 7: Tất cả các số tự nhiên n để đơn thức \(2{x^n}{y^3}\) chia hết cho đơn thức \(4{x^3}{y^n}\) là :
A. \(n = 3\).
B. \(n \ge 3\).
C. \(n > 3\).
D. \(n \le 3\).
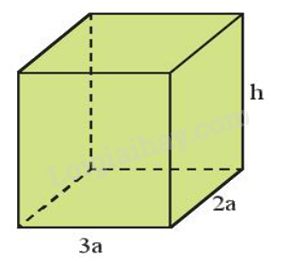
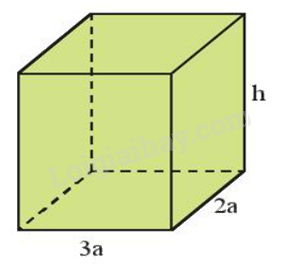
Câu 8: Cho hình hộp chữ nhật có các kích thước (tính theo cm) như hình sau:
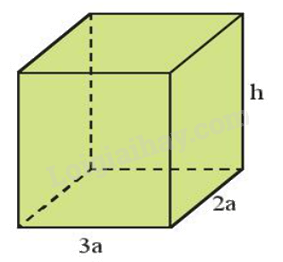
Đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật là:
A. \(10ah\).
B. \(6{a^2}h\).
C. \(6{a^2} + 10ah\).
D. \(12{a^2} + 10ah\).
Câu 9: Hình bình hành ABCD có số đo góc A bằng 2 lần số đo góc B. Khi đó số đo góc D là:
A. \({60^0}\).
B. \({120^0}\).
C. \({30^0}\).
D. \({45^0}\).
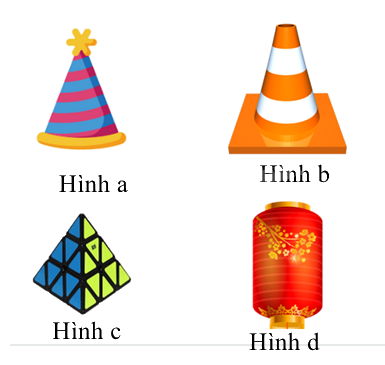
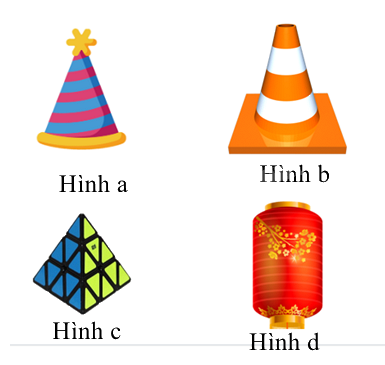
Câu 10: Hình nào sau đây trong thực tế có dạng hình chóp tam giác đều?
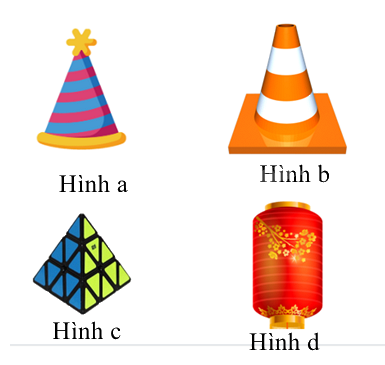
A. Hình a.
B. Hình b.
C. Hình c.
D. Hình d.
Câu 11: Cho hình chóp tam giác đều biết độ dài cạnh đáy là 18cm, trung đoạn của hình chóp là 20cm. Diện tích xung quanh của hình chóp tam giác đều đó là:
A. 540 cm2.
B. 1080 cm2.
C. 90 cm2.
D. 180 cm2
Câu 12: Bác Mai muốn may một cái lều cắm trại bằng vải bạt có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2,5m, chiều cao của cái lều trại là 3m. Tính thể tích khoảng không bên trong lều ?

A. \(18,75{m^3}\).
B. \(6,25{m^3}\).
C. \(15{m^3}\).
D. \(9,375{m^3}\).
Phần tự luận (7 điểm)
Bài 1. (1,5 điểm) Phân tích đa thức sau thành nhân tử:
a) \(8x{y^2} - 8xy + 2x\)
b) 25(x+5)2 – 9(x + 7)2
c) 3x2 + 4x – 4
Bài 2. (1,5 điểm)
1)Tìm x, biết:
a) \(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) = 1\)
b) \(3{x^2} + 7x = 10\)
2) Chứng tỏ biểu thức sau không phụ thuộc vào x
A = (x – 3)(x + 2) + (x – 4)(x + 4) – (2x – 1)x
Bài 3. (1 điểm) Một hình chữ nhật có chiều rộng là x (m) và chiều dài là y (m).
a) Viết biểu thức S và biểu thức P lần lượt biểu thị diện tích và chu vi của hình chữ nhật đó.
b) Nếu tăng chiều rộng của hình chữ nhật đó lên 3 lần và giữ nguyên chiều dài thì được một hình chữ nhật mới. Viết biểu thức Pm biểu thị chu vi của hình chữ nhật mới.
Bài 4. (2,5 điểm)
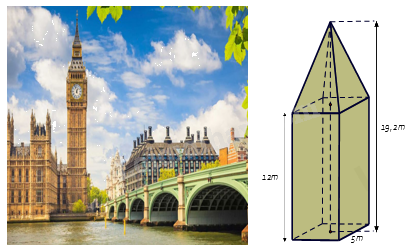
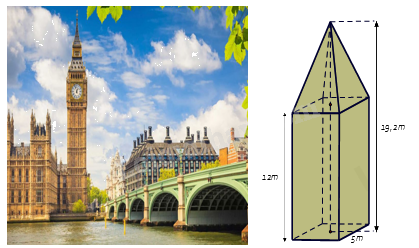
1.Tháp đồng hồ có phần dưới có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh dài 5m, chiều cao của hình hộp chữ nhật là 12m. Phần trên của tháp có dạng hình chóp tứ giác đều, các mặt bên là các tam giác cân chung đỉnh. Chiều cao của tháp đồng hồ là 19,2m.
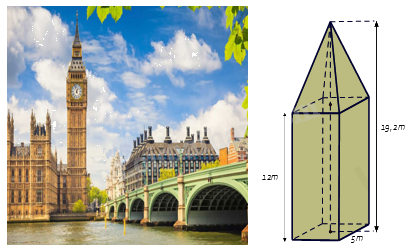
a) Tính theo mét chiều cao của phần trên của tháp đồng hồ.
b) Tính thể tích của tháp đồng hồ này.
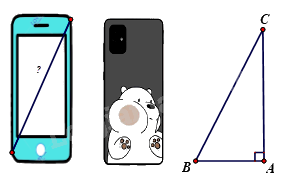
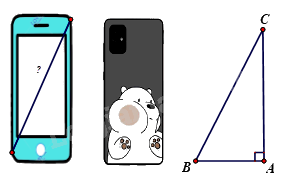
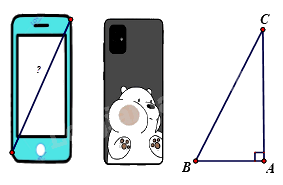
2. Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết 1\(inch \approx 2,54cm\), điện thoại có chiều rộng là 7cm; chiều dài là 15,5 cm. Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch ? (Làm tròn kết quả đến hàng đơn vị ).
Bài 5. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức: \(M = 5{x^2} + {y^2} + 2x\left( {y - 2} \right) + 8\)
- Hết -
Phần trắc nghiệm (3 điểm)
1. C | 2. B | 3. D | 4. B | 5. A | 6. B |
7. A | 8. D | 9. A | 10. C | 11. A | 12. B |
Câu 1: Trong các biểu thức sau, biểu thức nào không phải đơn thức?
A. \({x^2}y\). | B. \( - 3x{y^2}z\). |
C. \({x^2}y + 14x{y^2}\). | D. \(x\). |
Phương pháp
Dựa vào khái niệm đơn thức: Đơn thức là một biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.
Lời giải
Trong các biểu thức trên, chỉ có biểu thức \({x^2}y + 14x{y^2}\) không phải là đơn thức vì có chứa phép cộng.
Đáp án C.
Câu 2: Thu gọn đa thức \(M = {x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + 8{x^2}y + \frac{2}{3}{x^2}y{z^5}\) ta được
A. \(M = - 7{x^2}y - \frac{1}{3}y\). | B. \(M = 9{x^2}y - \frac{1}{3}y\). |
C. \(M = 9{x^2}y + \frac{1}{3}x - \frac{4}{3}{x^2}y{z^5}\). | D. \(M = 9{x^2}y + \frac{1}{3}y\). |
Phương pháp
Cộng, trừ các hạng tử đồng dạng để rút gọn.
Lời giải
\(\begin{array}{l}M = {x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + 8{x^2}y + \frac{2}{3}{x^2}y{z^5}\\ = {x^2}y + 8{x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + \frac{2}{3}{x^2}y{z^5}\\ = ({x^2}y + 8{x^2}y) - \frac{1}{3}y - \left( {\frac{2}{3}{x^2}y{z^5} - \frac{2}{3}{x^2}y{z^5}} \right)\\ = 9{x^2}y - \frac{1}{3}y - 0\\ = 9{x^2}y - \frac{1}{3}y\end{array}\)
Đáp án B.
Câu 3: Kết quả của phép tính \(5{x^2}\left( {2{x^4} - 1} \right)\) là
A. \(7{x^4} - 1\). | B. \(10{x^4} - 1\). |
C. \(10{x^8} - 5{x^2}\). | D. \(10{x^6} - 5{x^2}\). |
Phương pháp
Sử dụng quy tắc nhân đơn thức với đa thức.
Lời giải
\(\begin{array}{l}5{x^2}\left( {2{x^4} - 1} \right) = 5{x^2}.2{x^4} - 5{x^2}.1\\ = \left( {5.2} \right)\left( {{x^2}.{x^4}} \right) - 5{x^2}\\ = 10{x^6} - 5{x^2}\end{array}\)
Đáp án D.
Câu 4: Đa thức \({x^2} - 4{y^2}\) phân tích thành nhân tử là
A. \(\left( {x - 4y} \right)\left( {x + 4y} \right)\). | B. \(\left( {x - 2y} \right)\left( {x + 2y} \right)\). |
C. \({\left( {x - 2y} \right)^2}\). | D. \({\left( {x - 4y} \right)^2}\). |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
\({x^2} - 4{y^2} = \left( {x - 2y} \right)\left( {x + 2y} \right)\).
Đáp án B.
Câu 5: Giá trị của biểu thức \(M = \left( {x - y} \right)\left( {{x^2} + {y^2} + xy} \right)\) tại \(x = 1;y = - 2\) là
A. -7. | B. 7. |
C. -9. | D. 9. |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
\(M = \left( {x - y} \right)\left( {{x^2} + {y^2} + xy} \right) = {x^3} - {y^3}\).
Thay \(x = 1;y = - 2\) vào M, ta được \(M = {1^3} - {\left( { - 2} \right)^3} = 1 - \left( { - 8} \right) = 1 + 8 = 9\).
Đáp án A.
Câu 6: Giá trị lớn nhất của biểu thức \(A = - {\left( {x - 3} \right)^2} + 2023\) là
A. 3. | B. 2023. |
C. 2248. | D. 2006. |
Phương pháp
Dựa vào đặc điểm của bậc chẵn.
Lời giải
Ta có: \({(x - 3)^2} \ge 0 \Leftrightarrow - {(x - 3)^2} \le 0\) với mọi \(x \in \mathbb{R}\) nên \(A = - {\left( {x - 3} \right)^2} + 2023 \le 0 + 2023 = 2023\) với mọi \(x \in \mathbb{R}\).
Dấu bằng xảy ra chính là giá trị lớn nhất của biểu thức A.
Vậy giá trị lớn nhất của biểu thức A là 2023.
Đáp án B.
Câu 7: Tất cả các số tự nhiên n để đơn thức \(2{x^n}{y^3}\) chia hết cho đơn thức \(4{x^3}{y^n}\) là :
A. \(n = 3\). | B. \(n \ge 3\). |
C. \(n > 3\). | D. \(n \le 3\). |
Phương pháp
Để đa thức A chia hết cho đơn thức B thì mọi biến của đa thức A phải có bậc lớn hơn hoặc bằng bậc của các biến trong đơn thức B.
Lời giải
Để đa thức A chia hết cho đơn thức B thì biến x, y trong A phải có bậc lớn hơn hoặc bằng bậc của biến x, y trong B.
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}n \ge 3\\3 \ge n\end{array} \right.\\n = 3\end{array}\)
Suy ra n = 3.
Đáp án A.
Câu 8: Cho hình hộp chữ nhật có các kích thước (tính theo cm) như hình sau:
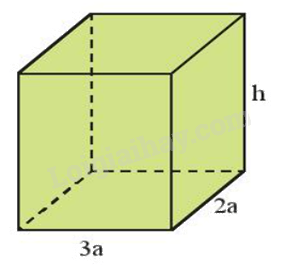
Đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật là:
A. \(10ah\). | B. \(6{a^2}h\). |
C. \(6{a^2} + 10ah\). | D. \(12{a^2} + 10ah\). |
Phương pháp
Dựa vào công thức tính diện tích hình vuông để viết đa thức.
Lời giải
Tổng diện tích các mặt chính là diện tích toàn phần của hình hộp chữ nhật.
Chu vi đáy: \((3a + 2a).2 = 5a.2 = 10a\)
Diện tích xung quanh: \(10a \cdot h = 10ah.\)
Tổng diện tích hai đáy: \(3a \cdot 2a \cdot 2 = 12{a^2}.\)
Suy ra tổng diện tích các mặt của hình hộp chữ nhật đó là \(S = 12{a^2} + 10ah.\)
Đa thức cần tìm là \(S = 12{a^2} + 10ah.\)
Đáp án D.
Câu 9: Hình bình hành ABCD có số đo góc A bằng 2 lần số đo góc B. Khi đó số đo góc D là:
A. \({60^0}\). | B. \({120^0}\). |
C. \({30^0}\). | D. \({45^0}\). |
Phương pháp
Dựa vào tính chất của hình bình hành và định lí tổng các góc của một tứ giác bằng 3600.
Lời giải
Vì ABCD là hình bình hành nên ta có: \(\widehat A = \widehat C;\widehat B = \widehat D\).
Vì \(\widehat A = 2\widehat B\) nên \(\widehat A + \widehat B + \widehat C + \widehat D = 2\widehat A + 2\widehat B = 2\widehat A + \widehat A = 3\widehat A = {360^0}\)
\( \Rightarrow \widehat A = {120^0} \Rightarrow \widehat B = \widehat D = \frac{{{{120}^0}}}{2} = {60^0}\)
Đáp án A.
Câu 10: Hình nào sau đây trong thực tế có dạng hình chóp tam giác đều?
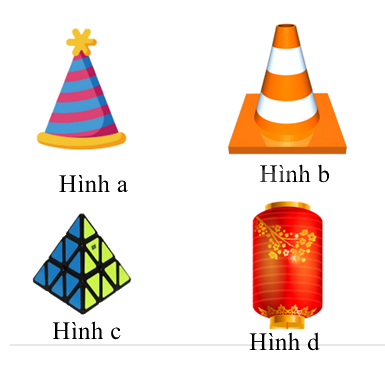
A. Hình a. | B. Hình b. |
C. Hình c. | D. Hình d. |
Phương pháp
Dựa vào đặc điểm của hình chóp tam giác.
Lời giải
Hình a không phải hình chóp tam giác vì đáy là hình tròn.
Hình b không phải hình chóp tam giác vì đáy là hình vuông.
Hình d không phải hình chóp.
Hình c là hình chóp tam giác vì có 1 đỉnh và đáy là hình tam giác đều.
Đáp án C.
Câu 11: Cho hình chóp tam giác đều biết độ dài cạnh đáy là 18cm, trung đoạn của hình chóp là 20cm. Diện tích xung quanh của hình chóp tam giác đều đó là:
A. 540 cm2. | B. 1080 cm2. |
C. 90 cm2. | D. 180 cm2. |
Phương pháp
Dựa vào công thức thính diện tích xung quanh hình chóp.
Lời giải
Diện tích xung quanh của hình chóp tam giác đều đó là:
\({S_{xq}} = \frac{{18.3}}{2}.20 = 540\left( {c{m^2}} \right)\)
Đáp án A.
Câu 12: Bác Mai muốn may một cái lều cắm trại bằng vải bạt có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2,5m, chiều cao của cái lều trại là 3m. Tính thể tích khoảng không bên trong lều ?

A. \(18,75{m^3}\). | B. \(6,25{m^3}\). |
C. \(15{m^3}\). | D. \(9,375{m^3}\). |
Phương pháp
Dựa vào công thức tính thể tích hình chóp tứ giác đều.
Lời giải
Thể tích khoảng không bên trong lều là :
\(V = \frac{1}{3}.(2,5.2,5).3 = 6,25\,\,\,({m^3})\)
Đáp án B.
Phần tự luận. (7 điểm)
Bài 1. (1,5 điểm) Phân tích đa thức sau thành nhân tử:
a) \(8x{y^2} - 8xy + 2x\)
b) 25(x+5)2 – 9(x + 7)2
c) 3x2 + 4x – 4
Phương pháp
Sử dụng các hằng đẳng thức đáng nhớ để phân tích đa thức.
Lời giải
a) \(8x{y^2} - 8xy + 2x\)
\(\begin{array}{l} = 2x\left( {4{y^2} - 4y + 1} \right)\\ = 2x{\left( {2y - 1} \right)^2}\end{array}\)
b) \(25{\left( {x + 5} \right)^2}-{\rm{ }}9{\left( {x{\rm{ }} + {\rm{ }}7} \right)^2}\)
\(\begin{array}{l} = {\left[ {5\left( {x + 5} \right)} \right]^2}-{\rm{ }}{\left[ {3\left( {x{\rm{ }} + {\rm{ }}7} \right)} \right]^2}\\ = \left[ {5\left( {x + 5} \right) - 3\left( {x + 7} \right)} \right]\left[ {5\left( {x + 5} \right) + 3\left( {x + 7} \right)} \right]\\ = \left( {5x + 25 - 3x - 21} \right)\left( {5x + 25 + 3x + 21} \right)\\ = \left( {2x + 4} \right)\left( {8x + 46} \right)\\ = 2\left( {x + 2} \right).2\left( {4x + 23} \right)\\ = 4\left( {x + 2} \right)\left( {4x + 23} \right)\end{array}\)
c) 3x2 + 4x – 4
\(\begin{array}{l}3{x^2} + 6x - 2x-4\\ = 3x\left( {x + 2} \right) - 2\left( {x + 2} \right)\\ = \left( {x + 2} \right)\left( {3x - 2} \right)\end{array}\)
Bài 2. (1,5 điểm)
1)Tìm x, biết:
a) \(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) = 1\)
b) \(3{x^2} + 7x = 10\)
2) Chứng tỏ biểu thức sau không phụ thuộc vào x
A = (x – 3)(x + 2) + (x – 4)(x + 4) – (2x – 1)x
Phương pháp
1) Sử dụng các phương pháp phân tích đa thức để tìm x.
2) Rút gọn biểu thức để chứng minh biểu thức không phụ thuộc vào x.
Lời giải
a) \(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) = 1\)
\(\begin{array}{l}{x^3} - {3^3} - {x^3} + 4x - 1 = 0\\4x - 28 = 0\\4x = 28\\x = 7\end{array}\)
Vậy x = 7.
b) \(3{x^2} + 7x = 10\)
\(\begin{array}{l}3{x^2} + 7x - 10 = 0\\\left( {3{x^2} - 3} \right) + \left( {7x - 7} \right) = 0\\3\left( {{x^2} - 1} \right) + 7\left( {x - 1} \right) = 0\\3\left( {x - 1} \right)\left( {x + 1} \right) + 7\left( {x - 1} \right) = 0\\\left( {x - 1} \right)\left( {3x + 3 + 7} \right) = 0\\\left( {x - 1} \right)\left( {3x + 10} \right) = 0\\\left[ \begin{array}{l}x - 1 = 0\\3x + 10 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 1\\x = - \frac{{10}}{3}\end{array} \right.\end{array}\)
Vậy x = 1 hoặc x = \( - \frac{{10}}{3}\).
2) A = (x – 3)(x + 2) + (x – 4)(x + 4) – (2x – 1)x
= x2 – 3x + 2x – 6 + x2 – 16 – 2x2 + x
= (x2 + x2 – 2x2) + (-3x + 2x + x) + (-6 – 16)
= 0 + 0 – 22
= - 22.
Vậy A không phụ thuộc vào x.
Bài 3. (1 điểm) Một hình chữ nhật có chiều rộng là x (m) và chiều dài là y (m).
a) Viết biểu thức S và biểu thức P lần lượt biểu thị diện tích và chu vi của hình chữ nhật đó.
b) Nếu tăng chiều rộng của hình chữ nhật đó lên 3 lần và giữ nguyên chiều dài thì được một hình chữ nhật mới. Viết biểu thức Pm biểu thị chu vi của hình chữ nhật mới.
Phương pháp
a) Sử dụng công thức tính diện tích và chu vi của hình chữ nhật để viết biểu thức.
b) Biểu diễn chiều rộng của hình chữ nhật mới theo chiều rộng của hình chữ nhật cũ và tính chu vi hình chữ nhật mới.
Lời giải
a) Công thức biểu thị diện tích hình chữ nhật là: S = x.y (m2).
Công thức biểu thị chu vi của hình chữ nhật là: P = 2(x + y) (m).
b) Chiều rộng của hình chữ nhật mới là: 3x (m).
Chu vi của hình chữ nhật mới là 2(3x + y) = 6x + 2y (m).
Vậy Pm = 6x + 2y.
Bài 4. (2,5 điểm)
1.Tháp đồng hồ có phần dưới có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh dài 5m, chiều cao của hình hộp chữ nhật là 12m. Phần trên của tháp có dạng hình chóp tứ giác đều, các mặt bên là các tam giác cân chung đỉnh. Chiều cao của tháp đồng hồ là 19,2m.
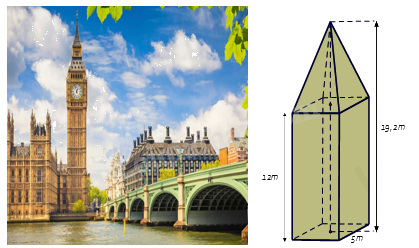
a) Tính theo mét chiều cao của phần trên của tháp đồng hồ.
b) Tính thể tích của tháp đồng hồ này.
2. Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết 1\(inch \approx 2,54cm\), điện thoại có chiều rộng là 7cm; chiều dài là 15,5 cm. Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch ? (Làm tròn kết quả đến hàng đơn vị ).
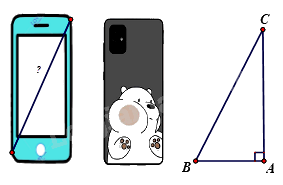
Phương pháp
1. a) Chiều cao phần trên của tháp đồng hồ bằng chiều cao của tháp đồng hồ - chiều cao hình hộp chữ nhật.
b) Tính thể tích phần hình chóp tứ giác đều + thể tích phần hình hộp chữ nhật ta được thể tích của tháp đồng hồ này.
2. Sử dụng định lí Pythagore.
Lời giải
1.
a) Chiều cao của phần trên của tháp đồng hồ là : 19,2 – 12 = 7,2 (m).
b) Thể tích của phần trên của tháp là : \({V_1} = \frac{1}{3}S.h = \frac{1}{3}{.5^2}.7,2 = 60{m^3}\)
Thể tích của phần dưới của tháp là : \({V_2} = S.h = 5.5.12 = 300{m^3}\).
Thể tích của tháp đồng hồ đó là : \(V = {V_1} + {V_2} = 60 + 300 = 360{m^3}\)
2. Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có :
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2}\\ \Rightarrow BC = \sqrt {A{C^2} + A{B^2}} = \sqrt {{{(15,5)}^2} + {{(7)}^2}} \approx 17(cm)\end{array}\)
Vì \(1\,inch \approx 2,54cm\) nên chiếc điện thoại theo hình vẽ có : \(\frac{{17}}{{2,54}} \approx 7inch\)
Bài 5. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức: \(M = 5{x^2} + {y^2} + 2x\left( {y - 2} \right) + 8\)
Phương pháp
Phân tích biểu thức thành các tổng của các biểu thức bậc hai bằng cách sử dụng các hằng đẳng thức đáng nhớ.
Lời giải
Ta có: \(M = 5{x^2} + {y^2} + 2x\left( {y - 2} \right) + 8\)
\(\begin{array}{l} = 5{x^2} + {y^2} + 2xy - 4x + 8\\ = {x^2} + 4{x^2} + {y^2} + 2xy - 4x + 1 + 7\\ = \left( {{x^2} + 2xy + {y^2}} \right) + \left( {4{x^2} - 4x + 1} \right) + 7\\ = {\left( {x + y} \right)^2} + {\left( {2x - 1} \right)^2} + 7\end{array}\)
Vì \(\left\{ \begin{array}{l}{\left( {x + y} \right)^2} \ge 0\\{\left( {2x - 1} \right)^2} \ge 0\end{array} \right.,\forall x \in \mathbb{R}\) nên \({\left( {x + y} \right)^2} + {\left( {2x - 1} \right)^2} + 7 \ge 7,\forall x \in \mathbb{R}\).
Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}x + y = 0\\2x - 1 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x + y = 0\\x = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = - \frac{1}{2}\end{array} \right.\).
Vậy giá trị nhỏ nhất của biểu thức M là 7 khi \(x = \frac{1}{2}\) và \(y = - \frac{1}{2}\).
Tải về
Phần trắc nghiệm (3 điểm)
Câu 1: Trong các biểu thức sau, biểu thức nào không phải đơn thức?
A. \({x^2}y\).
B. \( - 3x{y^2}z\).
C. \({x^2}y + 14x{y^2}\).
D. \(x\).
Câu 2: Thu gọn đa thức \(M = {x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + 8{x^2}y + \frac{2}{3}{x^2}y{z^5}\) ta được
A. \(M = - 7{x^2}y - \frac{1}{3}y\).
B. \(M = 9{x^2}y - \frac{1}{3}y\).
C. \(M = 9{x^2}y + \frac{1}{3}x - \frac{4}{3}{x^2}y{z^5}\).
D. \(M = 9{x^2}y + \frac{1}{3}y\).
Câu 3: Kết quả của phép tính \(5{x^2}\left( {2{x^4} - 1} \right)\) là
A. \(7{x^4} - 1\).
B. \(10{x^4} - 1\).
C. \(10{x^8} - 5{x^2}\).
D. \(10{x^6} - 5{x^2}\).
Câu 4: Đa thức \({x^2} - 4{y^2}\) phân tích thành nhân tử là
A. \(\left( {x - 4y} \right)\left( {x + 4y} \right)\).
B. \(\left( {x - 2y} \right)\left( {x + 2y} \right)\).
C. \({\left( {x - 2y} \right)^2}\).
D. \({\left( {x - 4y} \right)^2}\).
Câu 5: Giá trị của biểu thức \(M = \left( {x - y} \right)\left( {{x^2} + {y^2} + xy} \right)\) tại \(x = 1;y = - 2\) là
A. -7.
B. 7.
C. -9.
D. 9.
Câu 6: Giá trị lớn nhất của biểu thức \(A = - {\left( {x - 3} \right)^2} + 2023\) là
A. 3.
B. 2023.
C. 2248.
D. 2006.
Câu 7: Tất cả các số tự nhiên n để đơn thức \(2{x^n}{y^3}\) chia hết cho đơn thức \(4{x^3}{y^n}\) là :
A. \(n = 3\).
B. \(n \ge 3\).
C. \(n > 3\).
D. \(n \le 3\).
Câu 8: Cho hình hộp chữ nhật có các kích thước (tính theo cm) như hình sau:
Đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật là:
A. \(10ah\).
B. \(6{a^2}h\).
C. \(6{a^2} + 10ah\).
D. \(12{a^2} + 10ah\).
Câu 9: Hình bình hành ABCD có số đo góc A bằng 2 lần số đo góc B. Khi đó số đo góc D là:
A. \({60^0}\).
B. \({120^0}\).
C. \({30^0}\).
D. \({45^0}\).
Câu 10: Hình nào sau đây trong thực tế có dạng hình chóp tam giác đều?
A. Hình a.
B. Hình b.
C. Hình c.
D. Hình d.
Câu 11: Cho hình chóp tam giác đều biết độ dài cạnh đáy là 18cm, trung đoạn của hình chóp là 20cm. Diện tích xung quanh của hình chóp tam giác đều đó là:
A. 540 cm2.
B. 1080 cm2.
C. 90 cm2.
D. 180 cm2
Câu 12: Bác Mai muốn may một cái lều cắm trại bằng vải bạt có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2,5m, chiều cao của cái lều trại là 3m. Tính thể tích khoảng không bên trong lều ?

A. \(18,75{m^3}\).
B. \(6,25{m^3}\).
C. \(15{m^3}\).
D. \(9,375{m^3}\).
Phần tự luận (7 điểm)
Bài 1. (1,5 điểm) Phân tích đa thức sau thành nhân tử:
a) \(8x{y^2} - 8xy + 2x\)
b) 25(x+5)2 – 9(x + 7)2
c) 3x2 + 4x – 4
Bài 2. (1,5 điểm)
1)Tìm x, biết:
a) \(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) = 1\)
b) \(3{x^2} + 7x = 10\)
2) Chứng tỏ biểu thức sau không phụ thuộc vào x
A = (x – 3)(x + 2) + (x – 4)(x + 4) – (2x – 1)x
Bài 3. (1 điểm) Một hình chữ nhật có chiều rộng là x (m) và chiều dài là y (m).
a) Viết biểu thức S và biểu thức P lần lượt biểu thị diện tích và chu vi của hình chữ nhật đó.
b) Nếu tăng chiều rộng của hình chữ nhật đó lên 3 lần và giữ nguyên chiều dài thì được một hình chữ nhật mới. Viết biểu thức Pm biểu thị chu vi của hình chữ nhật mới.
Bài 4. (2,5 điểm)
1.Tháp đồng hồ có phần dưới có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh dài 5m, chiều cao của hình hộp chữ nhật là 12m. Phần trên của tháp có dạng hình chóp tứ giác đều, các mặt bên là các tam giác cân chung đỉnh. Chiều cao của tháp đồng hồ là 19,2m.
a) Tính theo mét chiều cao của phần trên của tháp đồng hồ.
b) Tính thể tích của tháp đồng hồ này.
2. Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết 1\(inch \approx 2,54cm\), điện thoại có chiều rộng là 7cm; chiều dài là 15,5 cm. Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch ? (Làm tròn kết quả đến hàng đơn vị ).
Bài 5. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức: \(M = 5{x^2} + {y^2} + 2x\left( {y - 2} \right) + 8\)
- Hết -
Phần trắc nghiệm (3 điểm)
1. C | 2. B | 3. D | 4. B | 5. A | 6. B |
7. A | 8. D | 9. A | 10. C | 11. A | 12. B |
Câu 1: Trong các biểu thức sau, biểu thức nào không phải đơn thức?
A. \({x^2}y\). | B. \( - 3x{y^2}z\). |
C. \({x^2}y + 14x{y^2}\). | D. \(x\). |
Phương pháp
Dựa vào khái niệm đơn thức: Đơn thức là một biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.
Lời giải
Trong các biểu thức trên, chỉ có biểu thức \({x^2}y + 14x{y^2}\) không phải là đơn thức vì có chứa phép cộng.
Đáp án C.
Câu 2: Thu gọn đa thức \(M = {x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + 8{x^2}y + \frac{2}{3}{x^2}y{z^5}\) ta được
A. \(M = - 7{x^2}y - \frac{1}{3}y\). | B. \(M = 9{x^2}y - \frac{1}{3}y\). |
C. \(M = 9{x^2}y + \frac{1}{3}x - \frac{4}{3}{x^2}y{z^5}\). | D. \(M = 9{x^2}y + \frac{1}{3}y\). |
Phương pháp
Cộng, trừ các hạng tử đồng dạng để rút gọn.
Lời giải
\(\begin{array}{l}M = {x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + 8{x^2}y + \frac{2}{3}{x^2}y{z^5}\\ = {x^2}y + 8{x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + \frac{2}{3}{x^2}y{z^5}\\ = ({x^2}y + 8{x^2}y) - \frac{1}{3}y - \left( {\frac{2}{3}{x^2}y{z^5} - \frac{2}{3}{x^2}y{z^5}} \right)\\ = 9{x^2}y - \frac{1}{3}y - 0\\ = 9{x^2}y - \frac{1}{3}y\end{array}\)
Đáp án B.
Câu 3: Kết quả của phép tính \(5{x^2}\left( {2{x^4} - 1} \right)\) là
A. \(7{x^4} - 1\). | B. \(10{x^4} - 1\). |
C. \(10{x^8} - 5{x^2}\). | D. \(10{x^6} - 5{x^2}\). |
Phương pháp
Sử dụng quy tắc nhân đơn thức với đa thức.
Lời giải
\(\begin{array}{l}5{x^2}\left( {2{x^4} - 1} \right) = 5{x^2}.2{x^4} - 5{x^2}.1\\ = \left( {5.2} \right)\left( {{x^2}.{x^4}} \right) - 5{x^2}\\ = 10{x^6} - 5{x^2}\end{array}\)
Đáp án D.
Câu 4: Đa thức \({x^2} - 4{y^2}\) phân tích thành nhân tử là
A. \(\left( {x - 4y} \right)\left( {x + 4y} \right)\). | B. \(\left( {x - 2y} \right)\left( {x + 2y} \right)\). |
C. \({\left( {x - 2y} \right)^2}\). | D. \({\left( {x - 4y} \right)^2}\). |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
\({x^2} - 4{y^2} = \left( {x - 2y} \right)\left( {x + 2y} \right)\).
Đáp án B.
Câu 5: Giá trị của biểu thức \(M = \left( {x - y} \right)\left( {{x^2} + {y^2} + xy} \right)\) tại \(x = 1;y = - 2\) là
A. -7. | B. 7. |
C. -9. | D. 9. |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
\(M = \left( {x - y} \right)\left( {{x^2} + {y^2} + xy} \right) = {x^3} - {y^3}\).
Thay \(x = 1;y = - 2\) vào M, ta được \(M = {1^3} - {\left( { - 2} \right)^3} = 1 - \left( { - 8} \right) = 1 + 8 = 9\).
Đáp án A.
Câu 6: Giá trị lớn nhất của biểu thức \(A = - {\left( {x - 3} \right)^2} + 2023\) là
A. 3. | B. 2023. |
C. 2248. | D. 2006. |
Phương pháp
Dựa vào đặc điểm của bậc chẵn.
Lời giải
Ta có: \({(x - 3)^2} \ge 0 \Leftrightarrow - {(x - 3)^2} \le 0\) với mọi \(x \in \mathbb{R}\) nên \(A = - {\left( {x - 3} \right)^2} + 2023 \le 0 + 2023 = 2023\) với mọi \(x \in \mathbb{R}\).
Dấu bằng xảy ra chính là giá trị lớn nhất của biểu thức A.
Vậy giá trị lớn nhất của biểu thức A là 2023.
Đáp án B.
Câu 7: Tất cả các số tự nhiên n để đơn thức \(2{x^n}{y^3}\) chia hết cho đơn thức \(4{x^3}{y^n}\) là :
A. \(n = 3\). | B. \(n \ge 3\). |
C. \(n > 3\). | D. \(n \le 3\). |
Phương pháp
Để đa thức A chia hết cho đơn thức B thì mọi biến của đa thức A phải có bậc lớn hơn hoặc bằng bậc của các biến trong đơn thức B.
Lời giải
Để đa thức A chia hết cho đơn thức B thì biến x, y trong A phải có bậc lớn hơn hoặc bằng bậc của biến x, y trong B.
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}n \ge 3\\3 \ge n\end{array} \right.\\n = 3\end{array}\)
Suy ra n = 3.
Đáp án A.
Câu 8: Cho hình hộp chữ nhật có các kích thước (tính theo cm) như hình sau:
Đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật là:
A. \(10ah\). | B. \(6{a^2}h\). |
C. \(6{a^2} + 10ah\). | D. \(12{a^2} + 10ah\). |
Phương pháp
Dựa vào công thức tính diện tích hình vuông để viết đa thức.
Lời giải
Tổng diện tích các mặt chính là diện tích toàn phần của hình hộp chữ nhật.
Chu vi đáy: \((3a + 2a).2 = 5a.2 = 10a\)
Diện tích xung quanh: \(10a \cdot h = 10ah.\)
Tổng diện tích hai đáy: \(3a \cdot 2a \cdot 2 = 12{a^2}.\)
Suy ra tổng diện tích các mặt của hình hộp chữ nhật đó là \(S = 12{a^2} + 10ah.\)
Đa thức cần tìm là \(S = 12{a^2} + 10ah.\)
Đáp án D.
Câu 9: Hình bình hành ABCD có số đo góc A bằng 2 lần số đo góc B. Khi đó số đo góc D là:
A. \({60^0}\). | B. \({120^0}\). |
C. \({30^0}\). | D. \({45^0}\). |
Phương pháp
Dựa vào tính chất của hình bình hành và định lí tổng các góc của một tứ giác bằng 3600.
Lời giải
Vì ABCD là hình bình hành nên ta có: \(\widehat A = \widehat C;\widehat B = \widehat D\).
Vì \(\widehat A = 2\widehat B\) nên \(\widehat A + \widehat B + \widehat C + \widehat D = 2\widehat A + 2\widehat B = 2\widehat A + \widehat A = 3\widehat A = {360^0}\)
\( \Rightarrow \widehat A = {120^0} \Rightarrow \widehat B = \widehat D = \frac{{{{120}^0}}}{2} = {60^0}\)
Đáp án A.
Câu 10: Hình nào sau đây trong thực tế có dạng hình chóp tam giác đều?
A. Hình a. | B. Hình b. |
C. Hình c. | D. Hình d. |
Phương pháp
Dựa vào đặc điểm của hình chóp tam giác.
Lời giải
Hình a không phải hình chóp tam giác vì đáy là hình tròn.
Hình b không phải hình chóp tam giác vì đáy là hình vuông.
Hình d không phải hình chóp.
Hình c là hình chóp tam giác vì có 1 đỉnh và đáy là hình tam giác đều.
Đáp án C.
Câu 11: Cho hình chóp tam giác đều biết độ dài cạnh đáy là 18cm, trung đoạn của hình chóp là 20cm. Diện tích xung quanh của hình chóp tam giác đều đó là:
A. 540 cm2. | B. 1080 cm2. |
C. 90 cm2. | D. 180 cm2. |
Phương pháp
Dựa vào công thức thính diện tích xung quanh hình chóp.
Lời giải
Diện tích xung quanh của hình chóp tam giác đều đó là:
\({S_{xq}} = \frac{{18.3}}{2}.20 = 540\left( {c{m^2}} \right)\)
Đáp án A.
Câu 12: Bác Mai muốn may một cái lều cắm trại bằng vải bạt có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2,5m, chiều cao của cái lều trại là 3m. Tính thể tích khoảng không bên trong lều ?

A. \(18,75{m^3}\). | B. \(6,25{m^3}\). |
C. \(15{m^3}\). | D. \(9,375{m^3}\). |
Phương pháp
Dựa vào công thức tính thể tích hình chóp tứ giác đều.
Lời giải
Thể tích khoảng không bên trong lều là :
\(V = \frac{1}{3}.(2,5.2,5).3 = 6,25\,\,\,({m^3})\)
Đáp án B.
Phần tự luận. (7 điểm)
Bài 1. (1,5 điểm) Phân tích đa thức sau thành nhân tử:
a) \(8x{y^2} - 8xy + 2x\)
b) 25(x+5)2 – 9(x + 7)2
c) 3x2 + 4x – 4
Phương pháp
Sử dụng các hằng đẳng thức đáng nhớ để phân tích đa thức.
Lời giải
a) \(8x{y^2} - 8xy + 2x\)
\(\begin{array}{l} = 2x\left( {4{y^2} - 4y + 1} \right)\\ = 2x{\left( {2y - 1} \right)^2}\end{array}\)
b) \(25{\left( {x + 5} \right)^2}-{\rm{ }}9{\left( {x{\rm{ }} + {\rm{ }}7} \right)^2}\)
\(\begin{array}{l} = {\left[ {5\left( {x + 5} \right)} \right]^2}-{\rm{ }}{\left[ {3\left( {x{\rm{ }} + {\rm{ }}7} \right)} \right]^2}\\ = \left[ {5\left( {x + 5} \right) - 3\left( {x + 7} \right)} \right]\left[ {5\left( {x + 5} \right) + 3\left( {x + 7} \right)} \right]\\ = \left( {5x + 25 - 3x - 21} \right)\left( {5x + 25 + 3x + 21} \right)\\ = \left( {2x + 4} \right)\left( {8x + 46} \right)\\ = 2\left( {x + 2} \right).2\left( {4x + 23} \right)\\ = 4\left( {x + 2} \right)\left( {4x + 23} \right)\end{array}\)
c) 3x2 + 4x – 4
\(\begin{array}{l}3{x^2} + 6x - 2x-4\\ = 3x\left( {x + 2} \right) - 2\left( {x + 2} \right)\\ = \left( {x + 2} \right)\left( {3x - 2} \right)\end{array}\)
Bài 2. (1,5 điểm)
1)Tìm x, biết:
a) \(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) = 1\)
b) \(3{x^2} + 7x = 10\)
2) Chứng tỏ biểu thức sau không phụ thuộc vào x
A = (x – 3)(x + 2) + (x – 4)(x + 4) – (2x – 1)x
Phương pháp
1) Sử dụng các phương pháp phân tích đa thức để tìm x.
2) Rút gọn biểu thức để chứng minh biểu thức không phụ thuộc vào x.
Lời giải
a) \(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) = 1\)
\(\begin{array}{l}{x^3} - {3^3} - {x^3} + 4x - 1 = 0\\4x - 28 = 0\\4x = 28\\x = 7\end{array}\)
Vậy x = 7.
b) \(3{x^2} + 7x = 10\)
\(\begin{array}{l}3{x^2} + 7x - 10 = 0\\\left( {3{x^2} - 3} \right) + \left( {7x - 7} \right) = 0\\3\left( {{x^2} - 1} \right) + 7\left( {x - 1} \right) = 0\\3\left( {x - 1} \right)\left( {x + 1} \right) + 7\left( {x - 1} \right) = 0\\\left( {x - 1} \right)\left( {3x + 3 + 7} \right) = 0\\\left( {x - 1} \right)\left( {3x + 10} \right) = 0\\\left[ \begin{array}{l}x - 1 = 0\\3x + 10 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 1\\x = - \frac{{10}}{3}\end{array} \right.\end{array}\)
Vậy x = 1 hoặc x = \( - \frac{{10}}{3}\).
2) A = (x – 3)(x + 2) + (x – 4)(x + 4) – (2x – 1)x
= x2 – 3x + 2x – 6 + x2 – 16 – 2x2 + x
= (x2 + x2 – 2x2) + (-3x + 2x + x) + (-6 – 16)
= 0 + 0 – 22
= - 22.
Vậy A không phụ thuộc vào x.
Bài 3. (1 điểm) Một hình chữ nhật có chiều rộng là x (m) và chiều dài là y (m).
a) Viết biểu thức S và biểu thức P lần lượt biểu thị diện tích và chu vi của hình chữ nhật đó.
b) Nếu tăng chiều rộng của hình chữ nhật đó lên 3 lần và giữ nguyên chiều dài thì được một hình chữ nhật mới. Viết biểu thức Pm biểu thị chu vi của hình chữ nhật mới.
Phương pháp
a) Sử dụng công thức tính diện tích và chu vi của hình chữ nhật để viết biểu thức.
b) Biểu diễn chiều rộng của hình chữ nhật mới theo chiều rộng của hình chữ nhật cũ và tính chu vi hình chữ nhật mới.
Lời giải
a) Công thức biểu thị diện tích hình chữ nhật là: S = x.y (m2).
Công thức biểu thị chu vi của hình chữ nhật là: P = 2(x + y) (m).
b) Chiều rộng của hình chữ nhật mới là: 3x (m).
Chu vi của hình chữ nhật mới là 2(3x + y) = 6x + 2y (m).
Vậy Pm = 6x + 2y.
Bài 4. (2,5 điểm)
1.Tháp đồng hồ có phần dưới có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh dài 5m, chiều cao của hình hộp chữ nhật là 12m. Phần trên của tháp có dạng hình chóp tứ giác đều, các mặt bên là các tam giác cân chung đỉnh. Chiều cao của tháp đồng hồ là 19,2m.
a) Tính theo mét chiều cao của phần trên của tháp đồng hồ.
b) Tính thể tích của tháp đồng hồ này.
2. Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết 1\(inch \approx 2,54cm\), điện thoại có chiều rộng là 7cm; chiều dài là 15,5 cm. Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch ? (Làm tròn kết quả đến hàng đơn vị ).
Phương pháp
1. a) Chiều cao phần trên của tháp đồng hồ bằng chiều cao của tháp đồng hồ - chiều cao hình hộp chữ nhật.
b) Tính thể tích phần hình chóp tứ giác đều + thể tích phần hình hộp chữ nhật ta được thể tích của tháp đồng hồ này.
2. Sử dụng định lí Pythagore.
Lời giải
1.
a) Chiều cao của phần trên của tháp đồng hồ là : 19,2 – 12 = 7,2 (m).
b) Thể tích của phần trên của tháp là : \({V_1} = \frac{1}{3}S.h = \frac{1}{3}{.5^2}.7,2 = 60{m^3}\)
Thể tích của phần dưới của tháp là : \({V_2} = S.h = 5.5.12 = 300{m^3}\).
Thể tích của tháp đồng hồ đó là : \(V = {V_1} + {V_2} = 60 + 300 = 360{m^3}\)
2. Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có :
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2}\\ \Rightarrow BC = \sqrt {A{C^2} + A{B^2}} = \sqrt {{{(15,5)}^2} + {{(7)}^2}} \approx 17(cm)\end{array}\)
Vì \(1\,inch \approx 2,54cm\) nên chiếc điện thoại theo hình vẽ có : \(\frac{{17}}{{2,54}} \approx 7inch\)
Bài 5. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức: \(M = 5{x^2} + {y^2} + 2x\left( {y - 2} \right) + 8\)
Phương pháp
Phân tích biểu thức thành các tổng của các biểu thức bậc hai bằng cách sử dụng các hằng đẳng thức đáng nhớ.
Lời giải
Ta có: \(M = 5{x^2} + {y^2} + 2x\left( {y - 2} \right) + 8\)
\(\begin{array}{l} = 5{x^2} + {y^2} + 2xy - 4x + 8\\ = {x^2} + 4{x^2} + {y^2} + 2xy - 4x + 1 + 7\\ = \left( {{x^2} + 2xy + {y^2}} \right) + \left( {4{x^2} - 4x + 1} \right) + 7\\ = {\left( {x + y} \right)^2} + {\left( {2x - 1} \right)^2} + 7\end{array}\)
Vì \(\left\{ \begin{array}{l}{\left( {x + y} \right)^2} \ge 0\\{\left( {2x - 1} \right)^2} \ge 0\end{array} \right.,\forall x \in \mathbb{R}\) nên \({\left( {x + y} \right)^2} + {\left( {2x - 1} \right)^2} + 7 \ge 7,\forall x \in \mathbb{R}\).
Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}x + y = 0\\2x - 1 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x + y = 0\\x = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = - \frac{1}{2}\end{array} \right.\).
Vậy giá trị nhỏ nhất của biểu thức M là 7 khi \(x = \frac{1}{2}\) và \(y = - \frac{1}{2}\).
Kỳ thi giữa học kỳ 1 Toán 8 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh. Việc làm quen với cấu trúc đề thi và các dạng bài tập thường xuất hiện là yếu tố then chốt để đạt kết quả tốt. Đề thi giữa kì 1 Toán 8 - Đề số 4 mà giaitoan.edu.vn cung cấp là một tài liệu ôn tập lý tưởng, được thiết kế để giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Đề thi này bao gồm các chủ đề chính sau:
Đề thi được chia thành các phần:
Để giải đề thi này một cách hiệu quả, học sinh cần:
Bài toán: Phân tích đa thức sau thành nhân tử: x2 - 4x + 4
Giải:
x2 - 4x + 4 = (x - 2)2
Ngoài việc luyện tập với đề thi, học sinh nên:
Đề thi giữa kì 1 Toán 8 - Đề số 4 của giaitoan.edu.vn là một công cụ hỗ trợ học tập hiệu quả, giúp học sinh chuẩn bị tốt nhất cho kỳ thi. Hãy luyện tập thường xuyên và áp dụng những kiến thức đã học để đạt kết quả cao nhất!