Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 9, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn bám sát chương trình học, đảm bảo tính chính xác và cập nhật.
Đề thi này bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, giúp học sinh rèn luyện kỹ năng giải quyết vấn đề và áp dụng kiến thức đã học vào thực tế.
Các số lần lượt cần điền vào dấu “?” trong bảng sau là gì?

1;4.
4;4.
1;1.
4;1.
Hệ số a, b trong hàm số bậc nhất \(y = 4x - 7\) lần lượt là
\(4x; - 7\).
\(4x;7\).
\(4;7\).
\(4; - 7\).
Một ô tô cách thành phố Hồ Chí Minh 50km. Ô tô bắt đầu đi trên một con đường về phía ngược hướng với thành phố (hình vẽ) với vận tốc là 60km/h. Sau x giờ ô tô cách thành phố Hồ Chí Minh y km. Biểu diễn y theo x.

\(y = 50x\).
\(y = 60x\).
\(y = 60x + 50\).
\(y = 50x + 60\).
Điểm nào sau đây thuộc đồ thị hàm số \(y = 2x - 4\).
\(M\left( {0; - 4} \right)\).
\(N\left( {0;4} \right)\).
\(P\left( {4;0} \right)\).
\(Q\left( { - 4;0} \right)\).
Cho mặt phẳng tọa độ \(Oxy\) và điểm A (như hình vẽ).
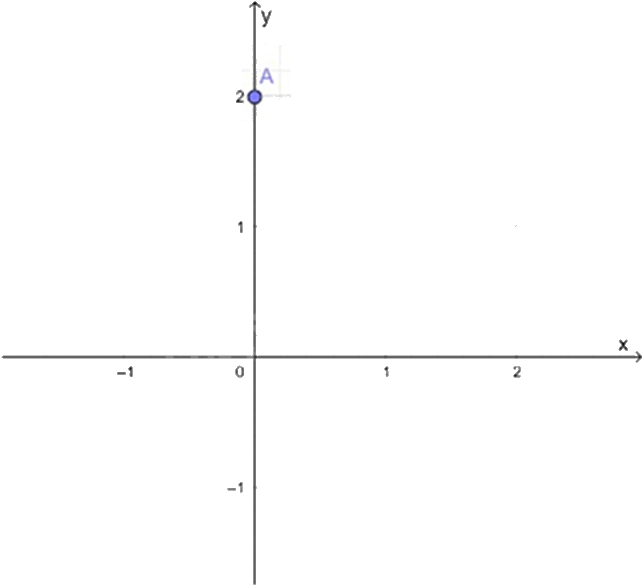
Khi đó tọa độ của điểm A là:
\((0;0)\).
\((2;2)\).
\((2;0)\).
\((0;2)\).
Hệ số góc của đường thẳng \(y = \frac{{2x + 1}}{2}\) là
1.
2.
\(2x\).
\(\frac{1}{2}\).
Cho hình vẽ: Đoạn thẳng nào là đường trung bình của tam giác ABC?
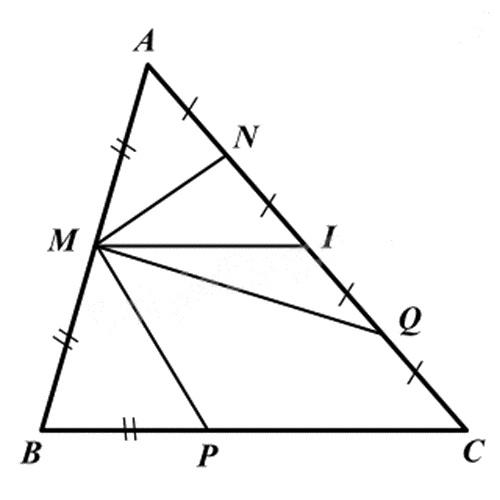
MP.
MN.
MI.
MQ.
Cho tam giác \(\Delta ABC\) vuông tại \(A\), biết\(AB = 6\;{\rm{cm}}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB,AC\) và \(MN = 5\;{\rm{cm}}\). Khi đó, độ dài \(AC\) là:
\(10\;{\rm{cm}}\).
\(3\;{\rm{cm}}\).
\(8\;{\rm{cm}}\).
\(11\;{\rm{cm}}\).
Một cột đèn cao \(10\;{\rm{m}}\) chiếu sáng một cây xanh (như hình vẽ). Cây cách cột đèn \(2m\) và có bóng trải dài dưới mặt đất là\(4,8\;{\rm{m}}\). Tìm chiều cao của cây xanh đó (làm tròn đến mét).
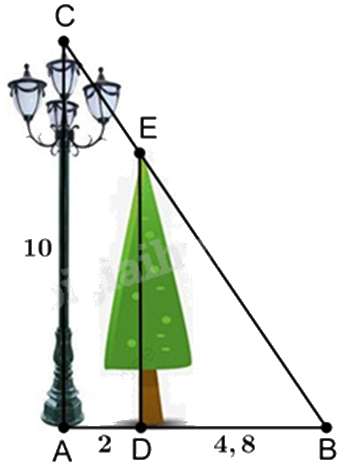
Khi đó, chiều cao của cây xanh là (làm tròn đến mét):
\(DE \approx 14\;{\rm{m}}\).
\(DE \approx 5m\).
\(DE \approx 24m\).
\(DE \approx 7m\).
Cho \(\Delta ABC\) có \(AB = 4cm;AC = 9cm\). Gọi AD là tia phân giác của \(\widehat {BAC}\) . Tính tỉ số \(\frac{{CD}}{{BD}}\).
\(\frac{9}{4}\).
\(\frac{4}{9}\).
\(\frac{4}{5}\).
\(\frac{5}{4}\).
Cho \(\Delta ABC\), tia phân giác góc trong của góc A cắt BC tại D. Cho \(AB = 6\), \(AC = x,BD = 9\),\(BC = 21\). Tính kết quả đúng của độ dài cạnh x?
\(x = 14\).
\(x = 6\).
\(x = 12\).
\(x = 8\).
Tìm x trong hình sau:
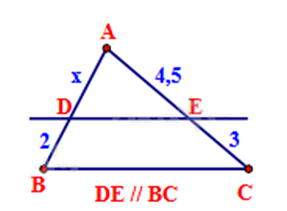
x = 4,5.
x = 3.
x = 1,33.
x = 6,75.
Cho hàm số \(y = \left( {2 - m} \right)x + 1\)
a) Với \(m = 1\) thì đồ thị hàm số song song với đường thẳng \(y = x\).
b) Đồ thị hàm số với \(m = 1\) là:
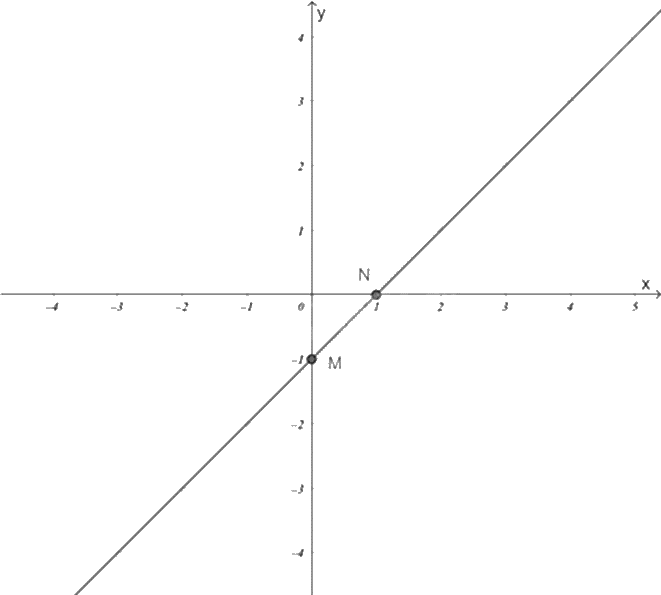
c) Giao điểm A của đồ thị hàm số với \(m = 1\) và \(y = - x + 3\) là \(A\left( {1;2} \right)\).
d) Diện tích của tam giác OAB, với B là giao điểm của đồ thị hàm số \(y = - x + 3\) với trục Ox là 3.
Cho tam giác ABC vuông tại A có AB = 6cm. AC = 8cm. M, N là trung điểm của AB , AC. Vẽ AD là tia phân giác của góc A trong tam giác ABC (D thuộc BC).
a) BC = 10cm.
b) MN = 4cm.
c) \(BD \approx 4,5\)cm.
d) \(BD.AN = AM.DC\).
Hàm số \(y = f\left( x \right)\) được xác định bởi công thức \(y = f\left( x \right) = 3\sqrt x + 5\). Khi đó \(f\left( {\frac{1}{9}} \right)\) là
Đáp án:
Biết khi \(x = 3\) thì hàm số \(y = 2x + b\) có giá trị bằng 4. Giá trị của b là
Đáp án:
Cho tam giác \(ABC\), đường trung tuyến \(AD\). Gọi \(M\) là một điểm trên cạnh \(AC\) sao cho \(AM = \frac{1}{2}MC\). Gọi \(O\) là giao điểm của \(BM\) và \(AD\). \(BM\) bằng bao nhiêu lần \(OM\).
Đáp án:
Gọi đồ thị hàm số \(y = 4x + 2\) là đường thẳng \({d_1}\). Cho hai đường thẳng \({d_2}:y = x - 1\) và \({d_3}:y = \left( {6 - 2m} \right)x\). Tìm m để 3 đường thẳng \({d_1},{d_2},{d_3}\) đồng quy.
Đáp án:
a) Vẽ đồ thị hàm số \(y = - x\) và \(y = x + 3\) trên cùng một mặt phẳng toạ độ.
b) Cho hai hàm số bậc nhất \(y = \left( {m + 5} \right)x - 3\) và \(y = 2x + 1\). Với giá trị nào của m thì đồ thị của hai hàm số đã cho là hai đường thẳng cắt nhau.
a) Cho tam giác ABC có AB = 6 cm, AC = 8 cm. Đường phân giác của góc A cắt BC tại D. Biết DB = 3 cm. Tính DC.
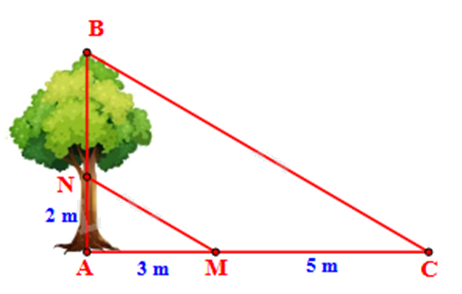
b) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong hình vẽ bên. Tìm chiều cao AB của cây.
Các số lần lượt cần điền vào dấu “?” trong bảng sau là gì?

1;4.
4;4.
1;1.
4;1.
Đáp án : A
Thay giá trị \(x\) vào hàm số để tính giá trị của \(y\) tương ứng.
Với \(x = 0\), \(y = 3.0 + 1 = 1\).
Với \(x = 1\), \(y = 3.1 + 1 = 4\).
Đáp án A
Hệ số a, b trong hàm số bậc nhất \(y = 4x - 7\) lần lượt là
\(4x; - 7\).
\(4x;7\).
\(4;7\).
\(4; - 7\).
Đáp án : D
Hàm số bậc nhất \(y = ax + b\) với hệ số a, b tương ứng.
Hàm số bậc nhất \(y = 4x - 7\) có \(a = 4;b = - 7\).
Đáp án D
Một ô tô cách thành phố Hồ Chí Minh 50km. Ô tô bắt đầu đi trên một con đường về phía ngược hướng với thành phố (hình vẽ) với vận tốc là 60km/h. Sau x giờ ô tô cách thành phố Hồ Chí Minh y km. Biểu diễn y theo x.

\(y = 50x\).
\(y = 60x\).
\(y = 60x + 50\).
\(y = 50x + 60\).
Đáp án : C
Vì ô tô đi về phía ngược hướng thành phố nên khoảng cách giữa ô tô và thành phố Hồ Chí Minh bằng khoảng cách ban đầu + quãng đường ô tô đi được.
Quãng đường = vận tốc x thời gian.
Quãng đường ô tô đi được trong x giờ là:
\(60x\left( {km} \right)\)
Sau x giờ ô tô cách thành phố Hồ Chí Minh là:
\(y = 50 + 60x = 60x + 50\)
Đáp án C
Điểm nào sau đây thuộc đồ thị hàm số \(y = 2x - 4\).
\(M\left( {0; - 4} \right)\).
\(N\left( {0;4} \right)\).
\(P\left( {4;0} \right)\).
\(Q\left( { - 4;0} \right)\).
Đáp án : A
Thay toạ độ điểm vào hàm số xem có thoả mãn không.
Thay \(x = 0\) vào \(y = 2x - 4\), ta được: \(y = 2.0 - 4 = - 4\) nên \(M\left( {0; - 4} \right)\) thuộc đồ thị hàm số \(y = 2x - 4\), \(N\left( {0;4} \right)\) thuộc đồ thị hàm số \(y = 2x - 4\).
Kiểm tra tương tự với P, Q.
Đáp án A
Cho mặt phẳng tọa độ \(Oxy\) và điểm A (như hình vẽ).
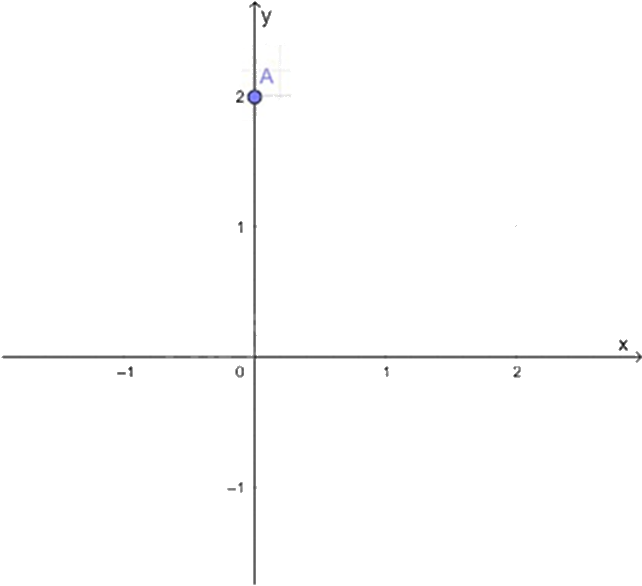
Khi đó tọa độ của điểm A là:
\((0;0)\).
\((2;2)\).
\((2;0)\).
\((0;2)\).
Đáp án : D
Quan sát đồ thị để trả lời.
Điểm A nằm trên trục tung, có hoành độ là 2 nên A(0;2).
Đáp án D
Hệ số góc của đường thẳng \(y = \frac{{2x + 1}}{2}\) là
1.
2.
\(2x\).
\(\frac{1}{2}\).
Đáp án : A
Hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) là a.
Ta có: \(y = \frac{{2x + 1}}{2} = x + \frac{1}{2}\).
Vậy hệ số góc của đường thẳng là 1.
Đáp án A
Cho hình vẽ: Đoạn thẳng nào là đường trung bình của tam giác ABC?
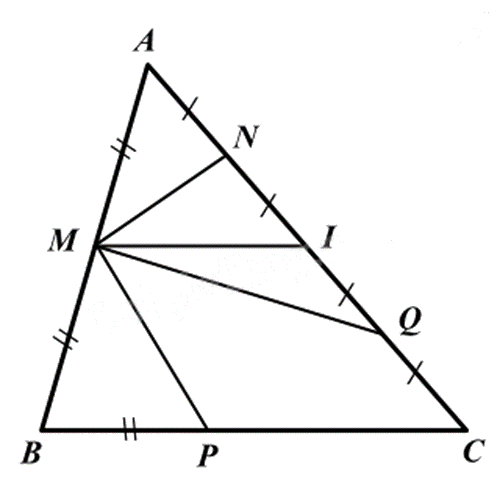
MP.
MN.
MI.
MQ.
Đáp án : C
Dựa vào khái niệm đường trung bình của tam giác: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Vì AN = NI = IQ = IC nên AN + NI = IQ + QC hay AI = IC
Xét tam giác ABC có:
AM = MB, AI = IC (M \( \in \) AB, I \( \in \) AC)
nên MI là đường trung bình của tam giác ABC.
Đáp án C
Cho tam giác \(\Delta ABC\) vuông tại \(A\), biết\(AB = 6\;{\rm{cm}}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB,AC\) và \(MN = 5\;{\rm{cm}}\). Khi đó, độ dài \(AC\) là:
\(10\;{\rm{cm}}\).
\(3\;{\rm{cm}}\).
\(8\;{\rm{cm}}\).
\(11\;{\rm{cm}}\).
Đáp án : C
Chứng minh MN là đường trung bình của tam giác để suy ra BC.
Áp dụng định lí Pythagore vào tam giác vuông ABC để tính AC.
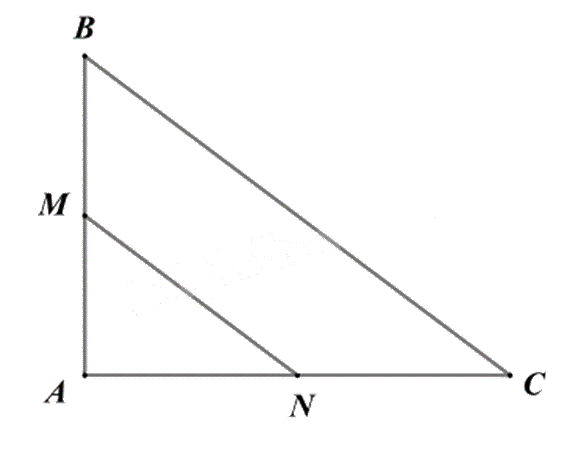
Xét tam giác ABC có:
\(M,N\) lần lượt là trung điểm của \(AB,AC\) nên MN là đường trung bình của tam giác ABC.
Do đó \(MN = \frac{1}{2}BC\), suy ra \(BC = 2MN = 2.5 = 10\left( {cm} \right)\)
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
suy ra \(A{C^2} = B{C^2} - A{B^2} = {10^2} - {6^2} = 64\), suy ra \(AC = \sqrt {64} = 8\left( {cm} \right)\)
Đáp án C
Một cột đèn cao \(10\;{\rm{m}}\) chiếu sáng một cây xanh (như hình vẽ). Cây cách cột đèn \(2m\) và có bóng trải dài dưới mặt đất là\(4,8\;{\rm{m}}\). Tìm chiều cao của cây xanh đó (làm tròn đến mét).
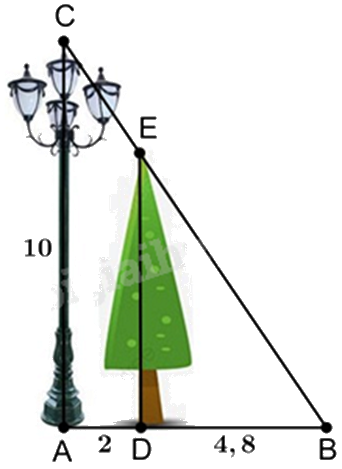
Khi đó, chiều cao của cây xanh là (làm tròn đến mét):
\(DE \approx 14\;{\rm{m}}\).
\(DE \approx 5m\).
\(DE \approx 24m\).
\(DE \approx 7m\).
Đáp án : D
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Vì cột đèn và cây xanh cùng vuông góc với mặt đất nên chúng song song với nhau, hay DE // AC.
Suy ra \(\frac{{BD}}{{AB}} = \frac{{DE}}{{AC}}\), hay \(\frac{{BD}}{{AD + DB}} = \frac{{DE}}{{AC}}\)
Thay số: \(\frac{{4,8}}{{2 + 4,8}} = \frac{{DE}}{{10}}\), suy ra \(DE = \frac{{4,8.10}}{{6,8}} \approx 7\left( m \right)\)
Đáp án D
Cho \(\Delta ABC\) có \(AB = 4cm;AC = 9cm\). Gọi AD là tia phân giác của \(\widehat {BAC}\) . Tính tỉ số \(\frac{{CD}}{{BD}}\).
\(\frac{9}{4}\).
\(\frac{4}{9}\).
\(\frac{4}{5}\).
\(\frac{5}{4}\).
Đáp án : A
Sử dụngTính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
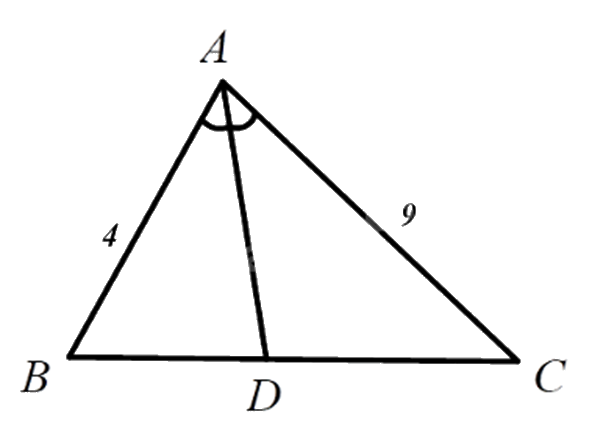
Vì AD là đường phân giác của tam giác ABC nên \(\frac{{CD}}{{BD}} = \frac{{AC}}{{AB}} = \frac{9}{4}\).
Đáp án A
Cho \(\Delta ABC\), tia phân giác góc trong của góc A cắt BC tại D. Cho \(AB = 6\), \(AC = x,BD = 9\),\(BC = 21\). Tính kết quả đúng của độ dài cạnh x?
\(x = 14\).
\(x = 6\).
\(x = 12\).
\(x = 8\).
Đáp án : D
Sử dụngTính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
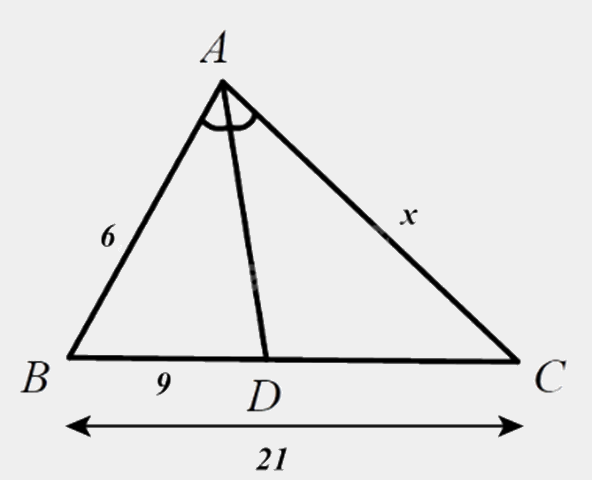
Vì \(D \in BC\) nên \(BD + DC = BC\), suy ra \(CD = BC - BD = 21 - 9 = 12\).
Vì AD là đường phân giác của tam giác ABC nên \(\frac{{AB}}{{AC}} = \frac{{BD}}{{CD}}\).
Thay số: \(\frac{6}{x} = \frac{9}{{12}}\), suy ra \(x = \frac{{6.12}}{9} = 8\).
Đáp án D
Tìm x trong hình sau:
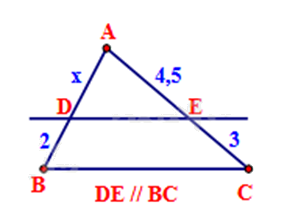
x = 4,5.
x = 3.
x = 1,33.
x = 6,75.
Đáp án : B
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Vì DE // BC nên \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\)
Thay số: \(\frac{x}{2} = \frac{{4,5}}{3}\), suy ra \(x = \frac{{4,5.2}}{3} = 3\).
Đáp án B
Cho hàm số \(y = \left( {2 - m} \right)x + 1\)
a) Với \(m = 1\) thì đồ thị hàm số song song với đường thẳng \(y = x\).
b) Đồ thị hàm số với \(m = 1\) là:
c) Giao điểm A của đồ thị hàm số với \(m = 1\) và \(y = - x + 3\) là \(A\left( {1;2} \right)\).
d) Diện tích của tam giác OAB, với B là giao điểm của đồ thị hàm số \(y = - x + 3\) với trục Ox là 3.
a) Với \(m = 1\) thì đồ thị hàm số song song với đường thẳng \(y = x\).
b) Đồ thị hàm số với \(m = 1\) là:
c) Giao điểm A của đồ thị hàm số với \(m = 1\) và \(y = - x + 3\) là \(A\left( {1;2} \right)\).
d) Diện tích của tam giác OAB, với B là giao điểm của đồ thị hàm số \(y = - x + 3\) với trục Ox là 3.
a) Thay \(m = 1\) vào hàm số. Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song nếu \(a = a',b \ne b'\).
b) Vẽ đồ thị của hàm số để kiểm tra.
c) Tìm tọa độ giao điểm của hai đường thẳng theo các bước:
Bước 1: Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2: Thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số ta tìm được tung độ giao điểm.
d) Xác định độ dài đường cao và cạnh đáy của tam giác OAB để tính diện tích.
a) Đúng
Với \(m = 1\), phương trình trở thành: \(y = \left( {2 - 1} \right)x + 1\) hay \(y = x + 1\).
Vì \(y = x + 1\) và \(y = x\) có \(a = a' = 1\), \(b = 1 \ne 0 = b'\) nên đồ thị hàm số \(y = x + 1\) song song với đường thẳng \(y = x\).
b) Sai
Với \(m = 1\), phương trình trở thành \(y = x + 1\).
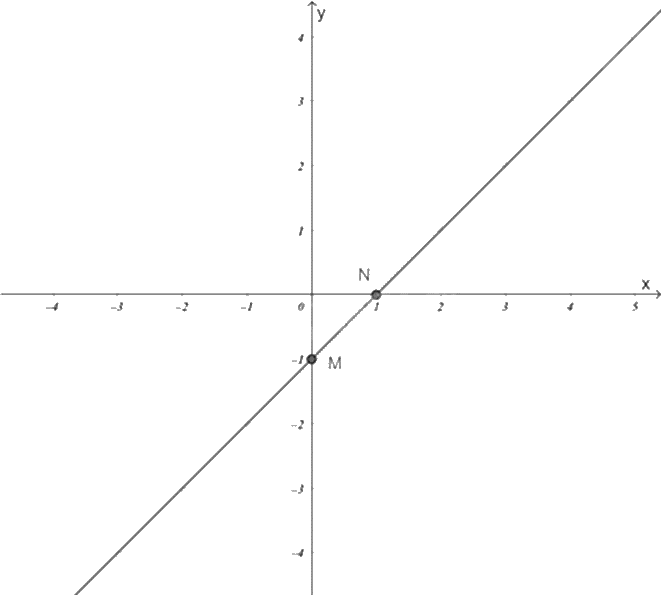
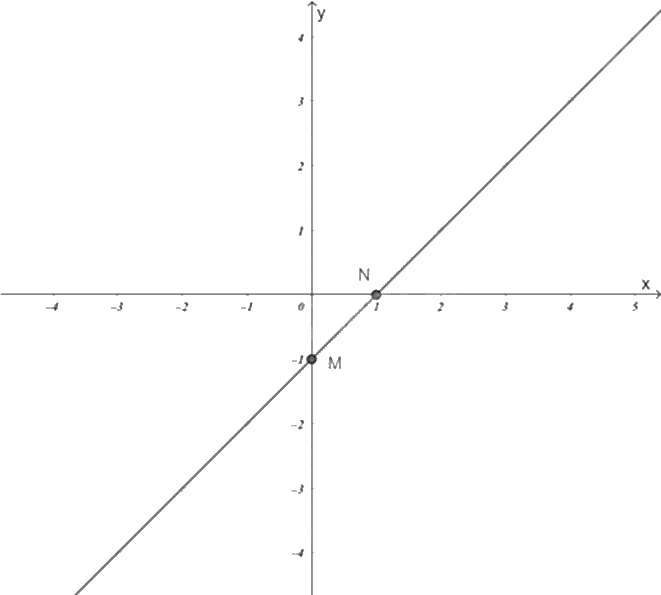
+) Với \(x = 0\) thì \(y = 0 + 1 = 1\) nên đồ thị hàm số đi qua điểm \(M\left( {0;1} \right)\).
+) Với \(y = 0\) thì \(x = 0 - 1 = - 1\) nên đồ thị hàm số đi qua điểm \(N\left( { - 1;0} \right)\).
Đồ thị hàm số \(y = x + 1\) là đường thẳng MN.
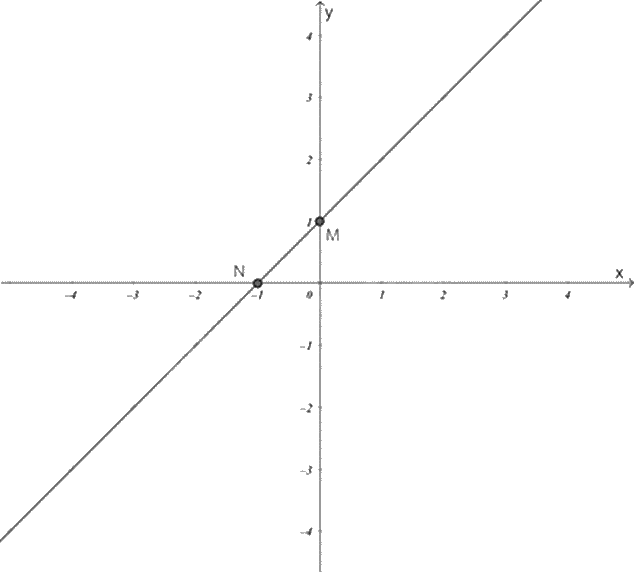
c) Đúng
Xét phương trình hoành độ giao điểm của hai đường thẳng \(y = x + 1\) và \(y = - x + 3\), ta được:
\(\begin{array}{l}x + 1 = - x + 3\\x + x = 3 - 1\\2x = 2\\x = 1\end{array}\)
Khi đó \(y = 1 + 1 = 2\).
Vậy hoành độ giao điểm hai đường thẳng là \(A\left( {1;2} \right)\).
d) Đúng
Biểu diễn đồ thị hàm số \(y = - x + 3\) và \(y = x + 1\) trên cùng một mặt phẳng toạ độ.
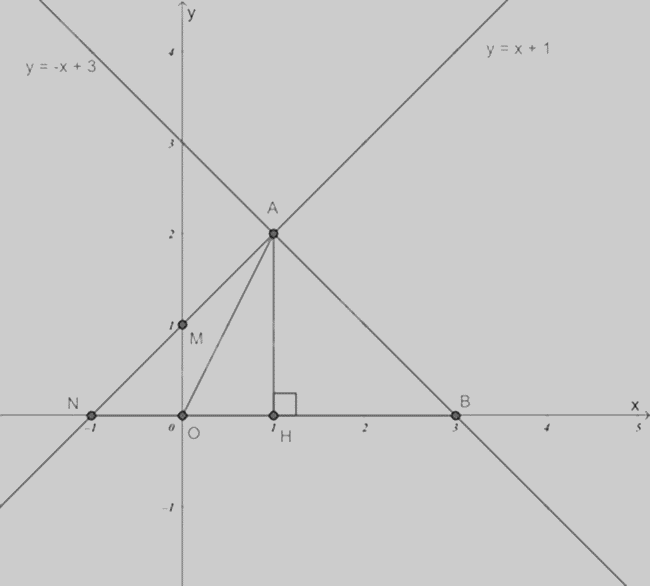
Với \(y = 0\), suy ra \(x = 3\) nên giao điểm của đồ thị hàm số \(y = - x + 3\) với trục Ox là \(B\left( {3;0} \right)\).
Kẻ \(AH \bot Ox\), vì A có tung độ là 2 nên độ dài đoạn AH = 2.
Độ dài đoạn OB là 3.
Khi đó diện tích tam giác OAB là: \({S_{\Delta OAB}} = \frac{1}{2}.AH.OB = \frac{1}{2}.2.3 = 3\).
Đáp án: ĐSĐĐ
Cho tam giác ABC vuông tại A có AB = 6cm. AC = 8cm. M, N là trung điểm của AB , AC. Vẽ AD là tia phân giác của góc A trong tam giác ABC (D thuộc BC).
a) BC = 10cm.
b) MN = 4cm.
c) \(BD \approx 4,5\)cm.
d) \(BD.AN = AM.DC\).
a) BC = 10cm.
b) MN = 4cm.
c) \(BD \approx 4,5\)cm.
d) \(BD.AN = AM.DC\).
a) Áp dụng định lí Pythagore vào tam giác ABC để tính BC.
b) Chứng minh MN là đường trung bình để tính MN.
c) Áp dụng tính chất đường phân giác trong tam giác để tính BD.
d) Kết hợp tính chất đường phân giác trong tam giác và tính chất của trung điểm của AB, AC để kiểm tra khẳng định.
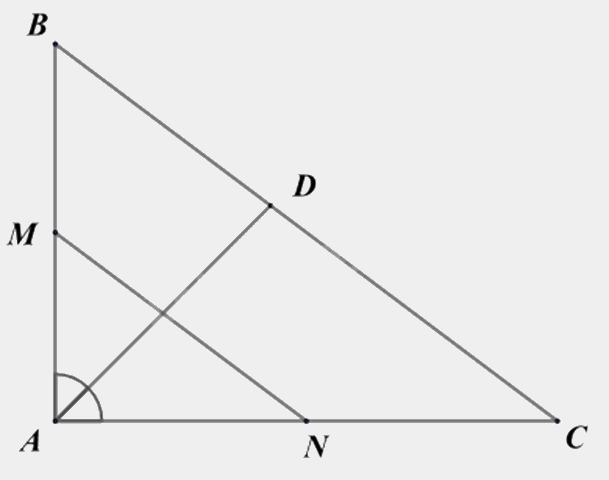
a) Đúng
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = 10\left( {cm} \right)\)
b) Sai
Vì M, N là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC.
Suy ra \(MN = \frac{1}{2}BC = 5\left( {cm} \right)\)
c) Sai
Áp dụng tính chất đường phân giác trong tam giác ABC, ta có:
\(\begin{array}{l}\frac{{BD}}{{AB}} = \frac{{CD}}{{AC}}\\\frac{{BD}}{{AB}} = \frac{{BC - BD}}{{AC}}\\\frac{{BD}}{6} = \frac{{10 - BD}}{8}\\8BD = 6\left( {10 - BD} \right)\\8BD = 60 - 6BD\\14BD = 60\\BD = \frac{{60}}{{14}} \approx 4,3\left( {cm} \right)\end{array}\)
d) Đúng
Theo tính chất đường phân giác trong tam giác ABC, ta có: \(\frac{{BD}}{{AB}} = \frac{{CD}}{{AC}}\)
Kết hợp với \(AB = 2AM,AC = 2AN\) (vì M, N là trung điểm của AB, AC), ta được:
\(\frac{{BD}}{{2AM}} = \frac{{CD}}{{2AN}}\), suy ra \(2AN.BD = 2AM.CD\)
Do đó \(AN.BD = AM.CD\) (chia cả hai vế cho 2).
Đáp án: ĐSSĐ
Hàm số \(y = f\left( x \right)\) được xác định bởi công thức \(y = f\left( x \right) = 3\sqrt x + 5\). Khi đó \(f\left( {\frac{1}{9}} \right)\) là
Đáp án:
Đáp án:
Thay \(x = \frac{1}{9}\) vào hàm số để tính \(f\left( {\frac{1}{9}} \right)\).
Thay giá trị \(x = \frac{1}{9}\) vào công thức hàm số \(y = f\left( x \right) = 3\sqrt x + 5\) ta được:
\(f\left( {\frac{1}{9}} \right) = 3\sqrt {\frac{1}{9}} + 5 = 3\sqrt {{{\left( {\frac{1}{3}} \right)}^2}} + 5 = 3 \cdot \left| {\frac{1}{3}} \right| + 5 = 3 - \frac{1}{3} + 5 = 6\)
Vậy \(f\left( {\frac{1}{9}} \right) = 6\).
Biết khi \(x = 3\) thì hàm số \(y = 2x + b\) có giá trị bằng 4. Giá trị của b là
Đáp án:
Đáp án:
Thay \(x = 3\) và \(y = 4\) vào hàm số \(y = 2x + b\) để tính b.
Thay \(x = 3\) và \(y = 4\) vào hàm số \(y = 2x + b\), ta được: \(4 = 2.3 + b\)
Suy ra \(b = 4 - 2.3 = 4 - 6 = - 2\).
Đáp án: -2
Cho tam giác \(ABC\), đường trung tuyến \(AD\). Gọi \(M\) là một điểm trên cạnh \(AC\) sao cho \(AM = \frac{1}{2}MC\). Gọi \(O\) là giao điểm của \(BM\) và \(AD\). \(BM\) bằng bao nhiêu lần \(OM\).
Đáp án:
Đáp án:
Qua \(D\) vẽ một đường thẳng song song với \(BM\) cắt \(AC\) tại \(N\).
Dựa vào định lí đường trung bình của tam giác để chứng minh \(MN = NC = \frac{1}{2}MC\), \(AM = MN = \frac{1}{2}MC\).
Từ đó chứng minh \(OM\) là đường trung bình của tam giác \(\Delta AND\) nên \(OM = \frac{1}{2}DN\).
\(DN\) là đường trung bình của \(\Delta MBC\) nên \(DN = \frac{1}{2}BM\).
Kết hợp lại để tính được \(BM\) bằng bao nhiêu lần \(OM\).

Qua \(D\) vẽ một đường thẳng song song với \(BM\) cắt \(AC\) tại \(N\).
Xét \(\Delta MBC\) có \(DB = DC\) và \(DN\parallel BM\) nên \(MN = NC = \frac{1}{2}MC\) (định lí đường trung bình của tam giác).
Mặt khác \(AM = \frac{1}{2}MC\) (gt), do đó \(AM = MN = \frac{1}{2}MC\).
Xét \(\Delta AND\) có \(AM = MN\) và \(BM\parallel DN\) nên \(OA = OD\) hay O là trung điểm của AD.
Xét \(\Delta AND\) có:
M là trung điểm của AN (AM = MN), O là trung điểm của AD
nên \(OM\) là đường trung bình nên \(OM = \frac{1}{2}DN\).\(\left( 1 \right)\)
Xét \(\Delta MBC\) có:
N là trung điểm của CM (CN = MN)
D là trung điểm của BC (gt)
nên \(DN\) là đường trung bình nên \(DN = \frac{1}{2}BM\).\(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có: \(OM = \frac{1}{2}DN = \frac{1}{2}.\left( {\frac{1}{2}BM} \right) = \frac{1}{4}BM\) nên \(BM = 4OM\).
Đáp án: 4
Gọi đồ thị hàm số \(y = 4x + 2\) là đường thẳng \({d_1}\). Cho hai đường thẳng \({d_2}:y = x - 1\) và \({d_3}:y = \left( {6 - 2m} \right)x\). Tìm m để 3 đường thẳng \({d_1},{d_2},{d_3}\) đồng quy.
Đáp án:
Đáp án:
Tìm toạ độ giao điểm của \({d_1},{d_2}\) thẳng theo các bước:
Bước 1: Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2: Thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số ta tìm được tung độ giao điểm.
Để 3 đường thẳng \({d_1},{d_2},{d_3}\) đồng quy thì \({d_3}\) cũng đi qua giao điểm của \({d_1},{d_2}\).
Thay toạ độ giao điểm vào \({d_3}\) để tìm m.
Xét phương trình hoành độ giao điểm của \({d_1},{d_2}\), ta có:
\(\begin{array}{l}4x + 2 = x - 1\\4x - x = - 1 - 2\\3x = - 3\\x = - 1\end{array}\)
suy ra \(y = - 1 - 1 = - 2\).
Do đó toạ độ giao điểm của \({d_1},{d_2}\) là \(M\left( { - 1; - 2} \right)\).
Để 3 đường thẳng \({d_1},{d_2},{d_3}\) thì \({d_3}\) phải đi qua điểm \(M\).
Suy ra
\(\begin{array}{l} - 2 = \left( {6 - 2m} \right).\left( { - 1} \right)\\ - 2 = - 6 + 2m\\2m = - 2 + 6\\2m = 4\\m = 2\end{array}\)
Đáp án: 2
a) Vẽ đồ thị hàm số \(y = - x\) và \(y = x + 3\) trên cùng một mặt phẳng toạ độ.
b) Cho hai hàm số bậc nhất \(y = \left( {m + 5} \right)x - 3\) và \(y = 2x + 1\). Với giá trị nào của m thì đồ thị của hai hàm số đã cho là hai đường thẳng cắt nhau.
a) Vẽ đồ thị:
* Trường hợp 1: Xét hàm số \(y = ax\left( {a \ne 0,b = 0} \right)\):
Để vẽ đồ thị hàm số này ta có thể xác định điểm A(1;a) rồi vẽ đường thẳng đi qua hai điểm O và A.
* Trường hợp 2 : Xét hàm số \(y = ax + b\left( {a \ne 0} \right)\):
Để vẽ đồ thị hàm số này ta có thể xác định hai điểm B(0;b) và C\(\left( {\frac{{ - b}}{a};0} \right)\) rồi vẽ đường thẳng đi qua hai điểm đó.
b) Để hai đường thẳng cắt nhau thì \(a \ne a'\).
a) * Vẽ đồ thị hàm số \(y = - x\):
Với \(x = 1\) thì \(y = - 1\), ta được điểm \(A\left( {1; - 1} \right)\).
Vậy đồ thị hàm số \(y = - x\) là đường thẳng \(OA\).
* Vẽ đồ thị hàm số \(y = x + 3\):
Với x = 0 thì y = 3, ta được điểm B(0;3)
Với y = 0 thì x = -3, ta được điểm C(-3;0)
Vậy đồ thị hàm số \(y = x + 3\) là đường thẳng BC.
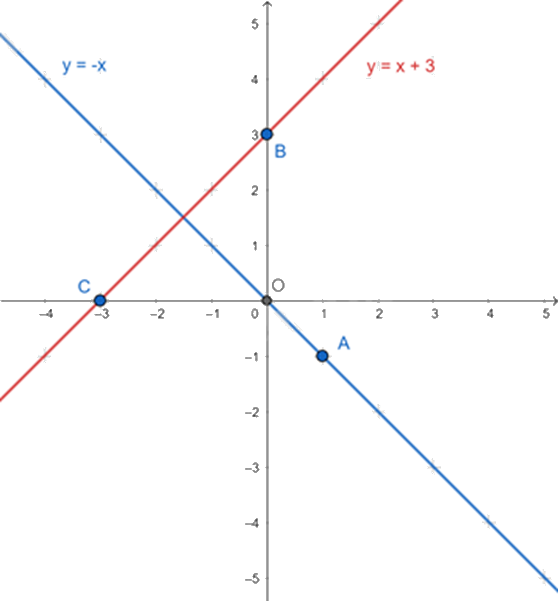
b) Để hai đường thẳng cắt nhau thì \(a \ne a'\)
hay \(m + 5 \ne 2\)
\(m \ne 2 - 5\)
\(m \ne - 3\)
Vậy \(m \ne - 3\) thì đồ thị của hai hàm số đã cho là hai đường thẳng cắt nhau.
a) Cho tam giác ABC có AB = 6 cm, AC = 8 cm. Đường phân giác của góc A cắt BC tại D. Biết DB = 3 cm. Tính DC.
b) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong hình vẽ bên. Tìm chiều cao AB của cây.
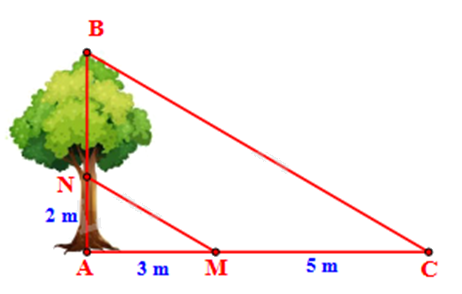
a) Sử dụng tính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
b) Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
a)
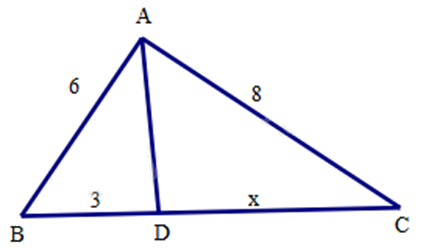
Theo tính chất của đường phân giác, ta có:
\(\begin{array}{l}\frac{{AB}}{{BD}} = \frac{{AC}}{{CD}}\\\frac{6}{3} = \frac{8}{x}\\x = \frac{{8.3}}{6} = 4\end{array}\)
b) Vì tia nắng chiếu song song nên MN // BC.
Áp dụng định lí Thalès với MN // BC, ta có:
\(\begin{array}{l}\frac{{AN}}{{NB}} = \frac{{AM}}{{MC}}\\\frac{2}{{NB}} = \frac{3}{5}\\NB = \frac{{10}}{3}\end{array}\)
Chiều cao AB của cây là: \(AB = AN + NB = 2 + \frac{{10}}{3} = \frac{{16}}{3}\left( m \right)\)
Vậy chiều cao AB của cây là \(\frac{{16}}{3}m\).
Kỳ thi giữa học kỳ 2 Toán 8 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh. Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 9 là một bài kiểm tra được thiết kế để đánh giá mức độ nắm vững kiến thức và kỹ năng của học sinh sau khi học xong các chương trình trong nửa học kỳ. Bài viết này sẽ cung cấp một cái nhìn tổng quan về đề thi, các dạng bài tập thường gặp, và hướng dẫn giải chi tiết để giúp học sinh ôn tập hiệu quả.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi:
Dưới đây là một số dạng bài tập thường gặp trong đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 9:
Ví dụ 1: Giải phương trình 2x + 3 = 7
Lời giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Ví dụ 2: Phân tích đa thức x2 - 4 thành nhân tử
Lời giải:
x2 - 4 = (x - 2)(x + 2)
Ngoài việc luyện tập với đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 9, học sinh có thể tham khảo thêm các tài nguyên sau:
Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 9 là một cơ hội tốt để học sinh đánh giá năng lực và chuẩn bị cho các kỳ thi tiếp theo. Bằng cách ôn tập kỹ lưỡng, nắm vững kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể đạt kết quả tốt nhất trong kỳ thi.