Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 8 Cánh diều - Đề số 10, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 8 Cánh diều, bao gồm các dạng bài tập đa dạng và có độ khó phù hợp.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và áp dụng kiến thức đã học vào thực tế.
Cho các loại dữ liệu sau:
– Học lực của một số bạn học sinh trong lớp: Giỏi, Khá, Đạt, Chưa đạt
– Các loại cây trong một khu vườn: cam, mít, xoài, ổi, táo,...
– Điểm kiểm tra môn Toán của các bạn Hà, Trang, Bình, An: 9, 7, 8, 7
Dữ liệu định lượng trong các dữ liệu trên là:
Học lực của một số bạn học sinh trong lớp.
Các loại cây trong một khu vườn.
Điểm kiểm tra môn Toán của các bạn Hà, Trang, Bình, An.
Không có dữ liệu định lượng trong các dữ liệu trên.
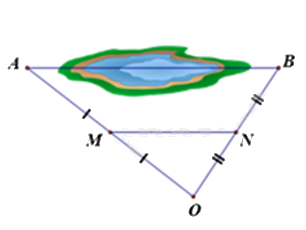
Giữa hai địa điểm A và B là một hồ nước sâu (hình bên). Biết M, N lần lượt là trung điểm của OA và OB, biết khoảng cách M và N là 300m. Tính khoảng cách AB.
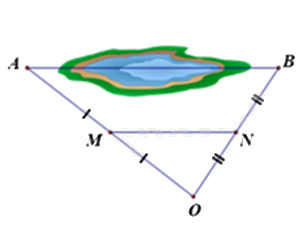
600m.
1200m.
150m.
1000m.
Biết BD là tia phân giác của góc B, tính giá trị của x.
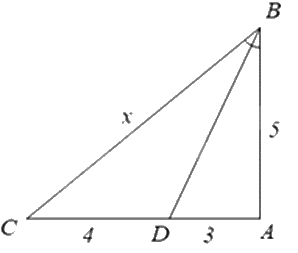
\(\frac{{20}}{3}\).
\(\frac{3}{{20}}\).
\(\frac{{15}}{4}\).
\(\frac{4}{{15}}\).
Nếu $\Delta ABC\backsim \Delta A'B'C'$. theo tỉ số \(k = \frac{1}{3}\) thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số
\(\frac{1}{3}\).
\(\frac{1}{9}\).
\(3\).
\(9\).
Cho $\Delta ABC\backsim \Delta DEF$, biết \(\widehat A = 75^\circ ,\widehat B = 50^\circ \). Khi đó số đo \(\widehat F\) bằng
\(65^\circ \).
\(85^\circ \).
\(55^\circ \).
\(75^\circ \).
Muốn so sánh hai tập dữ liệu với nhau, ta nên chọn biểu đồ nào?
Biểu đồ tranh.
Biểu đồ đoạn thẳng.
Biểu đồ cột kép.
Biểu đồ hình quạt tròn.
Diện tích rừng trồng tập trung của một địa phương từ năm 2018 đến năm 2023 được cho trong bảng sau:

Địa phương trên có diện tích rừng trồng tập trung nhiều nhất vào năm nào?
2021.
2020.
2023.
2022.
Biểu đồ hình quạt tròn (như hình vẽ) biểu diễn tỉ lệ % các loại quả gồm nhãn, táo, lê và nho bán được của 1 cửa hàng. Biết ngày hôm đó cửa hàng bán được 150 kg 4 loại quả trên.
Khẳng định nào sau đây là ĐÚNG?
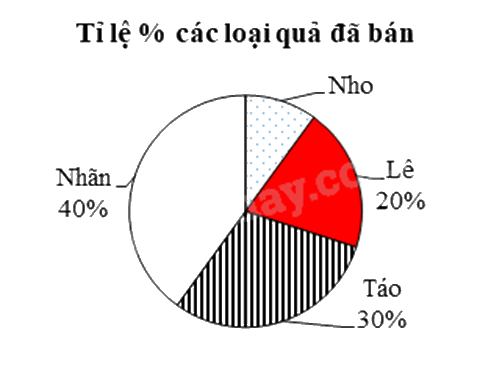
Cửa hàng bán được 30 kg táo.
Khối lượng nhãn bán được nhiều hơn khối lượng nho bán được là 30 kg.
Cửa hàng bán được tổng 45 kg lê và nho.
Khối lượng nhãn bán được là 40 kg.
Tại ứng dụng Shopee tất cả người dùng được quyền tham gia chương trình “Vòng quay Freeship”. Chương trình được mô tả bởi một bánh xe hình tròn chia thành \(6\) hình quạt như nhau, trên mỗi hình quạt có ghi phần quà tương ứng, trong đó có \(3\) hình quạt ghi phần quà là mã Freeship \(15000\) của Shopee (tham khảo hình minh họa dưới đây). Ở mỗi lượt chơi, người chơi sẽ nhấp vào ô “Quay” ở chính giữa vòng quay may mắn. Khi mũi tên trên vòng quay dừng ở hình quạt nào thì người chơi nhận được phần quà ghi trên hình quạt đó. An tham gia chương trình này. Xác suất của biến cố “Trong lượt quay đầu tiên, An nhận được phần quà là mã Freeship \(15000\)” bằng

\(3.\)
\(\frac{1}{2}.\)
\(\frac{1}{3}.\)
\(\frac{1}{6}.\)
Một cửa hàng bán ô tô thống kê màu xe được bán ra trong Quý III năm 2024 như sau:

Chọn ngẫu nhiên một khách hàng đã mua xe trong quý III để trao thưởng. Xác suất của biến cố “Khách hàng được chọn mua xe màu trắng” xấp xỉ
\(0,721\).
\(0,240\).
\(0,227.\)
\(0,279\).
Cho tam giác ABC, biết \({\rm{MN // }}BC\). Trong khẳng định sau, khẳng định nào đúng?
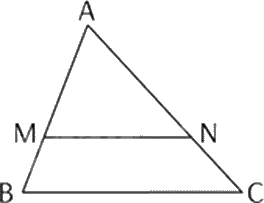
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{AC}}\).
\(\frac{{AN}}{{NC}} = \frac{{MN}}{{BC}}\).
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
\(\frac{{AM}}{{MB}} = \frac{{NC}}{{AN}}\).
Cho hai đoạn thẳng \(MN = 6cm\) và \(PQ = 18\,cm\). Tỉ số của đoạn thẳng MN và PQ là:
\(\frac{2}{3}\).
\(\frac{3}{2}\).
\(\frac{1}{3}\).
\(3\).
Biểu đồ kép (hình bên) biểu diễn số công nhân xếp loại Tốt trong quý III và quý IV của 4 đội công nhân.
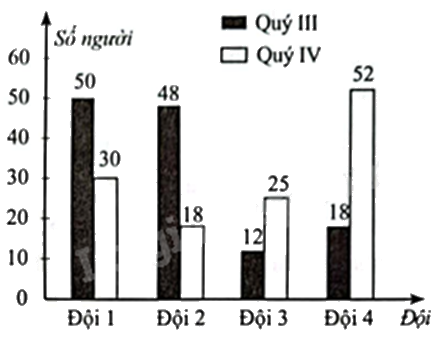
a) Bảng thống kê số công nhân xếp loại Tốt trong quý III và quý IV là:

b) Tổng số công nhân xếp loại tốt của quý III là 128 người.
c) Tổng số công nhân xếp loại Tốt quý IV nhiều hơn so với quý III.
d) Công ty muốn chọn ra 1 công nhân tiêu biểu của quý IV. Xác suất để chọn ra được công nhân tiêu biểu của đội 1 là \(\frac{6}{{25}}\).
Cho tam giác ABC, trung tuyến AM. Các tia phân giác của góc AMB, AMC cắt AB, AC lần lượt tại D và E. Cho BC = 12cm, AM = 8cm, AB = 7cm. Gọi I là giao điểm của DE và AM.
a) \(\frac{{AD}}{{DB}} = \frac{2}{3}\).
b) \(DE//BC\)
c) \(DE = \frac{{36}}{7}\).
d) \(DI = IE\)
Biểu đồ dưới đây cho biết doanh thu 12 tháng của một cửa hàng A.
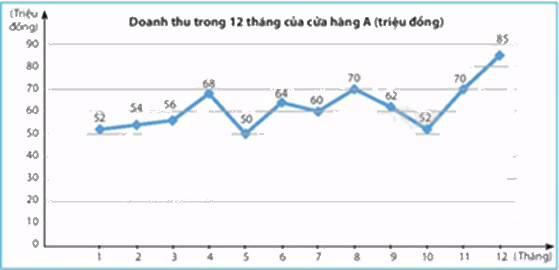
Tính độ chênh lệch giữa doanh thu cao nhất và doanh thu thấp nhất của cửa hàng trên. (đơn vị: triệu đồng)
Đáp án:
Tỉ lệ số học sinh nam của lớp 8A là \(34\% \). Chọn ra ngẫu nhiên một học sinh trong lớp. Xác suất của biến cố “Học sinh được chọn ra là học sinh nữ” là (viết dưới dạng số thập phân).
Đáp án:
Cho tam giác ABC có AB = 9 cm, điểm D thuộc cạnh AB sao AD = 6 cm. Kẻ DE song song với BC (E \( \in \) AC), kẻ EF song song với CD (F \( \in \) AB). Độ dài đoạn thẳng AF bằng bao nhiêu cm?
Đáp án:
Cho tam giác ABC có D, E lần lượt là trung điểm của các cạnh AB, AC và DE = 4cm.Biết đường cao AH = 6cm. Diện tích tam giác ABC là ...\(c{m^2}\).
Đáp án:
Biểu đồ dưới đây biểu diễn tốc độ tăng tổng sản phẩm trong nước (GDP) của nước ta 9 tháng đầu năm 2024 so với cùng kỳ năm trước.
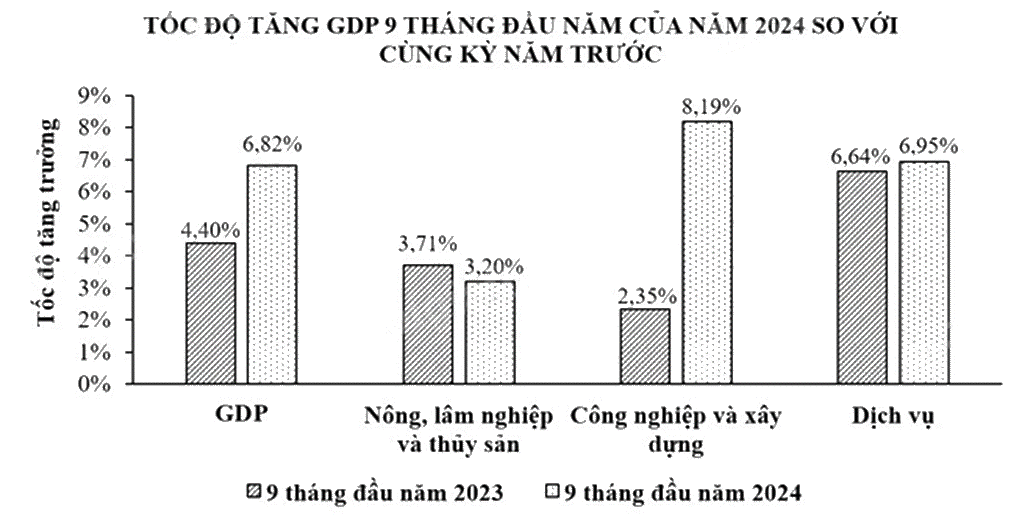
(Nguồn: Tổng cục thống kê)
a) Lập bảng thống kê tốc độ tăng GDP 9 tháng đầu năm 2024 của ba khu vực: Nông, lâm nghiệp và thủy sản; Công nghiệp và xây dựng; Dịch vụ.
b) Tốc độ tăng GDP 9 tháng đầu năm 2024 của khu vực Dịch vụ so với cùng kỳ năm trước tăng hay giảm bao nhiêu %?
c) Với ba khu vực trong bảng thống kê, khu vực nào có tốc độ tăng GDP 9 tháng đầu năm 2024 cao nhất so với cùng kỳ năm trước?
Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm của hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC. Chứng minh:
a) \(\Delta FBA = \Delta FCK\).
b) \(EF = \frac{{AB + CD}}{2}\).
Cho các loại dữ liệu sau:
– Học lực của một số bạn học sinh trong lớp: Giỏi, Khá, Đạt, Chưa đạt
– Các loại cây trong một khu vườn: cam, mít, xoài, ổi, táo,...
– Điểm kiểm tra môn Toán của các bạn Hà, Trang, Bình, An: 9, 7, 8, 7
Dữ liệu định lượng trong các dữ liệu trên là:
Học lực của một số bạn học sinh trong lớp.
Các loại cây trong một khu vườn.
Điểm kiểm tra môn Toán của các bạn Hà, Trang, Bình, An.
Không có dữ liệu định lượng trong các dữ liệu trên.
Đáp án : C
Dữ liệu định lượng là những dữ liệu thống kê là số (số liệu) được biểu diễn bằng số thực.
Học lực không phải là dữ liệu định lượng vì không được biểu diễn bằng số.
Các loại cây không phải là dữ liệu định lượng vì không được biểu diễn bằng số.
Điểm kiểm tra được biểu diễn bằng số nên là dữ liệu định lượng.
Đáp án C
Giữa hai địa điểm A và B là một hồ nước sâu (hình bên). Biết M, N lần lượt là trung điểm của OA và OB, biết khoảng cách M và N là 300m. Tính khoảng cách AB.
600m.
1200m.
150m.
1000m.
Đáp án : A
Sử dụng tính chất của đường trung bình trong tam giác: đường trung bình bằng một nửa cạnh thứ ba.
Vì M, N lần lượt là trung điểm của OA và OB nên MN là đường trung bình của tam giác OAB, khi đó \(MN = \frac{1}{2}AB\).
Do đó khoảng cách AB là:
\(AB = 2MN = 2.300 = 600\left( m \right)\)
Đáp án A
Biết BD là tia phân giác của góc B, tính giá trị của x.
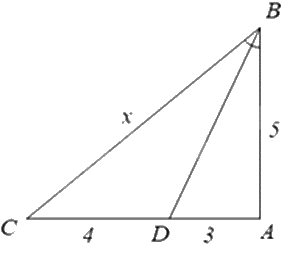
\(\frac{{20}}{3}\).
\(\frac{3}{{20}}\).
\(\frac{{15}}{4}\).
\(\frac{4}{{15}}\).
Đáp án : A
Sử dụngTính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Vì BD là đường phân giác của tam giác ABC nên \(\frac{{BC}}{{BA}} = \frac{{CD}}{{DA}}\).
Thay số: \(\frac{x}{5} = \frac{4}{3}\). Suy ra \(x = \frac{4}{3}.5 = \frac{{20}}{3}\).
Đáp án A
Nếu $\Delta ABC\backsim \Delta A'B'C'$. theo tỉ số \(k = \frac{1}{3}\) thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số
\(\frac{1}{3}\).
\(\frac{1}{9}\).
\(3\).
\(9\).
Đáp án : C
Nếu $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số đồng dạng k thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng $\frac{1}{k}$.
Vì $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số \(k = \frac{1}{3}\) nên $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số \(k' = \frac{1}{k} = 1:\frac{1}{3} = 3\).
Đáp án C
Cho $\Delta ABC\backsim \Delta DEF$, biết \(\widehat A = 75^\circ ,\widehat B = 50^\circ \). Khi đó số đo \(\widehat F\) bằng
\(65^\circ \).
\(85^\circ \).
\(55^\circ \).
\(75^\circ \).
Đáp án : C
Xác định đỉnh tương ứng với đỉnh F trong tam giác ABC. Khi đó \(\widehat F\) bằng với góc ở đỉnh tương ứng của nó trong tam giác ABC.
Sử dụng định lí tổng ba góc trong một tam giác bằng \(180^\circ \) để tính góc còn lại của tam giác ABC.
Vì $\Delta ABC\backsim \Delta DEF$ nên \(\widehat F = \widehat C\).
Xét \(\Delta ABC\) có: \(\widehat A + \widehat B + \widehat C = 180^\circ \).
Suy ra \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 75^\circ - 50^\circ = 55^\circ \).
Đáp án C
Muốn so sánh hai tập dữ liệu với nhau, ta nên chọn biểu đồ nào?
Biểu đồ tranh.
Biểu đồ đoạn thẳng.
Biểu đồ cột kép.
Biểu đồ hình quạt tròn.
Đáp án : C
Dựa vào mục đích sử dụng các loại biểu đồ.
Muốn so sánh hai tập dữ liệu với nhau ta nên sử dụng biểu đồ cột kép.
Đáp án C
Diện tích rừng trồng tập trung của một địa phương từ năm 2018 đến năm 2023 được cho trong bảng sau:

Địa phương trên có diện tích rừng trồng tập trung nhiều nhất vào năm nào?
2021.
2020.
2023.
2022.
Đáp án : C
Quan sát bảng, diện tích rừng trồng tập trung năm nào lớn nhất.
Quan sát bảng ta thấy diện tích năm 2023 là lớn nhất (18 nghìn hecta).
Đáp án C
Biểu đồ hình quạt tròn (như hình vẽ) biểu diễn tỉ lệ % các loại quả gồm nhãn, táo, lê và nho bán được của 1 cửa hàng. Biết ngày hôm đó cửa hàng bán được 150 kg 4 loại quả trên.
Khẳng định nào sau đây là ĐÚNG?
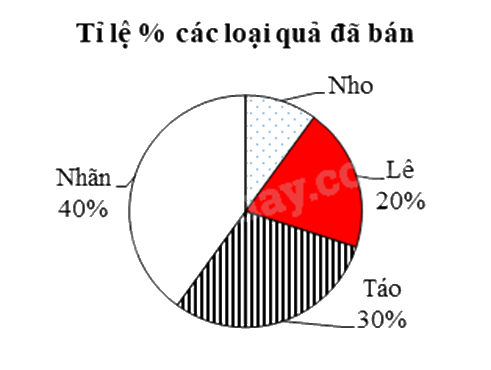
Cửa hàng bán được 30 kg táo.
Khối lượng nhãn bán được nhiều hơn khối lượng nho bán được là 30 kg.
Cửa hàng bán được tổng 45 kg lê và nho.
Khối lượng nhãn bán được là 40 kg.
Đáp án : C
Tính số kg bán được = tỉ lệ %. tổng số kg cửa hàng bán được.
Từ biểu đồ hình quạt tròn trên, ta tính được số kg bán được các loại quả như sau:
Táo: 30%.150 = 45 (kg)
Lê: 20%.150 = 30 (kg)
Nhãn: 40%.150 = 60 (kg)
Nho: (100% - 30% - 20% - 40%).150 = 15 (kg)
Do đó:
+) Táo bán được 30kg nên A sai.
+) Nhãn – Nho = 60 – 15 = 45 (kg) nên B sai.
+) Lê + Nho = 30 + 15 = 45 (kg) nên C đúng.
+) Nhãn bán được 40 kg nên D sai.
Đáp án C
Tại ứng dụng Shopee tất cả người dùng được quyền tham gia chương trình “Vòng quay Freeship”. Chương trình được mô tả bởi một bánh xe hình tròn chia thành \(6\) hình quạt như nhau, trên mỗi hình quạt có ghi phần quà tương ứng, trong đó có \(3\) hình quạt ghi phần quà là mã Freeship \(15000\) của Shopee (tham khảo hình minh họa dưới đây). Ở mỗi lượt chơi, người chơi sẽ nhấp vào ô “Quay” ở chính giữa vòng quay may mắn. Khi mũi tên trên vòng quay dừng ở hình quạt nào thì người chơi nhận được phần quà ghi trên hình quạt đó. An tham gia chương trình này. Xác suất của biến cố “Trong lượt quay đầu tiên, An nhận được phần quà là mã Freeship \(15000\)” bằng

\(3.\)
\(\frac{1}{2}.\)
\(\frac{1}{3}.\)
\(\frac{1}{6}.\)
Đáp án : B
Trong trò chơi vòng quay số, nếu k là số kết quả thuận lợi cho một biến cố và n là số ô của vòng quay thì xác suất của biến cố đó bằng \(\frac{k}{n}\).
Số kết quả thuận lợi cho biến cố “Trong lượt quay đầu tiên, An nhận được phần quà là mã Freeship \(15000\)” là: 3.
Tổng số ô của vòng quay là 6.
Do đó xác suất của biến cố “Trong lượt quay đầu tiên, An nhận được phần quà là mã Freeship \(15000\)” bằng: \(\frac{3}{6} = \frac{1}{2}\).
Đáp án B
Một cửa hàng bán ô tô thống kê màu xe được bán ra trong Quý III năm 2024 như sau:

Chọn ngẫu nhiên một khách hàng đã mua xe trong quý III để trao thưởng. Xác suất của biến cố “Khách hàng được chọn mua xe màu trắng” xấp xỉ
\(0,721\).
\(0,240\).
\(0,227.\)
\(0,279\).
Đáp án : C
Trong trò chơi ngẫu nhiên, một đối tượng từ một nhóm đối tượng, xác suất của một biến cố bằng tỉ số của số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.

Xác suất của biến cố “Khách hàng được chọn mua xe màu trắng” là:
\(\frac{{25}}{{25 + 45 + 23 + 12 + 5}} \approx 0,227\).
Đáp án C
Cho tam giác ABC, biết \({\rm{MN // }}BC\). Trong khẳng định sau, khẳng định nào đúng?
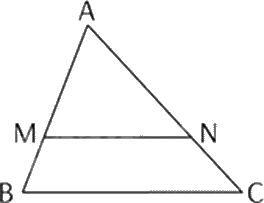
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{AC}}\).
\(\frac{{AN}}{{NC}} = \frac{{MN}}{{BC}}\).
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
\(\frac{{AM}}{{MB}} = \frac{{NC}}{{AN}}\).
Đáp án : C
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Vì \({\rm{MN // }}BC\) nên \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
Đáp án C
Cho hai đoạn thẳng \(MN = 6cm\) và \(PQ = 18\,cm\). Tỉ số của đoạn thẳng MN và PQ là:
\(\frac{2}{3}\).
\(\frac{3}{2}\).
\(\frac{1}{3}\).
\(3\).
Đáp án : C
Tỉ số của đoạn thẳng MN và PQ là \(\frac{{MN}}{{PQ}}\).
Tỉ số của đoạn thẳng MN và PQ là: \(\frac{{MN}}{{PQ}} = \frac{6}{{18}} = \frac{1}{3}\).
Đáp án C
Biểu đồ kép (hình bên) biểu diễn số công nhân xếp loại Tốt trong quý III và quý IV của 4 đội công nhân.
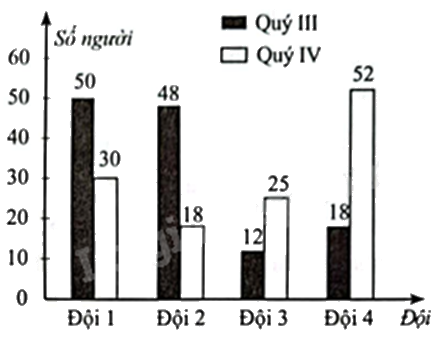
a) Bảng thống kê số công nhân xếp loại Tốt trong quý III và quý IV là:

b) Tổng số công nhân xếp loại tốt của quý III là 128 người.
c) Tổng số công nhân xếp loại Tốt quý IV nhiều hơn so với quý III.
d) Công ty muốn chọn ra 1 công nhân tiêu biểu của quý IV. Xác suất để chọn ra được công nhân tiêu biểu của đội 1 là \(\frac{6}{{25}}\).
a) Bảng thống kê số công nhân xếp loại Tốt trong quý III và quý IV là:

b) Tổng số công nhân xếp loại tốt của quý III là 128 người.
c) Tổng số công nhân xếp loại Tốt quý IV nhiều hơn so với quý III.
d) Công ty muốn chọn ra 1 công nhân tiêu biểu của quý IV. Xác suất để chọn ra được công nhân tiêu biểu của đội 1 là \(\frac{6}{{25}}\).
a) Từ biểu đồ kép so sánh với bảng thống kê.
b) Tính tổng số công nhân của quý III bằng tổng số công nhân 4 đội trong quý III.
c) Tính tổng số công nhân xếp loại Tốt trong Quý III và Quý IV sau đó so sánh.
d) Tính xác suất chọn được nhân viên của đội 1 so với tổng số nhân viên trong quý IV.
a) Sai
Bảng thống kê số công nhân xếp loại Tốt trong quý III và quý IV là:
b) Đúng
Tổng số công nhân xếp loại Tốt của quý III là: 50 + 48 + 12 + 18 = 128 (người)
c) Sai
Tổng số công nhân xếp loại Tốt quý IV là: 30 + 18 + 25 + 52 = 125 (người)
Vì 125 < 128 nên tổng số công nhân xếp loại Tốt quý IV ít hơn so với quý III.
d) Đúng
Xác suất để chọn ra được công nhân tiêu biểu của đội 1 trong quý IV là: \(\frac{{30}}{{125}} = \frac{6}{{25}}\).
Đáp án: SĐSĐ
Cho tam giác ABC, trung tuyến AM. Các tia phân giác của góc AMB, AMC cắt AB, AC lần lượt tại D và E. Cho BC = 12cm, AM = 8cm, AB = 7cm. Gọi I là giao điểm của DE và AM.
a) \(\frac{{AD}}{{DB}} = \frac{2}{3}\).
b) \(DE//BC\)
c) \(DE = \frac{{36}}{7}\).
d) \(DI = IE\)
a) \(\frac{{AD}}{{DB}} = \frac{2}{3}\).
b) \(DE//BC\)
c) \(DE = \frac{{36}}{7}\).
d) \(DI = IE\)
a) Vì AM là đường trung tuyến M là trung điểm của BC. Ta tính được BM, CM theo BC.
Áp dụng tính chất của đường phân giác trong tam giác để tính \(\frac{{AD}}{{DB}}\)
b) Áp dụng tính chất của đường phân giác trong tam giác để tính được tỉ số \(\frac{{AE}}{{EC}}\).
Kết hợp với tỉ số \(\frac{{AD}}{{DB}}\) và định lí Thalès đảo để kiểm tra DE // BC.
c) Sử dụng tính chất của dãy tỉ số bằng nhau để tính AD.
Áp dụng hệ quả của định lí Thalès ta tính được DE.
d) Sử dụng hệ quả của định lí Thalès với DI // BM, IE // MC để kiểm tra DI = IE.
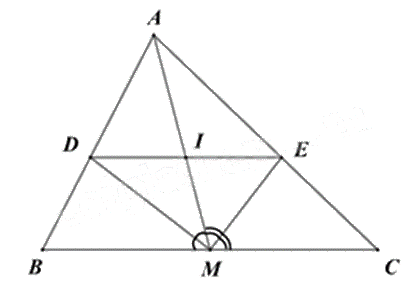
a) Sai
Vì AM là đường trung tuyến nên M là trung điểm của BC, suy ra \(BM = MC = \frac{1}{2}BC = \frac{1}{2}.12 = 6\left( {cm} \right)\). (1)
Vì MD là đường phân giác của tam giác ABM nên \(\frac{{AD}}{{DB}} = \frac{{AM}}{{BM}} = \frac{8}{6} = \frac{4}{3}\). (2)
b) Đúng
Vì ME là đường phân giác của tam giác ACM nên \(\frac{{AE}}{{EC}} = \frac{{AM}}{{MC}}\). (3)
Từ (1), (2) và (3) suy ra \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) nên DE // BC (Định lí Thalès đảo)
c) Sai
Vì \(\frac{{AD}}{{DB}} = \frac{4}{3}\) nên \(\frac{{AD}}{4} = \frac{{DB}}{3} = \frac{{AD + DB}}{{4 + 3}} = \frac{{AB}}{7} = \frac{7}{7} = 1\) (tính chất của dãy tỉ số bằng nhau)
Suy ra \(AD = 4cm,DB = 3cm\)
Áp dụng hệ quả của định lí Thalès, ta có: \(\frac{{AD}}{{AB}} = \frac{{DE}}{{BC}}\)
Suy ra \(DE = \frac{{AD}}{{AB}}.BC = \frac{4}{7}.12 = \frac{{48}}{7}\)
d) Đúng
Vì DI // BM nên \(\frac{{AI}}{{AM}} = \frac{{DI}}{{BM}}\) (hệ quả của định lí Thalès)
Vì IE // CM nên \(\frac{{AI}}{{AM}} = \frac{{IE}}{{MC}}\) (hệ quả của định lí Thalès)
Do đó \(\frac{{DI}}{{BM}} = \frac{{IE}}{{MC}}\). Mà \(BM = MC\) nên \(DI = IE\).
Đáp án: SĐSĐ
Biểu đồ dưới đây cho biết doanh thu 12 tháng của một cửa hàng A.
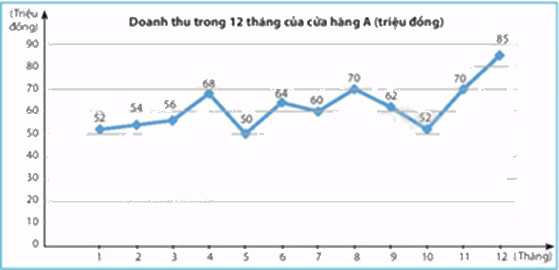
Tính độ chênh lệch giữa doanh thu cao nhất và doanh thu thấp nhất của cửa hàng trên. (đơn vị: triệu đồng)
Đáp án:
Đáp án:
Xác định doanh thu cao nhất, doanh thu thấp nhất.
Độ chênh lệch = doanh thu cao nhất – doanh thu thấp nhất.
Doanh thu cao nhất: 85 triệu đồng, doanh thu thấp nhất: 50 triệu đồng
Độ chênh lệch giữa doanh thu cao nhất và doanh thu thấp nhất của cửa hàng trên là: 85 – 50 = 35 (triệu đồng)
Đáp án: 35
Tỉ lệ số học sinh nam của lớp 8A là \(34\% \). Chọn ra ngẫu nhiên một học sinh trong lớp. Xác suất của biến cố “Học sinh được chọn ra là học sinh nữ” là (viết dưới dạng số thập phân).
Đáp án:
Đáp án:
Xác định tỉ lệ số học sinh nữ của lớp 8A.
Khi đó ta tính được xác suất của biến cố “Học sinh được chọn ra là học sinh nữ”.
Tỉ lệ số học sinh nữ của lớp 8A là: \(100\% - 34\% = 66\% \).
Xác suất của biến cố “Học sinh được chọn ra là học sinh nữ” là: \(66\% = \frac{{66}}{{100}} = 0,66\).
Đáp án: 0,66
Cho tam giác ABC có AB = 9 cm, điểm D thuộc cạnh AB sao AD = 6 cm. Kẻ DE song song với BC (E \( \in \) AC), kẻ EF song song với CD (F \( \in \) AB). Độ dài đoạn thẳng AF bằng bao nhiêu cm?
Đáp án:
Đáp án:
Sử dụng hệ quả của định lí Thalès để tính tỉ số \(\frac{{AF}}{{AD}}\) theo \(\frac{{DE}}{{BC}}\): Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
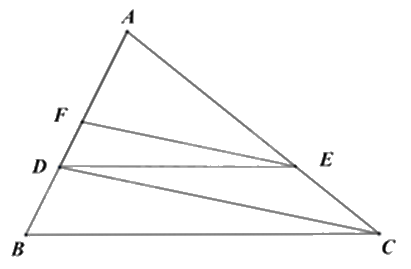
Vì DE // BC nên \(\frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{6}{9} = \frac{2}{3}\).
Vì EF // AD nên \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}} = \frac{2}{3}\)
Suy ra \(AF = \frac{2}{3}.AD = \frac{2}{3}.6 = 4\left( {cm} \right)\)
Đáp án: 4
Cho tam giác ABC có D, E lần lượt là trung điểm của các cạnh AB, AC và DE = 4cm.Biết đường cao AH = 6cm. Diện tích tam giác ABC là ...\(c{m^2}\).
Đáp án:
Đáp án:
Sử dụng tính chất đường trung bình trong tam giác và công thức tính diện tích tam giác.
- Đường trung bình của tam giác bằng một nửa cạnh thứ ba của tam giác đó.
- Diện tích tam giác = \(\frac{1}{2}\). chiều cao. đáy tương ứng.
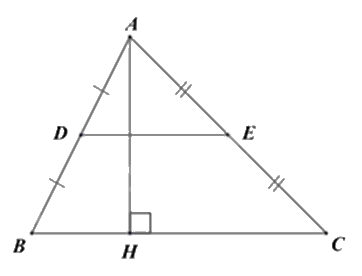
Xét tam giác ABC có D, E lần lượt là trung điểm của các cạnh AB, AC nên DE là đường trung bình của tam giác ABC. Do đó \(DE = \frac{1}{2}BC\).
Suy ra \(BC = 2.DE = 2.4 = 8\left( {cm} \right)\).
Diện tích tam giác ABC là: \({S_{\Delta ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Đáp án: 24
Biểu đồ dưới đây biểu diễn tốc độ tăng tổng sản phẩm trong nước (GDP) của nước ta 9 tháng đầu năm 2024 so với cùng kỳ năm trước.
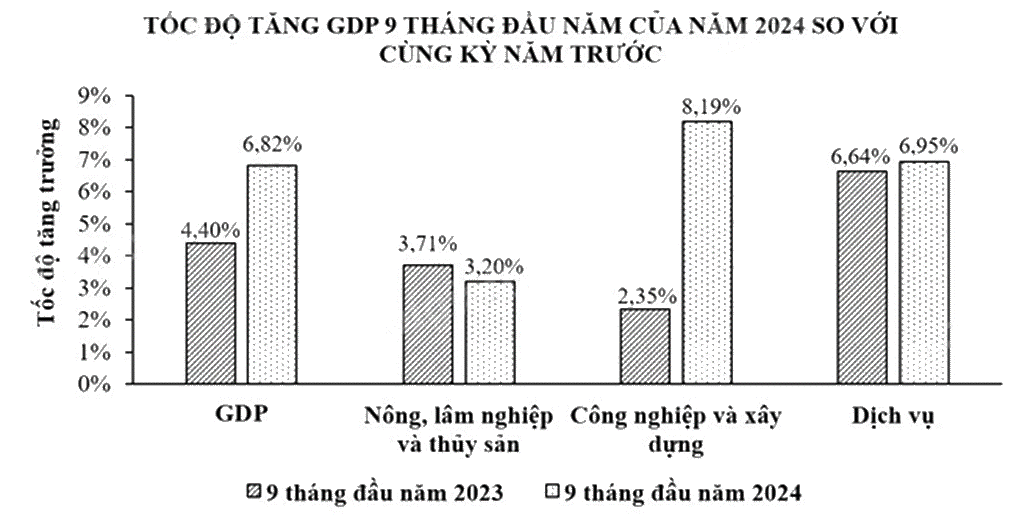
(Nguồn: Tổng cục thống kê)
a) Lập bảng thống kê tốc độ tăng GDP 9 tháng đầu năm 2024 của ba khu vực: Nông, lâm nghiệp và thủy sản; Công nghiệp và xây dựng; Dịch vụ.
b) Tốc độ tăng GDP 9 tháng đầu năm 2024 của khu vực Dịch vụ so với cùng kỳ năm trước tăng hay giảm bao nhiêu %?
c) Với ba khu vực trong bảng thống kê, khu vực nào có tốc độ tăng GDP 9 tháng đầu năm 2024 cao nhất so với cùng kỳ năm trước?
a) Từ biểu đồ cột kép lập bảng thống kê gồm: Khu vực, Tốc độ tăng GDP 9 tháng đầu năm 2024.
b) Quan sát cột GDP khu vực Dịch vụ để so sánh.
a) Bảng thống kê tốc độ tăng GDP 9 tháng đầu năm 2024 của ba khu vực:

b) GDP khu vực Dịch vụ 9 tháng đầu năm 2023 là 6,64%.
GDP khu vực Dịch vụ 9 tháng đầu năm 2024 là 6,95%.
Tốc độ tăng GDP 9 tháng đầu năm 2024 của khu vực Dịch vụ so với cùng kỳ năm trước tăng:
6,95% - 6,64% = 0,31%.
c) Tốc độ tăng GDP 9 tháng đầu năm 2024 của khu vực Nông, lâm nghiệp và thủy sản so với cùng kỳ năm trước tăng:
3,20% - 3,71% = -0,51%
Tốc độ tăng GDP 9 tháng đầu năm 2024 của khu vực Công nghiệp và xây dựng so với cùng kỳ năm trước tăng:
8,19% - 2,35% = 5,84%
Tốc độ tăng GDP 9 tháng đầu năm 2024 của khu vực Dịch vụ so với cùng kỳ năm trước tăng 0,31%.
Vậy trong ba khu vực, khu vực có tốc độ tăng GDP 9 tháng đầu năm 2024 cao nhất so với cùng kỳ năm trước là khu vực Công nghiệp và xây dựng, tăng 5,84%.
Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm của hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC. Chứng minh:
a) \(\Delta FBA = \Delta FCK\).
b) \(EF = \frac{{AB + CD}}{2}\).
a) Sử dụng tính chất hai đường thẳng song song suy ra \(\widehat {ABF} = \widehat {KCF}\).
Chứng minh \(\Delta FBA = \Delta FCK\) (g.c.g)
b) Từ \(\Delta FBA = \Delta FCK\) để chứng minh AB = CK, AF = FK .
Chứng minh EF là đường trung bình của tam giác ADK.
Kết hợp với AB = CK để được điều phải chứng minh.
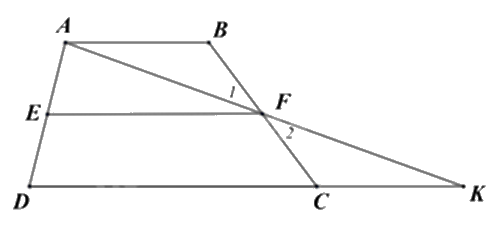
a) Vì AB // CD nên \(\widehat {ABF} = \widehat {KCF}\) (hai góc so le trong)
Xét \(\Delta FBA\) và \(\Delta FCK\) có:
\(\widehat {ABF} = \widehat {KCF}\) (cmt)
\(BF = FC\) (F là trung điểm của BC)
\(\widehat {{F_1}} = \widehat {{F_2}}\)
Suy ra \(\Delta FBA = \Delta FCK\) (g.c.g)
b) Vì \(\Delta FBA = \Delta FCK\) nên AB = CK, AF = FK (hai cặp cạnh tương ứng)
suy ra F là trung điểm của AK.
Xét tam giác ADK có E, F là trung điểm của AD, AK nên EF là đường trung bình của tam giác ADK, suy ra \(EF = \frac{{DK}}{2}\)
Mà DK = DC + CK = DC + AB (do AB = CK)
Do đó \(EF = \frac{{DC + AB}}{2}\).
Kỳ thi giữa học kỳ 2 Toán 8 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh. Đề thi giữa kì 2 Toán 8 Cánh diều - Đề số 10 là một bài kiểm tra toàn diện, bao gồm các kiến thức trọng tâm được giảng dạy trong giai đoạn học kỳ. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết để giúp học sinh ôn tập hiệu quả.
Đề thi giữa kì 2 Toán 8 Cánh diều - Đề số 10 thường bao gồm các phần sau:
Tỷ lệ điểm giữa phần trắc nghiệm và tự luận có thể khác nhau tùy theo quy định của từng trường. Tuy nhiên, phần tự luận thường chiếm trọng số lớn hơn, đòi hỏi học sinh phải nắm vững kiến thức và kỹ năng giải toán.
Trong đề thi giữa kì 2 Toán 8 Cánh diều - Đề số 10, học sinh có thể gặp các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải các bài tập trong đề thi, chúng ta sẽ cùng xem xét một số ví dụ cụ thể:
Giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 4 / 2
x = 2
Vậy nghiệm của phương trình là x = 2.
Giải:
(x2 - 4) / (x + 2) = (x - 2)(x + 2) / (x + 2)
= x - 2 (với x ≠ -2)
Vậy biểu thức được rút gọn là x - 2.
Để đạt kết quả tốt nhất trong kỳ thi giữa học kỳ 2 Toán 8, học sinh nên:
Đề thi giữa kì 2 Toán 8 Cánh diều - Đề số 10 là một cơ hội tốt để học sinh kiểm tra và củng cố kiến thức đã học. Bằng cách ôn tập kỹ lưỡng và luyện tập thường xuyên, các em có thể tự tin đối mặt với kỳ thi và đạt được kết quả tốt nhất. Chúc các em thành công!