Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 8 - Đề số 3 - Cánh diều, một tài liệu ôn tập vô cùng quan trọng dành cho học sinh lớp 8. Đề thi này được biên soạn theo chương trình sách giáo khoa Cánh diều, bao gồm các dạng bài tập thường gặp trong đề thi thực tế.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
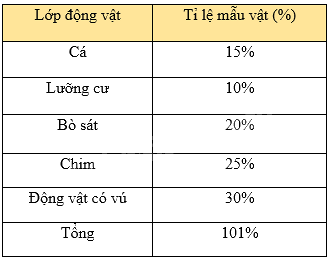
Cho bảng thống kê tỉ lệ các loại mẫu vật trong bảo tàng sinh vật của môi trường đại học về những lớp động vật có xương sống: Cá, Lưỡng cư, Bò sát, Chim, Động vật có vú.
Giá trị chưa hợp lí trong bảng dữ liệu là:
Trong cuộc khảo sát tìm hiểu về cách học của học sinh khối 8 được kết quả như sau:
Có 50% học sinh học qua đọc, viết.
Có 35% học sinh học qua nghe
Có 10% học qua vận động
Có 5% học sinh học qua quan sát.
Khẳng định nào sau đây là đúng?
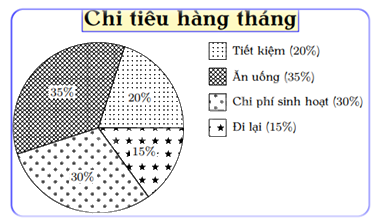
Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm kế hoạch chi tiêu hàng tháng của gia đình bác An. Số tiền chi tiêu hàng tháng của gia đình bác An dành cho ăn uống gấp bao nhiêu lần số tiền dành cho tiết kiệm?
Một túi đựng các quả cầu giống hệt nhau, chỉ khác màu, trong đó có 26 quả màu đỏ, 62 quả màu tím, 8 quả màu vàng, 9 quả màu trắng. Lấy ngẫu nhiên 1 quả trong túi. Xác suất để lấy được quả cầu màu tím là:
Gieo một con xúc xắc cân đối và đồng chất. Xác suất của biến cố “Gieo được mặt có số chấm chẵn” là
Tỉ lệ học sinh bị cận thị ở một trường trung học cơ sở là 18%. Gặp ngẫu nhiên một học sinh ở trường, xác suất học sinh đó bị cận thị là:
M, N là trung điểm các cạnh AB, AC của tam giác ABC. Khi MN = 8cm thì:
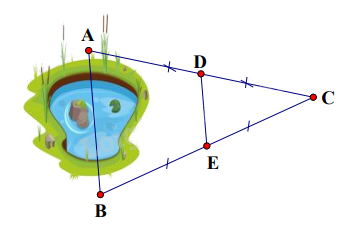
Hai điểm A và B ở hai bờ của một hồ nước (hình vẽ) có độ dài đoạn thẳng DE bằng 100 mét. Hãy xác định khoảng cách AB.
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
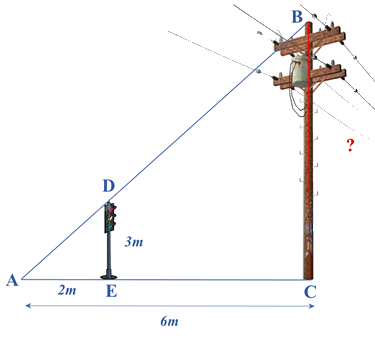
Bóng của một cột điện trên mặt đất dài 6m. Cùng lúc đó, một cột đèn giao thông cao 3m có bóng dài 2m. Tính chiều cao của cột điện.
Cho hình vẽ, biết MN // BC. Khẳng định nào dưới đây là sai?
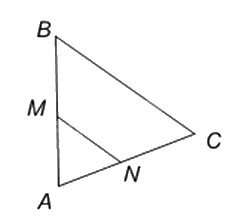
Cho hình vẽ sau, biết DT là tia phân giác của \(\widehat {EDF}\). Tỉ số \(\frac{x}{y}\) bằng:
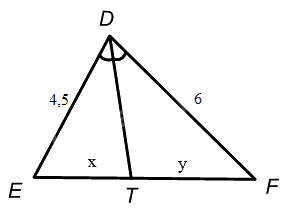
Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 12; 18; 22; 27; 69; 96; 99. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa . Quay ngẫu nhiên một lần, ghi kết quả xảy ra đối với số ở hình quạt . Trong 32 lần quay số liên tiếp, có 6 lần mũi tên chỉ vào số 22, có 2 lần mũi tên chỉ vào số 18, có 10 lần mũi tên chỉ vào số 96.
a) Tính xác suất thực nghiệm của biến cố “ Mũi tên chỉ vào số 22”.
b) Tính xác suất thực nghiệm của biến cố “ Mũi tên chỉ vào số 18”.
c) Tính xác suất thực nghiệm của biến cố “ Mũi tên chỉ vào số 96”.
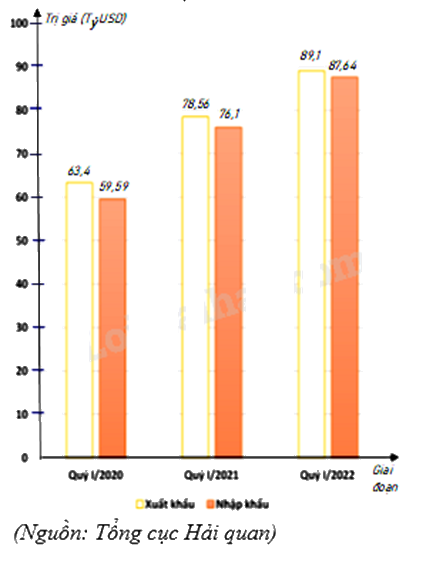
Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022.
a) Lập bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022: đơn vị (tỷ USD) theo mẫu sau:
Giai đoạn | Quý I/2020 | Quý I/2021 | Quý I/2022 |
Xuất khẩu | ? | ? | ? |
Nhập khẩu | ? | ? | ? |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
c) Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
d) Trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 giảm bao nhiêu phần trăm so với quý I năm 2021 (làm tròn kết quả đến hàng phần mười) ?
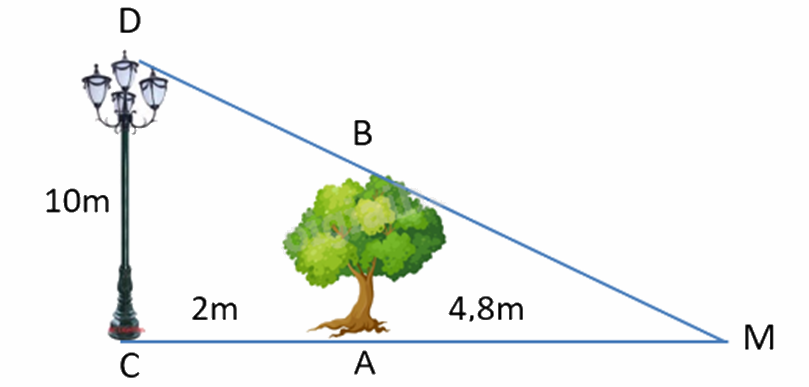
Một cột đèn cao 10m chiếu sáng một cây xanh như hình dưới. Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét)
1. Tính \(x\) trong hình và làm tròn kết quả đến hàng phần mười.
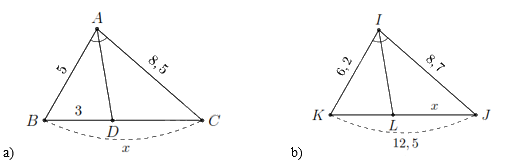
2. Hình thang ABCD (AB // CD) có DC = 2AB. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh các tứ giác ABPD, MNPQ là hình bình hành.
b) Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi.
c) Gọi E là giao điểm của BD và AP. Chứng minh ba điểm Q, N, E thẳng hàng.
Chứng minh rằng nếu a, b, c khác nhau đôi một thì:
\(\frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}} = \frac{2}{{a - b}} + \frac{2}{{b - c}} + \frac{2}{{c - a}}\).
Cho bảng thống kê tỉ lệ các loại mẫu vật trong bảo tàng sinh vật của môi trường đại học về những lớp động vật có xương sống: Cá, Lưỡng cư, Bò sát, Chim, Động vật có vú.
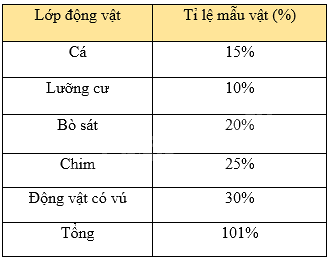
Giá trị chưa hợp lí trong bảng dữ liệu là:
Đáp án : B
Quan sát bảng thống kê để xác định.
Trong bảng thống kê trên, ta thấy tổng tỉ lệ mẫu vật bằng 15% + 10% + 20% + 25% + 30% = 100% nên dữ liệu về tổng tỉ lệ mẫu vật chưa chính xác. Vậy dữ liệu tỉ lệ mẫu vật chưa hợp lí.
Trong cuộc khảo sát tìm hiểu về cách học của học sinh khối 8 được kết quả như sau:
Có 50% học sinh học qua đọc, viết.
Có 35% học sinh học qua nghe
Có 10% học qua vận động
Có 5% học sinh học qua quan sát.
Khẳng định nào sau đây là đúng?
Đáp án : D
Dựa vào kiến thức về dữ liệu định tính, dữ liệu định lượng.
Trong kết quả trên:
+ Các hình thức học: đọc viết; nghe; vận động; quan sát là dữ liệu định tính.
+ Số lượng học sinh có cách học qua đọc, viết; nghe; vận động; quan sát lần lượt là: 50%, 30%, 10%, 5% là dữ liệu định lượng.
Do đó kết quả trên gồm cả dữ liệu định tính và dữ liệu định lượng.
Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm kế hoạch chi tiêu hàng tháng của gia đình bác An. Số tiền chi tiêu hàng tháng của gia đình bác An dành cho ăn uống gấp bao nhiêu lần số tiền dành cho tiết kiệm?
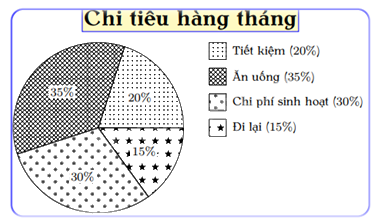
Đáp án : D
Quan sát biểu đồ, chỉ ra số phần trăm gia đình bác An dành cho ăn uống, số phần trăm dành cho tiết kiệm.
Gia đình bác An dành 35% số tiền cho ăn uống; 20% số tiền cho tiết kiệm
\( \Rightarrow \) Số tiền chi tiêu hàng tháng của gia đình bác An dành cho ăn uống gấp số tiền dành cho tiết kiệm là:
\(\frac{{35\% }}{{20\% }} = \frac{{35}}{{20}} = 1,75\) (lần)
Một túi đựng các quả cầu giống hệt nhau, chỉ khác màu, trong đó có 26 quả màu đỏ, 62 quả màu tím, 8 quả màu vàng, 9 quả màu trắng. Lấy ngẫu nhiên 1 quả trong túi. Xác suất để lấy được quả cầu màu tím là:
Đáp án : A
Tính số quả cầu.
Xác suất để lấy được quả cầu màu tím bằng tỉ số giữa số quả cầu màu tím với tổng số quả cầu.
Tổng số quả cầu là: 26 + 62 + 8 + 9 = 105 (quả)
Xác suất để lấy được quả cầu màu tím là: \(\frac{{62}}{{105}}\).
Gieo một con xúc xắc cân đối và đồng chất. Xác suất của biến cố “Gieo được mặt có số chấm chẵn” là
Đáp án : A
Tính các kết quả thuận lợi cho biến cố “Gieo được mặt có số chấm chẵn”.
Tính số kết quả có thể.
Xác suất của biến cố “Gieo được mặt có số chấm chẵn” bằng tỉ số giữa số kết quả thuận lợi của biến cố với số kết quả có thể.
Có 3 kết quả thuận lợi cho biến cố “Gieo được mặt có số chấm chẵn”, đó là: 2; 4; 6.
Xác suất của biến cố “Gieo được mặt có số chấm chẵn” là: \(\frac{3}{6} = \frac{1}{2}\).
Tỉ lệ học sinh bị cận thị ở một trường trung học cơ sở là 18%. Gặp ngẫu nhiên một học sinh ở trường, xác suất học sinh đó bị cận thị là:
Đáp án : A
Xác suất bằng tỉ lệ học sinh bị cận thị của trường đó.
Xác suất gặp ngẫu nhiện một học sinh ở trường mà học sinh đó bị cận thị là: \(18\% = 0,18\).
M, N là trung điểm các cạnh AB, AC của tam giác ABC. Khi MN = 8cm thì:
Đáp án : C
Sử dụng tính chất đường trung bình.
Ta có M, N là trung điểm các cạnh AB, AC của tam giác ABC nên MN là đường trung bình của tam giác ABC, khi đó MN = \(\frac{1}{2}\)BC.
Mà MN = 8cm nên BC = 8.2 = 16 cm.
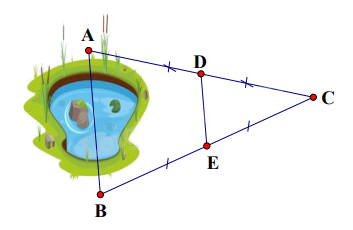
Hai điểm A và B ở hai bờ của một hồ nước (hình vẽ) có độ dài đoạn thẳng DE bằng 100 mét. Hãy xác định khoảng cách AB.
Đáp án : A
Sử dụng tính chất của đường trung bình trong tam giác.
Theo hình vẽ, ta thấy AD = DC; BE = EC nên D là trung điểm của AC và E là trung điểm của BC. Khi đó DE là đường trung bình của tam giác ABC => DE = \(\frac{1}{2}\)AB.
Mà DE = 100m => AB = 2.100 = 200(m).
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
Đáp án : B
Sử dụng định lí Thales đảo để chứng minh.
Tam giác ABC cân tại A nên AB = AC.
Vì BM = CN; AB = AC nên AB – BM = AC – CN hay AM = AN
Suy ra \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) => MN // BC (định lí Thales đảo).
Khi đó BMNC là hình thang. Mà BM = CN nên BMNC là hình thang cân.
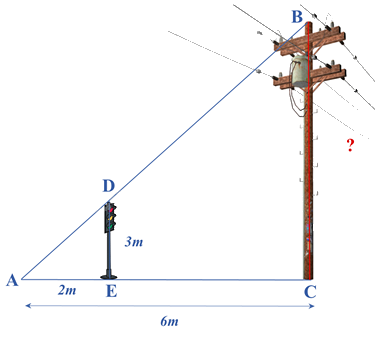
Bóng của một cột điện trên mặt đất dài 6m. Cùng lúc đó, một cột đèn giao thông cao 3m có bóng dài 2m. Tính chiều cao của cột điện.
Đáp án : C
Áp dụng hệ quả của định lí Thales trong tam giác.
Vì cột đèn giao thông và cột điện cùng vuông góc với mặt đất nên song song với nhau.
\( \Rightarrow DE//BC\).
Áp dụng hệ quả của định lí Thales trong tam giác, ta có:
\(\begin{array}{l}\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\\\frac{2}{6} = \frac{3}{{BC}} \Rightarrow BC = 3:\frac{2}{6} = 9\left( m \right)\end{array}\)
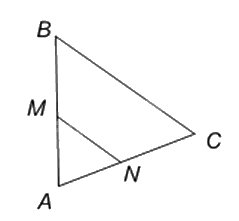
Cho hình vẽ, biết MN // BC. Khẳng định nào dưới đây là sai?
Đáp án : A
Áp dụng định lí Thales trong tam giác.
Xét tam giác ABC có MN // BC \( \Rightarrow \frac{{AM}}{{BM}} = \frac{{AN}}{{NC}}\)
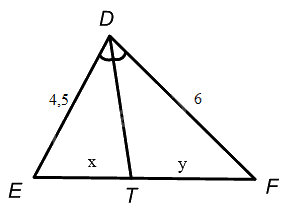
Cho hình vẽ sau, biết DT là tia phân giác của \(\widehat {EDF}\). Tỉ số \(\frac{x}{y}\) bằng:
Đáp án : B
Dựa vào tính chất đường phân giác trong tam giác.
Ta có DT là tia phân giác của \(\widehat {EDF}\) nên ta có:
\(\frac{{DE}}{{ET}} = \frac{{DF}}{{TF}} \Rightarrow \frac{x}{y} = \frac{{ET}}{{TF}} = \frac{{DE}}{{DF}} = \frac{{4,5}}{6} = \frac{3}{4}\) (theo tính chất của đường phân giác)
Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 12; 18; 22; 27; 69; 96; 99. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa . Quay ngẫu nhiên một lần, ghi kết quả xảy ra đối với số ở hình quạt . Trong 32 lần quay số liên tiếp, có 6 lần mũi tên chỉ vào số 22, có 2 lần mũi tên chỉ vào số 18, có 10 lần mũi tên chỉ vào số 96.
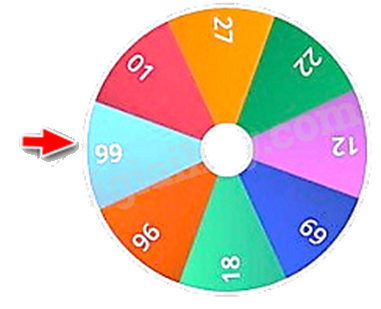
a) Tính xác suất thực nghiệm của biến cố “ Mũi tên chỉ vào số 22”.
b) Tính xác suất thực nghiệm của biến cố “ Mũi tên chỉ vào số 18”.
c) Tính xác suất thực nghiệm của biến cố “ Mũi tên chỉ vào số 96”.
Xác suất thực nghiệm của biến cố bằng tỉ số giữa số lần mũi tên chỉ vào số đó với tổng số lần quay.
a) Số lần mũi tên chỉ vào số 22 là 2 lần.
Xác suất thực nghiệm của biến cố “ Mũi tên chỉ vào số 22” là: \(\frac{6}{{32}} = \frac{3}{{16}}\).
b) Số lần mũi tên chỉ vào số 18 là 6 lần.
Xác suất thực nghiệm của biến cố “ Mũi tên chỉ vào số 18” là: \(\frac{2}{{32}} = \frac{1}{{16}}\).
c) Số lần mũi tên chỉ vào số 96 là 10 lần.
Xác suất thực nghiệm của biến cố “ Mũi tên chỉ vào số 96” là: \(\frac{{10}}{{32}} = \frac{5}{{16}}\).
Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022.
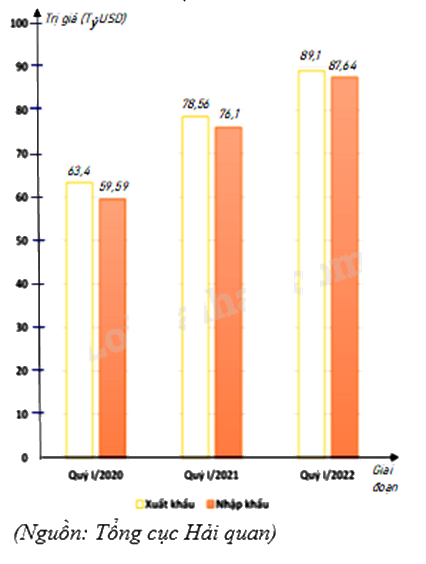
a) Lập bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022: đơn vị (tỷ USD) theo mẫu sau:
Giai đoạn | Quý I/2020 | Quý I/2021 | Quý I/2022 |
Xuất khẩu | ? | ? | ? |
Nhập khẩu | ? | ? | ? |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
c) Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
d) Trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 giảm bao nhiêu phần trăm so với quý I năm 2021 (làm tròn kết quả đến hàng phần mười) ?
Dựa vào bảng dữ liệu để trả lời.
a) Bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022: đơn vị (tỷ USD)
Giai đoạn | Quý I/2020 | Quý I/2021 | Quý I/2022 |
Xuất khẩu | 63,4 | 78,56 | 89,1 |
Nhập khẩu | 59,59 | 76,1 | 87,64 |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là:
63,4 + 78,56 + 89,1 = 231,06 (tỷ USD)
c) Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là
59,59 + 76,1 + 87,64 = 223,33 (tỷ USD)
d) Tỉ số phần trăm trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 và quý I năm 2021 là: \(\frac{{63,4}}{{78,56}}.100\% = 80,7\% \)
Trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 giảm 100 % - 80,7 % = 19,3 % so với quý I năm 2021.
Một cột đèn cao 10m chiếu sáng một cây xanh như hình dưới. Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét)
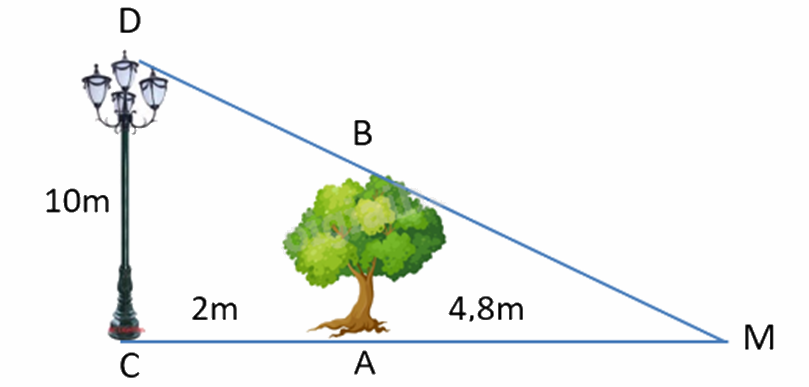
Áp dụng hệ quả của định lí Thales để tính chiều cao cây xanh.
Khoảng cách từ điểm C đến điểm M là: 2 + 4,8 = 6,8 (m).
Vì cột đèn và cái cây đều vuông góc với mặt đất nên ta có AB // CD.
Xét tam giác CMD có AB // CD nên:
\(\begin{array}{l}\frac{{AB}}{{AM}} = \frac{{CD}}{{CM}}\\\frac{{AB}}{{4,8}} = \frac{{10}}{{6,8}} \Rightarrow AB = 4,8.\frac{{10}}{{6,8}} = \frac{{120}}{{17}} \approx 7\left( m \right)\end{array}\)
Vậy chiều cao của cây xanh là khoảng 7m.
1. Tính \(x\) trong hình và làm tròn kết quả đến hàng phần mười.
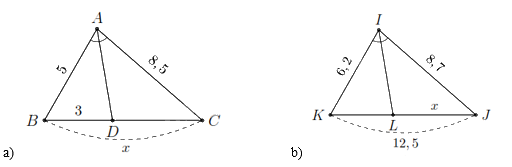
2. Hình thang ABCD (AB // CD) có DC = 2AB. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh các tứ giác ABPD, MNPQ là hình bình hành.
b) Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi.
c) Gọi E là giao điểm của BD và AP. Chứng minh ba điểm Q, N, E thẳng hàng.
1. Dựa vào tính chất đường phân giác, sử dụng tỉ số bằng nhau để tính.
2.
a) Dựa vào dấu hiệu nhận biết hình bình hành và tính chất đường trung bình để chứng minh.
b) Dựa vào dấu hiệu nhận biết hình thoi và tính chất đường trung bình.
c) Sử dụng tính chất đường trung bình để chứng minh EQ // AB và EN // AB suy ra Q, N, E thẳng hàng.
1.
a)
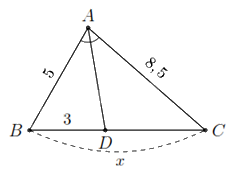
Do \(AD\) là đường phân giác trong của góc \(A\) nên ta có
\(\frac{{DC}}{{DB}} = \frac{{AC}}{{AB}} \Rightarrow DC = \frac{{AC}}{{AB}} \cdot DB.\)
Thay số ta có \(DC = \frac{{8,5}}{5} \cdot 3 = 5,1\). Khi đó \(x = DB + DC = 3 + 5,1 = 8,1\).
b)
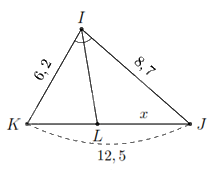
Với \(KL = 12,5 - x\) và do \(IL\) là đường phân giác trong của góc \(I\) nên theo tính chất đường phân giác ta có
Theo tính chất đường phân giác ta có
\(\frac{{KL}}{{LJ}} = \frac{{IK}}{{IJ}} \Rightarrow \frac{{12,5 - x}}{x} = \frac{{6,2}}{{8,7}} \Leftrightarrow x = \frac{{2175}}{{298}} \approx 7,3\).
2.
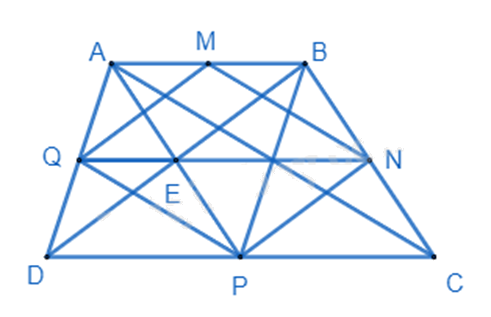
a) Ta có: \(DP = \frac{1}{2}DC = AB\); \(AB//CD \Rightarrow AB//DP\) nên ABPD là hình bình hành.
Vẽ AC, ta có MN là đường trung bình \(\Delta ABC \Rightarrow MN = \frac{1}{2}AC;MN//AC\).
Chứng minh tương tự \( \Rightarrow PQ = \frac{1}{2}AC;PQ//AC\).
\( \Rightarrow MN = PQ;PQ//AC\) nên MNPQ là hình bình hành.
b)
Tương tự như đường chéo AC, vẽ BD, ta cũng chứng minh được MQ và NP là đường trung bình của tam giác ABD và BCD nên \(MQ = NP = \frac{1}{2}BD;MQ//NP//BD\).
MNPQ là hình thoi khi MN = MQ mà \(MN = \frac{1}{2}AC;MQ = \frac{1}{2}BD\) (tính chất đường trung bình)
\( \Rightarrow AC = BD\). Khi đó ABCD là hình thang cân.
c) Vì ABPD là hình bình hành nên E là trung điểm của AP.
Xét tam giác ABD có QE là đường trung bình của tam giác ABD nên QE // AB (1)
Xét tam giác DBC có EN là đường trung bình của tam giác DBC nên EN // DC mà DC // AB nên EN // AB (2)
Từ (1) và (2) suy ra từ E kẻ được EQ // AB và EN // AB nên Q, E, N thẳng hàng
Chứng minh rằng nếu a, b, c khác nhau đôi một thì:
\(\frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}} = \frac{2}{{a - b}} + \frac{2}{{b - c}} + \frac{2}{{c - a}}\).
Áp dụng đẳng thức \(\frac{1}{a} - \frac{1}{b} = \frac{{b - a}}{{ab}}\)
Xét phân thức \(\frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}}\)\( = \frac{{a - c - a + b}}{{\left( {a - b} \right)\left( {a - c} \right)}}\)\( = \frac{{a - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} - \frac{{a - b}}{{\left( {a - b} \right)\left( {a - c} \right)}}\)\( = \frac{1}{{a - b}} - \frac{1}{{a - c}}\).
Tương tự ta có: \(\frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} = \frac{1}{{b - c}} - \frac{1}{{b - a}}\)
\(\frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}} = \frac{1}{{c - a}} - \frac{1}{{c - b}}\)
\( \Rightarrow \frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}}\)
\( = \frac{1}{{a - b}} - \frac{1}{{a - c}} + \frac{1}{{b - c}} - \frac{1}{{b - a}} + \frac{1}{{c - a}} - \frac{1}{{c - b}}\)
\( = \frac{1}{{a - b}} + \frac{1}{{c - a}} + \frac{1}{{b - c}} + \frac{1}{{a - b}} + \frac{1}{{c - a}} + \frac{1}{{b - c}}\)
\( = \frac{2}{{a - b}} + \frac{2}{{b - c}} + \frac{2}{{c - a}}\) (đpcm).
Đề thi giữa kì 2 Toán 8 - Đề số 3 - Cánh diều là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức của học sinh sau nửa học kỳ 2. Đề thi bao gồm các chủ đề chính như biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức, hệ phương trình bậc nhất hai ẩn, và các ứng dụng thực tế của đại số.
Thông thường, đề thi giữa kì 2 Toán 8 - Cánh diều có cấu trúc gồm hai phần chính:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 2 Toán 8 - Cánh diều:
Để đạt kết quả tốt trong kỳ thi giữa kì 2 Toán 8 - Cánh diều, học sinh cần:
Bài 1: Giải phương trình 2x + 3 = 7
Lời giải:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Hãy dành thời gian ôn tập kỹ lưỡng và làm quen với các dạng bài tập thường gặp trong đề thi giữa kì 2 Toán 8 - Cánh diều. Chúc các em học sinh đạt kết quả tốt nhất!