Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 8 Cánh diều - Đề số 6, một công cụ ôn luyện hiệu quả giúp học sinh nắm vững kiến thức và tự tin bước vào kỳ thi. Đề thi được biên soạn theo chương trình học mới, bám sát nội dung sách giáo khoa và có đáp án chi tiết đi kèm.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết các bài toán khác nhau, từ đó nâng cao năng lực toán học.
Biểu thức thích hợp của đẳng thức \({x^2} + ... + 4{y^2} = {\left( {x + 2y} \right)^2}\) là:
\(xy\).
\(4xy\).
\(2xy\).
\( - 4xy\).
Kết quả của phép tính \({72^2} + {22^2} - 44.72\) là:
784.
250.
2500.
8836.
Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng 8cm và độ dài trung đoạn bằng 15cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
\(960c{m^2}\).
\(240c{m^2}\).
\(480c{m^2}\).
\(150c{m^2}\).
Tam giác có độ dài ba cạnh trong trường hợp nào sau đây là tam giác vuông?
10cm, 6cm, 9cm.
3cm, 4cm, 6cm.
11cm, 6cm, 8cm.
12cm, 35cm, 37cm.
Cho mặt phẳng tọa độ Oxy như hình vẽ. Tọa độ điểm M là:
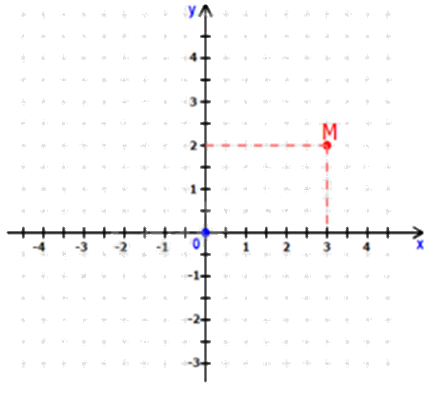
M(3;2).
M(2;3).
M(3;0).
M(0;2).
Cho hàm số \(y = f\left( x \right) = \frac{1}{3}x - 1\). Giá trị của \(f\left( { - 3} \right)\) là:
0.
-2.
-4.
1.
Hình chóp tam giác đều có:
4 mặt, 5 cạnh.
3 mặt, 6 cạnh.
6 mặt, 6 cạnh.
4 mặt, 6 cạnh.
Xác định các hệ số của \(x\), hệ số tự do của hàm số bậc nhất \(y = - \frac{1}{2}x + 7\).
Hệ số của \(x\) là \( - \frac{1}{2}\). Hệ số tự do là \( - 7\).
Hệ số của \(x\) là \( - \frac{1}{2}\). Hệ số tự do là \(7\).
Hệ số của \(x\) là \(\frac{1}{2}\). Hệ số tự do là \( - 7\).
Hệ số của \(x\) là \(1\). Hệ số tự do là \( - 7\).
Cho hình chóp tam giác đều có diện tích đáy là \(18c{m^2}\) và chiều cao là \(5cm\). Thể tích của hình chóp tam giác đều là:
\(23c{m^3}\).
\(45c{m^3}\).
\(30c{m^3}\).
\(90c{m^3}\).
Kết quả của phép tính \(\left( {8{x^9}{y^2} - 6{x^6}{y^3} + {x^3}{y^4}} \right):2{x^3}{y^2}\) là:
\(4{x^3} - 3{x^2}y + 2{y^2}\).
\(4{x^6}y - 3{x^3} + 2{y^2}\).
\(4{x^6} - 3{x^3}y + \frac{1}{2}{y^2}\).
\(4{x^6} - 3{x^3}y + 1\).
Mẹ Lan đưa cho Lan 210 000 đồng lên siêu thị gần nhà mua xoài. Biết rằng giá 1 kg xoài là 50 000 đồng. Hãy tính số tiền \(y\) (đồng) còn lại khi mua \(x\) kg xoài và cho biết \(y\) có phải là hàm số của \(x\) hay không?
\(y = 210\,000 - 50\,000x\); \(y\) là hàm số của \(x\).
\(y = 210\,000 - 50\,000x\); \(y\) không phải là hàm số của \(x\).
\(y = 210\,000 + 50\,000x\); \(y\) là hàm số của \(x\).
\(y = 210\,000 + 50\,000x\); \(y\) không phải là hàm số của \(x\).
Điền cụm từ thích hợp vào chỗ trống (…)
Hình thang có … là hình thang cân.
hai cạnh bên bằng nhau.
hai đường chéo bằng nhau.
hai cạnh bên song song.
hai đường chéo vuông góc với nhau.
Phân tích đa thức thành nhân tử:
a) \({x^2} - 9\)
b) \({x^2} - 4x + 4 - {y^2}\)
Cho biểu thức \(A = \frac{{2x - 3}}{{x - 1}}\) và \(B = \frac{x}{{x - 1}} + \frac{3}{{x + 1}} - \frac{{6x - 4}}{{{x^2} - 1}}\) (với \(x \ne \pm 1\))
a) Tính giá trị của A khi \(x = 2\).
b) Chứng minh rằng biểu thức \(B = \frac{{x - 1}}{{x + 1}}\).
c) Tìm các số nguyên dương \(x\) để biểu thức \(P = A.B\) nhận giá trị là số nguyên.
Một công nhân theo kế hoạch cần phải làm 120 sản phẩm trong một số giờ dự kiến, với số sản phẩm dự kiến làm trong một giờ là \(x\) sản phẩm. Sau khi làm được 2 giờ với năng suất dự kiến, công nhân đó đã tăng năng suất được 3 sản phẩm mỗi giờ, vì vậy công nhân đó đã hoàn thành kế hoạch sớm hơn thời gian dự kiến.
a) Hãy viết biểu thức biểu thị thời gian công nhân đó dự kiến hoàn thành kế hoạch.
b) Hãy viết biểu thức biểu thị thời gian công nhân đó hoàn thành kế hoạch sớm hơn thời gian dự kiến.
Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của BC và AC. Trên tia đối của tia MN lấy điểm D sao cho MD = MN.
a) Chứng minh tứ giác BDCN là hình bình hành.
b) Chứng minh AD = BN.
c) Cho biết độ dài AM = 5cm, AC = 8cm. Tính diện tích tam giác vuông ABC?
Cho các số \(x,y\) thỏa mãn đẳng thức \(\frac{1}{2}{x^2} + 2{y^2} - x + 2y + 1 = 0\). Tính giá trị của biểu thức \(M = {\left( {x + 2y} \right)^{2022}} + {\left( {x - 2} \right)^{2023}} + {\left( {y + \frac{3}{2}} \right)^{2024}}\).
Biểu thức thích hợp của đẳng thức \({x^2} + ... + 4{y^2} = {\left( {x + 2y} \right)^2}\) là:
\(xy\).
\(4xy\).
\(2xy\).
\( - 4xy\).
Đáp án : B
Sử dụng hằng đẳng thức bình phương của một tổng: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
Ta có: \({\left( {x + 2y} \right)^2} = {x^2} + 2.x.2y + 4{y^2} = {x^2} + 4xy + 4{y^2}\) nên biểu thức còn thiếu là \(4xy\).
Đáp án B
Kết quả của phép tính \({72^2} + {22^2} - 44.72\) là:
784.
250.
2500.
8836.
Đáp án : C
Sử dụng hằng đẳng thức bình phương của một hiệu: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Ta có:
\(\begin{array}{l}{72^2} + {22^2} - 44.72\\ = {72^2} - 2.22.72 + {22^2}\\ = {\left( {72 - 22} \right)^2}\\ = {50^2} = 2500\end{array}\)
Đáp án C
Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng 8cm và độ dài trung đoạn bằng 15cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
\(960c{m^2}\).
\(240c{m^2}\).
\(480c{m^2}\).
\(150c{m^2}\).
Đáp án : B
Diện tích xung quanh của hình chóp tứ giác đều bằng nửa chu vi đáy nhân chiều cao.
Diện tích xung quanh của hình chóp tứ giác đều đó là:
\({S_{xq}} = \frac{1}{2}.\left( {8.4} \right).15 = 240\left( {c{m^2}} \right)\)
Đáp án B
Tam giác có độ dài ba cạnh trong trường hợp nào sau đây là tam giác vuông?
10cm, 6cm, 9cm.
3cm, 4cm, 6cm.
11cm, 6cm, 8cm.
12cm, 35cm, 37cm.
Đáp án : D
Áp dụng định lí Pythagore đảo: nếu bình phương một cạnh bằng tổng bình phương hai cạnh còn lại trong tam giác thì tam giác là tam giác vuông.
\({9^2} + {6^2} = 81 + 36 = 117 \ne 100 = {10^2}\) nên 10cm, 6cm, 9cm không phải độ dài ba cạnh của một tam giác vuông.
\({3^2} + {4^2} = 9 + 16 = 25 \ne 36 = {6^2}\) nên 3 cm, 4 cm, 6 cm không phải độ dài ba cạnh của một tam giác vuông.
\({6^2} + {8^2} = 36 + 64 = 100 \ne 121 = {11^2}\) nên 11cm, 6cm, 8cm không phải độ dài ba cạnh của một tam giác vuông.
\({12^2} + {35^2} = 144 + 1225 = 1369 = {37^2}\) nên 12cm, 35cm, 37cm là độ dài ba cạnh của một tam giác vuông.
Đáp án D
Cho mặt phẳng tọa độ Oxy như hình vẽ. Tọa độ điểm M là:
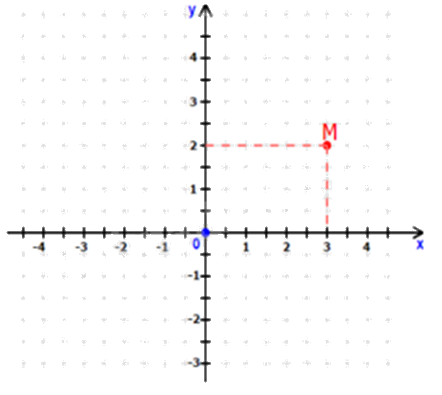
M(3;2).
M(2;3).
M(3;0).
M(0;2).
Đáp án : A
Quan sát mặt phẳng tọa độ, xác định tọa độ điểm \(M\left( {{x_M};{y_M}} \right)\).
Tọa độ điểm M trên mặt phẳng tọa độ là \(M\left( {3;2} \right)\).
Đáp án A
Cho hàm số \(y = f\left( x \right) = \frac{1}{3}x - 1\). Giá trị của \(f\left( { - 3} \right)\) là:
0.
-2.
-4.
1.
Đáp án : B
Thay \(x = - 3\) vào hàm số \(y = f\left( x \right)\) để tính giá trị.
Giá trị của \(f\left( { - 3} \right)\) là:
\(y = f\left( { - 3} \right) = \frac{1}{3}.\left( { - 3} \right) - 1 = - 1 - 1 = - 2\).
Đáp án B
Hình chóp tam giác đều có:
4 mặt, 5 cạnh.
3 mặt, 6 cạnh.
6 mặt, 6 cạnh.
4 mặt, 6 cạnh.
Đáp án : D
Dựa vào đặc điểm của hình chóp tam giác đều.
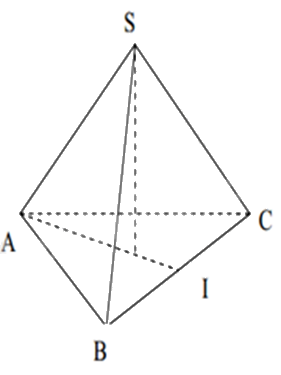
Hình chóp tam giác đều có 4 mặt (3 mặt bên, 1 mặt đáy) và 6 cạnh.
Đáp án D
Xác định các hệ số của \(x\), hệ số tự do của hàm số bậc nhất \(y = - \frac{1}{2}x + 7\).
Hệ số của \(x\) là \( - \frac{1}{2}\). Hệ số tự do là \( - 7\).
Hệ số của \(x\) là \( - \frac{1}{2}\). Hệ số tự do là \(7\).
Hệ số của \(x\) là \(\frac{1}{2}\). Hệ số tự do là \( - 7\).
Hệ số của \(x\) là \(1\). Hệ số tự do là \( - 7\).
Đáp án : B
Hàm số bậc nhất \(y = ax + b\) có hệ số của \(x\) là \(a\) và hệ số tự do là \(b\).
Hàm số bậc nhất \(y = - \frac{1}{2}x + 7\) có hệ số của \(x\) là \( - \frac{1}{2}\) và hệ số tự do là \(7\).
Đáp án B
Cho hình chóp tam giác đều có diện tích đáy là \(18c{m^2}\) và chiều cao là \(5cm\). Thể tích của hình chóp tam giác đều là:
\(23c{m^3}\).
\(45c{m^3}\).
\(30c{m^3}\).
\(90c{m^3}\).
Đáp án : C
Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) diện tích đáy nhân chiều cao: V = \(\frac{1}{3}\)Sđáy.h.
Thể tích của hình chóp tam giác đều là:
\(V = \frac{1}{3}.18.5 = 30\left( {c{m^3}} \right)\).
Đáp án C
Kết quả của phép tính \(\left( {8{x^9}{y^2} - 6{x^6}{y^3} + {x^3}{y^4}} \right):2{x^3}{y^2}\) là:
\(4{x^3} - 3{x^2}y + 2{y^2}\).
\(4{x^6}y - 3{x^3} + 2{y^2}\).
\(4{x^6} - 3{x^3}y + \frac{1}{2}{y^2}\).
\(4{x^6} - 3{x^3}y + 1\).
Đáp án : C
Áp dụng quy tắc chia đa thức cho đơn thức: ta chia lần lượt các hạng tử của đa thức cho đơn thức.
Ta có:
\(\begin{array}{l}\left( {8{x^9}{y^2} - 6{x^6}{y^3} + {x^3}{y^4}} \right):2{x^3}{y^2}\\ = 8{x^9}{y^2}:2{x^3}{y^2} - 6{x^6}{y^3}:2{x^3}{y^2} + {x^3}{y^4}:2{x^3}{y^2}\\ = 4{x^6} - 3{x^3}y + \frac{1}{2}{y^2}\end{array}\)
Đáp án C
Mẹ Lan đưa cho Lan 210 000 đồng lên siêu thị gần nhà mua xoài. Biết rằng giá 1 kg xoài là 50 000 đồng. Hãy tính số tiền \(y\) (đồng) còn lại khi mua \(x\) kg xoài và cho biết \(y\) có phải là hàm số của \(x\) hay không?
\(y = 210\,000 - 50\,000x\); \(y\) là hàm số của \(x\).
\(y = 210\,000 - 50\,000x\); \(y\) không phải là hàm số của \(x\).
\(y = 210\,000 + 50\,000x\); \(y\) là hàm số của \(x\).
\(y = 210\,000 + 50\,000x\); \(y\) không phải là hàm số của \(x\).
Đáp án : A
Biểu diễn số tiền \(y\) theo \(x\) dựa vào đề bài. Xác định xem \(y\) có phải là hàm số của \(x\) hay không
Số tiền bạn Lan mua \(x\) kg xoài là: \(50\,000.x\) (đồng)
Số tiền \(y\) còn lại khi mua \(x\) kg xoài là: \(y = 210\,000 - 50\,000x\).
Khi đó \(y\) là hàm số của \(x\).
Đáp án A
Điền cụm từ thích hợp vào chỗ trống (…)
Hình thang có … là hình thang cân.
hai cạnh bên bằng nhau.
hai đường chéo bằng nhau.
hai cạnh bên song song.
hai đường chéo vuông góc với nhau.
Đáp án : B
Dựa vào dấu hiệu nhận biết hình thang cân.
Hình thang có hai đường chéo bằng nhau là hình thang cân.
Đáp án B
Phân tích đa thức thành nhân tử:
a) \({x^2} - 9\)
b) \({x^2} - 4x + 4 - {y^2}\)
Áp dụng phương pháp sử dụng hằng đẳng thức để phân tích đa thức thành nhân tử.
a) Sử dụng hằng đẳng thức hiệu hai bình phương.
b) Sử dụng hằng đẳng thức bình phương của một hiệu, sau đó sử dụng hằng đẳng thức hiệu hai bình phương.
a) \({x^2} - 9 = \left( {x - 3} \right)\left( {x + 3} \right)\)
b) \({x^2} - 4x + 4 - {y^2}\)
\(\begin{array}{l} = \left( {{x^2} - 4x + 4} \right) - {y^2}\\ = {\left( {x - 2} \right)^2} - {y^2}\\ = \left( {x - 2 - y} \right)\left( {x - 2 + y} \right)\end{array}\)
Cho biểu thức \(A = \frac{{2x - 3}}{{x - 1}}\) và \(B = \frac{x}{{x - 1}} + \frac{3}{{x + 1}} - \frac{{6x - 4}}{{{x^2} - 1}}\) (với \(x \ne \pm 1\))
a) Tính giá trị của A khi \(x = 2\).
b) Chứng minh rằng biểu thức \(B = \frac{{x - 1}}{{x + 1}}\).
c) Tìm các số nguyên dương \(x\) để biểu thức \(P = A.B\) nhận giá trị là số nguyên.
a) Thay \(x = 2\) vào A để tính giá trị.
b) Quy đồng mẫu để rút gọn biểu thức B.
c) Tính \(P = A.B\), Sử dụng kiến thức về ước và bội, dấu hiệu chia hết để biện luận giá trị biểu thức là số nguyên.
a) Thay \(x = 2\) (thỏa mãn điều kiện) vào A, ta được: \(A = \frac{{2.2 - 3}}{{2 - 1}} = \frac{1}{1} = 1\).
b) Ta có:
\(\begin{array}{l}B = \frac{x}{{x - 1}} + \frac{3}{{x + 1}} - \frac{{6x - 4}}{{{x^2} - 1}}\\ = \frac{{x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \frac{{3\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \frac{{6x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} + x + 3x - 3 - 6x + 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} + \left( {x + 3x - 6x} \right) + \left( { - 3 + 4} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} - 2x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{x - 1}}{{x + 1}}\end{array}\)
Vậy \(B = \frac{{x - 1}}{{x + 1}}\).
c) Ta có:
\(\begin{array}{l}P = A.B = \frac{{2x - 3}}{{x - 1}}.\frac{{x - 1}}{{x + 1}} = \frac{{2x - 3}}{{x + 1}}\\ = \frac{{2x + 2 - 5}}{{x + 1}} = \frac{{2\left( {x + 1} \right) - 5}}{{x + 1}} = 2 - \frac{5}{{x + 1}}\end{array}\)
Để P nguyên thì \(2 - \frac{5}{{x + 1}}\) nguyên, suy ra \(\frac{5}{{x + 1}}\) nguyên.
\(\frac{5}{{x + 1}}\) nguyên khi \(5 \vdots \left( {x + 1} \right)\) hay \(\left( {x + 1} \right) \in \) Ư(5) = \(\left\{ { \pm 1; \pm 5} \right\}\).
Ta có bảng giá trị sau:

Vì \(x\) là số nguyên dương nên \(x = 4\) thỏa mãn.
Vậy biểu thức \(P = A.B\) nhận giá trị là số nguyên khi \(x = 4\).
Một công nhân theo kế hoạch cần phải làm 120 sản phẩm trong một số giờ dự kiến, với số sản phẩm dự kiến làm trong một giờ là \(x\) sản phẩm. Sau khi làm được 2 giờ với năng suất dự kiến, công nhân đó đã tăng năng suất được 3 sản phẩm mỗi giờ, vì vậy công nhân đó đã hoàn thành kế hoạch sớm hơn thời gian dự kiến.
a) Hãy viết biểu thức biểu thị thời gian công nhân đó dự kiến hoàn thành kế hoạch.
b) Hãy viết biểu thức biểu thị thời gian công nhân đó hoàn thành kế hoạch sớm hơn thời gian dự kiến.
a) Áp dụng công thức tính thời gian hoàn thành = tổng số sản phẩm làm được : số sản phẩm làm được trong 1 giờ.
b) Áp dụng công thức tính thời gian hoàn thành = tổng số sản phẩm làm được : số sản phẩm làm được trong 1 giờ.
Thời gian hoàn thành sớm hơn dự kiến = thời gian dự kiến – thời gian hoàn thành thực tế.
a) Biểu thức biểu thị thời gian dự kiến người công nhân đó hoàn thành kế hoạch là: \(\frac{{120}}{x}\) (giờ)
b) Trong 2 giờ công nhân sản xuất với năng suất dự kiến, người công nhân làm được: \(2x\) (sản phẩm).
Khi đó số sản phẩm còn lại là \(120 - 2x\) (sản phẩm)
Sau khi tăng năng suất thì mỗi giờ công nhân sản xuất được: \(x + 3\) sản phẩm.
Người đó sản xuất \(120 - 2x\) trong thời gian là: \(\frac{{120 - 2x}}{{x + 3}}\) (giờ)
Biểu thức biểu thị thời gian thực tế công nhân đó hoàn thành số sản phẩm là: \(2 + \frac{{120 - 2x}}{{x + 3}}\) (giờ)
Vậy biểu thức biểu thị thời gian công nhân đó hoàn thành kế hoạch sớm hơn thời gian dự kiến là:
\(\begin{array}{l}\frac{{120}}{x} - \left( {2 + \frac{{120 - 2x}}{{x + 3}}} \right)\\ = \frac{{120}}{x} - 2 - \frac{{120 - 2x}}{{x + 3}}\\ = \frac{{120\left( {x + 3} \right) - 2x\left( {x + 3} \right) - x\left( {120 - 2x} \right)}}{{x\left( {x + 3} \right)}}\\ = \frac{{120x + 360 - 2{x^2} - 6x - 120x + 2{x^2}}}{{x\left( {x + 3} \right)}}\\ = \frac{{360 - 6x}}{{x\left( {x + 3} \right)}}\end{array}\)
Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của BC và AC. Trên tia đối của tia MN lấy điểm D sao cho MD = MN.
a) Chứng minh tứ giác BDCN là hình bình hành.
b) Chứng minh AD = BN.
c) Cho biết độ dài AM = 5cm, AC = 8cm. Tính diện tích tam giác vuông ABC?
a) Chứng minh BDCN có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Chứng minh ABDN là hình chữ nhật nên hai đường chéo AD và BN bằng nhau.
c) Sử dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông bằng một nửa cạnh huyền để tính BC.
Áp dụng định lí Pythagore để tính AB.
Tính diện tích tam giác vuông bằng \(\frac{1}{2}\) tích hai cạnh góc vuông.
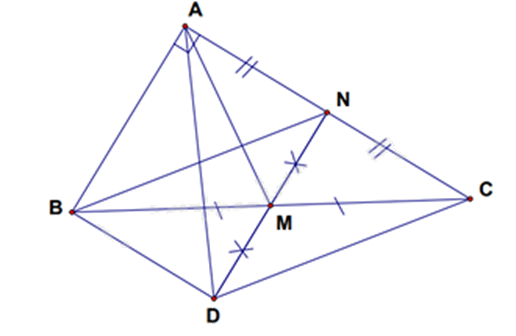
a) Xét tứ giác BNCD có:
M là giao điểm của BC và DN
M là trung điểm của BC (gt)
M là trung điểm của ND (gt)
Suy ra BNCD là hình bình hành.
b) Vì tứ giác BNCD là hình bình hành nên BD // CN, BD = CN.
Mà AN = NC (vì N là trung điểm của AC)
nên BD // AN; BD = AN.
Xét tứ giác ABDN có:
BD // AN; BD = AN
Suy ra ABDN là hình bình hành.
Mà \(\widehat {BAN} = 90^\circ \) nên ABDN là hình chữ nhật.
Suy ra AD = BN
c) Xét tam giác ABC vuông tại A có M là trung điểm của BC nên AN là đường trung tuyến ứng với cạnh huyền nên \(AM = \frac{1}{2}BC\), suy ra \(BC = 2AM = 2.5 = 10\left( {cm} \right)\).
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
\(A{B^2} = B{C^2} - A{C^2} = {10^2} - {8^2} = 100 - 64 = 36\) suy ra \(AB = \sqrt {36} = 6\left( {cm} \right)\).
Vậy diện tích tam giác ABC là:
\({S_{\Delta ABC}} = \frac{1}{2}.AB.AC = \frac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Cho các số \(x,y\) thỏa mãn đẳng thức \(\frac{1}{2}{x^2} + 2{y^2} - x + 2y + 1 = 0\). Tính giá trị của biểu thức \(M = {\left( {x + 2y} \right)^{2022}} + {\left( {x - 2} \right)^{2023}} + {\left( {y + \frac{3}{2}} \right)^{2024}}\).
Biến đổi đẳng thức \(\frac{1}{2}{x^2} + 2{y^2} - x + 2y + 1 = 0\) bằng cách nhân hai vế với 2.
Sử dụng hằng đẳng thức bình phương của một tổng, bình phương của một hiệu để giải tìm x, y.
Thay vào M để tính giá trị của M.
Nhân hai vế của đẳng thức \(\frac{1}{2}{x^2} + 2{y^2} - x + 2y + 1 = 0\) với 2, ta được:
\(\begin{array}{l}2\left( {\frac{1}{2}{x^2} + 2{y^2} - x + 2y + 1} \right) = 0\\{x^2} + 4{y^2} - 2x + 4y + 2 = 0\\\left( {{x^2} - 2x + 1} \right) + \left( {4{y^2} + 4y + 1} \right) = 0\\{\left( {x - 1} \right)^2} + {\left( {2y + 1} \right)^2} = 0\end{array}\)
Vì \({\left( {x - 1} \right)^2} \ge 0\) với mọi x, \({\left( {2y + 1} \right)^2} \ge 0\) với mọi y.
Để \({\left( {x - 1} \right)^2} + {\left( {2y + 1} \right)^2} = 0\) thì \(x - 1 = 0\) và \(2y + 1 = 0\), suy ra \(x = 1\) và \(y = \frac{{ - 1}}{2}\).
Thay vào M, ta được:
\(\begin{array}{l}M = {\left[ {1 + 2.\left( {\frac{{ - 1}}{2}} \right)} \right]^{2022}} + {\left( {1 - 2} \right)^{2023}} + {\left( { - \frac{1}{2} + \frac{3}{2}} \right)^{2024}}\\ = {\left( {1 - 1} \right)^{2022}} + {\left( { - 1} \right)^{2023}} + {1^{2024}}\\ = 0 - 1 + 1 = 0\end{array}\)
Kỳ thi học kì 1 Toán 8 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh. Việc làm quen với các dạng đề thi khác nhau, đặc biệt là các đề thi được biên soạn theo sách Cánh diều, là vô cùng cần thiết. Bài viết này sẽ phân tích chi tiết Đề thi học kì 1 Toán 8 Cánh diều - Đề số 6, cung cấp hướng dẫn giải chi tiết và những lưu ý quan trọng để học sinh đạt kết quả tốt nhất.
Đề thi học kì 1 Toán 8 Cánh diều - Đề số 6 bao gồm các dạng bài tập thuộc chương trình học kì 1, tập trung vào các chủ đề chính như:
Đề thi có cấu trúc đa dạng, kết hợp các câu hỏi trắc nghiệm và tự luận, đòi hỏi học sinh phải nắm vững kiến thức lý thuyết và kỹ năng giải toán.
Chúng ta sẽ đi vào phân tích chi tiết từng câu hỏi trong đề thi, cung cấp hướng dẫn giải cụ thể và những mẹo làm bài hiệu quả.
Phần trắc nghiệm thường tập trung vào các kiến thức cơ bản, đòi hỏi học sinh phải hiểu rõ định nghĩa, tính chất và các quy tắc toán học. Để làm tốt phần này, học sinh cần ôn tập kỹ lý thuyết và luyện tập thường xuyên.
Phần tự luận đòi hỏi học sinh phải trình bày bài giải một cách rõ ràng, logic và chính xác. Để đạt điểm cao, học sinh cần:
Trong đề thi, thường có một số câu hỏi khó đòi hỏi học sinh phải vận dụng kiến thức tổng hợp và kỹ năng giải toán nâng cao. Dưới đây là hướng dẫn giải chi tiết một số câu hỏi khó thường gặp:
Ví dụ: Giải phương trình 2x + 3 = 5
Để đạt kết quả tốt nhất trong kỳ thi học kì 1 Toán 8, học sinh cần:
Đề thi học kì 1 Toán 8 Cánh diều - Đề số 6 là một công cụ hữu ích giúp học sinh ôn luyện và chuẩn bị tốt nhất cho kỳ thi. Hy vọng rằng, với những phân tích chi tiết và hướng dẫn giải cụ thể trong bài viết này, các em sẽ tự tin hơn và đạt kết quả cao trong kỳ thi sắp tới. Chúc các em học tốt!