Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 8 - Đề số 8 - Cánh diều, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 8, tập trung vào các kiến thức trọng tâm và có đáp án chi tiết đi kèm.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và áp dụng kiến thức vào thực tế.
Giải phương trình sau \(\frac{1}{3}x + \frac{1}{2} = x + 2\) ta được:
Lớp trưởng lớp 10A thống kê số học sinh và số cây trồng được theo từng tổ trong buổi ngoại khóa như sau:
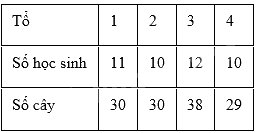
Bạn lớp trưởng cho biết số cây mỗi bạn trong lớp trồng được đều không vượt quá 3 cây. Biết rằng bảng trên có một tổ bị thống kê sai. Tổ mà bạn lớp trưởng đã thống kê sai là:
Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số \(1;2;3;4;5;6;7;8\). Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần Tính xác suất của các biến cố: "Mũi tên chỉ vào hình quạt ghi số là ước của 6".
Chọn đáp án sai. Khi tung đồng xu đồng nhất một lần:
Cho tam giác \({\rm{ABC}},{\rm{AC}} = 2{\rm{AB}},{\rm{AD}}\) là đường phân giác của tam giác \({\rm{ABC}}\), tính \(\frac{{BD}}{{CD}} = \) ?
Cho hình vẽ sau:
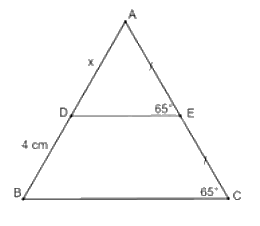
Khẳng định nào sau đây là đúng:
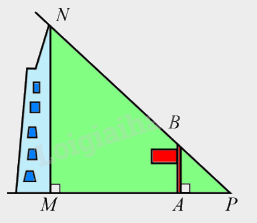
Toà nhà Bitexco Financial (hay tháp tài chính Bitexco) được xây dựng tại trung tâm Quận 1, Thành phố Hồ Chí Minh. Toà nhà có 68 tầng (không kể các tầng hầm). Biết rằng khi toà nhà có bóng MP in trên mặt đất dài \(47,5{\rm{\;m}}\), thì cùng thời điểm đó một cột cờ \({\rm{AB}}\) cao \(12{\rm{\;m}}\) có bóng \({\rm{AP}}\) in trên mặt đất dài \(2,12{\rm{\;m}}\). Tính chiều cao \({\rm{MN}}\) của toà nhà theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
Tổng các nghiệm của hai phương trình \( - 6\left( {1,5 - 2x} \right) = 3\left( { - 15 + 2x} \right);5x + 10 = 0\) bằng:
Một hộp có 1 quả bóng vàng, 1 quả bóng hồng và 1 quả bóng đỏ; các quả bóng có kích thước và khối lượng như nhau . Mỗi lần lấy ngẫu nhiên 1 quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Trong 45 lần lấy bóng liên tiếp, quả bóng vàng xuất hiện 5 lần; quả bóng hồng xuất hiện 10 lần. Tính xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng màu đỏ".
Năm nay, tuổi của mẹ gấp 3 lần tuổi của Hiền. Sau 8 năm nữa, tổng số tuổi của mẹ và của Hiền là 64 tuổi. Hỏi năm nay Hiền bao nhiêu tuổi?
Giải các phương trình sau:a) \(\frac{{9x + 5}}{6} = 1 - \frac{{6 + 3x}}{8}\);b) \(\frac{{x + 1}}{4} = \frac{1}{2} + \frac{{2x + 1}}{5}\);c) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{3}{2} - \frac{{1 - 2x}}{4}\).
Một tàu thuỷ du lịch xuôi dòng từ bến \(A\) đến bến \(B\) mất 2 giờ và ngược dòng từ bến \(B\) về bến \(A\) hết 2,5 giờ. Tính khoảng cách giữa hai bến \(A\) và \(B\), biết rằng vận tốc của dòng nước là \(2{\rm{\;km}}/{\rm{h}}\) và vận tốc riêng của tàu thuỷ là không đổi.
Trong hộp có 5 quả bóng có kích thước và khối lượng giống nhau và được đánh số lần lượt là \(5;8;10;13;16\). Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất của các biến cố:
a) A: "Số ghi trên quả bóng là số lẻ";
b) B: "Số ghi trên quả bóng chia hết cho 3";
c) C: "Số ghi trên quả bóng lớn hơn 4".
Bạn Liên có 5 thẻ ghi riêng từng loại từ trong Tiếng Anh đã học: danh từ (D) , động từ \(\left( {\rm{D}} \right)\), tính từ \(\left( {\rm{T}} \right)\), trạng từ \(\left( {{\rm{Tr}}} \right)\), giới từ \(\left( {\rm{G}} \right)\) và xác định xem thẻ đó có từ thuộc loại nào. Liên lấy ngẫu nhiên 1 thẻ trong số 5 thẻ đó và thực hiện thí nghiệm này 12 lần (trả lại thẻ sau mỗi lần lấy) và thu được kết quả như sau:
a) Tính xác suất thực nghiệm của biến cố "thẻ được lấy ra là trạng từ".
b) Tính xác suất thực nghiệm của biến cố "thẻ được ấy ra là danh từ".
c) Tính xác suất thực nghiệm của biến cố "thẻ được lấy ra là tính từ".
Cho góc \(xAy\) khác góc bẹt. Trên tia Ax lấy các điểm \({\rm{B}},{\rm{C}}\). Qua \({\rm{B}},{\rm{C}}\) vẽ 2 đường thẳng song song cắt \(Ay\) lần lượt ở \(D\) và \(E\). Qua \(E\) vẽ đường thẳng song song với \(CD\) cắt tia \(Ax\) ở \(F\).
a) So sánh \(\frac{{AB}}{{AC}}\) và \(\frac{{AD}}{{AE}};\frac{{AC}}{{AF}}\) và \(\frac{{AD}}{{AE}}\)
b) CMR: \(A{C^2} = AB \cdot AF\)
Giải phương trình sau \(\frac{1}{3}x + \frac{1}{2} = x + 2\) ta được:
Đáp án : B
Chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó (Quy tắc chuyển vế);
Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
\(\frac{1}{3}x + \frac{1}{2} = x + 2\)
\(\frac{1}{3}x - x = 2 - \frac{1}{2}\)
\(\frac{{ - 2}}{3}x = \frac{3}{2}\)
\(x = \frac{3}{2} \cdot \frac{{ - 3}}{2}\)
\(x = \frac{{ - 9}}{4}\)
Đáp án B.
Lớp trưởng lớp 10A thống kê số học sinh và số cây trồng được theo từng tổ trong buổi ngoại khóa như sau:
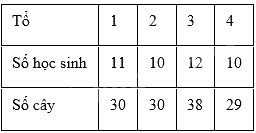
Bạn lớp trưởng cho biết số cây mỗi bạn trong lớp trồng được đều không vượt quá 3 cây. Biết rằng bảng trên có một tổ bị thống kê sai. Tổ mà bạn lớp trưởng đã thống kê sai là:
Đáp án : C
Phân tích số liệu dựa vào bảng thống kê.
Số cây tối đa tổ 1 trồng được là: 11.3 = 33 (cây)
Vì 30 (cây) < 33 (cây) nên thống kê số cây tổ 1 trồng được không sai.
Số cây tối đa tổ 2 trồng được là: \(10.3 = 30\) (cây)
Vì 30 (cây) \( = 30\) (cây) nên thống kê số cây tổ 1 trồng được không sai.
Số cây tối đa tổ 3 trồng được là: \(12.3 = 36\) (cây)
Vì 38 (cây) > 36 (cây) nên thống kê số cây tổ 3 trồng được là sai.
Số cây tối đa tổ 3 trồng được là: \(10.3 = 30\) (cây)
Vì 29 (cây) < 30 (cây) nên thống kê số cây tổ 4 trồng được không sai.
Đáp án C.
Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số \(1;2;3;4;5;6;7;8\). Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần Tính xác suất của các biến cố: "Mũi tên chỉ vào hình quạt ghi số là ước của 6".
Đáp án : D
Trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng, xác suất của một biến cố bằng tỉ số của số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.
Có 4 kết quả thuận lợi cho biến cố "Mũi tên chỉ vào hình quạt ghi số là uớc của 6 " đó là: 1; 2; 3; 6
Vì thế xác suất của biến cố đó là \(\frac{4}{8} = \frac{1}{2}\).
Đáp án D.
Chọn đáp án sai. Khi tung đồng xu đồng nhất một lần:
Đáp án : C
Xác suất của biến cố "Mặt xuất hiện của đồng xu là mặt N" bằng \(\frac{1}{2}\)
Xác suất của biến cố "Mặt xuất hiện của đồng xu là mặt \({\rm{S}}\) " bằng \(\frac{1}{2}\)
Vì khi tung đồng xu đồng nhất một lần ta được 2 kết quả có thể xảy ra là mặt \({\rm{N}}\) hoặc mặt \({\rm{S}}\).
Nên xác suất của biến cố "Mặt xuất hiện của đồng xu là mặt \(S\) " bằng xác suất của biến cố "Mặt xuất hiện của đồng xu là mặt \({\rm{N}}\) " và bằng \(\frac{1}{2}\)
Đáp án C.
Cho tam giác \({\rm{ABC}},{\rm{AC}} = 2{\rm{AB}},{\rm{AD}}\) là đường phân giác của tam giác \({\rm{ABC}}\), tính \(\frac{{BD}}{{CD}} = \) ?
Đáp án : D
Áp dụng tính chất đường phân giác của tam giác để tìm ra tỉ lệ thức phù hợp, từ đó tìm ra kết quả của đề bài.
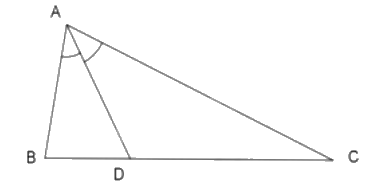
Vì \(AD\) là phân giác của \(\Delta ABC\) nên: \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}\)
Theo bài, ta có: \(AC = 2AB\) suy ra \(\frac{{AB}}{{AC}} = \frac{1}{2}\) hay \(\frac{{BD}}{{DC}} = \frac{1}{2}\)
Đáp án D.
Cho hình vẽ sau:
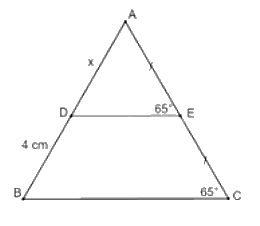
Khẳng định nào sau đây là đúng:
Đáp án : A
Áp dụng hệ quả: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
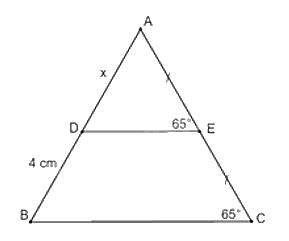
Ta có: \(\widehat {AED} = \widehat {ACB} = {65^0}\)
Mà hai góc này là hai góc ở vị trí đồng vị suy ra \(DE//BC\).
Xét \(\Delta ABC\) có: \(\left\{ {\begin{array}{*{20}{l}}{AE = EC}\\{DE//BD}\end{array}} \right.\)Suy ra \(D\) là trung điểm của \({\rm{AB}}\) (hệ quả) suy ra \(AD = BD = 4{\rm{\;cm}}\)
Đáp án A.
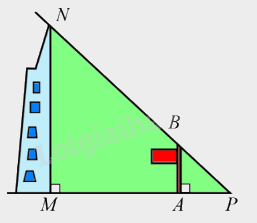
Toà nhà Bitexco Financial (hay tháp tài chính Bitexco) được xây dựng tại trung tâm Quận 1, Thành phố Hồ Chí Minh. Toà nhà có 68 tầng (không kể các tầng hầm). Biết rằng khi toà nhà có bóng MP in trên mặt đất dài \(47,5{\rm{\;m}}\), thì cùng thời điểm đó một cột cờ \({\rm{AB}}\) cao \(12{\rm{\;m}}\) có bóng \({\rm{AP}}\) in trên mặt đất dài \(2,12{\rm{\;m}}\). Tính chiều cao \({\rm{MN}}\) của toà nhà theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
Đáp án : B
Hệ quả định lí Thales: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cąnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Ta có \(\left\{ {\begin{array}{*{20}{l}}{NM \bot MP}\\{BA \bot MP}\end{array}} \right.\) suy ra \(BA\parallel NM\)
Áp dụng hệ quả định lí Thales trong \(\Delta MNP\) có \(\frac{{AB}}{{MN}} = \frac{{AP}}{{MP}}\) hay \(\frac{{12}}{{MN}} = \frac{{2,12}}{{47,5}}\) suy ra \(MN = \frac{{12.47,5}}{{2,12}} \approx 269\left( {{\rm{\;m}}} \right)\)
Vậy chiều cao \({\rm{MN}}\) của toà nhà khoảng \(269{\rm{\;m}}\) (đã làm tròn kết quả đến hàng đơn vị)
Đáp án B.
Tổng các nghiệm của hai phương trình \( - 6\left( {1,5 - 2x} \right) = 3\left( { - 15 + 2x} \right);5x + 10 = 0\) bằng:
Đáp án : A
Giải lần lượt từng phương trình:
Chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó (Quy tắc chuyển vế);
Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
Sau đó cộng các nghiệm lại theo yêu cầu.
PT1: \( - 6\left( {1,5 - 2x} \right) = 3\left( { - 15 + 2x} \right)\)
\( - 2\left( {1,5 - 2x} \right) = - 15 + 2x\)
\( - 3 + 4x = - 15 + 2x\)
\(4x - 2x = - 15 + 3\)
\(2x = - 12\)
\(x = - 6\)
PT2: \(5x + 10 = 0\)
\(5x = - 10\)
\(x = - 2\)
Ta có tổng các nghiệm của hai phương trình trên là \( - 6 + \left( { - 2} \right) = - 8\)
Đáp án A.
Một hộp có 1 quả bóng vàng, 1 quả bóng hồng và 1 quả bóng đỏ; các quả bóng có kích thước và khối lượng như nhau . Mỗi lần lấy ngẫu nhiên 1 quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Trong 45 lần lấy bóng liên tiếp, quả bóng vàng xuất hiện 5 lần; quả bóng hồng xuất hiện 10 lần. Tính xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng màu đỏ".
Đáp án : C
Xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng màu đỏ" bằng tỉ số số lần xuất hiện quả bóng màu đỏ và số lần lấy bóng liên tiếp.
Trong 45 lần lấy bóng liên tiếp, quả bóng vàng xuất hiện 5 lần; quả bóng hồng xuất hiện 10 lần.
Suy ra số lần quả bóng đỏ xuất hiện là \(45 - 5 - 10 = 30\) lần
Xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng màu đỏ" là \(\frac{{30}}{{45}} = \frac{2}{3}\)
Đáp án C.
Năm nay, tuổi của mẹ gấp 3 lần tuổi của Hiền. Sau 8 năm nữa, tổng số tuổi của mẹ và của Hiền là 64 tuổi. Hỏi năm nay Hiền bao nhiêu tuổi?
Đáp án : B
Bước 1. Lập phương trình.
Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết.
Lập phương trình biểu diễn mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Trả lời.
Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không.
Kết luận.
Gọi số tuổi của Hiền năm nay là \(x\) (tuổi). Điều kiện \(x \in {\mathbb{N}^{\rm{*}}}\)
Năm nay số tuổi của mẹ là \(3x\) (tuổi)
Tuổi của Hiền 8 năm nữa là \(x + 8\) (tuổi)
Tuổi của mẹ 8 năm nữa là \(3x + 8\) (tuổi)
Vì sau 8 năm nữa, tổng số tuổi của mẹ và của Hiền là 64 tuổi nên ta có PT:
\(x + 8 + 3x + 8 = 64\)
\(4x = 64 - 8 - 8\)
\(4x = 48\)
\(x = 12\left( {TM} \right)\)
Vậy năm nay Hiền 12 tuổi
Đáp án B.
Giải các phương trình sau:a) \(\frac{{9x + 5}}{6} = 1 - \frac{{6 + 3x}}{8}\);b) \(\frac{{x + 1}}{4} = \frac{1}{2} + \frac{{2x + 1}}{5}\);c) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{3}{2} - \frac{{1 - 2x}}{4}\).
Chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó (Quy tấc chuyển vế);
Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
a) \(\frac{{9x + 5}}{6} = 1 - \frac{{6 + 3x}}{8}\)
\(\frac{{4\left( {9x + 5} \right)}}{{24}} = \frac{{24}}{{24}} - \frac{{3\left( {6 + 3x} \right)}}{{24}}\)
\(36x + 20 = 24 - 18 - 9x\)
\(36x + 9x = 6 - 20\)
\(45x = - 14\)
\(x = \frac{{ - 14}}{{45}}\)
Vậy \(x = \frac{{ - 14}}{{45}}\)b) \(\frac{{x + 1}}{4} = \frac{1}{2} + \frac{{2x + 1}}{5}\)
\(5x + 5 = 10 + 8x + 4\)
\(5x - 8x = 14 - 5\)
\( - 3x = 9\)
\(x = - 3\)
Vậy \(x = - 3\)c) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{3}{2} - \frac{{1 - 2x}}{4}\)
\(\frac{{8\left( {x + 1} \right)}}{{12}} = \frac{{18}}{{12}} - \frac{{3\left( {1 - 2x} \right)}}{{12}}\)
\(8x + 8 = 18 - 3 + 6x\)
\(8x - 6x = 15 - 8\)
\(2x = 7\)
\(x = \frac{7}{2}\)
Vậy \(x = \frac{7}{2}\)
Một tàu thuỷ du lịch xuôi dòng từ bến \(A\) đến bến \(B\) mất 2 giờ và ngược dòng từ bến \(B\) về bến \(A\) hết 2,5 giờ. Tính khoảng cách giữa hai bến \(A\) và \(B\), biết rằng vận tốc của dòng nước là \(2{\rm{\;km}}/{\rm{h}}\) và vận tốc riêng của tàu thuỷ là không đổi.
Bước 1: Lập phương trình:
Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số;
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
Vận tốc xuôi dòng = vận tốc riêng + vận tốc dòng nước, vận tốc ngược dòng = vận tốc riêng - vận tốc dòng nước.
Gọi vận tốc riêng của tàu thủy là \(x\left( {{\rm{\;km}}/{\rm{h}}} \right)\), điều kiện: \(x > 2\)
Vận tốc xuôi dòng của tàu thủy là: \(x + 2\left( {{\rm{\;km}}/{\rm{h}}} \right)\)
Vận tốc ngược dòng của tàu thủy là: \(x - 2\left( {{\rm{\;km}}/{\rm{h}}} \right)\)
Quãng đường từ bến \(A\) đến bến \(B\) là: \(2\left( {x + 2} \right)\left( {{\rm{km}}} \right)\)
Quãng đường từ bến \(B\) đến bến \(A\) là: 2,5( \(x - 2)\left( {{\rm{km}}} \right)\)
Ta có phương trình: \(2\left( {x + 2} \right) = 2,5\left( {x - 2} \right)\)
\(\begin{array}{*{20}{r}}{}&{2x + 4 = 2,5x - 5}\\{}&{0,5x = 9}\\{}&{x = 18\left( {{\rm{TM}}} \right)}\end{array}\)
Vậy khoảng cách giữa hai bến \(A\) và \(B\) là: \(2\left( {18 + 2} \right) = 40\left( {{\rm{\;km}}} \right)\)
Trong hộp có 5 quả bóng có kích thước và khối lượng giống nhau và được đánh số lần lượt là \(5;8;10;13;16\). Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất của các biến cố:
a) A: "Số ghi trên quả bóng là số lẻ";
b) B: "Số ghi trên quả bóng chia hết cho 3";
c) C: "Số ghi trên quả bóng lớn hơn 4".
Trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng, xác suất của một biến cố bằng tỉ số của số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.
Có 5 kết quả có thể xảy ra.
a) Có 2 kết quả thuận lợi cho biến cố \({\rm{A}}\) là 5; 13
Xác suất của biến cố \({\rm{A}}\) là \(\frac{2}{5}\)
b) Có 0 kết quả thuận lợi cho biến cố \({\rm{B}}\)
Xác suất của biến cố \({\rm{B}}\) là 0
c) Có 5 kết quả thuận lợi cho biến cố \({\rm{C}}\)
Xác suất của biến cố \({\rm{C}}\) là 1
Bạn Liên có 5 thẻ ghi riêng từng loại từ trong Tiếng Anh đã học: danh từ (D) , động từ \(\left( {\rm{D}} \right)\), tính từ \(\left( {\rm{T}} \right)\), trạng từ \(\left( {{\rm{Tr}}} \right)\), giới từ \(\left( {\rm{G}} \right)\) và xác định xem thẻ đó có từ thuộc loại nào. Liên lấy ngẫu nhiên 1 thẻ trong số 5 thẻ đó và thực hiện thí nghiệm này 12 lần (trả lại thẻ sau mỗi lần lấy) và thu được kết quả như sau:
a) Tính xác suất thực nghiệm của biến cố "thẻ được lấy ra là trạng từ".
b) Tính xác suất thực nghiệm của biến cố "thẻ được ấy ra là danh từ".
c) Tính xác suất thực nghiệm của biến cố "thẻ được lấy ra là tính từ".
a) Xác suất thực nghiệm của biến cố "thẻ được lấy ra là trạng từ" là tỉ số giữa số lần xuất hiện thẻ là trạng từ và tổng số lần rút thẻ.
b) Xác suất thực nghiệm của biến cố "thẻ được lấy ra là danh từ" là tỉ số giữa số lần xuất hiện thẻ là danh từ và tổng số lần rút thẻ.
c) Xác suất thực nghiệm của biến cố "thẻ được lấy ra là tính từ" là tỉ số giữa số lần xuất hiện thẻ là trạng từ và tổng số lần rút thẻ.
Có 12 lấy thẻ.
a) Có 4 lần xuất hiện thẻ là trạng từ \(\left( {{\rm{Tr}}} \right)\)
Xác suất thực nghiệm của biến cố "thẻ được lấy ra là trạng từ" là \(\frac{4}{{12}} = \frac{1}{3}\)
b) Có 2 lần xuất hiện thẻ là danh từ (D)
Xác suất thực nghiệm của biến cố "thẻ được lấy ra là danh từ" là \(\frac{2}{{12}} = \frac{1}{6}\)
c) Có 1 lần xuất hiện thẻ là tính từ \(\left( {\rm{T}} \right)\)
Xác suất thực nghiệm của biến cố "thẻ được lấy ra là tính từ" là \(\frac{1}{{12}}\)
Cho góc \(xAy\) khác góc bẹt. Trên tia Ax lấy các điểm \({\rm{B}},{\rm{C}}\). Qua \({\rm{B}},{\rm{C}}\) vẽ 2 đường thẳng song song cắt \(Ay\) lần lượt ở \(D\) và \(E\). Qua \(E\) vẽ đường thẳng song song với \(CD\) cắt tia \(Ax\) ở \(F\).
a) So sánh \(\frac{{AB}}{{AC}}\) và \(\frac{{AD}}{{AE}};\frac{{AC}}{{AF}}\) và \(\frac{{AD}}{{AE}}\)
b) CMR: \(A{C^2} = AB \cdot AF\)
a) Áp dụng định lí Thales để so sánh tỉ số các cặp cạnh đã cho.
b) Áp dụng tính chất bắc cầu để suy ra biểu thức cần chứng minh.
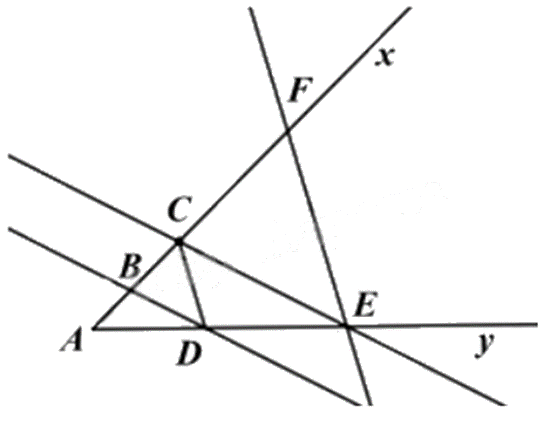
a) Vì \({\rm{BD}}//{\rm{CE}}\), áp dụng định lý Talet ta có: \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AE}}\)
Vì \({\rm{CD}}//{\rm{EF}}\), áp dụng định lý Talet ta có: \(\frac{{AC}}{{AF}} = \frac{{AD}}{{AE}}\)
b) Từ (1) và (2) ta có:
\(\frac{{AB}}{{AC}} = \frac{{AC}}{{AF}}\) suy ra \(AC \cdot AC = AB \cdot AF\)hay \(A{C^2} = AB \cdot AF\) (điều phải chứng minh)
Đề thi giữa kì 2 Toán 8 - Đề số 8 - Cánh diều là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kỳ. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính như đa thức, phân thức đại số, phương trình bậc nhất một ẩn, bất phương trình bậc nhất một ẩn, hệ phương trình bậc nhất hai ẩn, và các ứng dụng thực tế của đại số.
Thông thường, đề thi giữa kì 2 Toán 8 - Cánh diều có cấu trúc như sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 2 Toán 8 - Đề số 8 - Cánh diều:
Các bài tập về đa thức thường yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia đa thức, phân tích đa thức thành nhân tử, và giải các bài toán liên quan đến đa thức. Các bài tập về phân thức đại số thường yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia phân thức, rút gọn phân thức, và giải các bài toán liên quan đến phân thức.
Các bài tập về phương trình bậc nhất một ẩn thường yêu cầu học sinh giải phương trình, tìm nghiệm của phương trình, và giải các bài toán ứng dụng của phương trình.
Các bài tập về bất phương trình bậc nhất một ẩn thường yêu cầu học sinh giải bất phương trình, tìm tập nghiệm của bất phương trình, và giải các bài toán ứng dụng của bất phương trình.
Các bài tập về hệ phương trình bậc nhất hai ẩn thường yêu cầu học sinh giải hệ phương trình, tìm nghiệm của hệ phương trình, và giải các bài toán ứng dụng của hệ phương trình.
Để giải tốt đề thi giữa kì 2 Toán 8 - Đề số 8 - Cánh diều, học sinh cần:
Để chuẩn bị tốt nhất cho đề thi giữa kì 2 Toán 8 - Đề số 8 - Cánh diều, học sinh có thể tham khảo các tài liệu sau:
Đề thi giữa kì 2 Toán 8 - Đề số 8 - Cánh diều là một cơ hội tốt để học sinh đánh giá năng lực bản thân và chuẩn bị cho các kỳ thi tiếp theo. Hy vọng rằng với những thông tin và hướng dẫn trên, các em sẽ tự tin và đạt kết quả tốt nhất trong kỳ thi sắp tới.