Giaitoan.edu.vn xin giới thiệu Đề thi học kì 2 Toán 8 - Đề số 4 - Cánh diều, một công cụ ôn tập vô cùng hữu ích dành cho các em học sinh. Đề thi được biên soạn theo chương trình học Toán 8, tập trung vào các kiến thức trọng tâm và thường xuyên xuất hiện trong đề thi chính thức.
Với cấu trúc đề thi đa dạng, bao gồm các dạng bài tập khác nhau, đề thi này sẽ giúp các em rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Trong các phương trình sau, phương trình bậc nhất một ẩn là
Nghiệm của phương trình \(4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\) là?
Phương trình bậc nhất một ẩn \(ax + b = 0\left( {a \ne 0} \right)\). Hạng tử tự do là
Phương trình nào dưới đây chỉ có một nghiệm
Gọi \(x\) (km) là chiều dài quãng đường AB. Một xe máy đi từ A đến B với vận tốc 40 km/h và đi từ B về A với vận tốc 50 km/h. Biểu thức biểu thị tổng thời gian xe máy đi từ A đến B và từ B về A là
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu:
Cho $\Delta ABC\backsim \Delta A'B'C'$. Khẳng định nào sau đây là sai?
Điều kiện để $\Delta ABC\backsim \Delta DEF$ theo trường hợp cạnh – góc – cạnh nếu \(\widehat B = \widehat E\) là:
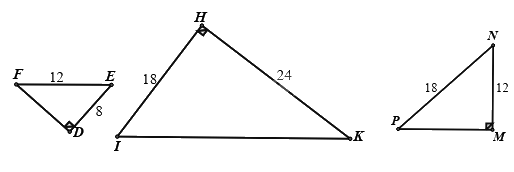
Trong hình dưới đây, các tam giác nào đồng dạng với nhau là
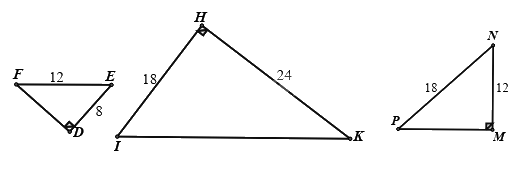
Cho hình vẽ sau, giá trị của x là:
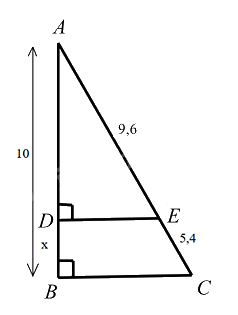
Trong các hình sau, cặp hình nào không phải luôn đồng dạng?
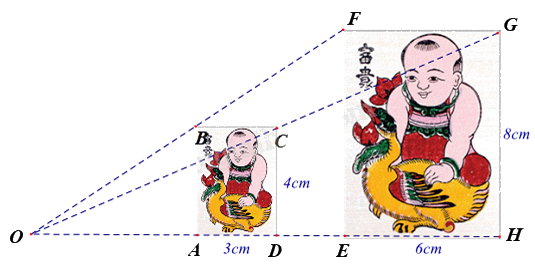
Hình ABCD đồng dạng phối cảnh với hình EFGH theo tỉ số đồng dạng là
Giải các phương trình sau:
a) \(8 + 2\left( {x - 1} \right) = 20\)
b) \(4\left( {3x - 2} \right) + 3\left( {x - 4} \right) = 7x + 20\)
c) \(\frac{{2x}}{3} + x = \frac{{2x + 5}}{6} + \frac{1}{2}\)
Giải bài toán bằng cách lập phương trình
Một xí nghiệp kí hợp đồng dệt một số tấm thảm len trong 17 ngày. Do cải tiến kĩ thuật, năng suất mỗi ngày tăng thêm 7 tấm nên không những xí nghiệp đã hoàn thành kế hoạch sớm hơn 2 ngày mà còn dệt được thêm 7 tấm. Tính số thảm len mà xí nghiệp phải dệt theo hợp đồng.
Cho \(\Delta ABC\) nhọn (AB < AC). Hai đường cao BE và CF.
a) Chứng minh $\Delta ABE\backsim \Delta ACF$ và \(AE.AC = AF.AB\)
b) Trên tia BE lấy điểm N sao cho \(\widehat {ANC} = {90^0}\) (E nằm giữa B và N). Chứng minh $\Delta ANE\backsim \Delta ACN$ và \(A{N^2} = AE.AC\).
c) Trên cạnh CF lấy điểm M sao cho AM = AN. Tính số đo \(\widehat {AMB}\).
Tiểu sử của nhà toán học cổ đại nổi tiếng Diophante được tóm tắt trên bia mộ của ông như sau: “Hỡi người qua đường! Đây là nơi chôn cất di hài của Diophante, người mà một phần sáu cuộc đời là tuổi niên thiếu huy hoàng; một phần mười hai cuộc đời nữa trôi qua, trên cằm đã mọc râu lún phún. Diophante lấy vợ, một phần bảy cuộc đời trong cảnh vợ chồng hiếm hoi. Năm năm trôi qua, ông sung sướng khi có cậu con trai đầu lòng khôi ngô. Nhưng cậu ta chỉ sống được bằng nửa cuộc đời đẹp đẽ của cha. Rút cục thì nỗi buồn thương sâu sắc, ông chỉ sống thêm được 4 năm nữa từ sau khi cậu ta lìa đời.” Tính tuổi thọ của Diophante.
Giải phương trình \(\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16\).
Trong các phương trình sau, phương trình bậc nhất một ẩn là
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\).
Phương trình bậc nhất một ẩn là phương trình \(3x + 2 = 0\).
Đáp án B.
Nghiệm của phương trình \(4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\) là?
Đáp án : B
Đưa phương trình về dạng \(ax + b = 0\) để giải.
\(\begin{array}{l}4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\\4x - 4 - x + 2 = - x\\3x - 2 = - x\\3x + x = 2\\4x = 2\\x = \frac{1}{2}\end{array}\)
Vậy \(x = \frac{1}{2}\)
Đáp án B.
Phương trình bậc nhất một ẩn \(ax + b = 0\left( {a \ne 0} \right)\). Hạng tử tự do là
Đáp án : B
Dựa vào kiến thức về phương trình bậc nhất một ẩn.
Phương trình bậc nhất một ẩn \(ax + b = 0\left( {a \ne 0} \right)\) có hạng tử tự do là b.
Đáp án B.
Phương trình nào dưới đây chỉ có một nghiệm
Đáp án : C
Đưa phương trình về dạng ax + b = 0 để giải phương trình.
Ta có:
\(\begin{array}{l}4x - 1 = 4x + 3\\4x - 4x = 3 + 1\end{array}\)
\(0x = 4\) (vô lí)
Phương trình \(4x - 1 = 4x + 3\) vô nghiệm
Giải tương tự, ta được:
Phương trình \(5 + 2x = 2x - 5\) vô nghiệm;
Phương trình \(3x - 2x = 3x + 1\) có nghiệm duy nhất là \(x = - \frac{1}{2}\);
Phương trình \(x - 7x = 1 - 6x\) vô nghiệm.
Đáp án C.
Gọi \(x\) (km) là chiều dài quãng đường AB. Một xe máy đi từ A đến B với vận tốc 40 km/h và đi từ B về A với vận tốc 50 km/h. Biểu thức biểu thị tổng thời gian xe máy đi từ A đến B và từ B về A là
Đáp án : A
Biểu thị thời gian đi và về theo x.
Thời gian xe máy đi từ A đến B là: \(\frac{x}{{40}}\) (h)
Thời gian xe máy đi từ B về A là: \(\frac{x}{{50}}\) (h)
Vậy biểu thức biểu thị tổng thời gian xe máy đi từ A đến B và từ B về A là: \(\frac{x}{{40}} + \frac{x}{{50}}\).
Đáp án A.
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu:
Đáp án : D
Dựa vào trường hợp đồng dạng góc – góc của hai tam giác.
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
Đáp án D.
Cho $\Delta ABC\backsim \Delta A'B'C'$. Khẳng định nào sau đây là sai?
Đáp án : A
Dựa vào tính chất của hai tam giác đồng dạng.
Vì $\Delta ABC\backsim \Delta A'B'C'$ nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}\) hay \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\) suy ra B, C, D đúng.
Đáp án A.
Điều kiện để $\Delta ABC\backsim \Delta DEF$ theo trường hợp cạnh – góc – cạnh nếu \(\widehat B = \widehat E\) là:
Đáp án : B
Dựa vào trường hợp đồng dạng cạnh – góc – cạnh.
Để $\Delta ABC\backsim \Delta DEF$ theo trường hợp cạnh – góc – cạnh thì \(\widehat B = \widehat E\) và \(\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}}\).
Đáp án B.
Trong hình dưới đây, các tam giác nào đồng dạng với nhau là
Đáp án : B
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.
Xét \(\Delta DEF\) và \(\Delta MNP\) có:
\(\begin{array}{l}\widehat D = \widehat M = {90^0}\\\frac{{DE}}{{MN}} = \frac{{EF}}{{NP}}\left( {\frac{8}{{12}} = \frac{{12}}{{18}}\left( { = \frac{2}{3}} \right)} \right)\end{array}\)
nên $\Delta DEF\backsim \Delta MNP$(cạnh huyền – cạnh góc vuông)
Áp dụng định lí Pythagore vào tam giác HIK có:
\(KI = \sqrt {{{18}^2} + {{24}^2}} = 30\)
Vì \(\frac{8}{{12}} = \frac{2}{3} \ne \frac{{18}}{{30}} = \frac{3}{5}\) nên \(\Delta DEF\) không đồng dạng với \(\Delta HIK\).
Điều này dẫn đến \(\Delta MNP\) không đồng dạng với \(\Delta HIK\)(vì $\Delta DEF\backsim \Delta MNP$)
Đáp án B.
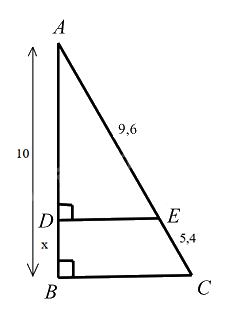
Cho hình vẽ sau, giá trị của x là:
Đáp án : B
Dựa vào kiến thức về hai tam giác vuông đồng dạng để tìm x.
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
\(\widehat B = \widehat D = {90^0}\)
\(\widehat A\) chung
Suy ra $\Delta ABC\backsim \Delta ADE$ (g.g)
Do đó \(\frac{{AB}}{{BC}} = \frac{{AD}}{{DE}}\) hay \(\frac{{10}}{{9,6 + 5,4}} = \frac{{AD}}{{9,6}}\)
Suy ra \(AD = 9,6.\frac{{10}}{{9,6 + 5,4}} = 6,4\)
Vậy \(x = AB - AD = 10 - 6,4 = 3,6\).
Đáp án B.
Trong các hình sau, cặp hình nào không phải luôn đồng dạng?
Đáp án : A
Dựa vào đặc điểm của các hình để xác định.
Tam giác cân không phải luôn đồng dạng.
Đáp án A.
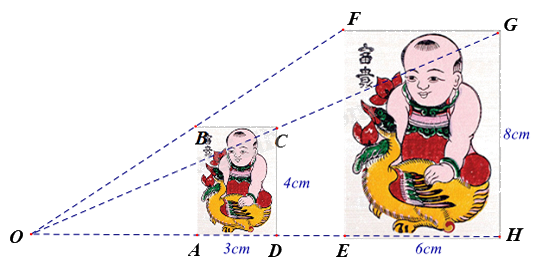
Hình ABCD đồng dạng phối cảnh với hình EFGH theo tỉ số đồng dạng là
Đáp án : A
Dựa vào số đo các cạnh để tìm tỉ số.
Ta có: \(\frac{3}{6} = \frac{4}{8} = \frac{1}{2}\) nên hình ABCD đồng dạng phối cảnh với hình EFGH theo tỉ số đồng dạng là \(k = \frac{1}{2}\).
Đáp án A.
Giải các phương trình sau:
a) \(8 + 2\left( {x - 1} \right) = 20\)
b) \(4\left( {3x - 2} \right) + 3\left( {x - 4} \right) = 7x + 20\)
c) \(\frac{{2x}}{3} + x = \frac{{2x + 5}}{6} + \frac{1}{2}\)
Đưa phương trình về dạng \(ax + b = 0\) để giải.
a) \(8 + 2\left( {x - 1} \right) = 20\)
\(\begin{array}{l}8 + 2x - 2 = 20\\2x + 6 = 20\\2x = 20 - 6\\2x = 14\\x = 7\end{array}\)
Vậy \(x = 7\)
b) \(4\left( {3x - 2} \right) + 3\left( {x - 4} \right) = 7x + 20\)
\(\begin{array}{l}12x - 8 + 3x - 12 = 7x + 20\\12x + 3x - 7x = 20 + 8 + 12\\8x = 40\\x = 5\end{array}\)
Vậy \(x = 5\)
c) \(\frac{{2x}}{3} + x = \frac{{2x + 5}}{6} + \frac{1}{2}\)
\(\begin{array}{l}\frac{{2.2x}}{6} + \frac{{6x}}{6} = \frac{{2x + 5}}{6} + \frac{3}{6}\\4x + 6x = 2x + 5 + 3\\10x - 2x = 8\\8x = 8\\x = 1\end{array}\)
Vậy \(x = 1\)
Giải bài toán bằng cách lập phương trình
Một xí nghiệp kí hợp đồng dệt một số tấm thảm len trong 17 ngày. Do cải tiến kĩ thuật, năng suất mỗi ngày tăng thêm 7 tấm nên không những xí nghiệp đã hoàn thành kế hoạch sớm hơn 2 ngày mà còn dệt được thêm 7 tấm. Tính số thảm len mà xí nghiệp phải dệt theo hợp đồng.
Giải bài toán bằng cách lập phương trình.
Gọi số thảm xí nghiệp phải dệt trong 1 ngày theo hợp đồng là x (tấm) (x > 0)
Biểu diễn năng suất mỗi ngày của xí nghiệp, số thảm theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi số thảm xí nghiệp phải dệt trong 1 ngày theo hợp đồng là x (tấm) (x > 0)
Thực tế một ngày xí nghiệp dệt được: x + 7 (tấm)
Số thảm len mà xí nghiệp phải dệt theo hợp đồng là: 17x (tấm)
Thực tế số thảm xí nghiệp dệt được là:
(17 – 2).(x + 7) = 15(x + 7) (tấm)
Theo bài ra ta có phương trình:
\(15(x + 7) = 17x + 7\)
Giải phương trình ta được: \(x = 49\) (thỏa mãn)
Vậy số thảm len xí nghiệp phải dệt theo hợp đồng là: 17.49 = 833 (tấm)
Cho \(\Delta ABC\) nhọn (AB < AC). Hai đường cao BE và CF.
a) Chứng minh $\Delta ABE\backsim \Delta ACF$ và \(AE.AC = AF.AB\)
b) Trên tia BE lấy điểm N sao cho \(\widehat {ANC} = {90^0}\) (E nằm giữa B và N). Chứng minh $\Delta ANE\backsim \Delta ACN$ và \(A{N^2} = AE.AC\).
c) Trên cạnh CF lấy điểm M sao cho AM = AN. Tính số đo \(\widehat {AMB}\).
a) Chứng minh $\Delta ABE\backsim \Delta ACF$ theo trường hợp góc – góc suy ra tỉ số các cạnh tương ứng suy ra \(AE.AC = AF.AB\).
b) Chứng minh $\Delta ANB\backsim \Delta ENA$ (g.g) suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra \(A{N^2} = NE.NB\).
c) Dựa vào các tỉ số của câu a và b suy ra \(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\) suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$.
Từ đó suy ra số đo góc AMB.
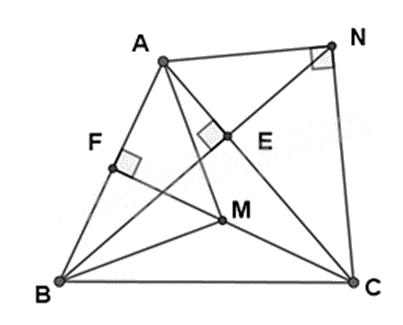
a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat {AEB} = \widehat {AFC} = {90^0}\)
\(\widehat {BAC}\) chung
Suy ra $\Delta ABE\backsim \Delta ACF$ (g.g). (đpcm)
Suy ra \(\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\) hay \(AB.AF = AE.AC\)(đpcm) (1)
b) Xét \(\Delta ANE\) và \(\Delta ACN\) có:
\(\widehat {AEN} = \widehat {ANC} = {90^0}\)
\(\widehat {NAC}\) chung
Suy ra $\Delta ANE\backsim \Delta ACN$ (g.g).
Suy ra \(\frac{{AN}}{{AC}} = \frac{{AE}}{{AN}}\) hay \(A{N^2} = AC.AE\) (đpcm). (2)
c) Từ (1) và (2) suy ra \(AB.AF = A{N^2}\).
Mà AM = AN (gt) suy ra \(AM = AB.AF\) hay \(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\).
Xét \(\Delta AMF\) và \(\Delta ABM\) có:
\(\widehat {BAM}\) chung
\(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\) (cmt)
Suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$
Suy ra \(\widehat {AMB} = \widehat {AFM} = {90^0}\).
Tiểu sử của nhà toán học cổ đại nổi tiếng Diophante được tóm tắt trên bia mộ của ông như sau: “Hỡi người qua đường! Đây là nơi chôn cất di hài của Diophante, người mà một phần sáu cuộc đời là tuổi niên thiếu huy hoàng; một phần mười hai cuộc đời nữa trôi qua, trên cằm đã mọc râu lún phún. Diophante lấy vợ, một phần bảy cuộc đời trong cảnh vợ chồng hiếm hoi. Năm năm trôi qua, ông sung sướng khi có cậu con trai đầu lòng khôi ngô. Nhưng cậu ta chỉ sống được bằng nửa cuộc đời đẹp đẽ của cha. Rút cục thì nỗi buồn thương sâu sắc, ông chỉ sống thêm được 4 năm nữa từ sau khi cậu ta lìa đời.” Tính tuổi thọ của Diophante.
Gọi tuổi thọ của nhà toán học Diphante là x, \(x \in N*\).
Biểu diễn các đại lượng theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi tuổi thọ của nhà toán học Diphante là x (tuổi), \(x \in N*\).
Tuổi niên thiếu của ông là \(\frac{1}{6}x\)
Thời thanh niên của ông là \(\frac{1}{{12}}x\)
Thời vợ chồng chưa có con là: \(\frac{1}{7}x\)
Tuổi của con trai ông là: \(\frac{1}{2}x\)
Theo bài ra ta có phương trình:
\(\frac{1}{6}x + \frac{1}{{12}}x + \frac{1}{7}x + 5 + \frac{1}{2}x + 4 = x\)
Giải phương trình ta được \(x = 84\left( {TM} \right)\)
Vậy tuổi thọ của Diophante là 84 tuổi
Giải phương trình \(\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16\).
Nhân cả hai vế của phương trình với 9, phương trình trở thành \(\left( {3x - 2} \right){\left( {3x + 3} \right)^2}\left( {3x + 8} \right) = - 144\).
Đặt \(3x + 3 = t\), biến đổi phương trình thành \(\left( {t - 5} \right){t^2}\left( {t + 5} \right) = - 144\).
Giải phương trình ta được các giá trị của t.
Thay \(t = 3x + 3\) ta tìm đc x.
Nhân cả hai vế của phương trình \(\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16\) với 9, ta được:
\(\begin{array}{l}9.\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16.9\\\left( {3x - 2} \right){\left[ {3\left( {x + 1} \right)} \right]^2}\left( {3x + 8} \right) = - 144\\\left( {3x - 2} \right){\left( {3x + 3} \right)^2}\left( {3x + 8} \right) = - 144\end{array}\)
Đặt \(3x + 3 = t\) suy ra \(3x - 2 = t - 5\); \(3x + 8 = t + 5\)
Ta được phương trình biến t như sau:
\(\left( {t - 5} \right){t^2}\left( {t + 5} \right) = - 144\)
\(\begin{array}{l}{t^4} - 25{t^2} + 144 = 0\\\left( {{t^2} - 9} \right)\left( {{t^2} - 16} \right) = 0\\\left[ \begin{array}{l}{t^2} = 9\\{t^2} = 16\end{array} \right.\\\left[ \begin{array}{l}t = \pm 3\\t = \pm 4\end{array} \right.\end{array}\)
Thay \(t = 3x + 3\) ta được:

Vậy nghiệm của phương trình là \(x \in \left\{ {0; - 2;\frac{1}{3};\frac{{ - 7}}{3}} \right\}\).
Đề thi học kì 2 Toán 8 - Đề số 4 - Cánh diều là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một học kỳ học tập. Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, đòi hỏi học sinh phải có sự hiểu biết sâu sắc về các khái niệm và định lý Toán 8.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi học kì 2 Toán 8 - Đề số 4 - Cánh diều bao gồm:
Để đạt kết quả tốt trong kỳ thi học kì 2 Toán 8, học sinh cần:
Bài 1: Giải phương trình 2x + 3 = 7
Lời giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Để hỗ trợ quá trình ôn tập, học sinh có thể tham khảo các tài liệu sau:
Hãy dành thời gian ôn tập kỹ lưỡng và làm quen với các dạng bài tập thường gặp trong đề thi. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi học kì 2 Toán 8!
Trong đề thi học kì 2 Toán 8 - Đề số 4 - Cánh diều, các bài tập về phân tích đa thức thành nhân tử thường đòi hỏi học sinh phải nắm vững các phương pháp như đặt nhân tử chung, sử dụng hằng đẳng thức, nhóm đa thức. Việc luyện tập các bài tập này sẽ giúp học sinh rèn luyện kỹ năng tư duy và khả năng biến đổi đại số.
Toán 8 không chỉ là một môn học lý thuyết mà còn có nhiều ứng dụng trong thực tế. Ví dụ, việc giải phương trình bậc nhất một ẩn có thể giúp chúng ta tính toán các đại lượng trong các bài toán thực tế như tính tiền, tính quãng đường, tính thời gian. Do đó, việc học tốt Toán 8 sẽ giúp chúng ta có thêm những công cụ hữu ích để giải quyết các vấn đề trong cuộc sống.
| Chủ đề | Mức độ quan trọng |
|---|---|
| Đa thức | Cao |
| Phân thức đại số | Trung bình |
| Phương trình | Cao |
| Nguồn: Giaitoan.edu.vn | |