Giaitoan.edu.vn xin giới thiệu Đề thi học kì 2 Toán 8 - Đề số 2 - Cánh diều, một công cụ hỗ trợ học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 8, tập trung vào các kiến thức trọng tâm và các dạng bài tập thường gặp.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Phương trình \(3x + m - x - 1 = 0\) nhận \(x = - 3\) là nghiệm thì m là:
Một ô tô đi từ A đến B từ 6 giờ sáng, lúc 7 giờ sáng cùng ngày, một xe khách cũng đi từ A và tới B cùng lúc với ô tô. Vậy nếu gọi thời gian đi của xe khách là x ( giờ) thì thời gian đi của ô tô là:
Năm nay tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương. Gọi x là tuổi của Phương năm nay vậy thì phương trình tìm x là
Cho công thức \(C = \frac{5}{9}\left( {F - 32} \right)\) với C = 10. Tính \(F\), ta được kết quả:
Cho $\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng \(\frac{1}{2}\) thì tỉ số hai đường cao tương ứng là:
Cho tam giác ABC đồng dạng với tam giác DEF theo tỉ số đồng dạng là 2. Tam giác DEF đồng dạng với tam giác MNP theo tỉ số đồng dạng là 2. Biết \(\widehat A = {30^0}\), tính số đo \(\widehat M\)
Tam ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Biết chu vi tam giác MNP là 12cm, chu vi tam giác ABC là:
Cho tam giác ABC vuông tại A, đường cao AH. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng?
(1) \(A{B^2} = BH.CH\)
(2) \(A{C^2} = CH.BC\)
(3) \(B{C^2} = AB.AC\)
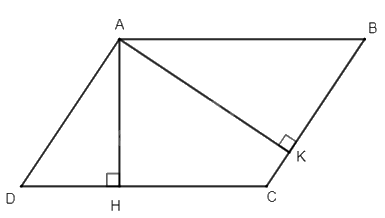
Cho hình bình hành ABCD, kẻ \(AH \bot CD\) tại H; \(AK \bot BC\) tại K. Chọn câu trả lời đúng.
Một mô hình ô tô dài 12cm. Thực tế ô tô dài 2,4m. Tỉ số đồng dạng của mô hình và vật thật là:
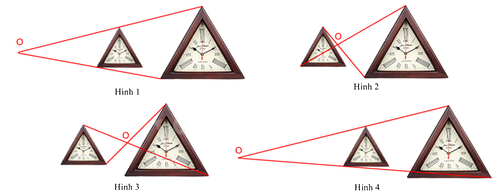
Hình biểu diễn đúng tâm phối cảnh của cặp hình đồng dạng này là:
Giải các phương trình sau:
a) \(x + 2 = - 6x + 16\)
b) \(2\left( {x - 3} \right) = 5\left( {x - 2} \right) + 8\)
c) \(\frac{{x - 1}}{9} + \frac{{x - 3}}{7} = 2\)
d) \(\frac{{2x + 1}}{3} + \frac{{3x - 2}}{2} = \frac{1}{6}\)
Tổ sản xuất được giao dệt một số thảm trong 20 ngày. Nhưng do tổ tăng năng suất 20% nên đã hoàn thành sau 18 ngày. Không những vậy mà tổ còn làm thêm được 24 chiếc thảm. Tính số thảm thực tế tổ sản xuất làm được.
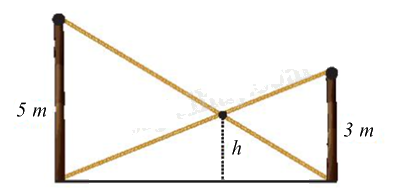
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 5 m và 3 m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm. Tính độ cao ℎ của điểm đó so với mặt đất.
Cho tam giác ABC nhọn (AB < AC) có hai đường cao BE, CF cắt nhau tại H
a) Chứng minh $\Delta ABE\backsim \Delta ACF$
b) Đường thẳng qua E song song với AB, cắt đoạn CH tại D. Chứng minh \(H{E^2} = HD.HC\).
c) Gọi I là trung điểm của CB. Các đường thẳng kẻ từ B song song với CF và từ C song song với BE cắt nhau tại K. Chứng minh H, I, K thẳng hàng.
Cho ba số thực a, b, c khác 2 thỏa mãn a + b + c = 6. Tính giá trị của biểu thức:
\(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}\)
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\).
Phương trình \(3x - y = 0\) là phương trình bậc nhất hai ẩn.
Phương trình \(2y + 1 = 0\) là phương trình bậc nhất ẩn y với \(a = 2\) nên ta chọn đáp án B.
Phương trình \(4 + 0.x = 0\)có a = 0 nên không phải phương trình bậc nhất một ẩn.
Phương trình \(3{x^2} = 8\) là phương trình bậc hai.
Đáp án B.
Phương trình \(3x + m - x - 1 = 0\) nhận \(x = - 3\) là nghiệm thì m là:
Đáp án : C
Thay \(x = - 3\) vào phương trình để tìm m.
Thay \(x = - 3\) vào phương trình \(3x + m - x - 1 = 0\) ta được:
\(\begin{array}{l}3.\left( { - 3} \right) + m - \left( { - 3} \right) - 1 = 0\\ - 9 + m + 3 - 1 = 0\\m - 7 = 0\\m = 7\end{array}\)
Đáp án C.
Một ô tô đi từ A đến B từ 6 giờ sáng, lúc 7 giờ sáng cùng ngày, một xe khách cũng đi từ A và tới B cùng lúc với ô tô. Vậy nếu gọi thời gian đi của xe khách là x ( giờ) thì thời gian đi của ô tô là:
Đáp án : A
Biểu diễn thời gian đi của ô tô theo x.
Vì ô tô đi từ A đến B lúc 6 giờ sáng còn xe khách đi từ A đến B lúc 7 giờ sáng và hai xe đến B cùng lúc nên thời gian ô tô đi từ A đến B là x + (7 – 6) = x + 1 (giờ)
Đáp án A.
Năm nay tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương. Gọi x là tuổi của Phương năm nay vậy thì phương trình tìm x là
Đáp án : A
Biểu diễn các đại lượng qua x.
Tuổi của Phương năm nay là x (tuổi)
Tuổi của mẹ Phương năm nay là 3x (tuổi)
Tuổi của Phương sau 13 năm là x + 13 (tuổi)
Tuổi của mẹ Phương sau 13 năm là 3x + 13 (tuổi)
Vì sau năm tuổi mẹ chỉ còn gấp 2 lần tuổi Phương nên ta có phương trình \(3x + 13 = 2\left( {x + 13} \right)\)
Đáp án A.
Cho công thức \(C = \frac{5}{9}\left( {F - 32} \right)\) với C = 10. Tính \(F\), ta được kết quả:
Đáp án : A
Thay C = 10 để tìm F.
Thay C = 10 vào công thức, ta được:
\(\begin{array}{l}10 = \frac{5}{9}\left( {F - 32} \right)\\18 = F - 32\\F = 18 + 32\\F = 50\end{array}\)
Đáp án A.
Cho $\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng \(\frac{1}{2}\) thì tỉ số hai đường cao tương ứng là:
Đáp án : A
Tỉ số đường cao bằng tỉ số đồng dạng.
Vì $\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng \(\frac{1}{2}\) nên tỉ số hai đường cao tương ứng cũng là \(\frac{1}{2}\).
Đáp án A.
Cho tam giác ABC đồng dạng với tam giác DEF theo tỉ số đồng dạng là 2. Tam giác DEF đồng dạng với tam giác MNP theo tỉ số đồng dạng là 2. Biết \(\widehat A = {30^0}\), tính số đo \(\widehat M\)
Đáp án : A
Chứng minh $\Delta ABC\backsim \Delta MNP$ suy ra số đo góc M.
Vì $\Delta ABC\backsim \Delta DEF$ và $\Delta DEF\backsim \Delta MNP$ suy ra $\Delta ABC\backsim \Delta MNP$ suy ra \(\widehat M = \widehat A = {30^0}\).
Đáp án A.
Tam ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Biết chu vi tam giác MNP là 12cm, chu vi tam giác ABC là:
Đáp án : B
Dựa vào hệ số tỉ lệ của hai tam giác để tính chu vi tam giác ABC.
Vì M, N, P lần lượt là trung điểm của AB, BC, CA nên $\Delta ABC\backsim \Delta MNP$ theo hệ số tỉ lệ là 2.
Do đó \({C_{\Delta ABC}} = 2{C_{\Delta MNP}} = 2.12 = 24\left( {cm} \right)\).
Đáp án B.
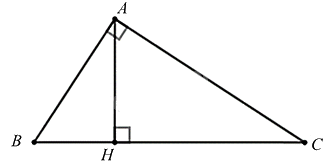
Cho tam giác ABC vuông tại A, đường cao AH. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng?
(1) \(A{B^2} = BH.CH\)
(2) \(A{C^2} = CH.BC\)
(3) \(B{C^2} = AB.AC\)
Đáp án : B
Xác định các tam giác đồng dạng suy ra tỉ số đồng dạng giữa các cạnh.
Ta có:
$\Delta ABC\backsim \Delta HBA\left( g.g \right)\Rightarrow \frac{AB}{BC}=\frac{BH}{AB}\Rightarrow A{{B}^{2}}=BH.BC$ nên khẳng định (1) sai.
$\Delta ABC\backsim \Delta HAC\left( g.g \right)\Rightarrow \frac{AC}{BC}=\frac{CH}{AC}\Rightarrow A{{C}^{2}}=CH.BC$ nên khẳng định (2) đúng.
Khẳng định (3) sai.
Vậy chỉ có 1 khẳng định đúng (khẳng định (2)).
Đáp án B.
Cho hình bình hành ABCD, kẻ \(AH \bot CD\) tại H; \(AK \bot BC\) tại K. Chọn câu trả lời đúng.
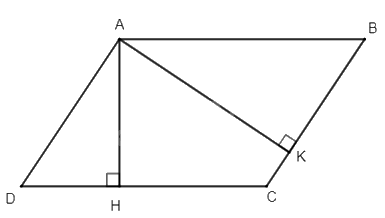
Đáp án : C
Dựa vào tính chất của hình bình hành và các trường hợp đồng dạng của hai tam giác vuông để xác định.
Hình bình hành ABCD có \(\widehat B = \widehat D\)
Xét \(\Delta AHD\) và \(\Delta AKB\) có:
\(\widehat H = \widehat K\left( { = {{90}^0}} \right)\)
\(\widehat B = \widehat D\)
suy ra \(\Delta AHD\backsim \Delta AKB\left( gg \right)\)
Các đỉnh tương ứng là: 2 đỉnh A, đỉnh D và đỉnh B, đỉnh H và đỉnh K nên đáp án C đúng.
Đáp án C.
Một mô hình ô tô dài 12cm. Thực tế ô tô dài 2,4m. Tỉ số đồng dạng của mô hình và vật thật là:
Đáp án : A
Tỉ số đồng dạng của mô hình và vật thật bằng tỉ số giữa độ dài của mô hình với vật thật.
Ta có: 2,4m = 240 cm
Vậy tỉ số đồng dạng của mô hình và vật thật là: \(\frac{{12}}{{240}} = \frac{1}{{20}}\).
Đáp án A.
Hình biểu diễn đúng tâm phối cảnh của cặp hình đồng dạng này là:
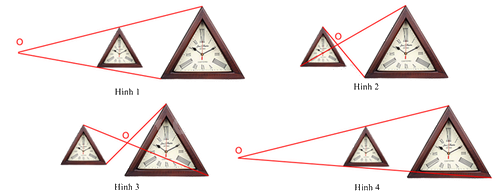
Đáp án : A
Xác định đúng các đỉnh của hai hình để nối được tâm phối cảnh của hai hình bên.
Trong các hình trên, chỉ có hình 1 biểu diễn đúng tâm phối cảnh của cặp hình đồng dạng này.
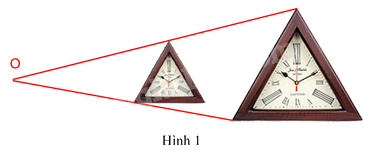
Đáp án A.
Giải các phương trình sau:
a) \(x + 2 = - 6x + 16\)
b) \(2\left( {x - 3} \right) = 5\left( {x - 2} \right) + 8\)
c) \(\frac{{x - 1}}{9} + \frac{{x - 3}}{7} = 2\)
d) \(\frac{{2x + 1}}{3} + \frac{{3x - 2}}{2} = \frac{1}{6}\)
a, b) Đưa phương trình về dạng \(ax + b = 0\) để giải.
c, d) Quy đồng bỏ mẫu đưa phương trình về dạng \(ax + b = 0\) để giải.
a) \(x + 2 = - 6x + 16\)
\(\begin{array}{l}x + 6x = 16 - 2\\7x = 14\\x = 2\end{array}\)
Vậy \(x = 2\)
b) \(2\left( {x - 3} \right) = 5\left( {x - 2} \right) + 8\)
\(\begin{array}{l}2x - 6 = 5x - 10 + 8\\2x - 6 = 5x - 2\\2x - 5x = - 2 + 6\\ - 3x = 4\\x = - \frac{4}{3}\end{array}\)
Vậy \(x = - \frac{4}{3}\)
c) \(\frac{{x - 1}}{9} + \frac{{x - 3}}{7} = 2\)
\(\begin{array}{l}\frac{{7\left( {x - 1} \right)}}{{63}} + \frac{{9\left( {x - 3} \right)}}{{63}} = \frac{{2.63}}{{63}}\\7\left( {x - 1} \right) + 9\left( {x - 3} \right) = 2.63\\7x - 7 + 9x - 27 = 126\\7x + 9x = 126 + 27 + 7\\16x = 160\\x = 10\end{array}\)
Vậy \(x = 10\)
d) \(\frac{{2x + 1}}{3} + \frac{{3x - 2}}{2} = \frac{1}{6}\)
\(\begin{array}{l}\frac{{2\left( {2x + 1} \right)}}{6} + \frac{{3\left( {3x - 2} \right)}}{6} = \frac{1}{6}\\2\left( {2x + 1} \right) + 3\left( {3x - 2} \right) = 1\\4x + 2 + 9x - 6 = 1\\13x = 1 + 6 - 2\\13x = 5\\x = \frac{5}{{13}}\end{array}\)
Vậy \(x = \frac{5}{{13}}\)
Tổ sản xuất được giao dệt một số thảm trong 20 ngày. Nhưng do tổ tăng năng suất 20% nên đã hoàn thành sau 18 ngày. Không những vậy mà tổ còn làm thêm được 24 chiếc thảm. Tính số thảm thực tế tổ sản xuất làm được.
Giải bài toán bằng cách lập phương trình.
Gọi năng suất dự kiến của tổ sản suất là x (chiếc thảm) (\(x \in N*\)).
Biểu diễn năng suất thực tế và số thảm làm được theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi năng suất của tổ sản suất là x (chiếc thảm) (\(x \in N*\)).
Khi đó năng suất thực tế của tổ là: \(x + 20\% x = 120\% x = 1,2x\)
Số thảm tổ cần dệt là: 20x (chiếc thảm)
Số thảm tổ làm được là: \(18.1,2x = 21,6x\).
Vì tổ còn làm thêm được 24 chiếc thảm so với số thảm được giao nên ta có phương trình:
\(20x + 24 = 21,6x\)
Giải phương trình ta được \(x = 15\)(TM)
Vậy số thảm thực tế tổ sản xuất làm được là: \(21,6.15 = 324\) chiếc thảm.
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 5 m và 3 m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm. Tính độ cao ℎ của điểm đó so với mặt đất.
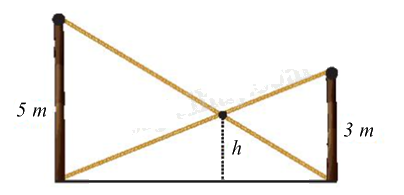
- Theo đề bài vẽ lại hình và đặt tên các điểm.
- Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để tính độ cao của h.
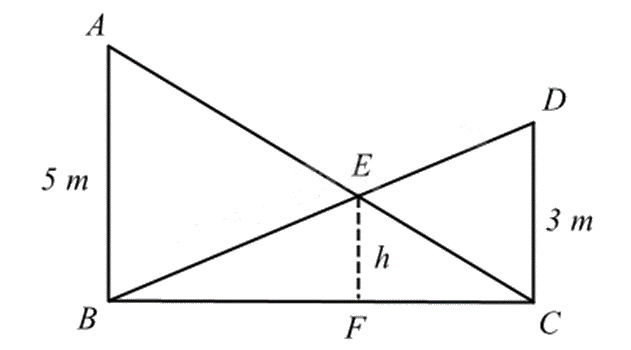
Ta có: AB // CD nên \(\widehat {BAC} = \widehat {DCA}\) và \(\widehat {ABD} = \widehat {CDB}\) (hai góc so le trong)
Xét \(\Delta ABE\) và \(\Delta CDE\) có:
\(\begin{array}{l}\widehat {BAC} = \widehat {DCA}\\\widehat {ABD} = \widehat {CDB}\end{array}\)
Suy ra $\Delta ABE\backsim \Delta CDE$ (gg)
Suy ra \(\frac{{CE}}{{AE}} = \frac{{CD}}{{AB}} = \frac{3}{5}\)
Suy ra \(\frac{{CE}}{{AC}} = \frac{3}{8}\)
Xét \(\Delta CFE\) và \(\Delta CBA\) có:
\(\widehat C\) chung
\(\widehat {ABC} = \widehat {EFC}\)
suy ra $\Delta CFE\backsim \Delta CBA$ (g.g)
suy ra \(\frac{{EF}}{{AB}} = \frac{{CE}}{{AC}} = \frac{3}{8}\). Do đó \(EF = \frac{3}{8}.AB = \frac{3}{8}.5 = \frac{{15}}{8}\) (m)
Cho tam giác ABC nhọn (AB < AC) có hai đường cao BE, CF cắt nhau tại H
a) Chứng minh $\Delta ABE\backsim \Delta ACF$
b) Đường thẳng qua E song song với AB, cắt đoạn CH tại D. Chứng minh \(H{E^2} = HD.HC\).
c) Gọi I là trung điểm của CB. Các đường thẳng kẻ từ B song song với CF và từ C song song với BE cắt nhau tại K. Chứng minh H, I, K thẳng hàng.
a) Chứng minh $\Delta ABE\backsim \Delta ACF$ theo trường hợp góc – góc.
b) Chứng minh $\Delta HED\backsim \Delta HCE$ suy ra tỉ số đồng dạng, ta được điều phải chứng minh.
c) Chứng minh BHCK là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường. Mà I là trung diểm của BC nên I là trung điểm của HK hay H, I, K thẳng hàng.
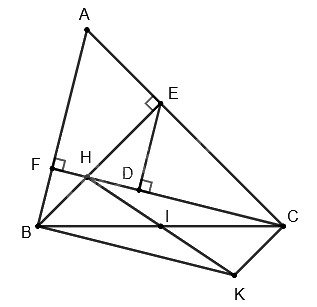
a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat {BEA} = \widehat {CFA} = {90^0}\)
\(\widehat A\) chung
suy ra $\Delta ABE\backsim \Delta ACF$ (g.g) (đpcm)
b) Ta có DE // AB nên \(\widehat {HED} = \widehat {ABE}\) (hai góc so le trong)
\(\widehat {ACF} = \widehat {ABE}\) (do $\Delta ABE\backsim \Delta ACF$)
suy ra \(\widehat {ACF} = \widehat {HED}\)
Xét \(\Delta HED\) và \(\Delta HCE\) có:
\(\widehat H\) chung
\(\widehat {ACF} = \widehat {HED}\)
suy ra $\Delta HED\backsim \Delta HCE$ (g.g)
suy ra \(\frac{{HE}}{{HC}} = \frac{{HD}}{{HE}}\) hay \(H{E^2} = HD.HC\) (đpcm)
c) Xét tứ giác BHCK có:
BH // CK (gt)
BK // HC (gt)
suy ra BHCK là hình bình hành.
Suy ra BC và HK cắt nhau tại trung điểm của mỗi đường.
Mà I là trung điểm của BC nên I cũng là trung điểm của HK hay H, I, K thẳng hàng (đpcm).
Cho ba số thực a, b, c khác 2 thỏa mãn a + b + c = 6. Tính giá trị của biểu thức:
\(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}\)
Quy đồng mẫu các phân thức của biểu thức M.
Đặt a – 2 = x, b – 2 = y, c – 2 = z.
Thay vào M ta được \(M = \frac{{{x^3} + {y^3} + {z^3}}}{{xyz}}\).
Từ a + b + c = 6 suy ra x + y + z = 0
Biến đổi để tính M.
Ta có: \(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}\)
\( = \frac{{{{\left( {a - 2} \right)}^3} + {{\left( {b - 2} \right)}^3} + {{\left( {c - 2} \right)}^3}}}{{\left( {a - 2} \right)\left( {b - 2} \right)\left( {c - 2} \right)}}\)
Đặt a – 2 = x, b – 2 = y, c – 2 = z, biểu thức \(M\) trở thành:
\(M = \frac{{{x^3} + {y^3} + {z^3}}}{{xyz}}\)
Mặt khác, từ a + b + c = 6 suy ra \(\left( {a - 2} \right) + \left( {b - 2} \right) + \left( {c - 2} \right) = 0\) hay \(x + y + z = 0\).
Suy ra
\(\begin{array}{l}x + y = - z\\{\left( {x + y} \right)^3} = {\left( { - z} \right)^3}\\{x^3} + {y^3} + 3xy\left( {x + y} \right) = - {z^3}\\{x^3} + {y^3} + 3xy\left( { - z} \right) = - {z^3}\\{x^3} + {y^3} + {z^3} = 3xyz\end{array}\)
Thay vào M ta được:
\(M = \frac{{3xyz}}{{xyz}} = 3\)
Vậy \(M = 3\).
Kỳ thi học kì 2 Toán 8 đóng vai trò quan trọng trong việc đánh giá kết quả học tập của học sinh trong suốt một học kỳ. Để giúp các em học sinh ôn tập và tự tin bước vào kỳ thi, giaitoan.edu.vn cung cấp Đề thi học kì 2 Toán 8 - Đề số 2 - Cánh diều với đầy đủ các dạng bài tập và đáp án chi tiết.
Đề thi học kì 2 Toán 8 - Đề số 2 - Cánh diều bao gồm các nội dung chính sau:
Để giải các bài tập về đa thức, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia đa thức. Đồng thời, cần biết cách phân tích đa thức thành nhân tử để đơn giản hóa biểu thức và giải phương trình.
Ví dụ: Phân tích đa thức x2 - 4 thành nhân tử.
Giải:x2 - 4 = (x - 2)(x + 2)
Các bài tập về hình học thường yêu cầu học sinh chứng minh các tính chất của hình, tính diện tích, chu vi, góc. Để giải các bài tập này, học sinh cần nắm vững các định lý, tính chất và công thức liên quan.
Ví dụ: Cho hình chữ nhật ABCD, gọi O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB = OC = OD.
Giải: Vì ABCD là hình chữ nhật nên hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm O. Do đó, OA = OC = 1/2AC và OB = OD = 1/2BD. Suy ra OA = OB = OC = OD.
Các bài tập về hàm số thường yêu cầu học sinh vẽ đồ thị hàm số, tìm tọa độ giao điểm, giải phương trình hàm số. Để giải các bài tập này, học sinh cần nắm vững các khái niệm về hàm số, đồ thị hàm số và các phương pháp giải phương trình.
Ví dụ: Vẽ đồ thị hàm số y = 2x + 1.
Giải: Đồ thị hàm số y = 2x + 1 là một đường thẳng cắt trục Oy tại điểm (0, 1) và có hệ số góc là 2.
Đề thi học kì 2 Toán 8 - Đề số 2 - Cánh diều là một tài liệu ôn tập hữu ích cho học sinh. Hy vọng rằng với đề thi này, các em sẽ có thêm công cụ để chuẩn bị tốt nhất cho kỳ thi sắp tới và đạt được kết quả cao nhất.