Giaitoan.edu.vn xin giới thiệu Đề thi học kì 2 Toán 8 - Đề số 3 - Cánh diều, một công cụ hỗ trợ học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 8, tập trung vào các kiến thức trọng tâm và có đáp án chi tiết để học sinh tự kiểm tra.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và áp dụng kiến thức vào thực tế.
Trong các phương trình sau, phương trình bậc nhất một ẩn là
Phương trình nào sau đây nhận \(m = 2\) là nghiệm?
Phương trình \(x + 5 = x + 5\) có
Năm nay tuổi cha 39 tuổi và gấp 3 lần tuổi con năm ngoái. Vậy năm nay tuổi con là
Tiền lương cơ bản của An mỗi tháng là x (triệu đồng). Tiền phụ cấp mỗi tháng là 2 000 000 (đồng). Biểu thức biểu thị tiền lương mỗi tháng của An (bằng tổng tiền lương cơ bản và tiền phụ cấp; đơn vị là triệu đồng) là:
Cho $\Delta ABC\backsim \Delta DEF$ biết AB = 4 cm; AC = 6 cm; BC = 10 cm và DE = 2 cm khi đó tỉ số đồng dạng bằng
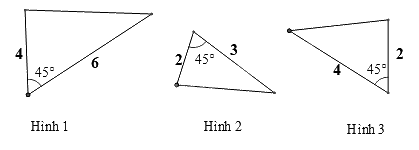
Hãy chỉ ra cặp tam giác đồng dạng trong các tam giác sau
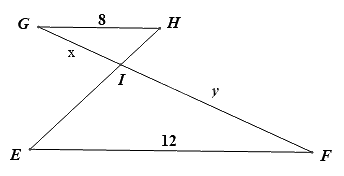
Cho $\Delta GHI\backsim \Delta FEI$ có các kính thước như hình vẽ, khi đó tỉ số độ dài của y và x bằng:
Cho hình vẽ
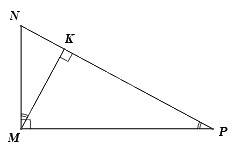
Khi đó các khẳng định sau
(1) $\Delta MKN\backsim \Delta PKM\text{ (g}\text{.g)}$.
(2) $\Delta MKP\backsim \Delta MNP\text{ (g}\text{.g)}$.
Hãy chọn đáp án đúng:
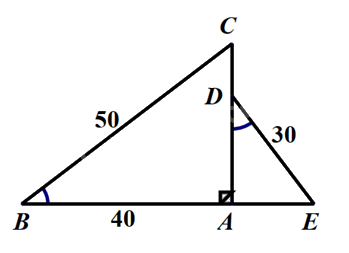
Cho hình vẽ sau, biết \(\widehat B = \widehat D,BC = 50cm,AB = 40cm,DE = 30cm\). Độ dài đoạn thẳng AD là:
Trong các hình đã học cặp hình nào sau đây luôn đồng dạng?
Trong hình dưới đây, hình b là hình a sau khi phóng to với kích thước k = 2. Nếu kích thước của hình a là 3 x 4 thì kích thước của hình b là:

Giải các phương trình sau:
a) \(2x - 4 = 3x + 1\)
b) \(7\left( {5 - x} \right) = 11 - 5x\)
c) \(\frac{5}{6} + \frac{x}{4} = 2 - \frac{x}{3}\)
d) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{{1 + 3x}}{4} + \frac{1}{2}\)
Giải bài toán bằng cách lập phương trình
Có hai loại dung dịch muối I và II. Người ta hòa 200 gam dung dịch muối I với 300 gam dung dịch muối II thì được một dung dịch có nồng độ muối là 33%. Tính nồng độ muối trong dung dịch I và II, biết rằng nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20%.
Cho \(\Delta ABC\) vuông tại A có \(AB = 6cm\) và \(AC = 8cm\). Đường phân giác của góc ABC cắt AC tại D. Từ C kẻ \(CE \bot BD\) kẻ E.
a) Tính độ dài BC và tỉ số \(\frac{{AD}}{{DC}}\).
b) Chứng minh $\Delta ABD\backsim \Delta EBC$. Từ đó suy ra \(BD.EC = AD.BC\).
c) Chứng minh \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}\).
d) Gọi EH là đường cao của \(\Delta EBC\). Chứng minh \(CH.CB = ED.EB\).
Chu vi của một mảnh vườn hình chữ nhật là 42 m. Biết chiều rộng ngắn hơn chiều dài 3 m. Tìm chiều dài của mảnh vườn.
Cho \({a_1};{a_2};...;{a_{2024}}\) là 2024 số thực thỏa mãn \({a_k} = \frac{{2k + 1}}{{{{\left( {{k^2} + k} \right)}^2}}}\) với \(k \in \left\{ {1;2;...;2024} \right\}\).
Tính tổng \({S_{2024}} = {a_1} + {a_2} + {a_3} + ... + {a_{2024}}\).
Trong các phương trình sau, phương trình bậc nhất một ẩn là
Đáp án : A
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\).
Phương trình bậc nhất một ẩn là phương trình \(2x + 1 = 0\).
Đáp án A.
Phương trình nào sau đây nhận \(m = 2\) là nghiệm?
Đáp án : A
Thay m = 2 vào phương trình để xác định.
Ta có: 2 – 2 = 0 nên phương trình m – 2 nhận m = 2 là nghiệm.
Đáp án A.
Phương trình \(x + 5 = x + 5\) có
Đáp án : A
Giải phương trình để tìm nghiệm.
\(\begin{array}{l}x + 5 = x + 5\\x - x = 5 - 5\end{array}\)
\(0 = 0\) (luôn đúng)
Vậy phương trình \(x + 5 = x + 5\) có vô số nghiệm.
Đáp án A.
Năm nay tuổi cha 39 tuổi và gấp 3 lần tuổi con năm ngoái. Vậy năm nay tuổi con là
Đáp án : C
Gọi tuổi con hiện tại là x.
Lập phương trình.
Giải phương trình để tìm tuổi con. Kiểm tra kết quả.
Gọi tuổi của con hiện tại là x \(\left( {x > 1,x \in N*} \right)\)
Vì năm nay cha 39 tuổi và gấp 3 lần tuổi con năm ngoái nên ta có phương trình:
\(\begin{array}{l}3\left( {x - 1} \right) = 39\\x - 1 = 13\\x = 14(TM)\end{array}\)
Vậy năm nay con 14 tuổi.
Đáp án C.
Tiền lương cơ bản của An mỗi tháng là x (triệu đồng). Tiền phụ cấp mỗi tháng là 2 000 000 (đồng). Biểu thức biểu thị tiền lương mỗi tháng của An (bằng tổng tiền lương cơ bản và tiền phụ cấp; đơn vị là triệu đồng) là:
Đáp án : D
Biểu diễn tiền lương mỗi tháng theo x.
Vì tiền lương mỗi tháng của An bằng tổng tiền lương cơ bản và tiền phụ cấp nên ta có biểu thức:
\(x + 2\) (triệu đồng)
Đáp án D.
Cho $\Delta ABC\backsim \Delta DEF$ biết AB = 4 cm; AC = 6 cm; BC = 10 cm và DE = 2 cm khi đó tỉ số đồng dạng bằng
Đáp án : B
Dựa vào tam giác đồng dạng suy ra tỉ số dựa vào tỉ số các cạnh tương ứng.
Vì $\Delta ABC\backsim \Delta DEF$ nên tỉ số đồng dạng là: \(k = \frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\) hay \(k = \frac{{AB}}{{DE}} = \frac{4}{2} = 2\).
Đáp án B.
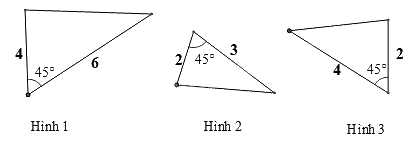
Hãy chỉ ra cặp tam giác đồng dạng trong các tam giác sau
Đáp án : A
Chứng minh hai tam giác đồng dạng theo trường hợp c.g.c.
Xét hình 1 và hình 2 có một góc \({45^0}\), tỉ số hai cạnh kề góc dó là \(\frac{4}{6} = \frac{2}{3}\) nên hình 1 và hình 2 là hai tam giác đồng dạng.
Xét hình 1 và hình 2 có một góc \({45^0}\), tỉ số hai cạnh kề góc dó là \(\frac{4}{6} = \frac{2}{3} \ne \frac{2}{4}\) nên hình 1 và hình 3 không là hai tam giác đồng dạng.
Từ đó suy ra hình 2 và hình 3 cũng không đồng dạng.
Vậy A đúng.
Đáp án A.
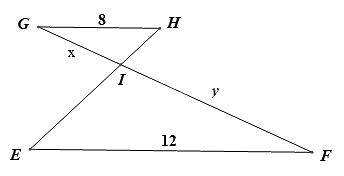
Cho $\Delta GHI\backsim \Delta FEI$ có các kính thước như hình vẽ, khi đó tỉ số độ dài của y và x bằng:
Đáp án : C
Từ hai tam giác đồng dạng suy ra tỉ số đồng dạng
Vì $\Delta GHI\backsim \Delta FEI$ nên \(\frac{y}{x} = \frac{{IF}}{{GI}} = \frac{{EF}}{{GH}} = \frac{{12}}{8} = \frac{3}{2}\).
Đáp án C.
Cho hình vẽ

Khi đó các khẳng định sau
(1) $\Delta MKN\backsim \Delta PKM\text{ (g}\text{.g)}$.
(2) $\Delta MKP\backsim \Delta MNP\text{ (g}\text{.g)}$.
Hãy chọn đáp án đúng:
Đáp án : A
Xác định xem \(\Delta MKN\backsim \Delta PKM\) và $\Delta MKP\backsim \Delta MNP$ có đúng hay không.
\(\Delta MKN\) và \(\Delta PKM\) có \(\widehat N\) chung, \(\widehat M = \widehat K = {90^0}\) nên \(\Delta MKN\backsim \Delta PKM\) (g.g) suy ra khẳng định (1) đúng.
Tương tự $\Delta MKP\backsim \Delta NMP$ (g.g). Khẳng định (2) không đúng vì các đỉnh của hai tam giác đồng dạng chưa được viết chính xác.
Vậy chỉ có khẳng định (1) đúng.
Đáp án A.
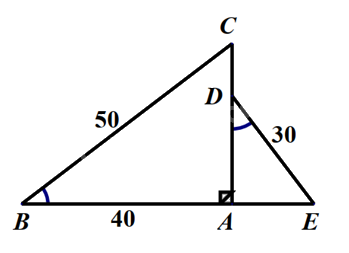
Cho hình vẽ sau, biết \(\widehat B = \widehat D,BC = 50cm,AB = 40cm,DE = 30cm\). Độ dài đoạn thẳng AD là:
Đáp án : B
Chứng minh $\Delta ABC\backsim \Delta ADE$ suy ra tỉ số giữa các cạnh tương ứng.
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
\(\widehat B = \widehat D\)
\(\widehat {CAB} = \widehat {EAD}\left( { = {{90}^0}} \right)\)
Suy ra $\Delta ABC\backsim \Delta ADE$ (g.g) suy ra \(\frac{{AB}}{{BC}} = \frac{{AD}}{{DE}}\) hay \(\frac{{40}}{{50}} = \frac{{AD}}{{30}}\) suy ra \(AD = 30.\frac{{40}}{{50}} = 24\)(cm).
Đáp án B.
Trong các hình đã học cặp hình nào sau đây luôn đồng dạng?
Đáp án : D
Dựa vào đặc điểm của các hình để xác định.
Trong các hình trên chỉ có hình vuông là hình có các cạnh bằng nhau, các góc bằng nhau nên luôn đồng dạng.
Đáp án D.
Trong hình dưới đây, hình b là hình a sau khi phóng to với kích thước k = 2. Nếu kích thước của hình a là 3 x 4 thì kích thước của hình b là:

Đáp án : B
Dựa vào tỉ số k tính kích thước cạnh hình b.
Vì hình b là hình a sau khi phóng to với kích thước k = 2 nên cạnh của hình b gấp 2 lần cạnh của hình a.
Ta có: 3.2 = 6; 4.2 = 8
\( \Rightarrow \) Kích thước hình b là 6 x 8.
Đáp án B.
Giải các phương trình sau:
a) \(2x - 4 = 3x + 1\)
b) \(7\left( {5 - x} \right) = 11 - 5x\)
c) \(\frac{5}{6} + \frac{x}{4} = 2 - \frac{x}{3}\)
d) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{{1 + 3x}}{4} + \frac{1}{2}\)
a, b) Đưa phương trình về dạng \(ax + b = 0\) để giải.
c, d) Quy đồng bỏ mẫu đưa phương trình về dạng \(ax + b = 0\) để giải.
a) \(2x - 4 = 3x + 1\)
\(\begin{array}{l}2x - 3x = 1 + 4\\ - x = 5\\x = - 5\end{array}\)
Vậy \(x = - 5\).
b) \(7\left( {5 - x} \right) = 11 - 5x\)
\(\begin{array}{l}35 - 7x = 11 - 5x\\ - 7x + 5x = 11 - 35\\ - 2x = - 24\\x = 12\end{array}\)
Vậy \(x = 12\).
c) \(\frac{5}{6} + \frac{x}{4} = 2 - \frac{x}{3}\)
\(\begin{array}{l}\frac{{10}}{{12}} + \frac{{3x}}{{12}} = \frac{{24}}{{12}} - \frac{{4x}}{{12}}\\10 + 3x = 24 - 4x\\3x + 4x = 24 - 10\\7x = 14\\x = 2\end{array}\)
Vậy \(x = 2\).
d) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{{1 + 3x}}{5} + \frac{1}{2}\)
\(\begin{array}{l}\frac{{10.2\left( {x + 1} \right)}}{{30}} = \frac{{6\left( {1 + 3x} \right)}}{{30}} + \frac{{15}}{{30}}\\20\left( {x + 1} \right) = 6\left( {1 + 3x} \right) + 15\\20x + 20 = 6 + 18x + 15\\20x - 18x = 6 + 15 - 20\\2x = 1\\x = \frac{1}{2}\end{array}\)
Vậy \(x = \frac{1}{2}\).
Giải bài toán bằng cách lập phương trình
Có hai loại dung dịch muối I và II. Người ta hòa 200 gam dung dịch muối I với 300 gam dung dịch muối II thì được một dung dịch có nồng độ muối là 33%. Tính nồng độ muối trong dung dịch I và II, biết rằng nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20%.
Giải bài toán bằng cách lập phương trình.
Gọi nồng độ muối trong dung dịch I là x (%) (x > 0)
Biểu diễn nồng độ muối trong dung dịch II, khối lượng muối trong hai dung dịch theo x và lập phương trình (Sử dụng công thức \(C\% = \frac{{{m_{ct}}.100\% }}{{{m_{hh}}}}\)).
Giải phương trình và kiểm tra nghiệm.
Gọi nồng độ muối trong dung dịch I là \(x\left( \% \right)\left( {x > 0} \right)\).
Khi đó khối lượng muối có trong dung dịch I là:
\(200.x\% = 200\frac{x}{{100}} = 2x\)(g).
Do nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20% nên nồng độ muối trong dung dịch II là \(x - 20\left( \% \right)\)
Khi đó khối lượng muối có trong dung dịch II là:
\(300.\left( {x - 20} \right)\% = 300.\frac{{x - 20}}{{100}} = 3\left( {x - 20} \right)\)(g).
Khối lượng muối trong dung dịch sau khi trộn hai dung dịch là:
\(2x + 3\left( {x - 20} \right)\)(g).
Khối lượng dung dịch muối sau khi trộn hai dung dịch là: \(200 + 300 = 500\)(g).
Do sau khi trộn hai dung dịch I và II thì được một dung dịch có nồng độ muối là 33% nên ta có phương trình: \(\frac{{2x + 3\left( {x - 20} \right)}}{{500}}.100\% = 33\% \) hay \(2x + 3\left( {x - 20} \right) = 165\)
Giải phương trình ta được \(x = 45\)(thỏa mãn).
Suy ra nồng độ muối trong dung dịch II là: \(40 - 20 = 25\left( \% \right)\)
Vậy nồng độ muối của dung dịch I và II lần lượt là 45% và 25%.
Cho \(\Delta ABC\) vuông tại A có \(AB = 6cm\) và \(AC = 8cm\). Đường phân giác của góc ABC cắt AC tại D. Từ C kẻ \(CE \bot BD\) kẻ E.
a) Tính độ dài BC và tỉ số \(\frac{{AD}}{{DC}}\).
b) Chứng minh $\Delta ABD\backsim \Delta EBC$. Từ đó suy ra \(BD.EC = AD.BC\).
c) Chứng minh \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}\).
d) Gọi EH là đường cao của \(\Delta EBC\). Chứng minh \(CH.CB = ED.EB\).
a) Sử dụng định lí Pythagore để tính BC, sử dụng tính chất tia phân giác để tính \(\frac{{AD}}{{DC}}\).
b) Chứng minh $\Delta ABD\backsim \Delta EBC$ theo trường hợp góc – góc suy ra tỉ số các cạnh tương ứng.
c) Chứng minh \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}} = \frac{{AD}}{{AB}}\)
d) Chứng minh \(CH.CB = ED.EB = C{E^2}\)
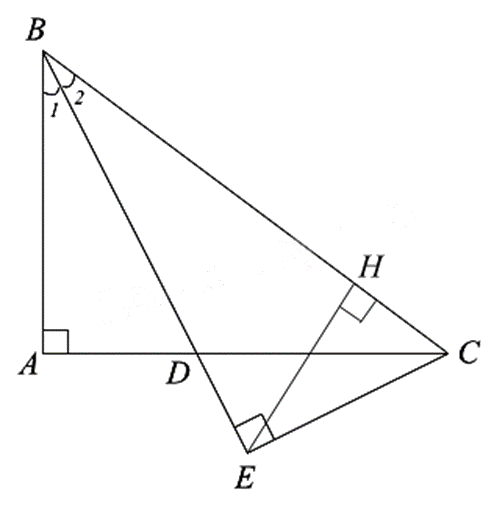
a) Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông tại A, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\)
Suy ra \(BC = \sqrt {100} = 10\) (cm).
Vì BD là tia phân giác của góc ABC nên ta có:
\(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\)
b) Theo đề bài, \(CE \bot BD\) tại E nên \(\widehat {BEC} = {90^0}\)
Xét \(\Delta ABD\) và \(\Delta EBC\) có:
\(\widehat {BAD} = \widehat {BEC} = {90^0}\)
\(\widehat {{B_1}} = \widehat {{B_2}}\) (BD là tia phân giác của góc ABC)
Suy ra $\Delta ABD\backsim \Delta EBC$ (g.g) (đpcm)
Suy ra \(\frac{{BD}}{{AD}} = \frac{{BC}}{{EC}}\) (tỉ số các cạnh tương ứng)
Do đó \(BD.EC = AD.BC\) (đpcm)
c) Vì \(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}}\) nên \(\frac{{CD}}{{BC}} = \frac{{AD}}{{AB}}\) (1)
Vì $\Delta ABD\backsim \Delta EBC$ (cmt) nên \(\frac{{AD}}{{EC}} = \frac{{AB}}{{EB}}\) suy ra \(\frac{{AD}}{{AB}} = \frac{{EC}}{{EB}}\) (2)
Từ (1) và (2) suy ra \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}\) (đpcm)
d) Xét \(\Delta CHE\) và \(\Delta CEB\) có:
\(\widehat {CHE} = \widehat {CEB} = {90^0}\)
\(\widehat C\) chung
Suy ra $\Delta CHE\backsim \Delta CEB$ (g.g) nên \(\frac{{CH}}{{CE}} = \frac{{CE}}{{CB}}\) suy ra \(CH.CB = C{E^2}\) (3)
Tương tự, $\Delta CDE\backsim \Delta BCE$ (g.g) nên \(\frac{{ED}}{{EC}} = \frac{{CE}}{{BE}}\) suy ra \(ED.EB = C{E^2}\)(4)
Từ (3) và (4) suy ra \(CH.CB = ED.EB\) (đpcm)
Chu vi của một mảnh vườn hình chữ nhật là 42 m. Biết chiều rộng ngắn hơn chiều dài 3 m. Tìm chiều dài của mảnh vườn.
Gọi chiều dài của mảnh vườn là x.
Biểu thị chiều rộng mảnh vườn theo x và giải phương trình.
Gọi chiều dài của mảnh vườn là x (m), x > 3.
Chiều rộng của mảnh vườn là: x – 3 (m)
Vì chu vi của mảnh vườn hình chữ nhật là 42m nên ta có phương trình:
\(\begin{array}{l}2\left[ {x + \left( {x - 3} \right)} \right] = 42\\2x - 3 = 21\\2x = 24\\x = 12\left( {TM} \right)\end{array}\)
Vậy chiều dài của mảnh vườn là 12 m.
Cho \({a_1};{a_2};...;{a_{2024}}\) là 2024 số thực thỏa mãn \({a_k} = \frac{{2k + 1}}{{{{\left( {{k^2} + k} \right)}^2}}}\) với \(k \in \left\{ {1;2;...;2024} \right\}\).
Tính tổng \({S_{2024}} = {a_1} + {a_2} + {a_3} + ... + {a_{2024}}\).
Phân tích \({a_k} = \frac{{2k + 1}}{{{{\left( {{k^2} + k} \right)}^2}}} = \frac{1}{{{k^2}}} - \frac{1}{{{{\left( {k + 1} \right)}^2}}}\)
Từ đó tính \({S_{2024}}\).
Ta có:
\({a_k} = \frac{{2k + 1}}{{{{\left( {{k^2} + k} \right)}^2}}} = \frac{{2k + 1}}{{{{\left[ {k\left( {k + 1} \right)} \right]}^2}}} = \frac{{{{\left( {k + 1} \right)}^2} - {k^2}}}{{{k^2}{{\left( {k + 1} \right)}^2}}} = \frac{1}{{{k^2}}} - \frac{1}{{{{\left( {k + 1} \right)}^2}}}\)
Do đó:
\(\begin{array}{l}{S_{2024}} = {a_1} + {a_2} + {a_3} + ... + {a_{2024}}\\ = \left( {\frac{1}{{{1^2}}} - \frac{1}{{{2^2}}}} \right) + \left( {\frac{1}{{{2^2}}} - \frac{1}{{{3^2}}}} \right) + \left( {\frac{1}{{{3^2}}} - \frac{1}{{{4^2}}}} \right) + ... + \left( {\frac{1}{{{{2023}^2}}} - \frac{1}{{{{2024}^2}}}} \right)\\ = 1 - \frac{1}{{{{2024}^2}}}\\ = \frac{{{{2024}^2} - 1}}{{{{2024}^2}}}\end{array}\)
Vậy \({S_{2024}} = \frac{{{{2024}^2} - 1}}{{{{2024}^2}}}\)
Kỳ thi học kì 2 Toán 8 đóng vai trò quan trọng trong việc đánh giá kết quả học tập của học sinh trong suốt một học kỳ. Để giúp các em học sinh ôn tập và tự tin bước vào kỳ thi, giaitoan.edu.vn cung cấp Đề thi học kì 2 Toán 8 - Đề số 3 - Cánh diều với đầy đủ các dạng bài tập và đáp án chi tiết.
Đề thi được cấu trúc theo chương trình học Toán 8, bao gồm các chủ đề chính sau:
Trong đề thi, các em học sinh thường gặp các dạng bài tập sau:
Giaitoan.edu.vn cung cấp đáp án chi tiết cho từng câu hỏi trong đề thi, giúp học sinh hiểu rõ phương pháp giải và tự kiểm tra kết quả của mình. Các lời giải được trình bày một cách dễ hiểu, logic và có ví dụ minh họa.
Để đạt kết quả tốt nhất trong kỳ thi học kì 2 Toán 8, các em học sinh nên lưu ý những mẹo sau:
Ngoài Đề thi học kì 2 Toán 8 - Đề số 3 - Cánh diều, giaitoan.edu.vn còn cung cấp nhiều tài liệu ôn tập bổ sung khác, như:
Đề thi học kì 2 Toán 8 - Đề số 3 - Cánh diều là một công cụ hữu ích giúp học sinh ôn tập và chuẩn bị tốt nhất cho kỳ thi. Hãy luyện tập thường xuyên và áp dụng những mẹo làm bài thi hiệu quả để đạt kết quả cao nhất!