Giaitoan.edu.vn xin giới thiệu Đề thi học kì 2 Toán 8 - Đề số 1 - Cánh diều, một tài liệu ôn tập vô cùng quan trọng dành cho học sinh lớp 8. Đề thi này được biên soạn theo chương trình sách giáo khoa Cánh diều, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Với đề thi này, các em có thể tự đánh giá năng lực của mình, xác định những kiến thức còn yếu và tập trung ôn tập để đạt kết quả tốt nhất trong kỳ thi sắp tới.
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Với \(m = - 1\) thì phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\)
Phương trình \(4x - 2 = 0\) có nghiệm là
Nếu một vòi nước chảy đầy bể trong 5 giờ thì 1 giờ vòi nước đó chảy được bao nhiêu phần bể?
Một tam giác có độ dài các cạnh là \(x + 3\); \(x + 1\); \(x + 5\). Biểu thức biểu thị chu vi tam giác đó là
Năm nay chị 27 tuổi và tuổi em ít hơn tuổi chị 5 tuổi. Vậy năm sau tuổi em là
Hãy chọn câu khẳng định đúng.
$\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng k. Vậy k bằng tỉ số nào sau đây?
Cho hình sau. Biết \(\Delta ABC,\Delta ADE\) là hai tam giác cân.
Chọn kết luận đúng trong các câu sau:
Cho hình vẽ sau. Độ lớn x bằng bao nhiêu để hai tam giác đồng dạng?
Cho hình dưới đây. Biết AB // DE. Chọn hệ thức sai trong các câu sau:
Cặp hình đồng dạng trong hình dưới đây là:
Giải các phương trình sau:
a) \(\frac{2}{3}x + 2\frac{1}{2} = 0\)
b) \(4 - 3x = 5\)
c) \(\frac{{7x - 1}}{6} = \frac{{16 - x}}{5} - 2x\)
Giải bài toán bằng cách lập phương trình
Một xe tải và một xe con cùng khởi hành từ tỉnh A đến tỉnh B. Xe tải đi với vận tốc 30km/h, xe con đi với vận tốc 45km/h. Sau khi đi được \(\frac{3}{4}\) quãng đường AB, xe con tăng vận tốc 5km/h trên quãng đường còn lại thì đến B sớm hơn xe tải là 2 giờ 27 phút. Tính quãng đường AB.
Tìm m để phương trình \(2\left( {x - 1} \right) - mx = 3\):
a) Vô nghiệm
b) Có nghiệm duy nhất
Cho \(\Delta ABC\) nhọn có AB < AC. Đường cao AH. Qua H vẽ \(HM \bot AB\) và \(HN \bot AC\).
a) Chứng minh $\Delta AMH\backsim \Delta AHB$.
b) Chứng minh \(AN.AC = A{H^2}\).
c) Vẽ đường cao BD cắt AH tại E. Qua D vẽ đường thẳng song song với MN cắt AB tại F. Chứng minh \(\widehat {AEF} = \widehat {ABC}\).
Giải phương trình:
\(\left( {\frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}} \right)x = \left( {\frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}} \right)\)
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\).
Phương trình \(2x - 5 = 0\) có dạng \(ax + b = 0\) với \(a = 2\) nên ta chọn đáp án B.
Đáp án B.
Với \(m = - 1\) thì phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\)
Đáp án : B
Thay m vào phương trình, đưa phương trình về dạng ax + b = 0 để giải.
Thay \(m = - 1\) vào phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\), ta có:
\(\begin{array}{l}\left[ {2{{\left( { - 1} \right)}^2} - 2} \right]x = - 1 + 1\\\left( {2 - 2} \right)x = 0\end{array}\)
\(0.x = 0\) (luôn đúng).
Vậy phương trình có vô số nghiệm.
Đáp án B.
Phương trình \(4x - 2 = 0\) có nghiệm là
Đáp án : D
Giải phương trình có dạng \(ax + b = 0\).
Ta có:
\(\begin{array}{l}4x - 2 = 0\\4x = 2\\x = \frac{1}{2}\end{array}\)
Đáp án D.
Nếu một vòi nước chảy đầy bể trong 5 giờ thì 1 giờ vòi nước đó chảy được bao nhiêu phần bể?
Đáp án : C
Coi bể nước bằng 1. Tính số phần bể mà vòi chảy được trong 1 giờ.
Coi bể nước là 1. Vì vòi nước chảy đầy bể trong 5 giờ nên trong 1 giờ vòi chảy được là:
\(1:5 = \frac{1}{5}\) (bể)
Đáp án C.
Một tam giác có độ dài các cạnh là \(x + 3\); \(x + 1\); \(x + 5\). Biểu thức biểu thị chu vi tam giác đó là
Đáp án : A
Sử dụng công thức tính chu vi tam giác để viết biểu thức.
Biểu thức biểu thị chu vi tam giác đó là:
\(x + 3 + x + 1 + x + 5 = 3x + 9\).
Đáp án A.
Năm nay chị 27 tuổi và tuổi em ít hơn tuổi chị 5 tuổi. Vậy năm sau tuổi em là
Đáp án : C
Gọi tuổi của em là x, biểu thị tuổi của chị theo tuổi của em và tính tuổi em năm sau.
Gọi tuổi của em là x (tuổi), \(x \in N*\).
Vì tuổi em ít hơn tuổi chị 5 tuổi nên x + 5 = 27
Giải phương trình ta được x = 27 – 5 = 22 (tuổi) (TM)
Vậy năm sau tuổi của em là: 22 + 1 = 23 tuổi.
Đáp án C.
Hãy chọn câu khẳng định đúng.
Đáp án : A
Dựa vào kiến thức về hai tam giác đồng dạng.
Hai tam giác bằng nhau thì đồng dạng nên ta chọn đáp án A.
Đáp án A.
$\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng k. Vậy k bằng tỉ số nào sau đây?
Đáp án : B
Xác định tỉ số giữa các cạnh tương ứng của hai tam giác.
$\Delta ABC\backsim \Delta DEF$ nên \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = k\).
Vậy \(k = \frac{{AC}}{{DF}}\).
Đáp án B.
Cho hình sau. Biết \(\Delta ABC,\Delta ADE\) là hai tam giác cân.
Chọn kết luận đúng trong các câu sau:
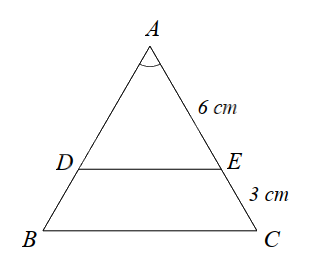
Đáp án : C
Chứng minh $\Delta ADE\backsim \Delta ABC$ theo trường hợp cạnh – góc – cạnh.
Vì \(\Delta ABC,\Delta ADE\) cân nên \(AB = AC\); \(AD = AE\left( { = 6cm} \right)\).
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
\(\widehat A\) chung
\(\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}}\) (vì \(AB = AC;AD = AE\))
suy ra $\Delta ABC\backsim \Delta ADE\left( c.g.c \right)$
suy ra \(k = \frac{{AC}}{{AE}} = \frac{{AE + EC}}{{AE}} = \frac{{6 + 3}}{6} = \frac{9}{6} = \frac{3}{2}\).
Đáp án C.
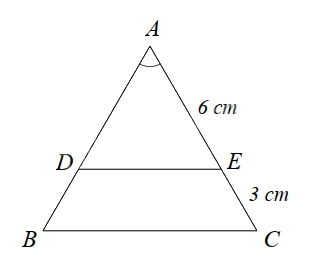
Cho hình vẽ sau. Độ lớn x bằng bao nhiêu để hai tam giác đồng dạng?
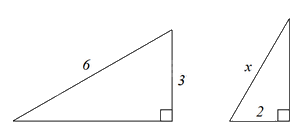
Đáp án : B
Dựa vào các trường hợp đồng dạng của hai tam giác để tìm x.
Để hai tam giác đồng dạng thì \(\frac{2}{3} = \frac{x}{6}\) suy ra \(x = \frac{2}{3}.6 = 4\).
Đáp án B.
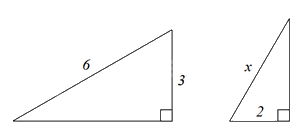
Cho hình dưới đây. Biết AB // DE. Chọn hệ thức sai trong các câu sau:
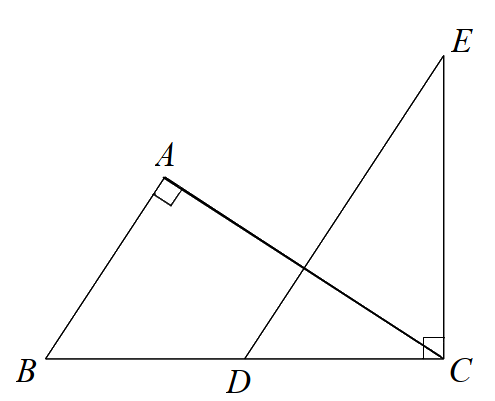
Đáp án : D
Dựa vào AB // DE suy ra \(\widehat {ABC} = \widehat {EDC}\).
Chứng minh $\Delta ABC\backsim \Delta CDE\left( g.g \right)$ suy ra tỉ số giữa các cặp cạnh tương ứng.
Vì AB // DE nên \(\widehat {ABC} = \widehat {EDC}\) (hai góc đồng vị)
Xẻ \(\Delta ABC\) và \(\Delta CDE\) có:
\(\widehat A = \widehat C\left( { = {{90}^0}} \right)\)
\(\widehat {ABC} = \widehat {EDC}\) (cmt)
Suy ra $\Delta ABC\backsim \Delta CDE\left( g.g \right)$. Từ đó ta được:
\(\frac{{AB}}{{AC}} = \frac{{CD}}{{CE}}\) suy ra \(AB.CE = AC.CD\). (A đúng)
\(\frac{{AB}}{{BC}} = \frac{{CD}}{{DE}}\) suy ra \(AB.DE = BC.CD\) (B đúng)
\(\frac{{AC}}{{BC}} = \frac{{CE}}{{DE}}\) suy ra \(AC.DE = CE.BC\) (C đúng)
Vậy D sai (vì không có tỉ lệ nào suy ra \(AB.AC = DE.DC\)).
Đáp án D.
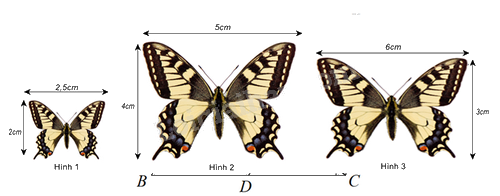
Cặp hình đồng dạng trong hình dưới đây là:
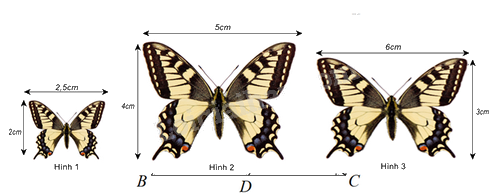
Đáp án : A
Kiểm tra tỉ số các cặp cạnh của các hình trên.
Ta có: \(\frac{2}{{2,5}} = \frac{4}{5} \ne \frac{3}{6}\) nên hình 1 và hình 2 là hai hình đồng dạng
Đáp án A.
Giải các phương trình sau:
a) \(\frac{2}{3}x + 2\frac{1}{2} = 0\)
b) \(4 - 3x = 5\)
c) \(\frac{{7x - 1}}{6} = \frac{{16 - x}}{5} - 2x\)
Đưa phương trình về dạng ax + b = 0 để giải.
a) \(\frac{2}{3}x + 2\frac{1}{2} = 0\)
\(\begin{array}{l}\frac{2}{3}x + \frac{5}{2} = 0\\\frac{2}{3}x = - \frac{5}{2}\\x = - \frac{5}{2}:\frac{2}{3}\\x = - \frac{{15}}{4}\end{array}\)
Vậy nghiệm của phương trình là \(x = - \frac{{15}}{4}\).
b) \(4 - 3x = 5\)
\(\begin{array}{l} - 3x = 5 - 4\\ - 3x = 1\\x = \frac{{ - 1}}{3}\end{array}\)
Vậy nghiệm của phương trình là \(x = \frac{{ - 1}}{3}\).
c) \(\frac{{7x - 1}}{6} = \frac{{16 - x}}{5} - 2x\)
\(\begin{array}{l}\frac{{5\left( {7x - 1} \right)}}{{5.6}} = \frac{{6\left( {16 - x} \right)}}{{6.5}} - \frac{{30.2x}}{{30}}\\5\left( {7x - 1} \right) = 6\left( {16 - x} \right) - 60x\\35x - 5 = 96 - 6x - 60x\\35x + 6x + 60x = 96 + 5\\101x = 101\\x = 1\end{array}\)
Vậy nghiệm của phương trình là \(x = 1\)
Giải bài toán bằng cách lập phương trình
Một xe tải và một xe con cùng khởi hành từ tỉnh A đến tỉnh B. Xe tải đi với vận tốc 30km/h, xe con đi với vận tốc 45km/h. Sau khi đi được \(\frac{3}{4}\) quãng đường AB, xe con tăng vận tốc 5km/h trên quãng đường còn lại thì đến B sớm hơn xe tải là 2 giờ 27 phút. Tính quãng đường AB.
Giải bài toán bằng cách lập phương trình.
Gọi quãng đường AB là x (km) (x > 0).
Biểu diễn thời gian xe tải, xe con đi theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi quãng đường AB dài x (km) (x > 0).
Thời gian xe tải đi hết quãng đường AB là \(\frac{x}{{30}}\) (giờ).
\(\frac{3}{4}\) quãng đường AB là \(\frac{3}{4}x\) (km), khi đó thời gian ô tô con đi hết \(\frac{3}{4}\) quãng đường AB là:
\(\frac{3}{4}x:45 = \frac{x}{{60}}\) (giờ)
Vận tốc xe con sau khi tăng thêm 5km/h là:
45 + 5 = 50 (km/h)
Quãng đường còn lại là: \(1 - \frac{3}{4}x = \frac{x}{4}\) (km)
Thời gian xe con đi hết \(\frac{1}{4}\) quãng đường AB là:
\(\frac{x}{4}:50 = \frac{x}{{200}}\) (h)
Vì xe con đến B sớm hơn xe tải là 2 giờ 27 phút = \(\frac{{49}}{{20}}\)h nên ta có phương trình:
\(\begin{array}{l}\frac{x}{{30}} - \left( {\frac{x}{{60}} + \frac{x}{{200}}} \right) = \frac{{49}}{{20}}\\\frac{{20x}}{{600}} - \frac{{10x}}{{600}} - \frac{{3x}}{{600}} = \frac{{1470}}{{600}}\\\frac{{7x}}{{600}} = \frac{{1470}}{{600}}\\7x = 1470\\x = 210(TM)\end{array}\)
Vậy quãng đường AB dài 210km.
Tìm m để phương trình \(2\left( {x - 1} \right) - mx = 3\):
a) Vô nghiệm
b) Có nghiệm duy nhất
Biến đổi tương đương đưa phương trình về dạng ax = b:
+ Nếu a = 0 và b ≠ 0 thì phương trình vô nghiệm.
+ Nếu a ≠ 0 thì phương trình có nghiệm duy nhất \(x = \frac{b}{a}\).
Ta có:
\(2\left( {x - 1} \right) - mx = 3\)
\(\begin{array}{l}2x - 2 - mx = 3\\2x - mx = 3 + 2\\(2 - m)x = 5\end{array}\)
a) Để phương trình \(2\left( {x - 1} \right) - mx = 3\) vô nghiệm thì:
\(2 - m = 0\) suy ra \(m = 2\).
Vậy khi m = 2 thì phương trình vô nghiệm.
b) Để phương trình \(2\left( {x - 1} \right) - mx = 3\) có nghiệm duy nhất thì:
\(2 - m \ne 0\) suy ra \(m \ne 2\).
Vậy khi \(m \ne 2\) thì phương trình có nghiệm duy nhất \(x = \frac{5}{{2 - m}}\).
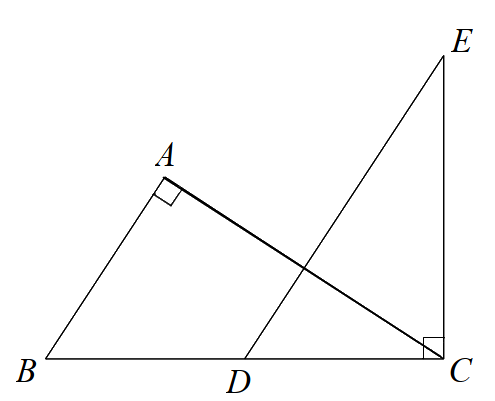
Cho \(\Delta ABC\) nhọn có AB < AC. Đường cao AH. Qua H vẽ \(HM \bot AB\) và \(HN \bot AC\).
a) Chứng minh $\Delta AMH\backsim \Delta AHB$.
b) Chứng minh \(AN.AC = A{H^2}\).
c) Vẽ đường cao BD cắt AH tại E. Qua D vẽ đường thẳng song song với MN cắt AB tại F. Chứng minh \(\widehat {AEF} = \widehat {ABC}\).
a) Chứng minh $\Delta AMH\backsim \Delta AHB\left( g.g \right)$
b) Chứng minh $\Delta ANH\backsim \Delta AHC\left( g.g \right)$ suy ra \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) suy ra \(AN.AC = A{H^2}\).
c) Áp dụng định lý Thales để chứng minh \(\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\left( { = \frac{{AD}}{{AN}}} \right)\)
Chứng minh $\Delta AFE\backsim \Delta AMH\left( c.g.c \right)$ suy ra \(\widehat {AEF} = \widehat {AHM}\) mà \(\widehat {AHM} = \widehat {ABC}\) nên \(\widehat {AEF} = \widehat {ABC}\).
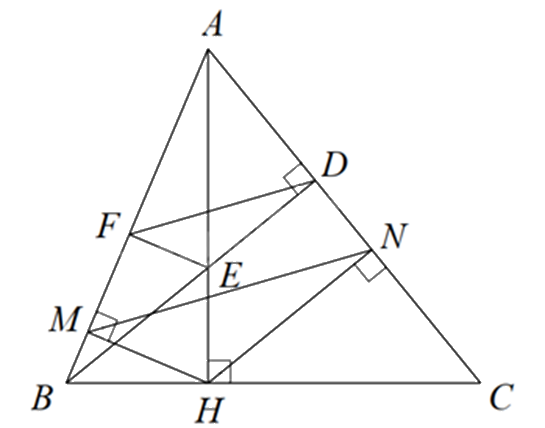
a) Xét \(\Delta AMH\) và \(\Delta AHB\) có:
\(\widehat {AMH} = \widehat {AHB}\left( { = {{90}^0}} \right)\)
\(\widehat A\) chung
suy ra $\Delta AMH\backsim \Delta AHB\left( g.g \right)$ (đpcm)
b) Xét \(\Delta ANH\) và \(\Delta AHC\) có:
\(\widehat {ANH} = \widehat {AHC}\left( { = {{90}^0}} \right)\)
\(\widehat A\) chung
suy ra $\Delta ANH\backsim \Delta AHC\left( g.g \right)$
suy ra \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) suy ra \(AN.AC = A{H^2}\) (đpcm)
c) Vì DF // NM nên \(\frac{{AF}}{{AM}} = \frac{{AD}}{{AN}}\)
Vì DE // HN nên \(\frac{{AE}}{{AH}} = \frac{{AD}}{{AN}}\)
suy ra \(\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\)
Xét \(\Delta AFE\) và \(\Delta AMH\) có:
\(\widehat A\) chung
\(\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\)
suy ra $\Delta AFE\backsim \Delta AMH\left( c.g.c \right)$ nên \(\widehat {AEF} = \widehat {AHM}\)
Mà \(\widehat {AHM} = \widehat {ABC}\)(vì $\Delta AMH\backsim \Delta AHB$)
Do đó \(\widehat {AEF} = \widehat {ABC}\) (đpcm)
Giải phương trình:
\(\left( {\frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}} \right)x = \left( {\frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}} \right)\)
Biến đổi a, b trong phương trình ax = b để tìm x.
Sử dụng kiến thức: \(\frac{1}{{a.b}} = \frac{1}{{b - a}}\left( {\frac{1}{a} - \frac{1}{b}} \right)\) với b > a
Phương trình \(\left( {\frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}} \right)x = \left( {\frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}} \right)\) có dạng ax = b với \(a = \frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}\) và \(b = \frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}\)
Ta có:
\(\begin{array}{l}a = \frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}\\ = \frac{1}{{50}}\left( {\frac{{50}}{{1.51}} + \frac{{50}}{{2.52}} + ... + \frac{{50}}{{10.60}}} \right)\\ = \frac{1}{{50}}\left[ {\left( {1 - \frac{1}{{51}}} \right) + \left( {\frac{1}{2} - \frac{1}{{52}}} \right) + ... + \left( {\frac{1}{{10}} - \frac{1}{{60}}} \right)} \right]\\ = \frac{1}{{50}}\left[ {\left( {1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{10}}} \right) - \left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}}} \right)} \right]\end{array}\)
\(\begin{array}{l}b = \frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}\\ = \frac{1}{{10}}\left( {\frac{{10}}{{1.11}} + \frac{{10}}{{2.12}} + ... + \frac{{10}}{{50.60}}} \right)\\ = \frac{1}{{10}}\left[ {\left( {1 - \frac{1}{{11}}} \right) + \left( {\frac{1}{2} - \frac{1}{{12}}} \right) + ... + \left( {\frac{1}{{50}} - \frac{1}{{60}}} \right)} \right]\\ = \frac{1}{{10}}\left[ {\left( {1 + \frac{1}{2} + ... + \frac{1}{{50}}} \right) - \left( {\frac{1}{{11}} + \frac{1}{{12}} + ... + \frac{1}{{60}}} \right)} \right]\\ = \frac{1}{{10}}\left[ {\left( {1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{10}}} \right) - \left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}}} \right)} \right]\\ = 5.\frac{1}{{50}}\left[ {\left( {1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{10}}} \right) - \left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}}} \right)} \right]\\ = 5a\end{array}\)
Phương trình trở thành: \(ax = 5a\) suy ra \(x = 5\).
Vậy nghiệm của phương trình \(\left( {\frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}} \right)x = \left( {\frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}} \right)\) là \(x = 5\).
Đề thi học kì 2 Toán 8 - Đề số 1 - Cánh diều là một bài kiểm tra quan trọng đánh giá kiến thức và kỹ năng giải toán của học sinh sau một học kỳ học tập. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính như đa thức, phân thức đại số, phương trình bậc nhất một ẩn, bất phương trình bậc nhất một ẩn, hệ phương trình bậc nhất hai ẩn, hàm số bậc nhất, và ứng dụng thực tế của đại số.
Cấu trúc đề thi thường bao gồm:
Trọng tâm kiến thức cần nắm vững để làm tốt đề thi này bao gồm:
Để giải các bài tập về đa thức và phân thức đại số, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia đa thức và phân thức. Ví dụ:
Bài tập: Rút gọn biểu thức: (x + 2)(x - 2) + x2
Giải: (x + 2)(x - 2) + x2 = x2 - 4 + x2 = 2x2 - 4
Để giải phương trình bậc nhất một ẩn, học sinh cần thực hiện các phép biến đổi tương đương để đưa phương trình về dạng x = a. Ví dụ:
Bài tập: Giải phương trình: 2x + 3 = 7
Giải: 2x + 3 = 7 => 2x = 4 => x = 2
Để giải hệ phương trình bậc nhất hai ẩn, học sinh có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số. Ví dụ:
Bài tập: Giải hệ phương trình: x + y = 5 x - y = 1
Giải: Cộng hai phương trình, ta được: 2x = 6 => x = 3. Thay x = 3 vào phương trình x + y = 5, ta được: 3 + y = 5 => y = 2. Vậy nghiệm của hệ phương trình là (x, y) = (3, 2).
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Chúc các em học sinh ôn thi tốt và đạt kết quả cao trong kỳ thi học kì 2 Toán 8!