Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 8 Cánh diều - Đề số 7, một công cụ ôn luyện tuyệt vời giúp học sinh nắm vững kiến thức và tự tin bước vào kỳ thi. Đề thi được biên soạn theo chương trình học mới, bám sát nội dung sách giáo khoa và có đáp án chi tiết đi kèm.
Với đề thi này, các em học sinh có thể tự đánh giá năng lực, rèn luyện kỹ năng giải đề và làm quen với cấu trúc đề thi thực tế.
Bậc của đơn thức \(2023x{y^3}{z^4}\) là:
7.
12.
8.
9.
Đồ thị hàm số \(y = - 2x + 3\) song song với đồ thị hàm số:
\(y = - 2x + 1\).
\(y = 2x + 3\).
\(y = - 2x + 3\).
\(y = 4x + 3\).
Điều kiện xác định của biểu thức \(Q = \frac{{2024}}{{x - 2}}\) là:
\(x \ne 0\).
\(x \ne 0;x \ne 2\).
\(x \ne - 2\).
\(x \ne 2\).
Kết quả của phép nhân \(\left( {x - 2y} \right)\left( {2x + y} \right)\) là:
\(2{x^2} - 2{y^2}\).
\(2{x^2} - 3xy - 2{y^2}\).
\(2{x^2} - 3xy + 2{y^2}\).
\(2{x^2} - 5xy - 2{y^2}\).
Trong các hàm số sau, hàm số bậc nhất là:
\(y = - 4x + 3\).
\(y = \frac{2}{x} + 3\).
\(y = 2{x^2} + 1\).
\(y = \left| x \right| - 2\).
Cho đa thức P thỏa mãn \(\left( {x - 1} \right).P = {x^3} - 1\). Khi đó đa thức P là:
\({x^2} - x + 1\).
\({x^2} + 2x + 1\).
\({x^2} + x + 1\).
\({x^2} - 2x + 1\).
Hình nào sau đây là hình vuông?
Tứ giác có ba góc vuông.
Hình bình hành có một góc vuông.
Hình thang cân có một góc vuông.
Hình chữ nhật có hai cạnh kề bằng nhau.
Cho một hình chóp tam giác đều có diện tích đáy là \(15c{m^2}\) và chiều cao là 8cm. Khi đó thể tích của hình chóp tam giác đều đó là:
\(48c{m^3}\).
\(30c{m^3}\).
\(60c{m^3}\).
\(40c{m^3}\).
Cho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây?
MN.
NQ.
MQ.
NP.
Tứ giác ABCD có \(\widehat A = 60^\circ ;\widehat B = 70^\circ ;\widehat C = 80^\circ \). Khi đó \(\widehat D\) bằng
\(130^\circ \).
\(160^\circ \).
\(150^\circ \).
\(140^\circ \).
Cho hình thoi ABCD có \(AC = 6cm;BD = 8cm\). Khi đó cạnh của hình thoi bằng:
5cm.
6cm.
8cm.
10cm.
Rút gọn phân thức \(\frac{{3{{\left( {b - a} \right)}^2}}}{{9\left( {a - b} \right)}}\), ta được kết quả là:
\(\frac{{b - a}}{3}\).
\(\frac{{a - b}}{6}\).
\(3\left( {a - b} \right)\).
\(\frac{{a - b}}{3}\).
Cho biểu thức \(P = \frac{x}{{x - 1}} + \frac{3}{{x + 1}} - \frac{{6x - 4}}{{{x^2} - 1}}\) với \(x \ne \pm 1\).
a) Rút gọn P.
b) Tính giá trị của P khi \(x = 2\).
Phân tích mỗi đa thức sau thành nhân tử:
a) \(3{x^2}y - 9x{y^2}\)
b) \({x^2} - 2x - {y^2} + 2y\)
Biết rằng đồ thị hàm số \(y = ax - 2\) đi qua điểm \(K\left( {\frac{1}{2}; - 1} \right)\). Tìm a và vẽ đồ thị của hàm số với giá trị a vừa tìm được.
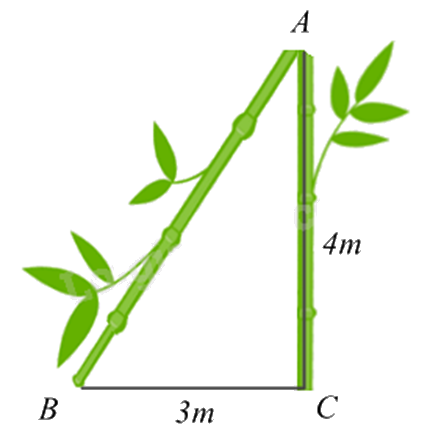
1. Sau trận bão lớn, một cái cây bị gãy ngang (như hình vẽ). Ngọn cây chạm mặt đất cách gốc 3m. Đoạn thân cây còn lại (vuông góc với mặt đất) người ta đo được là 4m. Hỏi lúc đầu cây cao bao nhiêu mét?
2. Cho \(\Delta ABC\) vuông tại A có AB < AC, đường cao AH \(\left( {H \in BC} \right)\). Kẻ \(HM \bot AB\left( {M \in AB} \right)\), \(HN \bot AC\left( {N \in AC} \right)\).
a) Chứng minh AMHN là hình chữ nhật.
b) Gọi I là trung điểm của HC, trên tia đối của tia IA lấy điểm K sao cho I là trung điểm của AK. Chứng minh KH // AC và MN = CK.
c) Gọi O là giao điểm của AH và MN, gọi D là giao điểm của CO và AK. Chứng minh AK = 3AD.
Tính giá trị lớn nhất của biểu thức \(B = 2014 - 2{x^2} - {y^2} + 2xy - 8x + 2y\).
Bậc của đơn thức \(2023x{y^3}{z^4}\) là:
7.
12.
8.
9.
Đáp án : C
Bậc của đơn thức là tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0.
Đơn thức \(2023x{y^3}{z^4}\) có phần biến là \(x{y^3}{z^4}\) nên bậc là: \(1 + 3 + 4 = 8\).
Đáp án C
Đồ thị hàm số \(y = - 2x + 3\) song song với đồ thị hàm số:
\(y = - 2x + 1\).
\(y = 2x + 3\).
\(y = - 2x + 3\).
\(y = 4x + 3\).
Đáp án : A
Đồ thị hàm số \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song nếu \(a = a',b \ne b'\).
Đồ thị hàm số \(y = - 2x + 3\) song song với đồ thị hàm số \(y = - 2x + 1\) vì hệ số của x bằng nhau (\( = - 2\)) và hệ số tự do khác nhau (\(3 \ne 1\)).
Đáp án A
Điều kiện xác định của biểu thức \(Q = \frac{{2024}}{{x - 2}}\) là:
\(x \ne 0\).
\(x \ne 0;x \ne 2\).
\(x \ne - 2\).
\(x \ne 2\).
Đáp án : D
Phân thức xác định khi mẫu thức khác 0.
Phân thức \(Q = \frac{{2024}}{{x - 2}}\) xác định khi \(x - 2 \ne 0\), suy ra \(x \ne 2\).
Đáp án D
Kết quả của phép nhân \(\left( {x - 2y} \right)\left( {2x + y} \right)\) là:
\(2{x^2} - 2{y^2}\).
\(2{x^2} - 3xy - 2{y^2}\).
\(2{x^2} - 3xy + 2{y^2}\).
\(2{x^2} - 5xy - 2{y^2}\).
Đáp án : B
Để nhân hai đa thức với nhau, ta nhân lần lượt các hạng tử của đa thức này với các hạng tử của đa thức kia.
Ta có:
\(\left( {x - 2y} \right)\left( {2x + y} \right) = 2{x^2} - 4xy + xy - 2{y^2} = 2{x^2} - 3xy - 2{y^2}\)
Đáp án B
Trong các hàm số sau, hàm số bậc nhất là:
\(y = - 4x + 3\).
\(y = \frac{2}{x} + 3\).
\(y = 2{x^2} + 1\).
\(y = \left| x \right| - 2\).
Đáp án : A
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\).
Trong các hàm số trên, chỉ có hàm số \(y = - 4x + 3\) là hàm số bậc nhất.
Đáp án A
Cho đa thức P thỏa mãn \(\left( {x - 1} \right).P = {x^3} - 1\). Khi đó đa thức P là:
\({x^2} - x + 1\).
\({x^2} + 2x + 1\).
\({x^2} + x + 1\).
\({x^2} - 2x + 1\).
Đáp án : C
Thực hiện phân tích \({x^3} - 1\) theo hằng đẳng thức hiệu hai lập phương, sau đó chia cho \(x - 1\).
Ta có:
\(\begin{array}{l}\left( {x - 1} \right).P = {x^3} - 1\\\left( {x - 1} \right).P = \left( {x - 1} \right)\left( {{x^2} + x + 1} \right)\\P = \frac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)\,}}{{x - 1}}\\P = {x^2} + x + 1\end{array}\)
Đáp án C
Hình nào sau đây là hình vuông?
Tứ giác có ba góc vuông.
Hình bình hành có một góc vuông.
Hình thang cân có một góc vuông.
Hình chữ nhật có hai cạnh kề bằng nhau.
Đáp án : D
Dựa vào dấu hiệu nhận biết hình vuông.
Tứ giác có ba góc vuông là hình chữ nhật nên A sai.
Hình bình hành có một góc vuông là hình chữ nhật nên B sai.
Hình thang cân có một góc vuông là hình chữ nhật nên C sai.
Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông nên D đúng.
Đáp án D
Cho một hình chóp tam giác đều có diện tích đáy là \(15c{m^2}\) và chiều cao là 8cm. Khi đó thể tích của hình chóp tam giác đều đó là:
\(48c{m^3}\).
\(30c{m^3}\).
\(60c{m^3}\).
\(40c{m^3}\).
Đáp án : D
Thể tích hình chóp tam giác đều bằng \(\frac{1}{3}\).Sđáy. chiều cao.
Thể tích hình chóp tam giác đều là:
\(\frac{1}{3}.15.8 = 40\left( {c{m^3}} \right)\)
Đáp án D
Cho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây?
MN.
NQ.
MQ.
NP.
Đáp án : B
Dựa vào đặc điểm hình chữ nhật: hai đường chéo bằng nhau.
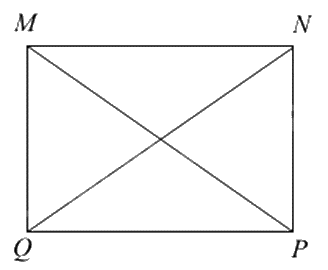
Vì MNPQ là hình chữ nhật nên hai đường chéo bằng nhau, do đó MP = NQ.
Đáp án B
Tứ giác ABCD có \(\widehat A = 60^\circ ;\widehat B = 70^\circ ;\widehat C = 80^\circ \). Khi đó \(\widehat D\) bằng
\(130^\circ \).
\(160^\circ \).
\(150^\circ \).
\(140^\circ \).
Đáp án : C
Sử dụng định lí Tổng bốn góc trong một tứ giác bằng \(360^\circ \).
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Suy ra
\(\begin{array}{c}\widehat D = 360^\circ - \widehat A - \widehat B - \widehat C\\ = 360^\circ - 60^\circ - 70^\circ - 80^\circ \\ = 150^\circ \end{array}\)
Đáp án C
Cho hình thoi ABCD có \(AC = 6cm;BD = 8cm\). Khi đó cạnh của hình thoi bằng:
5cm.
6cm.
8cm.
10cm.
Đáp án : A
Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Gọi O là giao điểm của hai đường chéo, khi đó ta tính được độ dài hai cạnh góc vuông OA, OB.
Áp dụng định lí Pythagore vào tam giác AOB, ta tính được AB là cạnh của hình thoi.
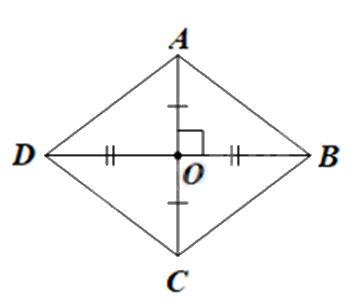
Gọi O là giao điểm của hai đường chéo, khi đó \(AO = \frac{1}{2}AC = \frac{1}{2}.6 = 3\left( {cm} \right)\); \(BO = \frac{1}{2}BD = \frac{1}{2}.8 = 4\left( {cm} \right)\).
Áp dụng định lí Pythagore vào tam giác AOB vuông tại O, ta có:
\(A{B^2} = A{O^2} + B{O^2} = {3^2} + {4^2} = 25\)
Suy ra \(AB = 5\left( {cm} \right)\)
Đáp án A
Rút gọn phân thức \(\frac{{3{{\left( {b - a} \right)}^2}}}{{9\left( {a - b} \right)}}\), ta được kết quả là:
\(\frac{{b - a}}{3}\).
\(\frac{{a - b}}{6}\).
\(3\left( {a - b} \right)\).
\(\frac{{a - b}}{3}\).
Đáp án : D
Sử dụng đẳng thức \({\left( {a - b} \right)^2} = {\left( {b - a} \right)^2}\) và tính chất \(\frac{{A.M}}{{B.M}} = \frac{A}{B}\) để rút gọn phân thức.
Ta có: \(\frac{{3{{\left( {b - a} \right)}^2}}}{{9\left( {a - b} \right)}} = \frac{{3{{\left( {a - b} \right)}^2}}}{{9\left( {a - b} \right)}} = \frac{{a - b}}{3}\).
Đáp án D
Cho biểu thức \(P = \frac{x}{{x - 1}} + \frac{3}{{x + 1}} - \frac{{6x - 4}}{{{x^2} - 1}}\) với \(x \ne \pm 1\).
a) Rút gọn P.
b) Tính giá trị của P khi \(x = 2\).
a) Thực hiện quy đồng mẫu để rút gọn P.
b) Kiểm tra xem \(x = 2\) có thỏa mãn điều kiện hay không.
Thay \(x = 2\) vào P để tính giá trị.
a) Ta có:
\(\begin{array}{l}P = \frac{x}{{x - 1}} + \frac{3}{{x + 1}} - \frac{{6x - 4}}{{{x^2} - 1}}\\ = \frac{{x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \frac{{3\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \frac{{6x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} + x + 3x - 3 - 6x + 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} + \left( {x + 3x - 6x} \right) + \left( { - 3 + 4} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} - 2x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{x - 1}}{{x + 1}}\end{array}\)
b) Ta thấy \(x = 2\) thỏa mãn điều kiện \(x \ne \pm 1\) của P.
Thay \(x = 2\) vào biểu thức P, ta được:
\(P = \frac{{2 - 1}}{{2 + 1}} = \frac{1}{3}\)
Vậy với \(x = 2\) thì \(P = \frac{1}{3}\).
Phân tích mỗi đa thức sau thành nhân tử:
a) \(3{x^2}y - 9x{y^2}\)
b) \({x^2} - 2x - {y^2} + 2y\)
a) Sử dụng phương pháp đặt nhân tử chung để phân tích.
b) Sử dụng kết hợp phương pháp nhóm hạng tử và sử dụng hằng đẳng thức để phân tích đa thức thành nhân tử.
a) \(3{x^2}y - 9x{y^2}\)\( = 3xy\left( {x - 3y} \right)\)
b) \({x^2} - 2x - {y^2} + 2y\)
\(\begin{array}{l}{x^2} - 2x - {y^2} + 2y\\ = \left( {{x^2} - {y^2}} \right) - \left( {2x - 2y} \right)\\ = \left( {x - y} \right)\left( {x + y} \right) - 2\left( {x - y} \right)\\ = \left( {x - y} \right)\left( {x + y - 2} \right)\end{array}\)
Biết rằng đồ thị hàm số \(y = ax - 2\) đi qua điểm \(K\left( {\frac{1}{2}; - 1} \right)\). Tìm a và vẽ đồ thị của hàm số với giá trị a vừa tìm được.
- Thay tọa độ của K vào hàm số để tìm a.
- Vẽ đồ thị hàm số:
+ Xác định tọa độ hai điểm thuộc đồ thị hàm số.
+ Vẽ trục tọa độ, xác định hai điểm trên trục tọa độ, vẽ đường thẳng đi qua hai điểm đó, ta được đồ thị hàm số.
Do đồ thị hàm số \(y = ax - 2\) đi qua điểm \(K\left( {\frac{1}{2}; - 1} \right)\) nên thay \(x = \frac{1}{2};y = - 1\) vào \(y = ax - 2\) ta được:
\(\begin{array}{l} - 1 = a.\frac{1}{2} - 2\\\frac{1}{2}a = - 1 + 2\\\frac{1}{2}a = 1\\a = 2\end{array}\)
Vậy a = 2 là giá trị cần tìm.
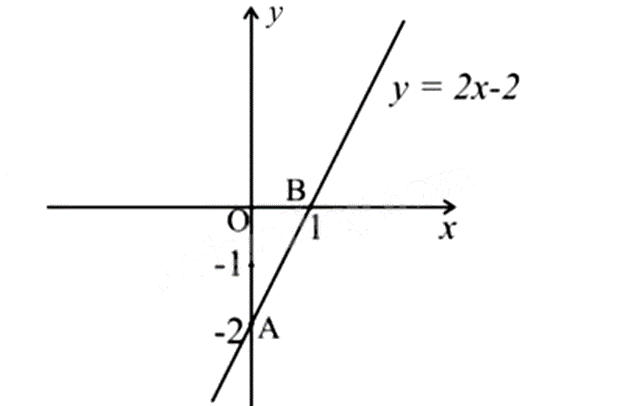
Với a = 2, ta có: \(y = 2x - 2\).
+ Cho \(x = 0\) suy ra \(y = 2.0 - 2 = - 2\). Đồ thị hàm số đi qua điểm \(A\left( {0; - 2} \right)\)
+ Cho \(y = 0\) suy ra \(2x - 2 = 0\), khi đó \(x = 1\). Đồ thị hàm số đi qua điểm \(B\left( {1;0} \right)\)
Vẽ đồ thị hàm số.
Đồ thị hàm số là đường thẳng đi qua hai điểm A và B.
1. Sau trận bão lớn, một cái cây bị gãy ngang (như hình vẽ). Ngọn cây chạm mặt đất cách gốc 3m. Đoạn thân cây còn lại (vuông góc với mặt đất) người ta đo được là 4m. Hỏi lúc đầu cây cao bao nhiêu mét?
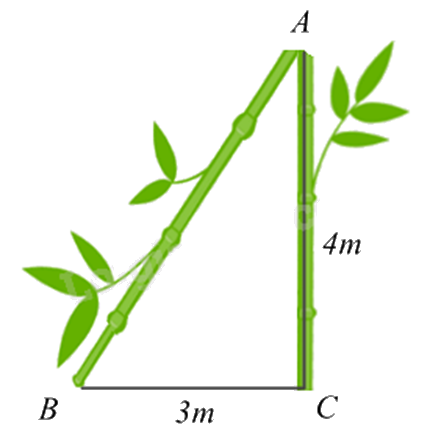
2. Cho \(\Delta ABC\) vuông tại A có AB < AC, đường cao AH \(\left( {H \in BC} \right)\). Kẻ \(HM \bot AB\left( {M \in AB} \right)\), \(HN \bot AC\left( {N \in AC} \right)\).
a) Chứng minh AMHN là hình chữ nhật.
b) Gọi I là trung điểm của HC, trên tia đối của tia IA lấy điểm K sao cho I là trung điểm của AK. Chứng minh KH // AC và MN = CK.
c) Gọi O là giao điểm của AH và MN, gọi D là giao điểm của CO và AK. Chứng minh AK = 3AD.
1. Áp dụng định lí Pythagore trong tam giác vuông để tính AB. Chiều cao của cây lúc đầu bằng tổng đoạn AB và AC.
2.
a) Chứng minh AMHN có 3 góc vuông nên là hình chữ nhật.
b) - Chứng minh tứ giác AHKC là hình bình hành suy ra AC // HK và AH = CK.
- Chỉ ra AH = MN (do AMHN là hình chữ nhật) suy ra CK = MN.
c) Chỉ ra D là trọng tâm của tam giác AHC, suy ra AD = \(\frac{2}{3}\) AI.
Chỉ ra \(AI = \frac{1}{2}AK\) nên AK = 3AD.
1.
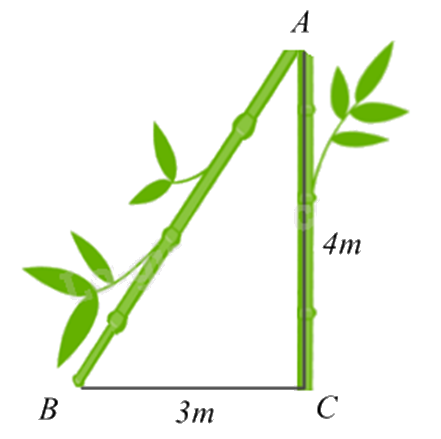
Xét tam giác ABC vuông tại C. Áp dụng định lí Pythagore, ta có:
\(A{B^2} = A{C^2} + B{C^2} = {4^2} + {3^2} = 25\)
suy ra \(AB = 5\left( m \right)\) (vì \(AB > 0\))
Chiều cao của cây lúc đầu là: AC + AB = 4 + 5 = 9 (m).
2.
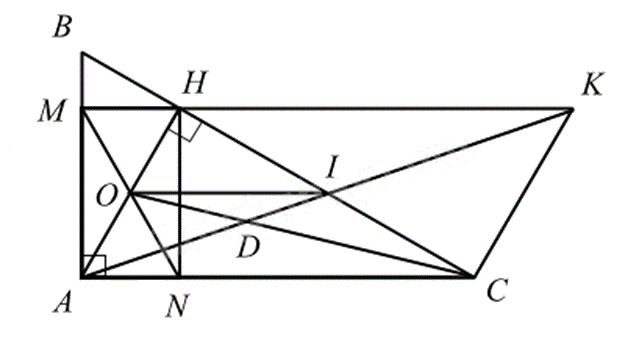
a) Vì tam giác ABC vuông tại A nên \(\widehat A = 90^\circ \).
Vì \(HM \bot AB\left( {M \in AB} \right)\) \(HN \bot AC\left( {N \in AC} \right)\) nên \(\widehat {HMA} = \widehat {HNA} = 90^\circ \).
Tứ giác AMHN có: \(\widehat A = \widehat {HMA} = \widehat {HNA} = 90^\circ \) nên là hình chữ nhật.
b) Xét tứ giác AHKC có: HC cắt AK tại I và AI = IK (gt), HI = IC (gt) suy ra tứ giác AHKC là hình bình hành, do đó \(AC//HK\) và AH = CK.
Mà AH = MN (hai đường chéo của hình chữ nhật AMHN bằng nhau) nên MN = CK.
c) Xét tam giác AHC có CO và AI là hai đường trung tuyến và CO cắt AI tại D nên D là trọng tâm của tam giác AHC. Do đó \(AD = \frac{2}{3}AI\) (tính chất của trọng tâm)
Mà \(AI = \frac{1}{2}AK\) (do I là trung điểm của AK)
Do đó \(AD = \frac{2}{3}.\frac{1}{2}AK = \frac{1}{3}AK\) hay \(AK = 3AD\).
Tính giá trị lớn nhất của biểu thức \(B = 2014 - 2{x^2} - {y^2} + 2xy - 8x + 2y\).
Sử dụng các hằng đẳng thức đáng nhớ để biến đổi đưa biểu thức về dạng \(A - B\left( x \right) - C\left( x \right)\) với \(B\left( x \right),C\left( x \right)\) là hai biểu thức bậc hai.
Khi đó \(A - B\left( x \right) - C\left( x \right) \le A\), khi đó giá trị giá trị lớn nhất của biểu thức là A khi \(B\left( x \right) = 0\) và \(C\left( x \right) = 0\).
Ta có:
\(\begin{array}{c}B = 2014 - 2{x^2} - {y^2} + 2xy - 8x + 2y\\ = 2024 - 1 - 9 - {x^2} - {x^2} - {y^2} + 2xy - 8x + 2y\\ = 2024 - \left( {{x^2} - 2xy + {y^2}} \right) - 1 - {x^2} - 8x + 2y - 9\\ = 2024 - \left[ {{{\left( {x - y} \right)}^2} - 2x + 2y - 1} \right] - {x^2} - 6x - 9\\ = 2024 - \left[ {{{\left( {x - y} \right)}^2} + 2\left( {x - y} \right) + 1} \right] - \left( {{x^2} + 6x + 9} \right)\\ = 2024 - {\left( {x - y + 1} \right)^2} - {\left( {x + 3} \right)^2}\end{array}\)
Vì \({\left( {x - y + 1} \right)^2} \ge 0\) với mọi x, y và \({\left( {x + 3} \right)^2} \ge 0\) với mọi x nên \(B = 2024 - {\left( {x - y + 1} \right)^2} - {\left( {x + 3} \right)^2} \le 0\) với mọi x, y.
Dấu “=” xảy ra khi \(x + 3 = 0\) và \(x - y + 1 = 0\), suy ra \(x = - 3\) và \(y = - 2\).
Vậy giá trị lớn nhất của B = 2024 khi \(x = - 3\) và \(y = - 2\).
Kỳ thi học kì 1 Toán 8 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh trong nửa học kỳ đầu tiên. Việc làm quen với các dạng đề thi khác nhau, đặc biệt là các đề thi được biên soạn theo sách Cánh diều, là vô cùng cần thiết để đạt kết quả tốt nhất.
Đề thi học kì 1 Toán 8 Cánh diều - Đề số 7 bao gồm các dạng bài tập thuộc các chủ đề chính đã được học trong chương trình Toán 8 học kì 1, như:
Dưới đây là một số câu hỏi tiêu biểu trong đề thi và hướng dẫn giải chi tiết:
Phân tích đa thức sau thành nhân tử: x2 - 4x + 4
Hướng dẫn giải:
Ta có: x2 - 4x + 4 = (x - 2)2
Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Đường thẳng DE cắt AC tại I. Chứng minh rằng AI = IC.
Hướng dẫn giải:
Xét tam giác ABE, ta có E là trung điểm của AB. Do đó, AE = EB.
Xét tam giác ABI và tam giác CEI, ta có:
Vậy, tam giác ABI đồng dạng với tam giác CEI (g-c-g). Suy ra AI = IC.
Giải phương trình: 2x + 5 = 11
Hướng dẫn giải:
2x + 5 = 11
2x = 11 - 5
2x = 6
x = 3
... (Tiếp tục phân tích và giải các câu hỏi khác trong đề thi)
Lợi ích khi luyện tập với đề thi này:
Lời khuyên khi làm bài thi:
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục kiến thức. Chúc các em học sinh ôn thi tốt và đạt kết quả cao trong kỳ thi học kì 1 Toán 8!
Ngoài ra, các em có thể tham khảo thêm các đề thi khác và tài liệu học tập hữu ích tại website của chúng tôi. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều điều thú vị và bổ ích.
| Chủ đề | Số câu hỏi |
|---|---|
| Đại số | 5 |
| Hình học | 5 |