Bài trắc nghiệm này được thiết kế để giúp học sinh lớp 8 ôn tập và củng cố kiến thức về tứ giác trong chương trình Toán 8 Chân trời sáng tạo. Với các câu hỏi đa dạng, từ dễ đến khó, bạn sẽ được kiểm tra khả năng hiểu và vận dụng các định nghĩa, tính chất của tứ giác.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm chất lượng cao, kèm đáp án chi tiết, giúp bạn tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Hãy chọn câu sai trong các câu sau
Các góc của tứ giác có thể là
4 góc nhọn.
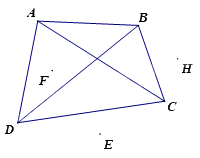
Cho hình vẽ dưới đây. Chọn khẳng định sai trong các câu sau
Chọn câu đúng trong các câu sau khi nói về định nghĩa tứ giác ABCD:
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA và 4 góc tại đỉnh bằng nhau.
Cho hình vẽ sau, chọn câu đúng:
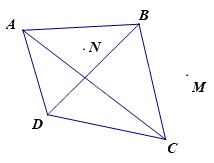
Hai cạnh đối nhau: AB, BC.
Hai cạnh kề nhau: BC, DA.
Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
Điểm M nằm trong tứ giác ABCD và điểm N nằm ngoài tứ giác ABCD
Cho tứ giác ABCD trong đó: \(\widehat A + \widehat B = {140^o}\). Tổng \(\widehat C + \widehat D\) bằng:
Cho tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {117^o};\widehat C = {71^o}\). Số đo góc ngoài tại đỉnh D bằng:
Tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {123^o};\widehat D = {20^o}\). Số đo của góc C là:
Tứ giác ABCD có \(\widehat A = {100^o};\widehat B = {120^o};\widehat C - \widehat D = {20^o}\). Số đo các góc C, D là:
Tứ giác ABCD có các cạnh tỉ lệ với 3, 5, 7, 9 và chu vi là 240 m. Cạnh ngắn nhất là:
Cho tứ giác ABCD có góc ngoài tại đỉnh D bằng \({50^o}\) ; góc ngoài tại đỉnh A bằng \({100^o}\) . Tỉnh tổng \(\widehat A + \widehat D\) trong tứ giác ABCD là:
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng:
Cho tứ giác ABCD biết số đo của các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) tỉ lệ thuận với 4, 3, 5, 6. Khi đó số đo các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) lần lượt là:
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là:
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là \({200^o}\) . Tính số đo các góc ngoài tại hai đỉnh A, C là:
Tứ giác ABCD có AB = BC; CD = DA , \(\widehat B = {100^o};\widehat D = {70^o}\) . Tính \(\widehat A{,^{}}\widehat C\) ?
Tam giác ABC có Â = 600, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc \(\widehat {BIC}{;^{}}\widehat {BKC}\)
Tứ giác ABCD có: \(\widehat A + \widehat C = {60^o}\) Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.
Lời giải và đáp án
Hãy chọn câu sai trong các câu sau
Đáp án : B
Các góc của tứ giác có thể là
4 góc nhọn.
Đáp án : C
Các góc của tứ giác có thể là 4 góc vuông vì khi đó tổng các góc của tứ giác này bằng 360o.
Các trường hợp còn lại không thỏa mãn định lí tổng các góc trong tam giác.
Cho hình vẽ dưới đây. Chọn khẳng định sai trong các câu sau
Đáp án : D
Chọn câu đúng trong các câu sau khi nói về định nghĩa tứ giác ABCD:
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA và 4 góc tại đỉnh bằng nhau.
Đáp án : B
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Cho hình vẽ sau, chọn câu đúng:
Hai cạnh đối nhau: AB, BC.
Hai cạnh kề nhau: BC, DA.
Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
Điểm M nằm trong tứ giác ABCD và điểm N nằm ngoài tứ giác ABCD
Đáp án : C
Từ hình vẽ ta thấy: Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
Cho tứ giác ABCD trong đó: \(\widehat A + \widehat B = {140^o}\). Tổng \(\widehat C + \widehat D\) bằng:
Đáp án : A
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\ \Rightarrow \widehat C + \widehat D = {360^o} - \left( {\widehat A + \widehat B} \right) = {360^o} - {140^o} = {220^o}\end{array}\)
Tổng các góc trong một tứ giác bằng \({360^o}\)
Cho tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {117^o};\widehat C = {71^o}\). Số đo góc ngoài tại đỉnh D bằng:
Đáp án : C
Tính góc D trong tứ giác ABCD. Từ đó góc ngoài tại đỉnh D bằng \({180^o}\) trừ đi góc D trong tứ giác ABCD.
Góc ngoài và góc trong tứ giác tại một đỉnh là hai góc kề bù.
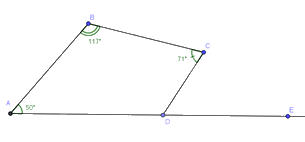
\(\widehat {C{{D}}E}\) là góc ngoài đỉnh D. Tứ giác ABCD có:
\(\begin{array}{l}\widehat D = {360^o} - \left( {\widehat A + \widehat B + \widehat C} \right)\\\widehat D = {360^o} - \left( {{{50}^o} + {{117}^o} + {{71}^o}} \right)\\\widehat D = {122^o}\end{array}\)
Vì \(\widehat {A{{D}}C}\) và \(\widehat {C{{D}}E}\) là hai góc kề bù nên:
\(\widehat {C{{D}}E} = {180^o} - \widehat D = {180^o} - {122^o} = {58^o}\)
Tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {123^o};\widehat D = {20^o}\). Số đo của góc C là:
Đáp án : B
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\ \Rightarrow \widehat C = {360^o} - \widehat A - \widehat B - \widehat D = {360^o} - {50^o} - {123^o} - {20^o} = {167^o}\end{array}\)
Tứ giác ABCD có \(\widehat A = {100^o};\widehat B = {120^o};\widehat C - \widehat D = {20^o}\). Số đo các góc C, D là:
Đáp án : C
Trong tứ giác ABCD ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Suy ra \(\widehat C + \widehat D = {360^o} - \widehat A - \widehat B = {360^o} - {100^o} - {120^o} = {140^o}(1)\)
Mà \(\widehat C - \widehat D = {20^o}\)(2)
Từ (1), (2) suy ra: \(\widehat C = \frac{140^o + 20^o}{2} = {80^o};\widehat D = \frac{140^o - 20^o}{2} = {60^o}\).
Tứ giác ABCD có các cạnh tỉ lệ với 3, 5, 7, 9 và chu vi là 240 m. Cạnh ngắn nhất là:
Đáp án : D
Gọi các cạnh AB, BC, CD, DA theo tỉ lệ 3, 5, 7, 9 nên ta có:
\(\frac{{AB}}{3} = \frac{{BC}}{5} = \frac{{C{{D}}}}{7} = \frac{{DA}}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{AB}}{3} = \frac{{BC}}{5} = \frac{{C{{D}}}}{7} = \frac{{DA}}{9} = \frac{{AB + BC + C{{D}} + DA}}{{3 + 5 + 7 + 9}} = \frac{{240}}{{24}} = 10\)
Suy ra: AB = 3. 10 = 30 cm
BC = 5 .10 = 50 cm
CD = 7. 10 = 70 cm
DA = 9 .10 = 90 cm
Vậy cạnh ngắn nhất là canh AB có độ dài 30 cm
Cho tứ giác ABCD có góc ngoài tại đỉnh D bằng \({50^o}\) ; góc ngoài tại đỉnh A bằng \({100^o}\) . Tỉnh tổng \(\widehat A + \widehat D\) trong tứ giác ABCD là:
Đáp án : D
Tổng hai góc trong và góc ngoài tại một đỉnh của tứ giác bằng \({180^o}\)
Vì góc ngoài đỉnh D bằng \({50^o}\) nên góc trong tại đỉnh D là: \(\widehat D = {180^o} - {50^o} = {130^o}\)
Vì góc ngoài tại đỉnh A bằng \({100^o}\) nên góc trong tại đỉnh A là: \(\widehat A = {180^o} - {100^o} = {80^o}\)
Suy ra: \(\widehat A + \widehat D = {80^o} + {130^o} = {210^o}\)
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng:
Đáp án : A
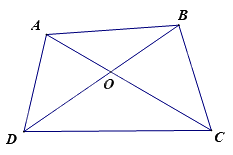
Xét tam giác ABC:
\(AB + BC > AC\) (bất đẳng thức tam giác)
Tương tự, lần lượt các tam giác BCD, CDA, DAB ta có:
\(\begin{array}{l}BC + C{{D}} > B{{D}}\\C{{D}} + DA > CA\\DA + AB > DB\end{array}\)
Cộng vế với vế ta được các bất đẳng thức trên ta được:
\(\begin{array}{l}AB + BC + C{{D}} + C{{D}} + DA + DA + AB > AC + B{{D}} + CA + DB\\ \Leftrightarrow 2\left( {AB + BC + C{{D}} + DA} \right) > 2\left( {AC + B{{D}}} \right)\\ \Leftrightarrow AB + BC + C{{D}} + DA > AC + B{{D}}\end{array}\)
Mà: \(AC + B{{D}} = OA + OC + OB + O{{D}}\) (hệ thức cộng đoạn thẳng)
\( \Leftrightarrow OA + OB + OC + O{{D}} < AB + BC + C{{D}} + DA\)
Vậy ta có: \(OA + OB + OC + O{{D}} < AB + BC + C{{D}} + DA\)
Cho tứ giác ABCD biết số đo của các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) tỉ lệ thuận với 4, 3, 5, 6. Khi đó số đo các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) lần lượt là:
Đáp án : A
\(\frac{{\widehat A}}{4} = \frac{{\widehat B}}{3} = \frac{{\widehat C}}{5} = \frac{{\widehat D}}{6} = \frac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{18}} = \frac{{{{360}^o}}}{{18}} = {20^o}\)
Do đó:
\(\begin{array}{l}\widehat A = {20^o}.4 = {80^o}\\\widehat B = {20^o}.3 = {60^o}\\\widehat C = {20^o}.5 = {100^o}\\\widehat D = {20^o}.6 = {120^o}\end{array}\)
Nên số đo các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) lần lượt là \({80^o}{;^{}}{60^o}{;^{}}{100^o}{;^{}}{120^o}\)
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
Đáp án : B
Sử dụng định lí Pytago trong tam giác vuông.
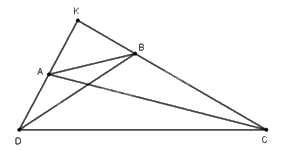
Gọi K là giao điểm AD, BC.
Vì \(\widehat C + \widehat D = {90^o}\) nên \(\widehat K = {90^o}\)
Áp dụng định lí Pytago trong tam giác vuông vào các tam giác:
+ ΔKAC vuông tại K ta có: AC2 = KC2 + KA2.
+ ΔKBD vuông tại K ta có: BD2 = KB2 + KD2.
+ ΔKBA vuông tại K ta có: BA2 = KA2 + KB2.
+ ΔKBD vuông tại K ta có: CD2 = KC2 + KD2.
Từ đó AC2+ BD2 = KC2 + KA2 + KB2 + KD2
= (KB2 +KA2) + (KD2 + KC2) = AB2 + DC2.
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là:
Đáp án : D
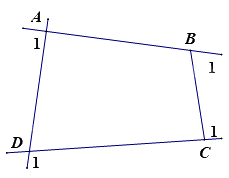
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là: \(\widehat {{A_1}};\widehat {{B_1}};\widehat {{C_1}};\widehat {{D_1}}\) .
Khi đó ta có:
\(\begin{array}{l}\widehat A + \widehat {{A_1}} = {180^o} \Rightarrow \widehat {{A_1}} = {180^o} - \widehat A\\\widehat B + \widehat {{B_1}} = {180^o} \Rightarrow \widehat {{B_1}} = {180^o} - \widehat B\\\widehat C + \widehat {{C_1}} = {180^o} \Rightarrow \widehat {{C_1}} = {180^o} - \widehat C\\\widehat D + \widehat {{D_1}} = {180^o} \Rightarrow \widehat {{D_1}} = {180^o} - \widehat D\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = \left( {{{180}^o} - \widehat A} \right) + \left( {{{180}^o} - \widehat B} \right) + \left( {{{180}^o} - \widehat C} \right) + \left( {{{180}^o} - \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - {360^o} = {360^o}\end{array}\)
Vậy số đo 4 góc ngoài tứ giác tại 4 đỉnh A, B, C, D bằng \({360^o}\)
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là \({200^o}\) . Tính số đo các góc ngoài tại hai đỉnh A, C là:
Đáp án : A
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là: \(\widehat {{A_1}};\widehat {{B_1}};\widehat {{C_1}};\widehat {{D_1}}\) .
Khi đó ta có:
\(\begin{array}{l}\widehat A + \widehat {{A_1}} = {180^o} \Rightarrow \widehat {{A_1}} = {180^o} - \widehat A\\\widehat B + \widehat {{B_1}} = {180^o} \Rightarrow \widehat {{B_1}} = {180^o} - \widehat B\\\widehat C + \widehat {{C_1}} = {180^o} \Rightarrow \widehat {{C_1}} = {180^o} - \widehat C\\\widehat D + \widehat {{D_1}} = {180^o} \Rightarrow \widehat {{D_1}} = {180^o} - \widehat D\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = \left( {{{180}^o} - \widehat A} \right) + \left( {{{180}^o} - \widehat B} \right) + \left( {{{180}^o} - \widehat C} \right) + \left( {{{180}^o} - \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - {360^o} = {360^o}\end{array}\)
Vậy số đo 4 góc ngoài tứ giác tại 4 đỉnh A, B, C, D bằng \({360^o}\)
Mà tổng số đo góc ngoài hai đỉnh B, c bằng \({200^o}\) nên tổng số đo góc ngoài tại hai đỉnh A, D bằng \({360^o} - {200^0} = {160^o}\)
Tứ giác ABCD có AB = BC; CD = DA , \(\widehat B = {100^o};\widehat D = {70^o}\) . Tính \(\widehat A{,^{}}\widehat C\) ?
Đáp án : A
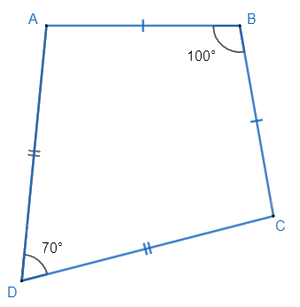
Xét tam giác ABC có AB = AC
\( \Rightarrow \Delta ABC\) cân tại B mà \(\widehat B = {100^o}\)
\( \Rightarrow \widehat {BAC} = \widehat {BCA} = \frac{{{{180}^o} - {{100}^o}}}{2} = {40^o}\)
Xét tam giác ADC có CD = DA
\( \Rightarrow \Delta A{{D}}C\) cân tại D có \(\widehat {A{{D}}C} = {70^o}\)
\( \Rightarrow \widehat {DAC} = \widehat {DCA} = \frac{{{{180}^o} - {{70}^o}}}{2} = {55^o}\)
Từ đó ta có:
\(\begin{array}{l}\widehat A = \widehat {BA{{D}}} = \widehat {BAC} + \widehat {CA{{D}}}\\ \Rightarrow \widehat A = \widehat {BA{{D}}} = {40^o} + {55^o} = {95^o}\end{array}\)
Và: \(\begin{array}{l}\widehat C = \widehat {BC{{D}}} = \widehat {BCA} + \widehat {AC{{D}}}\\ \Rightarrow \widehat C = \widehat {BC{{D}}} = {40^o} + {55^o} = {95^o}\end{array}\)
Vậy: \(\widehat A = \widehat C = {95^o}\)
Tam giác ABC có Â = 600, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc \(\widehat {BIC}{;^{}}\widehat {BKC}\)
Đáp án : D
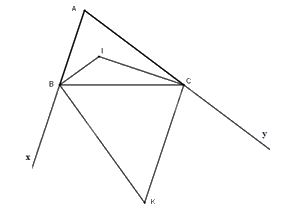
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat {ABC} + \widehat {BCA} = {180^o}\\ \Rightarrow \widehat {ABC} + \widehat {BCA} = {120^o}\end{array}\)
Vì BI là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \frac{1}{2}\widehat {BAC}\)
Vì CI là phân giác \(\widehat {BCA} \Rightarrow \widehat {BCI} = \frac{1}{2}\widehat {BCA}\)
Từ đó:
\(\widehat {CBI} + \widehat {BCI} = \frac{1}{2}\left( {\widehat {BAC} + \widehat {BCA}} \right) = \frac{1}{2}{.120^o} = {60^o}\)
Xét tam giác BCI có:
\(\widehat {BCI} + \widehat {BIC} + \widehat {CBI} = {180^o}\)
Nên: \(\widehat {BIC} = {180^o} - \left( {\widehat {BCI} + \widehat {CBI}} \right) = {180^o} - {60^o} = {120^o}\)
Vì BI là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \frac{1}{2}\widehat {BAC}\)
Vì BK là phân giác \(\widehat {CB{{x}}} \Rightarrow \widehat {CBK} = \frac{1}{2}\widehat {CBx}\)
Suy ra:
\(\widehat {CBK} + \widehat {CBI} = \frac{1}{2}\left( {\widehat {CBx} + \widehat {ABC}} \right) = \frac{1}{2}{.180^o} = {90^o}\)
Hay \(\widehat {IBK} = {90^o}\)
Tương tự ta có: \(\widehat {ICK} = {90^o}\)
Xét tứ giác BICK có:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICK} + \widehat {BKC} = {360^o}\\ \Rightarrow \widehat {BKC} = {360^o} - {90^o} - {90^o} - {120^o} = {60^o}\end{array}\)
Vậy \(\widehat {BIC} = {120^o}{;^{}}\widehat {BKC} = {60^o}\)
Tứ giác ABCD có: \(\widehat A + \widehat C = {60^o}\) Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.
Đáp án : A
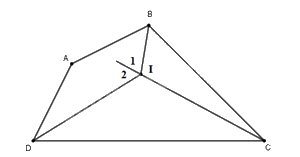
Xét tam giác BIC có:
\(\widehat {IBC} = \widehat {{I_1}} - \widehat {BCI}\)
Xét tam giác DIC có:
\(\widehat {I{{D}}C} = \widehat {{I_2}} - \widehat {IC{{D}}}\)
Nên: \(\widehat {IBC} + \widehat {I{{D}}C} = \left( {\widehat {{I_1}} + \widehat {{I_2}}} \right) - \left( {\widehat {{C_1}} + \widehat {{C_2}}} \right) = \widehat {BI{{D}}} - \widehat C\)
Tứ giác ABID:
\(\widehat {ABI} + \widehat {A{{D}}I} = {360^o} - \widehat A - \widehat {BI{{D}}}\)
Do: \(\widehat {ADI} = \widehat {I{{D}}C}\) (tính chất của tia phân giác)
Nên: \(\widehat {IBC} + \widehat {I{{D}}C} = \widehat {ABI} + \widehat {A{{D}}I}\)
Hay
\(\begin{array}{l}\widehat {BI{{D}}} - \widehat C = {360^o} - \widehat A - \widehat {BI{{D}}}\\ \Leftrightarrow 2\widehat {BI{{D}}} = {360^o} - \left( {\widehat A - \widehat C} \right) = {360^o} - {60^o} = {300^o}\end{array}\)
Suy ra: \(\widehat {BI{{D}}} = {150^o}\)
Hãy chọn câu sai trong các câu sau
Các góc của tứ giác có thể là
4 góc nhọn.
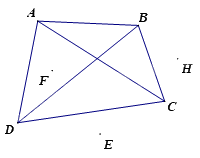
Cho hình vẽ dưới đây. Chọn khẳng định sai trong các câu sau

Chọn câu đúng trong các câu sau khi nói về định nghĩa tứ giác ABCD:
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA và 4 góc tại đỉnh bằng nhau.
Cho hình vẽ sau, chọn câu đúng:

Hai cạnh đối nhau: AB, BC.
Hai cạnh kề nhau: BC, DA.
Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
Điểm M nằm trong tứ giác ABCD và điểm N nằm ngoài tứ giác ABCD
Cho tứ giác ABCD trong đó: \(\widehat A + \widehat B = {140^o}\). Tổng \(\widehat C + \widehat D\) bằng:
Cho tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {117^o};\widehat C = {71^o}\). Số đo góc ngoài tại đỉnh D bằng:
Tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {123^o};\widehat D = {20^o}\). Số đo của góc C là:
Tứ giác ABCD có \(\widehat A = {100^o};\widehat B = {120^o};\widehat C - \widehat D = {20^o}\). Số đo các góc C, D là:
Tứ giác ABCD có các cạnh tỉ lệ với 3, 5, 7, 9 và chu vi là 240 m. Cạnh ngắn nhất là:
Cho tứ giác ABCD có góc ngoài tại đỉnh D bằng \({50^o}\) ; góc ngoài tại đỉnh A bằng \({100^o}\) . Tỉnh tổng \(\widehat A + \widehat D\) trong tứ giác ABCD là:
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng:
Cho tứ giác ABCD biết số đo của các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) tỉ lệ thuận với 4, 3, 5, 6. Khi đó số đo các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) lần lượt là:
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là:
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là \({200^o}\) . Tính số đo các góc ngoài tại hai đỉnh A, C là:
Tứ giác ABCD có AB = BC; CD = DA , \(\widehat B = {100^o};\widehat D = {70^o}\) . Tính \(\widehat A{,^{}}\widehat C\) ?
Tam giác ABC có Â = 600, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc \(\widehat {BIC}{;^{}}\widehat {BKC}\)
Tứ giác ABCD có: \(\widehat A + \widehat C = {60^o}\) Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.
Hãy chọn câu sai trong các câu sau
Đáp án : B
Các góc của tứ giác có thể là
4 góc nhọn.
Đáp án : C
Các góc của tứ giác có thể là 4 góc vuông vì khi đó tổng các góc của tứ giác này bằng 360o.
Các trường hợp còn lại không thỏa mãn định lí tổng các góc trong tam giác.
Cho hình vẽ dưới đây. Chọn khẳng định sai trong các câu sau

Đáp án : D
Chọn câu đúng trong các câu sau khi nói về định nghĩa tứ giác ABCD:
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA và 4 góc tại đỉnh bằng nhau.
Đáp án : B
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
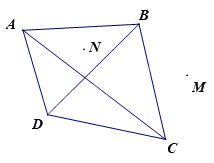
Cho hình vẽ sau, chọn câu đúng:

Hai cạnh đối nhau: AB, BC.
Hai cạnh kề nhau: BC, DA.
Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
Điểm M nằm trong tứ giác ABCD và điểm N nằm ngoài tứ giác ABCD
Đáp án : C
Từ hình vẽ ta thấy: Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
Cho tứ giác ABCD trong đó: \(\widehat A + \widehat B = {140^o}\). Tổng \(\widehat C + \widehat D\) bằng:
Đáp án : A
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\ \Rightarrow \widehat C + \widehat D = {360^o} - \left( {\widehat A + \widehat B} \right) = {360^o} - {140^o} = {220^o}\end{array}\)
Tổng các góc trong một tứ giác bằng \({360^o}\)
Cho tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {117^o};\widehat C = {71^o}\). Số đo góc ngoài tại đỉnh D bằng:
Đáp án : C
Tính góc D trong tứ giác ABCD. Từ đó góc ngoài tại đỉnh D bằng \({180^o}\) trừ đi góc D trong tứ giác ABCD.
Góc ngoài và góc trong tứ giác tại một đỉnh là hai góc kề bù.

\(\widehat {C{{D}}E}\) là góc ngoài đỉnh D. Tứ giác ABCD có:
\(\begin{array}{l}\widehat D = {360^o} - \left( {\widehat A + \widehat B + \widehat C} \right)\\\widehat D = {360^o} - \left( {{{50}^o} + {{117}^o} + {{71}^o}} \right)\\\widehat D = {122^o}\end{array}\)
Vì \(\widehat {A{{D}}C}\) và \(\widehat {C{{D}}E}\) là hai góc kề bù nên:
\(\widehat {C{{D}}E} = {180^o} - \widehat D = {180^o} - {122^o} = {58^o}\)
Tứ giác ABCD có \(\widehat A = {50^o};\widehat B = {123^o};\widehat D = {20^o}\). Số đo của góc C là:
Đáp án : B
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\ \Rightarrow \widehat C = {360^o} - \widehat A - \widehat B - \widehat D = {360^o} - {50^o} - {123^o} - {20^o} = {167^o}\end{array}\)
Tứ giác ABCD có \(\widehat A = {100^o};\widehat B = {120^o};\widehat C - \widehat D = {20^o}\). Số đo các góc C, D là:
Đáp án : C
Trong tứ giác ABCD ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Suy ra \(\widehat C + \widehat D = {360^o} - \widehat A - \widehat B = {360^o} - {100^o} - {120^o} = {140^o}(1)\)
Mà \(\widehat C - \widehat D = {20^o}\)(2)
Từ (1), (2) suy ra: \(\widehat C = \frac{140^o + 20^o}{2} = {80^o};\widehat D = \frac{140^o - 20^o}{2} = {60^o}\).
Tứ giác ABCD có các cạnh tỉ lệ với 3, 5, 7, 9 và chu vi là 240 m. Cạnh ngắn nhất là:
Đáp án : D
Gọi các cạnh AB, BC, CD, DA theo tỉ lệ 3, 5, 7, 9 nên ta có:
\(\frac{{AB}}{3} = \frac{{BC}}{5} = \frac{{C{{D}}}}{7} = \frac{{DA}}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{AB}}{3} = \frac{{BC}}{5} = \frac{{C{{D}}}}{7} = \frac{{DA}}{9} = \frac{{AB + BC + C{{D}} + DA}}{{3 + 5 + 7 + 9}} = \frac{{240}}{{24}} = 10\)
Suy ra: AB = 3. 10 = 30 cm
BC = 5 .10 = 50 cm
CD = 7. 10 = 70 cm
DA = 9 .10 = 90 cm
Vậy cạnh ngắn nhất là canh AB có độ dài 30 cm
Cho tứ giác ABCD có góc ngoài tại đỉnh D bằng \({50^o}\) ; góc ngoài tại đỉnh A bằng \({100^o}\) . Tỉnh tổng \(\widehat A + \widehat D\) trong tứ giác ABCD là:
Đáp án : D
Tổng hai góc trong và góc ngoài tại một đỉnh của tứ giác bằng \({180^o}\)
Vì góc ngoài đỉnh D bằng \({50^o}\) nên góc trong tại đỉnh D là: \(\widehat D = {180^o} - {50^o} = {130^o}\)
Vì góc ngoài tại đỉnh A bằng \({100^o}\) nên góc trong tại đỉnh A là: \(\widehat A = {180^o} - {100^o} = {80^o}\)
Suy ra: \(\widehat A + \widehat D = {80^o} + {130^o} = {210^o}\)
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng:
Đáp án : A

Xét tam giác ABC:
\(AB + BC > AC\) (bất đẳng thức tam giác)
Tương tự, lần lượt các tam giác BCD, CDA, DAB ta có:
\(\begin{array}{l}BC + C{{D}} > B{{D}}\\C{{D}} + DA > CA\\DA + AB > DB\end{array}\)
Cộng vế với vế ta được các bất đẳng thức trên ta được:
\(\begin{array}{l}AB + BC + C{{D}} + C{{D}} + DA + DA + AB > AC + B{{D}} + CA + DB\\ \Leftrightarrow 2\left( {AB + BC + C{{D}} + DA} \right) > 2\left( {AC + B{{D}}} \right)\\ \Leftrightarrow AB + BC + C{{D}} + DA > AC + B{{D}}\end{array}\)
Mà: \(AC + B{{D}} = OA + OC + OB + O{{D}}\) (hệ thức cộng đoạn thẳng)
\( \Leftrightarrow OA + OB + OC + O{{D}} < AB + BC + C{{D}} + DA\)
Vậy ta có: \(OA + OB + OC + O{{D}} < AB + BC + C{{D}} + DA\)
Cho tứ giác ABCD biết số đo của các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) tỉ lệ thuận với 4, 3, 5, 6. Khi đó số đo các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) lần lượt là:
Đáp án : A
\(\frac{{\widehat A}}{4} = \frac{{\widehat B}}{3} = \frac{{\widehat C}}{5} = \frac{{\widehat D}}{6} = \frac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{18}} = \frac{{{{360}^o}}}{{18}} = {20^o}\)
Do đó:
\(\begin{array}{l}\widehat A = {20^o}.4 = {80^o}\\\widehat B = {20^o}.3 = {60^o}\\\widehat C = {20^o}.5 = {100^o}\\\widehat D = {20^o}.6 = {120^o}\end{array}\)
Nên số đo các góc \(\widehat A,\widehat B,\widehat C,\widehat D\) lần lượt là \({80^o}{;^{}}{60^o}{;^{}}{100^o}{;^{}}{120^o}\)
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
Đáp án : B
Sử dụng định lí Pytago trong tam giác vuông.

Gọi K là giao điểm AD, BC.
Vì \(\widehat C + \widehat D = {90^o}\) nên \(\widehat K = {90^o}\)
Áp dụng định lí Pytago trong tam giác vuông vào các tam giác:
+ ΔKAC vuông tại K ta có: AC2 = KC2 + KA2.
+ ΔKBD vuông tại K ta có: BD2 = KB2 + KD2.
+ ΔKBA vuông tại K ta có: BA2 = KA2 + KB2.
+ ΔKBD vuông tại K ta có: CD2 = KC2 + KD2.
Từ đó AC2+ BD2 = KC2 + KA2 + KB2 + KD2
= (KB2 +KA2) + (KD2 + KC2) = AB2 + DC2.
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là:
Đáp án : D

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là: \(\widehat {{A_1}};\widehat {{B_1}};\widehat {{C_1}};\widehat {{D_1}}\) .
Khi đó ta có:
\(\begin{array}{l}\widehat A + \widehat {{A_1}} = {180^o} \Rightarrow \widehat {{A_1}} = {180^o} - \widehat A\\\widehat B + \widehat {{B_1}} = {180^o} \Rightarrow \widehat {{B_1}} = {180^o} - \widehat B\\\widehat C + \widehat {{C_1}} = {180^o} \Rightarrow \widehat {{C_1}} = {180^o} - \widehat C\\\widehat D + \widehat {{D_1}} = {180^o} \Rightarrow \widehat {{D_1}} = {180^o} - \widehat D\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = \left( {{{180}^o} - \widehat A} \right) + \left( {{{180}^o} - \widehat B} \right) + \left( {{{180}^o} - \widehat C} \right) + \left( {{{180}^o} - \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - {360^o} = {360^o}\end{array}\)
Vậy số đo 4 góc ngoài tứ giác tại 4 đỉnh A, B, C, D bằng \({360^o}\)
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là \({200^o}\) . Tính số đo các góc ngoài tại hai đỉnh A, C là:
Đáp án : A

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là: \(\widehat {{A_1}};\widehat {{B_1}};\widehat {{C_1}};\widehat {{D_1}}\) .
Khi đó ta có:
\(\begin{array}{l}\widehat A + \widehat {{A_1}} = {180^o} \Rightarrow \widehat {{A_1}} = {180^o} - \widehat A\\\widehat B + \widehat {{B_1}} = {180^o} \Rightarrow \widehat {{B_1}} = {180^o} - \widehat B\\\widehat C + \widehat {{C_1}} = {180^o} \Rightarrow \widehat {{C_1}} = {180^o} - \widehat C\\\widehat D + \widehat {{D_1}} = {180^o} \Rightarrow \widehat {{D_1}} = {180^o} - \widehat D\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = \left( {{{180}^o} - \widehat A} \right) + \left( {{{180}^o} - \widehat B} \right) + \left( {{{180}^o} - \widehat C} \right) + \left( {{{180}^o} - \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right)\\\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = {720^o} - {360^o} = {360^o}\end{array}\)
Vậy số đo 4 góc ngoài tứ giác tại 4 đỉnh A, B, C, D bằng \({360^o}\)
Mà tổng số đo góc ngoài hai đỉnh B, c bằng \({200^o}\) nên tổng số đo góc ngoài tại hai đỉnh A, D bằng \({360^o} - {200^0} = {160^o}\)
Tứ giác ABCD có AB = BC; CD = DA , \(\widehat B = {100^o};\widehat D = {70^o}\) . Tính \(\widehat A{,^{}}\widehat C\) ?
Đáp án : A

Xét tam giác ABC có AB = AC
\( \Rightarrow \Delta ABC\) cân tại B mà \(\widehat B = {100^o}\)
\( \Rightarrow \widehat {BAC} = \widehat {BCA} = \frac{{{{180}^o} - {{100}^o}}}{2} = {40^o}\)
Xét tam giác ADC có CD = DA
\( \Rightarrow \Delta A{{D}}C\) cân tại D có \(\widehat {A{{D}}C} = {70^o}\)
\( \Rightarrow \widehat {DAC} = \widehat {DCA} = \frac{{{{180}^o} - {{70}^o}}}{2} = {55^o}\)
Từ đó ta có:
\(\begin{array}{l}\widehat A = \widehat {BA{{D}}} = \widehat {BAC} + \widehat {CA{{D}}}\\ \Rightarrow \widehat A = \widehat {BA{{D}}} = {40^o} + {55^o} = {95^o}\end{array}\)
Và: \(\begin{array}{l}\widehat C = \widehat {BC{{D}}} = \widehat {BCA} + \widehat {AC{{D}}}\\ \Rightarrow \widehat C = \widehat {BC{{D}}} = {40^o} + {55^o} = {95^o}\end{array}\)
Vậy: \(\widehat A = \widehat C = {95^o}\)
Tam giác ABC có Â = 600, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc \(\widehat {BIC}{;^{}}\widehat {BKC}\)
Đáp án : D

Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat {ABC} + \widehat {BCA} = {180^o}\\ \Rightarrow \widehat {ABC} + \widehat {BCA} = {120^o}\end{array}\)
Vì BI là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \frac{1}{2}\widehat {BAC}\)
Vì CI là phân giác \(\widehat {BCA} \Rightarrow \widehat {BCI} = \frac{1}{2}\widehat {BCA}\)
Từ đó:
\(\widehat {CBI} + \widehat {BCI} = \frac{1}{2}\left( {\widehat {BAC} + \widehat {BCA}} \right) = \frac{1}{2}{.120^o} = {60^o}\)
Xét tam giác BCI có:
\(\widehat {BCI} + \widehat {BIC} + \widehat {CBI} = {180^o}\)
Nên: \(\widehat {BIC} = {180^o} - \left( {\widehat {BCI} + \widehat {CBI}} \right) = {180^o} - {60^o} = {120^o}\)
Vì BI là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \frac{1}{2}\widehat {BAC}\)
Vì BK là phân giác \(\widehat {CB{{x}}} \Rightarrow \widehat {CBK} = \frac{1}{2}\widehat {CBx}\)
Suy ra:
\(\widehat {CBK} + \widehat {CBI} = \frac{1}{2}\left( {\widehat {CBx} + \widehat {ABC}} \right) = \frac{1}{2}{.180^o} = {90^o}\)
Hay \(\widehat {IBK} = {90^o}\)
Tương tự ta có: \(\widehat {ICK} = {90^o}\)
Xét tứ giác BICK có:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICK} + \widehat {BKC} = {360^o}\\ \Rightarrow \widehat {BKC} = {360^o} - {90^o} - {90^o} - {120^o} = {60^o}\end{array}\)
Vậy \(\widehat {BIC} = {120^o}{;^{}}\widehat {BKC} = {60^o}\)
Tứ giác ABCD có: \(\widehat A + \widehat C = {60^o}\) Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.
Đáp án : A

Xét tam giác BIC có:
\(\widehat {IBC} = \widehat {{I_1}} - \widehat {BCI}\)
Xét tam giác DIC có:
\(\widehat {I{{D}}C} = \widehat {{I_2}} - \widehat {IC{{D}}}\)
Nên: \(\widehat {IBC} + \widehat {I{{D}}C} = \left( {\widehat {{I_1}} + \widehat {{I_2}}} \right) - \left( {\widehat {{C_1}} + \widehat {{C_2}}} \right) = \widehat {BI{{D}}} - \widehat C\)
Tứ giác ABID:
\(\widehat {ABI} + \widehat {A{{D}}I} = {360^o} - \widehat A - \widehat {BI{{D}}}\)
Do: \(\widehat {ADI} = \widehat {I{{D}}C}\) (tính chất của tia phân giác)
Nên: \(\widehat {IBC} + \widehat {I{{D}}C} = \widehat {ABI} + \widehat {A{{D}}I}\)
Hay
\(\begin{array}{l}\widehat {BI{{D}}} - \widehat C = {360^o} - \widehat A - \widehat {BI{{D}}}\\ \Leftrightarrow 2\widehat {BI{{D}}} = {360^o} - \left( {\widehat A - \widehat C} \right) = {360^o} - {60^o} = {300^o}\end{array}\)
Suy ra: \(\widehat {BI{{D}}} = {150^o}\)
Bài 2 trong chương trình Toán 8 Chân trời sáng tạo tập trung vào việc tìm hiểu về khái niệm tứ giác, các loại tứ giác đặc biệt (hình bình hành, hình chữ nhật, hình thoi, hình vuông), và các tính chất liên quan đến chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học phức tạp hơn trong các lớp học tiếp theo.
Các bài tập trắc nghiệm về tứ giác thường xoay quanh các chủ đề sau:
Để xác định loại tứ giác, bạn cần phân tích các yếu tố đã cho trong đề bài và so sánh với các dấu hiệu nhận biết của từng loại tứ giác. Ví dụ:
Khi giải các bài tập về tính chất của tứ giác, bạn cần vận dụng các định lý và tính chất đã học để tìm ra mối liên hệ giữa các yếu tố của tứ giác. Ví dụ:
Trong hình bình hành, hai cạnh đối song song và bằng nhau, hai góc đối bằng nhau, và hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Các bài tập ứng dụng thường yêu cầu bạn sử dụng kiến thức về tứ giác để giải quyết các bài toán thực tế. Ví dụ, tính chiều dài đường chéo của một hình chữ nhật, hoặc tính góc giữa hai đường chéo của một hình thoi.
Để nắm vững kiến thức về tứ giác, bạn nên luyện tập thường xuyên với các bài tập trắc nghiệm. Giaitoan.edu.vn cung cấp một bộ đề trắc nghiệm đa dạng, bao gồm các câu hỏi từ dễ đến khó, giúp bạn tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học tốt về tứ giác:
Trắc nghiệm Bài 2: Tứ giác Toán 8 Chân trời sáng tạo là một phần quan trọng trong chương trình học Toán 8. Việc nắm vững kiến thức về tứ giác sẽ giúp bạn tự tin giải quyết các bài toán hình học và đạt kết quả tốt trong các kỳ thi. Hãy luyện tập thường xuyên và sử dụng các tài liệu tham khảo hữu ích để nâng cao kiến thức của mình.