Chào mừng bạn đến với bài kiểm tra trắc nghiệm về chủ đề Hình thang và Hình thang cân trong chương trình Toán 8 Chân trời sáng tạo. Bài tập này được thiết kế để giúp bạn củng cố kiến thức đã học và rèn luyện kỹ năng giải bài tập một cách hiệu quả.
Giaitoan.edu.vn cung cấp bộ câu hỏi trắc nghiệm đa dạng, bao gồm các dạng bài tập từ cơ bản đến nâng cao, kèm theo đáp án chi tiết và lời giải thích rõ ràng.
Trong các khẳng định sau, khẳng định nào sai?
Hình thang cân là hình thang có
Số trục đối xứng của hình thang cân là
Tứ giác ABCD là hình thang vì có
Tứ giác ABCD có AB // CD là một hình thang, ta gọi
Trong các tứ giác sau,tứ giác nào là hình thang?
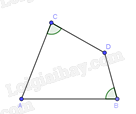 .
. 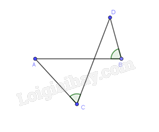 .
. 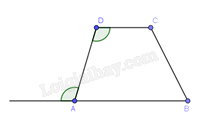 .
. 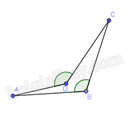 .
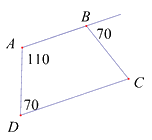
. Cho hình vẽ, số đo \(\widehat {BC{{D}}}\) bằng:
Cho hình thang cân ABCD có AB // CD và AC = 12 cm, AB = 6 cm. Tình BD
Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AD và BC. Tam giác MCD là tam giác gì:
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:
Cho hình thang ABCD (AB // CD) ta có:
Hình thang cân có một góc bằng \({50^o}\) . Hiệu giữa hai góc kề một cạnh bên là:
Cho hình thang ABCD (AB //CD) biết \(\widehat A = {58^o}\) thì:
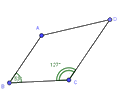
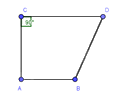
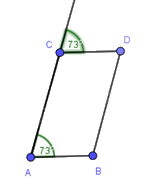
Tứ giác nào sau đây không phải hình thang:
 .
.  .
.  .
.  .
. Trong hình thang có hai góc tù:
hai góc còn lại gồm một góc tù và một góc nhọn
Cho hình vẽ sau. Biết ABCD là hình thang cân (AB // CD).
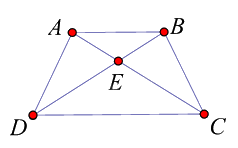
Tìm khẳng định đúng trong các khẳng định sau:
\(\Delta ABC = \Delta BDA\)
Cho tam giác ABC. Các điểm D và E lần lượt trên các cạnh AB, AC sao cho
DE // BC. Tứ giác DBEC là hình thang cân nếu:
Tam giác ABC vuông tại A.
Tam giác ABC cân tại C.
Tam giác ABC cân tại B.
Tam giác ABC cân tại A.
Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao
AH = 5 cm. Biết \(\widehat D = {45^o}\) . Độ dài đáy lớn CD là:
Cho hình thang cân ABCD có đáy nhỏ AB = 12cm., đáy lớn CD = 22 cm, cạnh bên BC = 13 cm thì đường cao AH bằng:
Cho hình vẽ sau, tính các góc A, C của hình thang ABCD (AB // CD) biết:
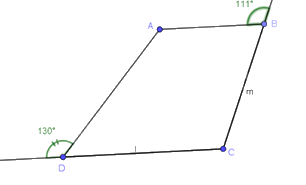
Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M thì
Hình thang ABCD (AB // CD) biết \(\widehat A - \widehat D = {40^o},\widehat B = 3\widehat C\) . Các góc của hình thang là:
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD có:
Cho hình thang cân ABCD (AB // CD). Giả sử \(AB \le C{{D}}\) . Tìm khẳng định đúng:
Lời giải và đáp án
Trong các khẳng định sau, khẳng định nào sai?
Đáp án : A
Dựa vào tính chất hình thang cân: Tứ giác có hai cạnh bên bằng nhau là hình thang cân là khẳng định sai, vì tứ giác có hai cạnh bên bằng nhau có thể là hình bình hành.
Hình thang cân là hình thang có
Đáp án : D
Số trục đối xứng của hình thang cân là
Đáp án : B
Tứ giác ABCD là hình thang vì có
Đáp án : A
Tứ giác ABCD có AB // CD là một hình thang, ta gọi
Đáp án : B
Trong các tứ giác sau,tứ giác nào là hình thang?
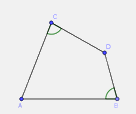 .
. 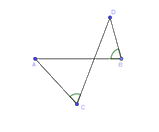 .
.  .
.  .
. Đáp án : C
Vậy tứ giác ABCD là hình thang
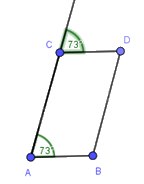
Cho hình vẽ, số đo \(\widehat {BC{{D}}}\) bằng:
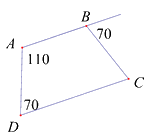
Đáp án : A
Tứ giác ABCD có \(\widehat A + \widehat D = {110^o} + {70^o} = {180^o}\) nên AB // CD suy ra ABCD là hình thang.
Mặt khác ta có: \(\widehat {ABC} = {180^o} - {70^o} = {110^o}\)
Hình thang ABCD có \(\widehat A = \widehat B = {110^o}\) . Suy ra ABCD là hình thang cân
Suy ra: \(\widehat C = \widehat D = {70^o}\)
Cho hình thang cân ABCD có AB // CD và AC = 12 cm, AB = 6 cm. Tình BD
Đáp án : A
Hình thang cân có hai đường chéo bằng nhau.
Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AD và BC. Tam giác MCD là tam giác gì:
Đáp án : A
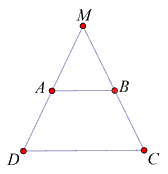
Vì ABCD là hình thang cân có hai đáy là AB và CD nên \(\widehat C = \widehat D\)
Mặt khác xét tam giác MCD có \(\widehat C = \widehat D\) . Suy ra tam giác MCD là tam giác cân.
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:
Đáp án : D
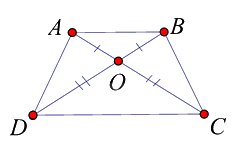
Ta có: \(OA = OB;OC = O{{D}} \Rightarrow OA + OC = OB + O{{D}} \Rightarrow AC = B{{D}}\)
Hình thang ABCD (AB //CD) có AC = BD nên ABCD là hình thang cân
Suy ra: BC = AD
Cho hình thang ABCD (AB // CD) ta có:
Đáp án : A
Hình thang ABCD có AB // CD thì \(\widehat A\) và \(\widehat D\) ; \(\widehat B\) và \(\widehat C\) là các cặp góc trong cùng phía nên \(\widehat A + \widehat D = {180^o};\widehat B + \widehat D = {180^o}\)
Hình thang cân có một góc bằng \({50^o}\) . Hiệu giữa hai góc kề một cạnh bên là:
Đáp án : C
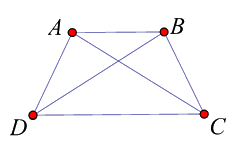
Giả sử ABCD là hình thang có đáy lớn là DC; đáy nhỏ là AB; \(\widehat C = \widehat D = {50^o}\) . Khi đó:
\(\widehat A = \widehat B = \frac{{{{360}^o} - \widehat C - \widehat D}}{2} = \frac{{{{360}^o} - {{50}^o} - {{50}^o}}}{2} = {130^o}\)
\( \Rightarrow \widehat B - \widehat C = \widehat A - \widehat D = {130^o} - {50^o} = {80^o}\)
Cho hình thang ABCD (AB //CD) biết \(\widehat A = {58^o}\) thì:
Đáp án : A
Mà \(\widehat A = {58^o}\) nên \({58^o} + \widehat D = {180^o} \Rightarrow \widehat D = {180^o} - {58^o} = {122^o}\)
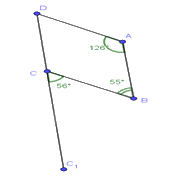
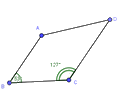
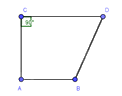
Tứ giác nào sau đây không phải hình thang:
 .
.  .
.  .
. 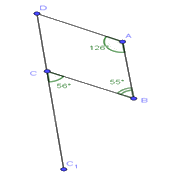 .
. Đáp án : D
Ta có: \(\widehat A + \widehat B = {126^o} + {55^o} = {181^o}\) nên Bc và AD không song song
Lại có: \(\widehat B \ne \widehat {BC{C_1}}\) nên AB và CD không song song với nhau
Vậy tứ giác ABCD ở hình D không phải là hình thang.
Trong hình thang có hai góc tù:
hai góc còn lại gồm một góc tù và một góc nhọn
Đáp án : D
Xét hình thang ABCD có AB // CD nên \(\widehat A + \widehat D = {180^o}\) (2 góc trong cùng phía) suy ra hai góc đó có nhiều nhất một góc nhọn, có nhiều nhất một góc tù.
Tương tự \(\widehat B\) và \(\widehat C\) cũng vậy.
Do đó trong bốn góc A, B, C, D có hai góc tù thì hai góc còn lại là hai góc nhọn.
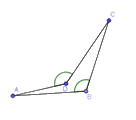
Cho hình vẽ sau. Biết ABCD là hình thang cân (AB // CD).
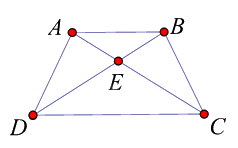
Tìm khẳng định đúng trong các khẳng định sau:
\(\Delta ABC = \Delta BDA\)
Đáp án : C
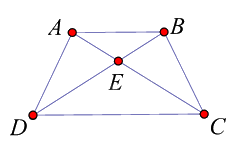
Xét tam giác ABC và tam giác BAD có:
AB là cạnh chung
\(\widehat {ABC} = \widehat {BAC}\) (hai góc kề một đáy của hình thang cân)
BC = AD (hai cạnh bên của hình thang cân)
Suy ra: \(\Delta ABC = \Delta BA{{D}}\) (c – g – c). Suy ra: \(\widehat {CAB} = \widehat {DBA}\) (hai góc tương ứng)
Tam giác ABE có \(\widehat {E{{A}}B} = \widehat {EBA}\) nên suy ra tam giác ABE là tam giác cân.
Cho tam giác ABC. Các điểm D và E lần lượt trên các cạnh AB, AC sao cho
DE // BC. Tứ giác DBEC là hình thang cân nếu:
Tam giác ABC vuông tại A.
Tam giác ABC cân tại C.
Tam giác ABC cân tại B.
Tam giác ABC cân tại A.
Đáp án : D
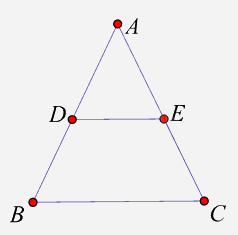
Tứ giác BDEC có DE // BC nên BDEC là hình thang . Để BDEC là hình thang cân thì \(\widehat B = \widehat C\) nên suy ra ABC là tam giác cân tại A.
Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao
AH = 5 cm. Biết \(\widehat D = {45^o}\) . Độ dài đáy lớn CD là:
Đáp án : D
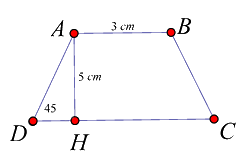
Ta có tam giác AHD vuông cân tại H vì \(\widehat D = {45^o}\) . Do đó DH = AH = 5 cm
Mà CD = AB + 2DH \( \Rightarrow C{{D}} = 3 + 2.5 = 13cm\)
Cho hình thang cân ABCD có đáy nhỏ AB = 12cm., đáy lớn CD = 22 cm, cạnh bên BC = 13 cm thì đường cao AH bằng:
Đáp án : D
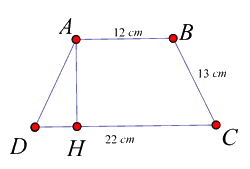
Xét hình thang cân ABCD có đáy lớn CD và đáy nhỏ AB đường cao AH ta có:
\(C{{D}} = AB + 2.DH \Rightarrow DH = \frac{{C{{D}} - AB}}{2} \Rightarrow DH = \frac{{22 - 12}}{2} = 5cm\)
Áp dụng định lí Pythago cho tam giác AHD vuông tại H có AD = BC = 13 cm và
DH = 5 cm ta có:
\(A{H^2} = A{{{D}}^2} - D{H^2} = {13^2} - {5^2} = 144 \Rightarrow AH = \sqrt {144} = 12cm\)
Cho hình vẽ sau, tính các góc A, C của hình thang ABCD (AB // CD) biết:
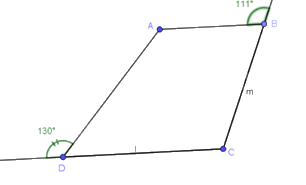
Đáp án : D
Hình thang ABCD có AB // CD nên \(\widehat A = \widehat {A{{D}}E} = {130^o};\widehat C = \widehat {ABF} = {111^o}\)
Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M thì
Đáp án : C
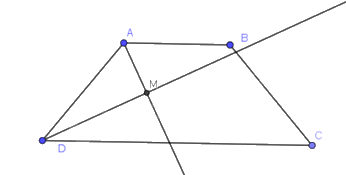
Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M nên
\(\widehat {DAM} + \widehat {ADM} = \frac{1}{2}\left( {\widehat A + \widehat D} \right) = \frac{1}{2}{.180^o} = {90^o}\)
Vậy \(\widehat {AM{{D}}} = {90^o}\)
Hình thang ABCD (AB // CD) biết \(\widehat A - \widehat D = {40^o},\widehat B = 3\widehat C\) . Các góc của hình thang là:
Đáp án : B
Hình thang ABCD (AB // CD) có \(\widehat A + \widehat D = {180^o}\) mà \(\widehat A - \widehat D = {40^o}\)
\( \Rightarrow \widehat A = {220^o}:2 = {110^o}\)
Do đó: \(\widehat D = {180^o} - {110^o} = {70^o}\)
Lại có: \(\widehat B + \widehat C = {180^o}\) (2 góc trong cùng phía) mà \(\widehat B = 3\widehat C\) nên
\(4\widehat C = {180^o} \Rightarrow \widehat C = {180^o}:4 = {45^o}\)
Suy ra: \(\widehat B = 3\widehat C = {3.45^o} = {135^o}\)
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD có:
Đáp án : D
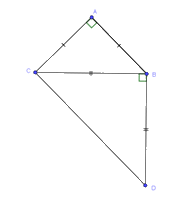
Xét tam giác BCD vuông cân tại B có \(\widehat {BC{{D}}} = \widehat {B{{D}}C} = {45^o}\) (2)
Từ (10, (2) suy ra: \(\widehat {ACB} + \widehat {BC{{D}}} = {90^o} = \widehat {AC{{D}}}\)
Cho hình thang cân ABCD (AB // CD). Giả sử \(AB \le C{{D}}\) . Tìm khẳng định đúng:
Đáp án : A
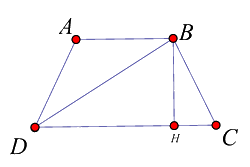
Kẻ \(BH \bot C{{D}}\) tại H.
Xét tam giác vuông BDH, theo định lý Pytago ta có: \(B{{{D}}^2} = D{H^2} + B{H^2}\)
Xét tam giác vuông CBH, theo định lý Pytago ta có: \(B{C^2} = C{H^2} + B{H^2}\)
Suy ra: \(B{{{D}}^2} - B{C^2} = D{H^2} - C{H^2} = \left( {DH + CH} \right)\left( {DH - CH} \right) = C{{D}}.AB\)
(Do DH + CH = CD; DH – CH = AB)
Trong các khẳng định sau, khẳng định nào sai?
Hình thang cân là hình thang có
Số trục đối xứng của hình thang cân là
Tứ giác ABCD là hình thang vì có
Tứ giác ABCD có AB // CD là một hình thang, ta gọi
Trong các tứ giác sau,tứ giác nào là hình thang?
 .
.  .
.  .
.  .
. Cho hình vẽ, số đo \(\widehat {BC{{D}}}\) bằng:

Cho hình thang cân ABCD có AB // CD và AC = 12 cm, AB = 6 cm. Tình BD
Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AD và BC. Tam giác MCD là tam giác gì:
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:
Cho hình thang ABCD (AB // CD) ta có:
Hình thang cân có một góc bằng \({50^o}\) . Hiệu giữa hai góc kề một cạnh bên là:
Cho hình thang ABCD (AB //CD) biết \(\widehat A = {58^o}\) thì:
Tứ giác nào sau đây không phải hình thang:
 .
.  .
.  .
.  .
. Trong hình thang có hai góc tù:
hai góc còn lại gồm một góc tù và một góc nhọn
Cho hình vẽ sau. Biết ABCD là hình thang cân (AB // CD).

Tìm khẳng định đúng trong các khẳng định sau:
\(\Delta ABC = \Delta BDA\)
Cho tam giác ABC. Các điểm D và E lần lượt trên các cạnh AB, AC sao cho
DE // BC. Tứ giác DBEC là hình thang cân nếu:
Tam giác ABC vuông tại A.
Tam giác ABC cân tại C.
Tam giác ABC cân tại B.
Tam giác ABC cân tại A.
Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao
AH = 5 cm. Biết \(\widehat D = {45^o}\) . Độ dài đáy lớn CD là:
Cho hình thang cân ABCD có đáy nhỏ AB = 12cm., đáy lớn CD = 22 cm, cạnh bên BC = 13 cm thì đường cao AH bằng:
Cho hình vẽ sau, tính các góc A, C của hình thang ABCD (AB // CD) biết:

Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M thì
Hình thang ABCD (AB // CD) biết \(\widehat A - \widehat D = {40^o},\widehat B = 3\widehat C\) . Các góc của hình thang là:
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD có:
Cho hình thang cân ABCD (AB // CD). Giả sử \(AB \le C{{D}}\) . Tìm khẳng định đúng:
Trong các khẳng định sau, khẳng định nào sai?
Đáp án : A
Dựa vào tính chất hình thang cân: Tứ giác có hai cạnh bên bằng nhau là hình thang cân là khẳng định sai, vì tứ giác có hai cạnh bên bằng nhau có thể là hình bình hành.
Hình thang cân là hình thang có
Đáp án : D
Số trục đối xứng của hình thang cân là
Đáp án : B
Tứ giác ABCD là hình thang vì có
Đáp án : A
Tứ giác ABCD có AB // CD là một hình thang, ta gọi
Đáp án : B
Trong các tứ giác sau,tứ giác nào là hình thang?
 .
.  .
.  .
.  .
. Đáp án : C
Vậy tứ giác ABCD là hình thang
Cho hình vẽ, số đo \(\widehat {BC{{D}}}\) bằng:

Đáp án : A
Tứ giác ABCD có \(\widehat A + \widehat D = {110^o} + {70^o} = {180^o}\) nên AB // CD suy ra ABCD là hình thang.
Mặt khác ta có: \(\widehat {ABC} = {180^o} - {70^o} = {110^o}\)
Hình thang ABCD có \(\widehat A = \widehat B = {110^o}\) . Suy ra ABCD là hình thang cân
Suy ra: \(\widehat C = \widehat D = {70^o}\)
Cho hình thang cân ABCD có AB // CD và AC = 12 cm, AB = 6 cm. Tình BD
Đáp án : A
Hình thang cân có hai đường chéo bằng nhau.
Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AD và BC. Tam giác MCD là tam giác gì:
Đáp án : A

Vì ABCD là hình thang cân có hai đáy là AB và CD nên \(\widehat C = \widehat D\)
Mặt khác xét tam giác MCD có \(\widehat C = \widehat D\) . Suy ra tam giác MCD là tam giác cân.
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:
Đáp án : D

Ta có: \(OA = OB;OC = O{{D}} \Rightarrow OA + OC = OB + O{{D}} \Rightarrow AC = B{{D}}\)
Hình thang ABCD (AB //CD) có AC = BD nên ABCD là hình thang cân
Suy ra: BC = AD
Cho hình thang ABCD (AB // CD) ta có:
Đáp án : A
Hình thang ABCD có AB // CD thì \(\widehat A\) và \(\widehat D\) ; \(\widehat B\) và \(\widehat C\) là các cặp góc trong cùng phía nên \(\widehat A + \widehat D = {180^o};\widehat B + \widehat D = {180^o}\)
Hình thang cân có một góc bằng \({50^o}\) . Hiệu giữa hai góc kề một cạnh bên là:
Đáp án : C

Giả sử ABCD là hình thang có đáy lớn là DC; đáy nhỏ là AB; \(\widehat C = \widehat D = {50^o}\) . Khi đó:
\(\widehat A = \widehat B = \frac{{{{360}^o} - \widehat C - \widehat D}}{2} = \frac{{{{360}^o} - {{50}^o} - {{50}^o}}}{2} = {130^o}\)
\( \Rightarrow \widehat B - \widehat C = \widehat A - \widehat D = {130^o} - {50^o} = {80^o}\)
Cho hình thang ABCD (AB //CD) biết \(\widehat A = {58^o}\) thì:
Đáp án : A
Mà \(\widehat A = {58^o}\) nên \({58^o} + \widehat D = {180^o} \Rightarrow \widehat D = {180^o} - {58^o} = {122^o}\)
Tứ giác nào sau đây không phải hình thang:
 .
.  .
.  .
.  .
. Đáp án : D
Ta có: \(\widehat A + \widehat B = {126^o} + {55^o} = {181^o}\) nên Bc và AD không song song
Lại có: \(\widehat B \ne \widehat {BC{C_1}}\) nên AB và CD không song song với nhau
Vậy tứ giác ABCD ở hình D không phải là hình thang.
Trong hình thang có hai góc tù:
hai góc còn lại gồm một góc tù và một góc nhọn
Đáp án : D

Xét hình thang ABCD có AB // CD nên \(\widehat A + \widehat D = {180^o}\) (2 góc trong cùng phía) suy ra hai góc đó có nhiều nhất một góc nhọn, có nhiều nhất một góc tù.
Tương tự \(\widehat B\) và \(\widehat C\) cũng vậy.
Do đó trong bốn góc A, B, C, D có hai góc tù thì hai góc còn lại là hai góc nhọn.
Cho hình vẽ sau. Biết ABCD là hình thang cân (AB // CD).

Tìm khẳng định đúng trong các khẳng định sau:
\(\Delta ABC = \Delta BDA\)
Đáp án : C

Xét tam giác ABC và tam giác BAD có:
AB là cạnh chung
\(\widehat {ABC} = \widehat {BAC}\) (hai góc kề một đáy của hình thang cân)
BC = AD (hai cạnh bên của hình thang cân)
Suy ra: \(\Delta ABC = \Delta BA{{D}}\) (c – g – c). Suy ra: \(\widehat {CAB} = \widehat {DBA}\) (hai góc tương ứng)
Tam giác ABE có \(\widehat {E{{A}}B} = \widehat {EBA}\) nên suy ra tam giác ABE là tam giác cân.
Cho tam giác ABC. Các điểm D và E lần lượt trên các cạnh AB, AC sao cho
DE // BC. Tứ giác DBEC là hình thang cân nếu:
Tam giác ABC vuông tại A.
Tam giác ABC cân tại C.
Tam giác ABC cân tại B.
Tam giác ABC cân tại A.
Đáp án : D

Tứ giác BDEC có DE // BC nên BDEC là hình thang . Để BDEC là hình thang cân thì \(\widehat B = \widehat C\) nên suy ra ABC là tam giác cân tại A.
Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao
AH = 5 cm. Biết \(\widehat D = {45^o}\) . Độ dài đáy lớn CD là:
Đáp án : D

Ta có tam giác AHD vuông cân tại H vì \(\widehat D = {45^o}\) . Do đó DH = AH = 5 cm
Mà CD = AB + 2DH \( \Rightarrow C{{D}} = 3 + 2.5 = 13cm\)
Cho hình thang cân ABCD có đáy nhỏ AB = 12cm., đáy lớn CD = 22 cm, cạnh bên BC = 13 cm thì đường cao AH bằng:
Đáp án : D

Xét hình thang cân ABCD có đáy lớn CD và đáy nhỏ AB đường cao AH ta có:
\(C{{D}} = AB + 2.DH \Rightarrow DH = \frac{{C{{D}} - AB}}{2} \Rightarrow DH = \frac{{22 - 12}}{2} = 5cm\)
Áp dụng định lí Pythago cho tam giác AHD vuông tại H có AD = BC = 13 cm và
DH = 5 cm ta có:
\(A{H^2} = A{{{D}}^2} - D{H^2} = {13^2} - {5^2} = 144 \Rightarrow AH = \sqrt {144} = 12cm\)
Cho hình vẽ sau, tính các góc A, C của hình thang ABCD (AB // CD) biết:

Đáp án : D
Hình thang ABCD có AB // CD nên \(\widehat A = \widehat {A{{D}}E} = {130^o};\widehat C = \widehat {ABF} = {111^o}\)
Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M thì
Đáp án : C

Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M nên
\(\widehat {DAM} + \widehat {ADM} = \frac{1}{2}\left( {\widehat A + \widehat D} \right) = \frac{1}{2}{.180^o} = {90^o}\)
Vậy \(\widehat {AM{{D}}} = {90^o}\)
Hình thang ABCD (AB // CD) biết \(\widehat A - \widehat D = {40^o},\widehat B = 3\widehat C\) . Các góc của hình thang là:
Đáp án : B
Hình thang ABCD (AB // CD) có \(\widehat A + \widehat D = {180^o}\) mà \(\widehat A - \widehat D = {40^o}\)
\( \Rightarrow \widehat A = {220^o}:2 = {110^o}\)
Do đó: \(\widehat D = {180^o} - {110^o} = {70^o}\)
Lại có: \(\widehat B + \widehat C = {180^o}\) (2 góc trong cùng phía) mà \(\widehat B = 3\widehat C\) nên
\(4\widehat C = {180^o} \Rightarrow \widehat C = {180^o}:4 = {45^o}\)
Suy ra: \(\widehat B = 3\widehat C = {3.45^o} = {135^o}\)
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD có:
Đáp án : D

Xét tam giác BCD vuông cân tại B có \(\widehat {BC{{D}}} = \widehat {B{{D}}C} = {45^o}\) (2)
Từ (10, (2) suy ra: \(\widehat {ACB} + \widehat {BC{{D}}} = {90^o} = \widehat {AC{{D}}}\)
Cho hình thang cân ABCD (AB // CD). Giả sử \(AB \le C{{D}}\) . Tìm khẳng định đúng:
Đáp án : A

Kẻ \(BH \bot C{{D}}\) tại H.
Xét tam giác vuông BDH, theo định lý Pytago ta có: \(B{{{D}}^2} = D{H^2} + B{H^2}\)
Xét tam giác vuông CBH, theo định lý Pytago ta có: \(B{C^2} = C{H^2} + B{H^2}\)
Suy ra: \(B{{{D}}^2} - B{C^2} = D{H^2} - C{H^2} = \left( {DH + CH} \right)\left( {DH - CH} \right) = C{{D}}.AB\)
(Do DH + CH = CD; DH – CH = AB)
Bài 3 trong chương trình Toán 8 Chân trời sáng tạo tập trung vào việc nghiên cứu về hình thang và hình thang cân. Đây là một phần quan trọng trong chương trình hình học, giúp học sinh hiểu rõ hơn về các tính chất, định nghĩa và ứng dụng của các loại hình thang đặc biệt này.
Hình thang là tứ giác có hai cạnh đối song song. Hai cạnh song song đó được gọi là đáy, còn hai cạnh còn lại là cạnh bên. Để nắm vững kiến thức về hình thang, bạn cần hiểu rõ các định nghĩa sau:
Các bài tập trắc nghiệm về hình thang và hình thang cân thường xoay quanh các chủ đề sau:
Để giải các bài tập trắc nghiệm về hình thang và hình thang cân một cách hiệu quả, bạn nên:
Câu 1: Cho hình thang ABCD có AB // CD, AB = 5cm, CD = 10cm. Gọi M là trung điểm của AD và N là trung điểm của BC. Độ dài MN bằng bao nhiêu?
A. 2.5cm
B. 5cm
C. 7.5cm
D. 10cm
Giải: MN là đường trung bình của hình thang ABCD, do đó MN = (AB + CD) / 2 = (5 + 10) / 2 = 7.5cm. Đáp án đúng là C.
Để nắm vững kiến thức về hình thang và hình thang cân, bạn nên luyện tập thường xuyên với các bài tập trắc nghiệm khác nhau. Giaitoan.edu.vn cung cấp một nguồn tài liệu phong phú và đa dạng để bạn có thể rèn luyện kỹ năng giải bài tập một cách hiệu quả.
Ngoài các kiến thức cơ bản về hình thang và hình thang cân, bạn có thể tìm hiểu thêm về các ứng dụng của chúng trong thực tế, ví dụ như trong kiến trúc, xây dựng, hoặc trong các lĩnh vực khoa học khác.
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về trắc nghiệm Bài 3: Hình thang - Hình thang cân Toán 8 Chân trời sáng tạo. Chúc bạn học tập tốt!