Chào mừng các em học sinh đến với bài trắc nghiệm Bài 1: Phương trình bậc nhất một ẩn môn Toán lớp 8, chương trình Chân trời sáng tạo. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức về phương trình bậc nhất một ẩn, một trong những kiến thức nền tảng quan trọng của chương trình Toán lớp 8.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, bao gồm nhiều dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp các em làm quen với các dạng đề thi và rèn luyện kỹ năng giải quyết vấn đề.
Phương trình với ẩn x có dạng:
Phương trình nào dưới đây là phương trình một ẩn?
\({x_0}\)được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\)nếu:
Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho được gọi là phương trình bậc nhất một ẩn x khi:
Cho phương trình \(2x + 1 = 0\), chọn khẳng định đúng
Nghiệm của phương trình \(3x - 6 = 0\) là:
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
Ở một số quốc gia, người ta dùng cả hai đơn vị đo nhiệt độ là Fahrenheit (oF) và độ Celcius (oC), liên hệ với nhau bởi công thức \(C = \frac{5}{9}\left( {F - 32} \right).\) Khi ở 20 oC thì ứng với độ Fahrenheit là:
Biết rằng \(4x - 8 = 0\). Giá trị của biểu thức \(5{x^2} - 4\) là:
Phương trình \({x^2} + 4 = 0\) có bao nhiêu nghiệm?
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
Hình tam giác và hình chữ nhật ở hình dưới có cùng chu vi. Khi đó, giá trị của x là:

Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
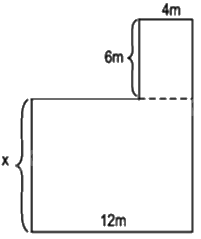
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
Số nghiệm của phương trình \(\sqrt x + 1 = 2\sqrt { - x} \) là:
Hình dưới dây mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1ft=0,3048m). Tốc độ v(ft/s) của nước tại thời điểm t(s) được cho bởi công thức \(v = 48 - 30t.\) Thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:

Lời giải và đáp án
Phương trình với ẩn x có dạng:
Đáp án : A
Phương trình nào dưới đây là phương trình một ẩn?
Đáp án : C
\(2{x^2} + 1 = x - 2\) là phương trình một ẩn (ẩn x)
Lưu ý: Đề bài chỉ hỏi phương trình một ẩn.
\({x_0}\)được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\)nếu:
Đáp án : D
Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho được gọi là phương trình bậc nhất một ẩn x khi:
Đáp án : C
Cho phương trình \(2x + 1 = 0\), chọn khẳng định đúng
Đáp án : A
Nghiệm của phương trình \(3x - 6 = 0\) là:
Đáp án : C
\(3x - 6 = 0\)
\(3x = 0 + 6\)
\(3x = 6\)
\(x = \frac{6}{3} \)
\(x = 2\)
Vậy phương trình có nghiệm \(x = 2\)
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
Đáp án : B
\(\frac{3}{4} + \frac{2}{5}x = 0\)
\(\frac{2}{5}x = \frac{{ - 3}}{4}\)
\(x = \frac{{ - 3}}{4}:\frac{2}{5} = \frac{{ - 15}}{8}\)
Do đó, \(a = 15,b = 8\)
Vậy \(a + b = 15 + 8 = 23\)
Ở một số quốc gia, người ta dùng cả hai đơn vị đo nhiệt độ là Fahrenheit (oF) và độ Celcius (oC), liên hệ với nhau bởi công thức \(C = \frac{5}{9}\left( {F - 32} \right).\) Khi ở 20 oC thì ứng với độ Fahrenheit là:
Đáp án : D
Với \(C = {20^o}C\) ta có:
\(20 = \frac{5}{9}\left( {F - 32} \right)\)
\(F - 32 = 20 : \frac{5}{9}\)
\(F - 32 = 36\)
\(F = 36 + 32 = 68\)
Vậy \(C = {20^o}C\) thì ứng với 68 oF
Biết rằng \(4x - 8 = 0\). Giá trị của biểu thức \(5{x^2} - 4\) là:
Đáp án : D
\(4x - 8 = 0\)
\(4x = 8\)
\(x = \frac{8}{4} = 2\)
Với \(x = 2\) thay vào biểu thức \(5{x^2} - 4\) ta có: \({5.2^2} - 4 = 16\)
Phương trình \({x^2} + 4 = 0\) có bao nhiêu nghiệm?
Đáp án : A
Vì \({x^2} \ge 0\) với mọi x nên \({x^2} + 4 > 0\) với mọi x.
Do đó, phương trình \({x^2} + 4 = 0\) vô nghiệm.
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
Đáp án : A
Theo đề bài ta có: \(\left( {x - \frac{1}{4}} \right).\frac{1}{2} = \frac{1}{8}\)
\(x - \frac{1}{4} = \frac{1}{8}:\frac{1}{2} = \frac{1}{4}\)
\(x = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\)
Vậy \(x = \frac{1}{2}\)
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
Đáp án : A
\(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}\)
\(3x - 15 + 9{x^2} - 27x = 9{x^2}\)
\( - 24x = 15\)
\(x = \frac{{ - 5}}{8}\)
Khi đó, nghiệm của phương là \({x_0} = \frac{{ - 5}}{8}\)
Do đó, \({x_0} < 0\)
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
Đáp án : B
Vì \(A = B\) nên \(\frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2} = \frac{{1 + 3x}}{4}\)
\(\frac{{8\left( {x + 1} \right)}}{{12}} - \frac{6}{{12}} = \frac{{3\left( {1 + 3x} \right)}}{{12}}\)
\(8x + 8 - 6 = 3 + 9x\)
\(9x - 8x = 2 - 3\)
\(x = - 1\)
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
Đáp án : C
\(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\)
\(8x - 16 = 14 + 6x - 6 + 2x + 10\)
\(8x - 6x - 2x = 18 + 16\)
\(0 = 34\) (vô lí)
Vậy phương trình (1) vô nghiệm.
\({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\)
\({x^2} - 4x + 4 = {x^2} - 2x - 2x + 4\)
\({x^2} - 4x + 4 - {x^2} + 4x - 4 = 0\)
\(0 = 0\) (luôn đúng)
Vậy phương trình (2) có vô số nghiệm.
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
Đáp án : B
\(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\)
\(\left( {\frac{{x - 11}}{{2011}} - 1} \right) + \left( {\frac{{x - 10}}{{2012}} - 1} \right) = \left( {\frac{{x - 74}}{{1948}} - 1} \right) + \left( {\frac{{x - 72}}{{1950}} - 1} \right)\)
\(\frac{{x - 2022}}{{2011}} + \frac{{x - 2022}}{{2012}} - \frac{{x - 2022}}{{1948}} - \frac{{x - 2022}}{{1950}} = 0\)
\(\left( {x - 2022} \right)\left( {\frac{1}{{2011}} + \frac{1}{{2012}} - \frac{1}{{1948}} - \frac{1}{{1950}}} \right) = 0\)
\(x - 2022 = 0\) (vì \(\frac{1}{{2011}} + \frac{1}{{2012}} - \frac{1}{{1948}} - \frac{1}{{1950}} < 0\))
\(x = 2022\)
Vì 2022 chia hết cho 2, không chia hết cho 4, không chia hết cho 5 nên nghiệm của phương trình là một số chia hết cho 2
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
Đáp án : A
+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng khái niệm phương trình bậc nhất một ẩn: Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho và \(a \ne 0\) được gọi là phương trình bậc nhất một ẩn x.
\(3mx + m - 4x = 3{m^2} + 1\)
\(\left( {3m - 4} \right)x + m - 3{m^2} - 1 = 0\)
Để phương trình \(\left( {3m - 4} \right)x + m - 3{m^2} - 1 = 0\) có nghiệm duy nhất thì \(3m - 4 \ne 0\)
\(3m \ne 4\)
\(m \ne \frac{4}{3}\)
Vậy \(m \ne \frac{4}{3}\)
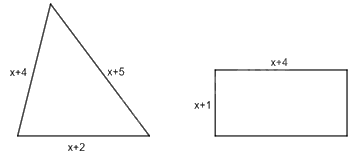
Hình tam giác và hình chữ nhật ở hình dưới có cùng chu vi. Khi đó, giá trị của x là:
Đáp án : C
+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng chu vi hình tam giác: Chu vi hình tam giác bằng tổng độ dài ba cạnh của tam giác
+ Sử dụng chu vi hình chữ nhật: Chu vi hình tam giác bằng hai lần tổng chiều dài và chiều rộng
Chu vi hình tam giác là: \(x + 2 + x + 4 + x + 5 = 3x + 11\)
Chu vi hình chữ nhật là: \(2\left( {x + 1 + x + 4} \right) = 2\left( {2x + 5} \right) = 4x + 10\)
Vì hai hình có chu vi bằng nhau nên: \(3x + 11 = 4x + 10\)
\(4x - 3x = 11 - 10\)
\(x = 1\)
Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
Đáp án : A
+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng khái niệm nghiệm của phương trình: Số \({x_0}\)được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\)nếu giá trị của A(x) và B(x) tại \({x_0}\)bằng nhau.
\(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\)
\(\frac{{21x}}{{24}} - \frac{{120\left( {x - 9} \right)}}{{24}} = \frac{{4\left( {20x + 1,5} \right)}}{{24}}\)
\(21x - 120x + 1080 = 80x + 6\)
\( - 179x = - 1074\)
\(x = 6\)
Vì phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) nên phương trình (2) có nghiệm là \(x = 2\)
\(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Với \(x = 2\) thay vào phương trình (2) ta có:
\(2\left( {a - 1} \right)2 - a\left( {2 - 1} \right) = 2a + 3\)
\(4a - 4 - a = 2a + 3\)
\(a = 7\)
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
Đáp án : D
\(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\)
\(\frac{{4\left( {x + 1} \right)}}{{12}} + \frac{{9\left( {2x + 1} \right)}}{{12}} = \frac{{2\left( {5x + 3} \right)}}{{12}} + \frac{{7 + 12x}}{{12}}\)
\(4x + 4 + 18x + 9 = 10x + 6 + 7 + 12x\)
\(22x + 13 = 22x + 13\)
\(0 = 0\) (luôn đúng)
Vậy phương trình đã cho có vô số nghiệm
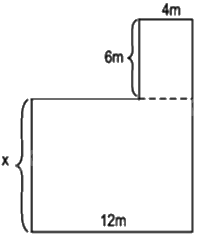
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:
Đáp án : B
Hình bên có gồm hai hình chữ nhật:
+ Hình chữ nhật độ dài 2 kích thước là 12m và x (mét) nên diện tích hình là: \(12x\left( {{m^2}} \right)\)
+ Hình chữ nhật có độ dài 2 kích thước là 6m và 4m nên diện tích hình là: \(4.6 = 24\left( {{m^2}} \right)\)
Mà diện tích của cả hình đó bằng \(168{m^2}\) nên ta có:
\(12x + 24 = 168\)
\(12x = 144\)
\(x = 12\)
Vậy \(x = 12m\)
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
Đáp án : D

Giả sử ô tô gặp xe máy tại C như trên hình.
Gọi x (giờ) (x > 0) là khoảng thời gian chuyển động của ôtô đi từ A đến C.
Ô tô đi với vận tốc 48km/h nên quãng đường AC bằng: 48.x (km) (1)
Vì xe máy đi trước ôtô 1 giờ nên thời gian xe máy đi từ A đến C bằng: x + 1 (h)
Xe máy đi với vận tốc 32km/h nên quãng đường AC bằng: 32(x + 1) (km) (2)
Từ (1) và (2) ta có phương trình: 48x = 32(x + 1).
Vậy phương trình là: 48x = 32(x + 1).
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
Đáp án : B
\(\left( {{m^2} - 3m + 2} \right)x = m - 2\left( * \right)\)
Xét \({m^2} - 3m + 2 = 0\)
\({m^2} - m - 2m + 2 = 0\)
\(\left( {m - 1} \right)\left( {m - 2} \right) = 0\)
Từ đó tính được \(m = 1;m = 2\)
Với \(m = 1\) thay vào (*) ta có: \(0.x = - 1\) (vô lí) nên phương trình (*) vô nghiệm.
Với \(m = 2\) thay vào (*) ta có: \(0x = 0\) (luôn đúng) nên phương trình (*) có vô số nghiệm với mọi số thực x.
Số nghiệm của phương trình \(\sqrt x + 1 = 2\sqrt { - x} \) là:
Đáp án : C
Khi \(x = 0\) ta có: \(1 = 0\) (vô lí) nên \(x = 0\) không là nghiệm của phương trình đã cho
Khi \(x < 0\) thì \(\sqrt x \) không xác định
Khi \(x > 0\) thì \(\sqrt { - x} \) không xác định
Vậy trong mọi trường hợp, không có giá trị nào thỏa mãn phương trình.
Vậy phương trình đã cho vô nghiệm
Hình dưới dây mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1ft=0,3048m). Tốc độ v(ft/s) của nước tại thời điểm t(s) được cho bởi công thức \(v = 48 - 30t.\) Thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:

Đáp án : C
Khi xuất phát từ mặt đài phun nước, giọt nước có \(t = 0.\)
Khi giọt nước đạt độ cao tối đa thì \(v = 0.\) Thay vào công thức ta có:
\(0 = 48 - 30t\)
\(30t = 48\)
\(t = 1,6\)
Vậy thời gian để giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là: \(1,6 - 0 = 1,6\) (s)
Phương trình với ẩn x có dạng:
Phương trình nào dưới đây là phương trình một ẩn?
\({x_0}\)được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\)nếu:
Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho được gọi là phương trình bậc nhất một ẩn x khi:
Cho phương trình \(2x + 1 = 0\), chọn khẳng định đúng
Nghiệm của phương trình \(3x - 6 = 0\) là:
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
Ở một số quốc gia, người ta dùng cả hai đơn vị đo nhiệt độ là Fahrenheit (oF) và độ Celcius (oC), liên hệ với nhau bởi công thức \(C = \frac{5}{9}\left( {F - 32} \right).\) Khi ở 20 oC thì ứng với độ Fahrenheit là:
Biết rằng \(4x - 8 = 0\). Giá trị của biểu thức \(5{x^2} - 4\) là:
Phương trình \({x^2} + 4 = 0\) có bao nhiêu nghiệm?
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
Hình tam giác và hình chữ nhật ở hình dưới có cùng chu vi. Khi đó, giá trị của x là:

Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:

Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
Số nghiệm của phương trình \(\sqrt x + 1 = 2\sqrt { - x} \) là:
Hình dưới dây mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1ft=0,3048m). Tốc độ v(ft/s) của nước tại thời điểm t(s) được cho bởi công thức \(v = 48 - 30t.\) Thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:

Phương trình với ẩn x có dạng:
Đáp án : A
Phương trình nào dưới đây là phương trình một ẩn?
Đáp án : C
\(2{x^2} + 1 = x - 2\) là phương trình một ẩn (ẩn x)
Lưu ý: Đề bài chỉ hỏi phương trình một ẩn.
\({x_0}\)được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\)nếu:
Đáp án : D
Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho được gọi là phương trình bậc nhất một ẩn x khi:
Đáp án : C
Cho phương trình \(2x + 1 = 0\), chọn khẳng định đúng
Đáp án : A
Nghiệm của phương trình \(3x - 6 = 0\) là:
Đáp án : C
\(3x - 6 = 0\)
\(3x = 0 + 6\)
\(3x = 6\)
\(x = \frac{6}{3} \)
\(x = 2\)
Vậy phương trình có nghiệm \(x = 2\)
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
Đáp án : B
\(\frac{3}{4} + \frac{2}{5}x = 0\)
\(\frac{2}{5}x = \frac{{ - 3}}{4}\)
\(x = \frac{{ - 3}}{4}:\frac{2}{5} = \frac{{ - 15}}{8}\)
Do đó, \(a = 15,b = 8\)
Vậy \(a + b = 15 + 8 = 23\)
Ở một số quốc gia, người ta dùng cả hai đơn vị đo nhiệt độ là Fahrenheit (oF) và độ Celcius (oC), liên hệ với nhau bởi công thức \(C = \frac{5}{9}\left( {F - 32} \right).\) Khi ở 20 oC thì ứng với độ Fahrenheit là:
Đáp án : D
Với \(C = {20^o}C\) ta có:
\(20 = \frac{5}{9}\left( {F - 32} \right)\)
\(F - 32 = 20 : \frac{5}{9}\)
\(F - 32 = 36\)
\(F = 36 + 32 = 68\)
Vậy \(C = {20^o}C\) thì ứng với 68 oF
Biết rằng \(4x - 8 = 0\). Giá trị của biểu thức \(5{x^2} - 4\) là:
Đáp án : D
\(4x - 8 = 0\)
\(4x = 8\)
\(x = \frac{8}{4} = 2\)
Với \(x = 2\) thay vào biểu thức \(5{x^2} - 4\) ta có: \({5.2^2} - 4 = 16\)
Phương trình \({x^2} + 4 = 0\) có bao nhiêu nghiệm?
Đáp án : A
Vì \({x^2} \ge 0\) với mọi x nên \({x^2} + 4 > 0\) với mọi x.
Do đó, phương trình \({x^2} + 4 = 0\) vô nghiệm.
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
Đáp án : A
Theo đề bài ta có: \(\left( {x - \frac{1}{4}} \right).\frac{1}{2} = \frac{1}{8}\)
\(x - \frac{1}{4} = \frac{1}{8}:\frac{1}{2} = \frac{1}{4}\)
\(x = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\)
Vậy \(x = \frac{1}{2}\)
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
Đáp án : A
\(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}\)
\(3x - 15 + 9{x^2} - 27x = 9{x^2}\)
\( - 24x = 15\)
\(x = \frac{{ - 5}}{8}\)
Khi đó, nghiệm của phương là \({x_0} = \frac{{ - 5}}{8}\)
Do đó, \({x_0} < 0\)
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
Đáp án : B
Vì \(A = B\) nên \(\frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2} = \frac{{1 + 3x}}{4}\)
\(\frac{{8\left( {x + 1} \right)}}{{12}} - \frac{6}{{12}} = \frac{{3\left( {1 + 3x} \right)}}{{12}}\)
\(8x + 8 - 6 = 3 + 9x\)
\(9x - 8x = 2 - 3\)
\(x = - 1\)
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
Đáp án : C
\(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\)
\(8x - 16 = 14 + 6x - 6 + 2x + 10\)
\(8x - 6x - 2x = 18 + 16\)
\(0 = 34\) (vô lí)
Vậy phương trình (1) vô nghiệm.
\({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\)
\({x^2} - 4x + 4 = {x^2} - 2x - 2x + 4\)
\({x^2} - 4x + 4 - {x^2} + 4x - 4 = 0\)
\(0 = 0\) (luôn đúng)
Vậy phương trình (2) có vô số nghiệm.
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
Đáp án : B
\(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\)
\(\left( {\frac{{x - 11}}{{2011}} - 1} \right) + \left( {\frac{{x - 10}}{{2012}} - 1} \right) = \left( {\frac{{x - 74}}{{1948}} - 1} \right) + \left( {\frac{{x - 72}}{{1950}} - 1} \right)\)
\(\frac{{x - 2022}}{{2011}} + \frac{{x - 2022}}{{2012}} - \frac{{x - 2022}}{{1948}} - \frac{{x - 2022}}{{1950}} = 0\)
\(\left( {x - 2022} \right)\left( {\frac{1}{{2011}} + \frac{1}{{2012}} - \frac{1}{{1948}} - \frac{1}{{1950}}} \right) = 0\)
\(x - 2022 = 0\) (vì \(\frac{1}{{2011}} + \frac{1}{{2012}} - \frac{1}{{1948}} - \frac{1}{{1950}} < 0\))
\(x = 2022\)
Vì 2022 chia hết cho 2, không chia hết cho 4, không chia hết cho 5 nên nghiệm của phương trình là một số chia hết cho 2
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
Đáp án : A
+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng khái niệm phương trình bậc nhất một ẩn: Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho và \(a \ne 0\) được gọi là phương trình bậc nhất một ẩn x.
\(3mx + m - 4x = 3{m^2} + 1\)
\(\left( {3m - 4} \right)x + m - 3{m^2} - 1 = 0\)
Để phương trình \(\left( {3m - 4} \right)x + m - 3{m^2} - 1 = 0\) có nghiệm duy nhất thì \(3m - 4 \ne 0\)
\(3m \ne 4\)
\(m \ne \frac{4}{3}\)
Vậy \(m \ne \frac{4}{3}\)
Hình tam giác và hình chữ nhật ở hình dưới có cùng chu vi. Khi đó, giá trị của x là:

Đáp án : C
+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng chu vi hình tam giác: Chu vi hình tam giác bằng tổng độ dài ba cạnh của tam giác
+ Sử dụng chu vi hình chữ nhật: Chu vi hình tam giác bằng hai lần tổng chiều dài và chiều rộng
Chu vi hình tam giác là: \(x + 2 + x + 4 + x + 5 = 3x + 11\)
Chu vi hình chữ nhật là: \(2\left( {x + 1 + x + 4} \right) = 2\left( {2x + 5} \right) = 4x + 10\)
Vì hai hình có chu vi bằng nhau nên: \(3x + 11 = 4x + 10\)
\(4x - 3x = 11 - 10\)
\(x = 1\)
Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
Đáp án : A
+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng khái niệm nghiệm của phương trình: Số \({x_0}\)được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\)nếu giá trị của A(x) và B(x) tại \({x_0}\)bằng nhau.
\(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\)
\(\frac{{21x}}{{24}} - \frac{{120\left( {x - 9} \right)}}{{24}} = \frac{{4\left( {20x + 1,5} \right)}}{{24}}\)
\(21x - 120x + 1080 = 80x + 6\)
\( - 179x = - 1074\)
\(x = 6\)
Vì phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) nên phương trình (2) có nghiệm là \(x = 2\)
\(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Với \(x = 2\) thay vào phương trình (2) ta có:
\(2\left( {a - 1} \right)2 - a\left( {2 - 1} \right) = 2a + 3\)
\(4a - 4 - a = 2a + 3\)
\(a = 7\)
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
Đáp án : D
\(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\)
\(\frac{{4\left( {x + 1} \right)}}{{12}} + \frac{{9\left( {2x + 1} \right)}}{{12}} = \frac{{2\left( {5x + 3} \right)}}{{12}} + \frac{{7 + 12x}}{{12}}\)
\(4x + 4 + 18x + 9 = 10x + 6 + 7 + 12x\)
\(22x + 13 = 22x + 13\)
\(0 = 0\) (luôn đúng)
Vậy phương trình đã cho có vô số nghiệm
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:

Đáp án : B
Hình bên có gồm hai hình chữ nhật:
+ Hình chữ nhật độ dài 2 kích thước là 12m và x (mét) nên diện tích hình là: \(12x\left( {{m^2}} \right)\)
+ Hình chữ nhật có độ dài 2 kích thước là 6m và 4m nên diện tích hình là: \(4.6 = 24\left( {{m^2}} \right)\)
Mà diện tích của cả hình đó bằng \(168{m^2}\) nên ta có:
\(12x + 24 = 168\)
\(12x = 144\)
\(x = 12\)
Vậy \(x = 12m\)
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
Đáp án : D

Giả sử ô tô gặp xe máy tại C như trên hình.
Gọi x (giờ) (x > 0) là khoảng thời gian chuyển động của ôtô đi từ A đến C.
Ô tô đi với vận tốc 48km/h nên quãng đường AC bằng: 48.x (km) (1)
Vì xe máy đi trước ôtô 1 giờ nên thời gian xe máy đi từ A đến C bằng: x + 1 (h)
Xe máy đi với vận tốc 32km/h nên quãng đường AC bằng: 32(x + 1) (km) (2)
Từ (1) và (2) ta có phương trình: 48x = 32(x + 1).
Vậy phương trình là: 48x = 32(x + 1).
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
Đáp án : B
\(\left( {{m^2} - 3m + 2} \right)x = m - 2\left( * \right)\)
Xét \({m^2} - 3m + 2 = 0\)
\({m^2} - m - 2m + 2 = 0\)
\(\left( {m - 1} \right)\left( {m - 2} \right) = 0\)
Từ đó tính được \(m = 1;m = 2\)
Với \(m = 1\) thay vào (*) ta có: \(0.x = - 1\) (vô lí) nên phương trình (*) vô nghiệm.
Với \(m = 2\) thay vào (*) ta có: \(0x = 0\) (luôn đúng) nên phương trình (*) có vô số nghiệm với mọi số thực x.
Số nghiệm của phương trình \(\sqrt x + 1 = 2\sqrt { - x} \) là:
Đáp án : C
Khi \(x = 0\) ta có: \(1 = 0\) (vô lí) nên \(x = 0\) không là nghiệm của phương trình đã cho
Khi \(x < 0\) thì \(\sqrt x \) không xác định
Khi \(x > 0\) thì \(\sqrt { - x} \) không xác định
Vậy trong mọi trường hợp, không có giá trị nào thỏa mãn phương trình.
Vậy phương trình đã cho vô nghiệm
Hình dưới dây mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1ft=0,3048m). Tốc độ v(ft/s) của nước tại thời điểm t(s) được cho bởi công thức \(v = 48 - 30t.\) Thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:

Đáp án : C
Khi xuất phát từ mặt đài phun nước, giọt nước có \(t = 0.\)
Khi giọt nước đạt độ cao tối đa thì \(v = 0.\) Thay vào công thức ta có:
\(0 = 48 - 30t\)
\(30t = 48\)
\(t = 1,6\)
Vậy thời gian để giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là: \(1,6 - 0 = 1,6\) (s)
Bài 1 trong chương trình Toán 8 Chân trời sáng tạo giới thiệu về phương trình bậc nhất một ẩn. Đây là một khái niệm cơ bản nhưng vô cùng quan trọng, là nền tảng cho các kiến thức toán học nâng cao hơn. Việc nắm vững lý thuyết và kỹ năng giải phương trình bậc nhất một ẩn là điều cần thiết để các em học sinh có thể tự tin giải quyết các bài toán liên quan.
Một phương trình bậc nhất một ẩn là một phương trình có dạng ax + b = 0, trong đó:
Ví dụ: 2x + 5 = 0, -3x - 1 = 0, x - 7 = 0
Để giải một phương trình bậc nhất một ẩn, chúng ta thường thực hiện các bước sau:
Ví dụ: Giải phương trình 3x + 6 = 0
Vậy nghiệm của phương trình là x = -2.
Trong các bài kiểm tra và đề thi, các em thường gặp các dạng bài tập trắc nghiệm sau:
Để giải các bài tập trắc nghiệm nhanh và chính xác, các em có thể áp dụng một số mẹo sau:
Dưới đây là một số bài tập trắc nghiệm minh họa để các em luyện tập:
Câu 1: Phương trình nào sau đây là phương trình bậc nhất một ẩn?
Câu 2: Nghiệm của phương trình 5x - 10 = 0 là:
Để nắm vững kiến thức về phương trình bậc nhất một ẩn, các em nên dành thời gian luyện tập thường xuyên. Hãy giải nhiều bài tập khác nhau, từ cơ bản đến nâng cao, để rèn luyện kỹ năng và làm quen với các dạng đề thi. Giaitoan.edu.vn cung cấp một nguồn tài liệu phong phú và đa dạng để các em có thể luyện tập và củng cố kiến thức một cách hiệu quả.
Phương trình bậc nhất một ẩn là một kiến thức quan trọng trong chương trình Toán lớp 8. Việc nắm vững lý thuyết và kỹ năng giải phương trình bậc nhất một ẩn là điều cần thiết để các em học sinh có thể tự tin giải quyết các bài toán liên quan và đạt kết quả tốt trong học tập. Chúc các em học tập tốt!