Chào mừng bạn đến với bài trắc nghiệm Toán 8 Bài 4: Hai hình đồng dạng, thuộc chương trình Chân trời sáng tạo. Bài trắc nghiệm này được thiết kế để giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán về hai hình đồng dạng.
Giaitoan.edu.vn cung cấp bộ câu hỏi trắc nghiệm đa dạng, bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp bạn tự đánh giá năng lực và chuẩn bị tốt nhất cho các bài kiểm tra.
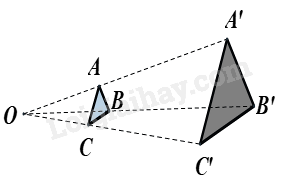
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3.\) Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:
Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) với tâm phối cảnh là:
Chọn đáp án đúng nhất
Cho hình chữ nhật ba hình chữ nhật ABCD, A’B’C’D’, A”B”C”D” sao cho:
+ Hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh
+ Hình A”B”C”D” bằng hình A’B’C’D’
Chọn đáp án đúng
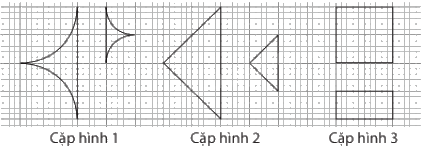
Trong những cặp hình cho ở hình vẽ dưới đây, có mấy cặp hình là hình đồng dạng?
Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA và OB.
Chọn đáp án đúng.
Cho các hình vẽ sau:
Hình nào đồng dạng với hình a?
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3.\) Nếu độ dài cạnh của hình vuông ABCD là 9cm thì độ dài cạnh của hình vuông A’B’C’D’ là:
Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.
Cho các khẳng định sau:
+ Hình thang ABCD và EFGH bằng nhau
+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau
+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’
Có bao nhiêu khẳng định đúng?
Cho tam giác ABC có AB = 4, BC = 7, CA = 6. Cho O, I là điểm phân biệt.
+ Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\)
+ Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\).
Chọn đáp án đúng
Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Qua M vẽ đường thẳng vuông góc với AB cắt AB tại H.
Chọn đáp án đúng
Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh là 10cm và 8cm.
Chọn câu trả lời đúng nhất
Tam giác ABC có chu vi bằng 18cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\). Chu vi tam giác A’B’C’ bằng:
Hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD theo tỉ số đồng dạng k. Biết rằng diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\), diện tích hình vuông ABCD là \(36c{m^2}.\) Khi đó, tỉ số đồng dạng k bằng:
Cho hình tròn H có diện tích bằng \(113,04c{m^2}\). Hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\). Khi đó, diện tích của hình tròn H’ bằng:
Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\). Biết rằng diện tích tam giác ABC bằng \(48c{m^2}.\) Diện tích tam giác AMN bằng:
Cho tam giác ABC. Trên cạnh BC lấy điểm K sao cho \(CK = \frac{2}{3}BC.\) Tìm trên AB điểm H sao cho cạnh HK là hình đồng dạng phối cảnh của cạnh AC (với tâm đồng dạng phối cảnh là điểm B)
: Cho hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 6cm,BC = 8cm,A'B' = 12cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ là:
Cho tam giác ABC có \(AB = 3cm,BC = 4cm,AC = 5cm.\) Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích tam giác A”B”C” bằng \(96c{m^2}\).
Chọn đáp án đúng
Cho hình chữ nhật ABCD có \(AB = \frac{3}{4}BC.\) Hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD theo tỉ số đồng dạng 2. Biết rằng \(A'C' = 10cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ bằng:
Cho hai tấm thảm hình tam giác ABC và A’B’C’, tấm thảm ABC có chu vi bằng 400cm và đồng dạng phối cảnh với tấm thảm A’B’C’ tâm O, tỉ số \(\frac{2}{3}.\) Chu vi tam giác A’B’C’ bằng:
Một tủ sách nghệ thuật ở có dạng như hình vẽ sau:
Trong đó BM, CN, DP, EQ là các ngăn của tủ sách và ngăn EQ có độ dài 4m.
Có bao nhiêu khẳng định đúng trong các khẳng định sau?
+ Ngăn BM là hình đồng dạng phối cảnh với ngăn EQ, với tâm A, tỉ số bằng \(\frac{1}{4}\)
+ Ngăn CN là hình đồng dạng phối cảnh với ngăn DP, với tâm A, tỉ số bằng \(\frac{1}{3}\)
+ \(BM = 1m,CN = 2m,DP = 3m\)
: Cho hai bức tranh hình chữ nhật như hình vẽ sau đây:
Cho bức tranh A’B’C’D’ là hình đồng dạng của bức tranh ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 12cm,BC = 16cm,A'B' = 24cm.\) Khi đó, diện tích bức tranh A’B’C’D’ là:
Một chiếc khăn mặt có dạng hình tam giác ABC có \(AB = 12cm,BC = 16cm,AC = 20cm.\) Một chiếc khăn mặt khác hình tam giác A’B’C’ là hình đồng dạng phối cảnh của chiếc khăn ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Khăn tam giác A”B”C” là hình đồng dạng của khăn A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích chiếc khăn A”B”C” bằng \(1536c{m^2}\).
Chọn đáp án đúng
Một mặt bàn hình chữ nhật ABCD có \(AB = \frac{5}{{12}}BC.\) Mặt bàn hình chữ nhật A’B’C’D’ là hình đồng dạng của mặt bàn hình chữ nhật ABCD có tỉ số đồng dạng 2. Biết rằng \(A'C' = 130cm.\) Khi đó, diện tích mặt bàn hình chữ nhật A’B’C’D’ bằng:
Trong các hình dưới đây, hình nào không thể hiện hình đồng dạng?

Cho hình cánh hoa:

Hình nào dưới đây đồng dạng với hình cánh hoa ở trên?



Trong các loài thực vật sau, loài thực vật nào thể hiện hình đồng dạng?



Biển báo M là hình đồng dạng của biển báo P khi thu nhỏ với tỉ số k bằng:
Cho các hình vẽ dưới đây:
Có bao nhiêu cặp hình đồng dạng trong các hình ở trên?
Không cặp hình nào
Cho hình vẽ:
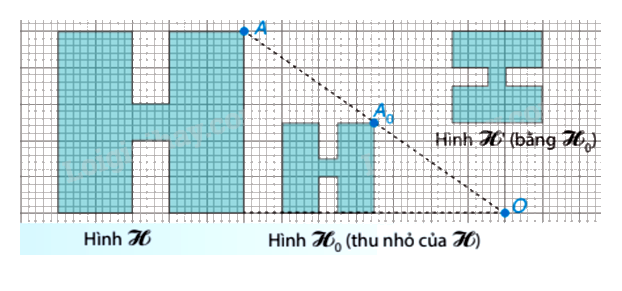
Cho các khẳng định sau:
+ Hình H là hình đồng dạng phối cảnh của hình H 0
+ Hình H ’ là hình đồng dạng phối cảnh của hình H 0
+ Hình H đồng dạng của hình H 0
Có bao nhiêu khẳng định đúng?
Trong các hình con bướm dưới đây, có mấy hình là đồng dạng với nhau
Cho hai bức tranh như hình vẽ dưới đây:

Biết rằng bức tranh trong hình b là bức tranh trong hình a sau khi thu nhỏ với \(k = \frac{2}{3}.\) Nếu kích thước của bức tranh hình a là \(4 \times 6\) thì kích thước của bức tranh trong hình b là:
Hình bên dưới mô tả hai bức tranh kim tử tháp hình vuông những có kích thước khác nhau.
Biết rằng A, B, C, D lần lượt là trung điểm của OA’, OB’, OC’, OD’
Chọn đáp án đúng
Ba cái cây có hình vẽ như sau:
Cây 1 đồng dạng với cây 2 theo tỉ số là x.
Để cây 2 đồng dạng với cây 3 theo tỉ số đồng dạng là x thì:
Cho hai tem thư hình vuông như hình vẽ dưới đây:

Biết rằng tem thư 1 có diện tích là \(144c{m^2}\), tem thư 2 có chu vi là 40cm
Chọn đáp án đúng
Hình ảnh bên dưới là bức tranh Đông Hồ (hình chữ nhật) nhưng có kích thước khác nhau.
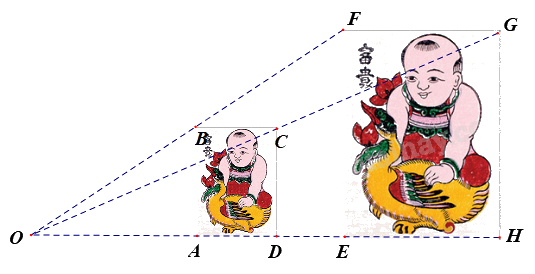
Biết rằng B, C, A, D lần lượt là trung điểm của OF, OG, OE, OH và diện tích của bức tranh ABCD bằng \(100c{m^2}\). Diện tích của bức tranh EFGH là:
Hai cái đĩa có mặt đĩa là hình tròn như hình sau:

Biết rằng mặt đĩa H có diện tích bằng \(113,04c{m^2}\). Mặt đĩa H’ là hình đồng dạng với mặt đĩa H có tỉ số đồng dạng bằng \(2\). Khi đó, diện tích của mặt đĩa H’ bằng:
Lời giải và đáp án
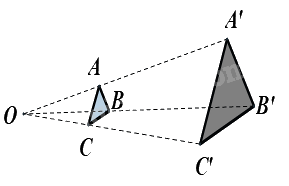
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3.\) Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3\) nên tam giác A’B’C’ và tam giác ABC là đồng dạng phối cảnh với tỉ số vị tự là 3.
Do đó tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là \(\frac{1}{3}\).
Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) với tâm phối cảnh là:
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Chọn đáp án đúng nhất
Đáp án : C
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
+ Hai hình H, H’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Do đó, cả A và B đều đúng
Cho hình chữ nhật ba hình chữ nhật ABCD, A’B’C’D’, A”B”C”D” sao cho:
+ Hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh
+ Hình A”B”C”D” bằng hình A’B’C’D’
Chọn đáp án đúng
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng
Vì hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh và hình A”B”C”D” bằng hình A’B’C’D’ nên
+ Hình A’B’C’D’ đồng dạng với hình ABCD
+ Hình A”B”C”D” đồng dạng với hình ABCD
Do đó, cả A, B đều đúng
Trong những cặp hình cho ở hình vẽ dưới đây, có mấy cặp hình là hình đồng dạng?
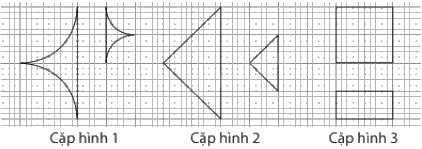
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Các cặp hình đồng dạng là: Cặp hình 1 và cặp hình 2.
Vậy có 2 cặp hình đồng dạng.
Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA và OB.
Chọn đáp án đúng.
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.
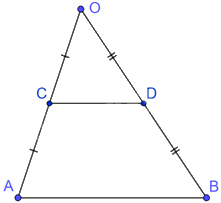
Vì C là trung điểm của OA nên \(OC = \frac{1}{2}OA\)
Vì D là trung điểm của OB nên \(OD = \frac{1}{2}OB\)
Mà O là giao điểm của AC và BD nên cạnh CD là hình đồng dạng phối cảnh của cạnh AB với tỉ số đồng dạng \(k = \frac{1}{2}\), tâm phối cảnh là điểm O.
Do đó, cạnh CD là hình đồng dạng của cạnh AB với tỉ số \(k = \frac{1}{2}\)
Suy ra, cả A, B đều đúng.
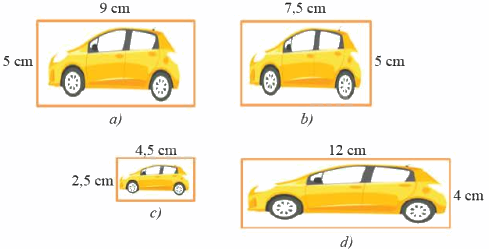
Cho các hình vẽ sau:
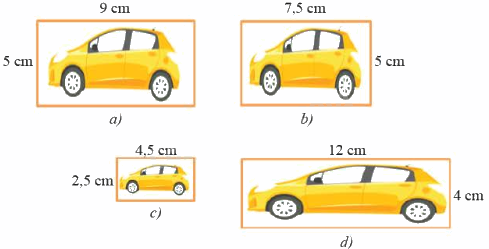
Hình nào đồng dạng với hình a?
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì \(\frac{5}{5} \ne \frac{9}{{7,5}}\) nên hình a và hình b không phải là hai hình đồng dạng
Vì \(\frac{5}{{2,5}} = \frac{9}{{4,5}}\) nên hình a và hình c là hai hình đồng dạng với nhau
Vì \(\frac{{12}}{9} \ne \frac{4}{5}\) nên hình a và hình d không phải là hai hình đồng dạng
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng là: \(\frac{6}{3} = 2\)
Hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3.\) Nếu độ dài cạnh của hình vuông ABCD là 9cm thì độ dài cạnh của hình vuông A’B’C’D’ là:
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.
Vì hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3\) nên cạnh của hình vuông A’B’C’D’ gấp 3 lần cạnh của hình vuông ABCD. Do đó, cạnh của hình vuông A’B’C’D’ là: \(9.3 = 27\left( {cm} \right)\)
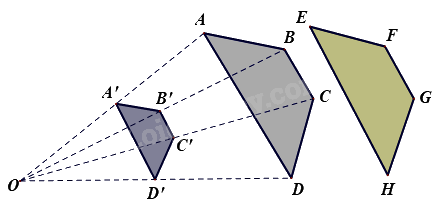
Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.
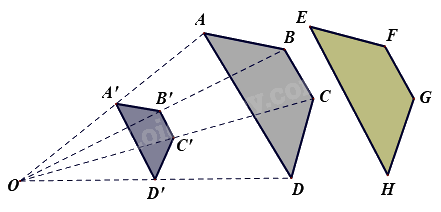
Cho các khẳng định sau:
+ Hình thang ABCD và EFGH bằng nhau
+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau
+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’
Có bao nhiêu khẳng định đúng?
Đáp án : D
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Hình thang ABCD và EFGH bằng nhau.
Vì các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD nên \(OA = 2OA',OB = 2OB',OC = 2OC',OD = 2OD'\).
Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’.
Do đó, hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau.
Vậy cả 3 khẳng định trên đều đúng
Cho tam giác ABC có AB = 4, BC = 7, CA = 6. Cho O, I là điểm phân biệt.
+ Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\)
+ Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\).
Chọn đáp án đúng
Đáp án : A
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh nên \(\frac{OA'}{OA}=\frac{OB'}{OB}=\frac{OC'}{OC}\) suy ra \( \Delta A'B'C'\backsim \Delta ABC\), do đó \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=3\)
suy ra \(A'B'=12;B'C'=21;C'A'=18\)
Vì tam giác A”B”C” là hình đồng dạng phối cảnh của tam giác ABC với I là tâm đồng dạng phối cảnh nên \(\frac{IA''}{IA}=\frac{IB''}{IB}=\frac{IC''}{IC}\) suy ra \( \Delta A''B''C''\backsim \Delta ABC\), do đó \(\frac{A''B''}{AB}=\frac{B''C''}{BC}=\frac{C''A''}{CA}=3\)
suy ra \(A''B''=12;B''C''=21;C''A''=18\)
Do đó, \(A'B'=A''B''=21,B'C'=B''C''=21,C'A'=C''A''=18\)
suy ra \(\frac{A''B''}{A'B'}=\frac{C''B''}{C'B'}=\frac{A''C''}{A'C'}=1\)
Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Qua M vẽ đường thẳng vuông góc với AB cắt AB tại H.
Chọn đáp án đúng
Đáp án : A
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H ’bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
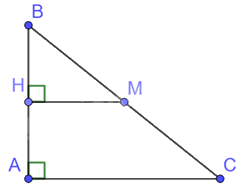
Ta có: \(HM \bot AB,AC \bot AB\) nên HM//AC
Tam giác ABC có: M là trung điểm của BC, HM//AC nên H là trung điểm của AB.
Do đó, \(\frac{{BH}}{{BA}} = \frac{1}{2}\)
Lại có: Mà là trung điểm của BC nên \(\frac{{BM}}{{BC}} = \frac{1}{2}\)
Suy ra: \(\frac{{BH}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{2}\)
Mà đường thẳng AH và MC cùng đi qua điểm B.
Do đó, HM là hình đồng dạng phối cảnh của cạnh AC, tâm B, tỉ số \(\frac{1}{2}\)
Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh là 10cm và 8cm.
Chọn câu trả lời đúng nhất
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
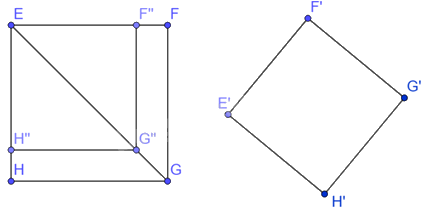
Trên các đoạn thẳng EF, EG, EH, ta lần lượt lấy các điểm F”, G”, H” sao cho \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}.\) Theo định lý Thalès đảo ta có: F”G”//FG, G”H”//GH.
Mà \(\widehat{F''EH''}={{90}^{0}}\) nên tứ giác EF”G”H” là hình chữ nhật.
Mặt khác, ta có: \(\frac{EF''}{EF}=\frac{F''G''}{FG}=\frac{G''H''}{GH}=\frac{H''E}{HE}=\frac{4}{5}\) (hệ quả định lí Thalès)
Suy ra \(EF''=F''G''=G''H''=H''E=8cm\) .
Do đó, tứ giác EF”G”H” là hình vuông có độ dài cạnh bằng 8cm.
Suy ra, hai hình vuông EF”G”H” và E’F’G’H’ bằng nhau
Vì \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}\) nên hình vuông EF”G”H” đồng dạng phối cảnh với hình vuông EFGH hay hình vuông E’F’G’H’ đồng dạng phối cảnh với hình vuông EFGH.
Vậy hình vuông E’F’G’H’ đồng dạng với hình vuông EFGH.
Tam giác ABC có chu vi bằng 18cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\). Chu vi tam giác A’B’C’ bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Tam giác ABC có chu vi bằng 18cm nên \(AB + BC + CA = 18\)
Chu vi tam giác A’B’C’ là: \(P' = A'B' + A'C' + B'C'\)
Vì tam A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\) nên \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{3}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{{A'B' + A'C' + B'C'}}{{AB + AC + BC}} = \frac{{P'}}{{18}} = \frac{1}{3}\)
\( \Rightarrow P' = 18:3 = 6\left( {cm} \right)\)
Vậy chu vi tam giác A’B’C’ bằng 6cm
Hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD theo tỉ số đồng dạng k. Biết rằng diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\), diện tích hình vuông ABCD là \(36c{m^2}.\) Khi đó, tỉ số đồng dạng k bằng:
Đáp án : A
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H ’bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\) nên ta có: \(A'B{'^2} = 64 \Rightarrow A'B' = 8cm\)
Vì diện tích hình vuông ABCD là \(36c{m^2}\) nên ta có: \(A{B^2} = 36 \Rightarrow AB = 6cm\)
Vì hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD tỉ số đồng dạng k nên:
\(k = \frac{{A'B'}}{{AB}} = \frac{8}{6} = \frac{4}{3}\)
Vậy tỉ số đồng dạng là \(\frac{4}{3}\)
Cho hình tròn H có diện tích bằng \(113,04c{m^2}\). Hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\). Khi đó, diện tích của hình tròn H’ bằng:
Đáp án : C
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình tròn H có diện tích bằng \(113,04c{m^2}\) nên bán kính của hình tròn là: \({R^2} = \frac{{113,04}}{{3,14}} = 36 \Rightarrow R = 6cm\)
Vì hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\) nên bán kính hình tròn H’ là: \(R' = \frac{R}{2} = 3\left( {cm} \right)\)
Diện tích hình tròn H’ là: \({3^2}.3,14 = 28,26c{m^2}\)
Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\). Biết rằng diện tích tam giác ABC bằng \(48c{m^2}.\) Diện tích tam giác AMN bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
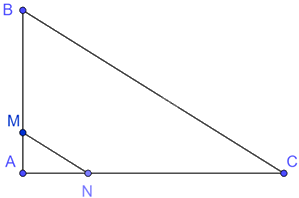
Vì đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{4} \Rightarrow AB = 4AM,AC = 4AN\)
Diện tích tam giác AMN vuông tại A là: \({S_{AMN}} = \frac{1}{2}AM.AN\)
Vì tam giác ABC vuông tại A nên diện tích tam giác ABC là:
\(\frac{1}{2}AB.AC = 48 \Rightarrow \frac{1}{2}.4AM.4AN = 48 \Rightarrow \frac{1}{2}AM.AN = 3\left( {c{m^2}} \right)\)
Do đó, diện tích tam giác AMN bằng \(3c{m^2}\).
Cho tam giác ABC. Trên cạnh BC lấy điểm K sao cho \(CK = \frac{2}{3}BC.\) Tìm trên AB điểm H sao cho cạnh HK là hình đồng dạng phối cảnh của cạnh AC (với tâm đồng dạng phối cảnh là điểm B)
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
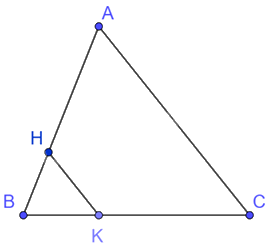
Vì H thuộc AB và HK là hình đồng dạng phối cảnh của cạnh AC, với tâm đồng dạng phối cảnh là điểm B nên \(\frac{{HK}}{{AC}} = \frac{{BK}}{{BC}} = \frac{{BH}}{{BA}}\)
Mà \(CK = \frac{2}{3}BC \Rightarrow \frac{{BK}}{{BC}} = \frac{1}{3} \Rightarrow \frac{{BH}}{{BA}} = \frac{{KH}}{{AC}} = \frac{1}{3}\)
Do đó, điểm H cần tìm thuộc đoạn thẳng AB sao cho \(BH = \frac{1}{3}AB\).
: Cho hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 6cm,BC = 8cm,A'B' = 12cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ là:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k nên \(k = \frac{{A'B'}}{{AB}} = \frac{{12}}{6} = 2\)
Ta có: \(\frac{{B'C'}}{{BC}} = 2 \Rightarrow B'C' = 8.2 = 16\left( {cm} \right)\)
Diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 12.16 = 192\left( {c{m^2}} \right)\)
Cho tam giác ABC có \(AB = 3cm,BC = 4cm,AC = 5cm.\) Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích tam giác A”B”C” bằng \(96c{m^2}\).
Chọn đáp án đúng
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2 nên \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=2\)
\(\Rightarrow A'B'=6cm,B'C'=8cm,A'C'=10cm\)
Vì \(A'C{{'}^{2}}=A'B{{'}^{2}}+B'C{{'}^{2}}\left( {{10}^{2}}={{8}^{2}}+{{6}^{2}} \right)\) nên tam giác A’B’C’ vuông tại B’
Vì tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x nên \(\Delta A''B''C''\backsim \Delta A'B'C'\)
Do đó, \(\widehat{A''B''C''}=\widehat{A'B'C'}=90\) và \(\frac{A''B''}{A'B'}=\frac{A''C''}{A'C'}=\frac{B''C''}{B'C'}=x\Rightarrow A''B''=6x,A''C''=10x,B''C''=8x\)
Vì tam giác A”B”C” vuông tại B” nên diện tích tam giác A”B”C” là:
\({{S}_{A''B''C''}}=\frac{1}{2}B''A''.B''C''\Rightarrow \frac{1}{2}.6x.8x=96\Rightarrow {{x}^{2}}=4\Rightarrow x=2\) (do \(x>0\))
Cho hình chữ nhật ABCD có \(AB = \frac{3}{4}BC.\) Hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD theo tỉ số đồng dạng 2. Biết rằng \(A'C' = 10cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ bằng:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD có tỉ số đồng dạng 2 nên \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = 2\)
Mà \(AB = \frac{3}{4}BC \Rightarrow A'B' = \frac{3}{4}B'C'.\)
Vì A’B’C’D’ là hình chữ nhật nên \(\widehat {A'B'C'} = {90^0}\)
Do đó, tam giác A’B’C’ vuông tại B’. Áp dụng định lý Pytago vào tam giác A’B’C’ vuông tại B’ ta có: \(A'C{'^2} = A'B{'^2} + B'C{'^2}\) (1)
Thay \(A'B' = \frac{3}{4}B'C'\) vào (1) ta có:
\({\left( {\frac{3}{4}B'C'} \right)^2} + B'C{'^2} = {10^2}\)
\(\frac{{25}}{{16}}B'C{'^2} = 100\)
\(B'C{'^2} = 64\) nên \(B'C' = 8cm\)
Do đó, \(A'B' = 8.\frac{3}{4} = 6\left( {cm} \right)\)
Vậy diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 6.8 = 48\left( {c{m^2}} \right)\)
Cho hai tấm thảm hình tam giác ABC và A’B’C’, tấm thảm ABC có chu vi bằng 400cm và đồng dạng phối cảnh với tấm thảm A’B’C’ tâm O, tỉ số \(\frac{2}{3}.\) Chu vi tam giác A’B’C’ bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Chu vi tấm thảm ABC là: \(AB + BC + AC = 400\)
Chu vi tấm thảm A’B’C’ là: \(P' = A'B' + B'C' + A'C'\)
Vì tấm thảm ABC đồng dạng phối cảnh với tấm thảm A’B’C’ tâm O, tỉ số \(\frac{2}{3}\) nên ta có:
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{2}{3}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{{AB + BC + AC}}{{A'B' + B'C' + A'C'}} = \frac{{400}}{{P'}} = \frac{2}{3}\) nên \(P' = 400.\frac{3}{2} = 600\left( {cm} \right)\)
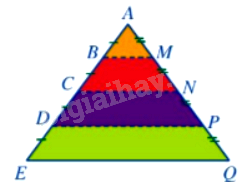
Một tủ sách nghệ thuật ở có dạng như hình vẽ sau:
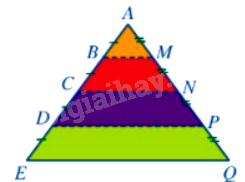
Trong đó BM, CN, DP, EQ là các ngăn của tủ sách và ngăn EQ có độ dài 4m.
Có bao nhiêu khẳng định đúng trong các khẳng định sau?
+ Ngăn BM là hình đồng dạng phối cảnh với ngăn EQ, với tâm A, tỉ số bằng \(\frac{1}{4}\)
+ Ngăn CN là hình đồng dạng phối cảnh với ngăn DP, với tâm A, tỉ số bằng \(\frac{1}{3}\)
+ \(BM = 1m,CN = 2m,DP = 3m\)
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì \(\frac{{AM}}{{AQ}} = \frac{{AB}}{{AE}}\left( { = \frac{1}{4}} \right)\) và các đường thẳng BE và MQ cắt nhau tại A nên BM là hình đồng dạng phối cảnh với EQ, tâm A, tỉ số đồng dạng \(\frac{1}{4}\)
Vì \(\frac{{AC}}{{AD}} = \frac{{AN}}{{AP}}\left( { = \frac{2}{3}} \right)\) và các đường thẳng DC và NP cắt nhau tại A nên CN là hình đồng dạng phối cảnh với DP, tâm A, tỉ số đồng dạng \(\frac{2}{3}\)
Trong tam giác AQE có: \(\frac{{AM}}{{AQ}} = \frac{{AB}}{{AE}}\left( { = \frac{1}{4}} \right)\) nên BM//EQ.
Áp dụng hệ quả định lý Thalès vào tam giác AQE có:
\(\frac{{BM}}{{EQ}} = \frac{{AB}}{{AE}} \Rightarrow \frac{{BM}}{4} = \frac{1}{4} \Rightarrow BM = 1\left( m \right)\)
Trong tam giác AQE có: \(\frac{{AD}}{{AE}} = \frac{{AP}}{{AQ}}\left( { = \frac{3}{4}} \right)\) nên DP//EQ.
Theo hệ quả định lý Thalès vào tam giác AQE có:
\(\frac{{PD}}{{EQ}} = \frac{{AP}}{{AQ}} \Rightarrow \frac{{DP}}{4} = \frac{3}{4} \Rightarrow DP = 3\left( m \right)\)
Trong tam giác ADP có: \(\frac{{AC}}{{AD}} = \frac{{AN}}{{AP}}\left( { = \frac{2}{3}} \right)\) nên CN//DP.
Theo hệ quả định lý Thalès vào tam giác APD có:
\(\frac{{CN}}{{DP}} = \frac{{AC}}{{AD}} \Rightarrow \frac{{CN}}{3} = \frac{2}{3} \Rightarrow CN = 2\left( m \right)\)
Vậy có 2 khẳng định đúng
: Cho hai bức tranh hình chữ nhật như hình vẽ sau đây:
Cho bức tranh A’B’C’D’ là hình đồng dạng của bức tranh ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 12cm,BC = 16cm,A'B' = 24cm.\) Khi đó, diện tích bức tranh A’B’C’D’ là:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k nên \(k = \frac{{A'B'}}{{AB}} = \frac{{24}}{{12}} = 2\)
Ta có: \(\frac{{B'C'}}{{BC}} = 2 \Rightarrow B'C' = 16.2 = 32\left( {cm} \right)\)
Diện tích bức tranh A’B’C’D’ là: \(A'B'.B'C' = 24.32 = 768\left( {c{m^2}} \right)\)
Một chiếc khăn mặt có dạng hình tam giác ABC có \(AB = 12cm,BC = 16cm,AC = 20cm.\) Một chiếc khăn mặt khác hình tam giác A’B’C’ là hình đồng dạng phối cảnh của chiếc khăn ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Khăn tam giác A”B”C” là hình đồng dạng của khăn A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích chiếc khăn A”B”C” bằng \(1536c{m^2}\).
Chọn đáp án đúng
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2 nên \(\Delta A'B'C'\backsim \Delta ABC\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=2\)
\(\Rightarrow A'B'=24cm,B'C'=32cm,A'C'=40cm\)
Vì \(A'C{{'}^{2}}=A'B{{'}^{2}}+B'C{{'}^{2}}\left( {{40}^{2}}={{32}^{2}}+{{24}^{2}} \right)\) nên tam giác A’B’C’ vuông tại B’
Vì tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x nên \(\Delta A''B''C''\backsim \Delta A'B'C'\)
Do đó, \(\widehat{A''B''C''}=\widehat{A'B'C'}=90\) và \(\frac{A''B''}{A'B'}=\frac{A''C''}{A'C'}=\frac{B''C''}{B'C'}=x\Rightarrow A''B''=24x,A''C''=40x,B''C''=32x\)
Vì tam giác A”B”C” vuông tại B” nên diện tích tam giác A”B”C” là:
\({{S}_{A''B''C''}}=\frac{1}{2}B''A''.B''C''\Rightarrow \frac{1}{2}.24x.32x=1536\Rightarrow {{x}^{2}}=4\Rightarrow x=2\)(do \(x>0\))
Một mặt bàn hình chữ nhật ABCD có \(AB = \frac{5}{{12}}BC.\) Mặt bàn hình chữ nhật A’B’C’D’ là hình đồng dạng của mặt bàn hình chữ nhật ABCD có tỉ số đồng dạng 2. Biết rằng \(A'C' = 130cm.\) Khi đó, diện tích mặt bàn hình chữ nhật A’B’C’D’ bằng:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD có tỉ số đồng dạng 2 nên \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = 2\)
Mà \(AB = \frac{5}{{12}}BC \Rightarrow A'B' = \frac{5}{{12}}B'C'.\)
Vì A’B’C’D’ là hình chữ nhật nên \(\widehat {A'B'C'} = {90^0}\)
Do đó, tam giác A’B’C’ vuông tại B’. Áp dụng định lý Pytago vào tam giác A’B’C’ vuông tại B’ ta có: \(A'C{'^2} = A'B{'^2} + B'C{'^2}\) (1)
Thay \(A'B' = \frac{5}{{12}}B'C'\) vào (1) ta có:
\({\left( {\frac{5}{{12}}B'C'} \right)^2} + B'C{'^2} = {130^2}\)
\(\frac{{169}}{{144}}B'C{'^2} = 16900\)
\(B'C{'^2} = 14400\) nên \(B'C' = 120cm\)
Do đó, \(A'B' = \frac{5}{{12}}.120 = 50\left( {cm} \right)\)
Vậy diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 50.120 = 6000\left( {c{m^2}} \right)\)
Trong các hình dưới đây, hình nào không thể hiện hình đồng dạng?

Đáp án : D
Các hình a, b, c đều thể hiện hình đồng dạng, chỉ có hình d là không thể hiện hình đồng dạng.
Cho hình cánh hoa:

Hình nào dưới đây đồng dạng với hình cánh hoa ở trên?



Đáp án : B
Trong các loài thực vật sau, loài thực vật nào thể hiện hình đồng dạng?



Đáp án : D
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
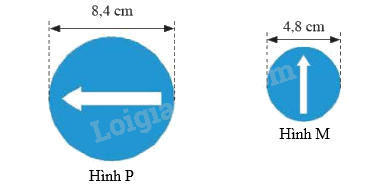
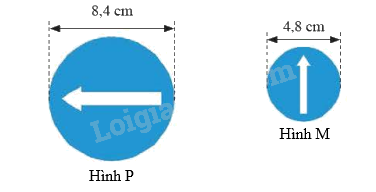
Biển báo M là hình đồng dạng của biển báo P khi thu nhỏ với tỉ số k bằng:
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Ta có: \(k = \frac{{4,8}}{{8,4}} = \frac{4}{7}\) nên biển báo M là hình đồng dạng của biển báo P khi thu nhỏ với tỉ số \(k = \frac{4}{7}\)
Cho các hình vẽ dưới đây:
Có bao nhiêu cặp hình đồng dạng trong các hình ở trên?
Không cặp hình nào
Đáp án : C
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Các cặp hình đồng dạng là: Hình a và hình c, hình b và hình d.
Vậy có 2 cặp hình đồng dạng.
Cho hình vẽ:
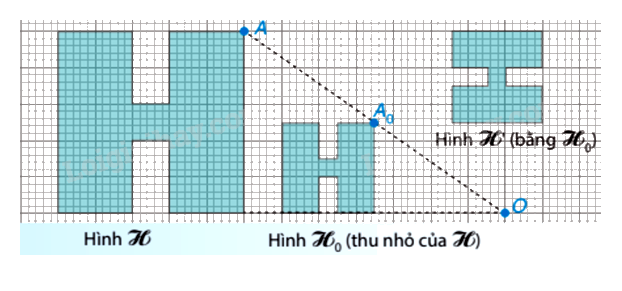
Cho các khẳng định sau:
+ Hình H là hình đồng dạng phối cảnh của hình H 0
+ Hình H ’ là hình đồng dạng phối cảnh của hình H 0
+ Hình H đồng dạng của hình H 0
Có bao nhiêu khẳng định đúng?
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng
Hình H là hình đồng dạng phối cảnh của hình H 0
Mà hình H ’ bằng với hình H 0 nên hình H đồng dạng của hình H 0
Vì hình H là hình đồng dạng phối cảnh của hình H 0 nên H là hình đồng dạng của hình H 0
Vậy cả ba khẳng định trên đều đúng
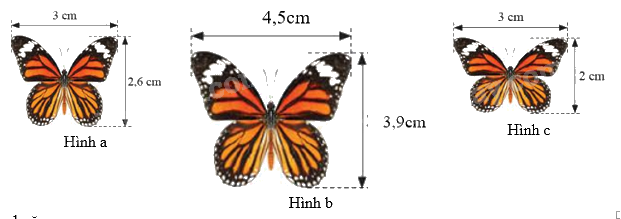
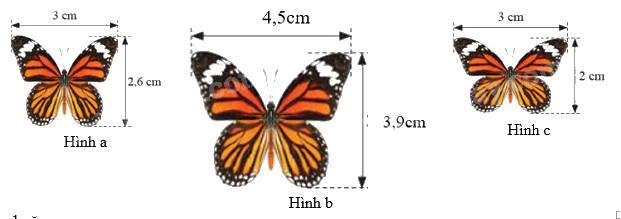
Trong các hình con bướm dưới đây, có mấy hình là đồng dạng với nhau
Đáp án : A
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì \(\frac{{4,5}}{3} = \frac{{3,9}}{{2,6}}\left( { = \frac{3}{2}} \right)\) nên hình b đồng dạng với hình a với tỉ số \(\frac{3}{2}\)
Vì \(\frac{{4,5}}{3} \ne \frac{{3,9}}{2}\) nên hai hình b và c không đồng dạng với nhau
Vì \(\frac{3}{3} \ne \frac{2}{{2,6}}\) nên hai hình a và c không đồng dạng với nhau
Cho hai bức tranh như hình vẽ dưới đây:

Biết rằng bức tranh trong hình b là bức tranh trong hình a sau khi thu nhỏ với \(k = \frac{2}{3}.\) Nếu kích thước của bức tranh hình a là \(4 \times 6\) thì kích thước của bức tranh trong hình b là:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì rằng bức tranh trong hình b là bức tranh trong hình a sau khi thu nhỏ với \(k = \frac{2}{3}\) nên kích thước ở hình b là: \(4.\frac{2}{3} = \frac{8}{3}\) và \(6.\frac{2}{3} = 4\)
Vậy kích thước của bức tranh trong hình b là: \(\frac{8}{3} \times 4\)
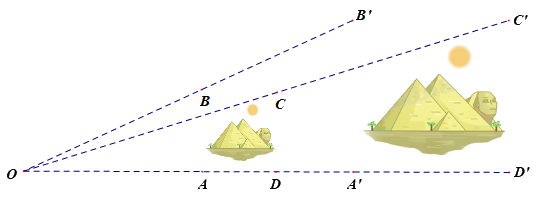
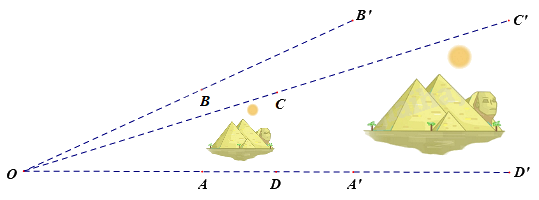
Hình bên dưới mô tả hai bức tranh kim tử tháp hình vuông những có kích thước khác nhau.
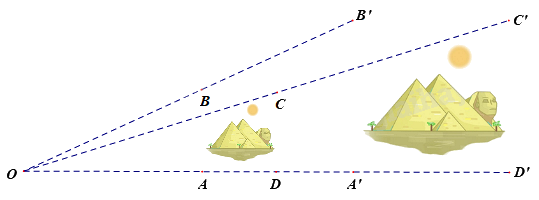
Biết rằng A, B, C, D lần lượt là trung điểm của OA’, OB’, OC’, OD’
Chọn đáp án đúng
Đáp án : A
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì A, B, C, D lần lượt là trung điểm của OA’, OB’, OC’, OD’ nên \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = \frac{{OD'}}{{OD}} = 2\)
Lại có các đường thẳng AA’, BB’, CC’, DD’ cùng đi qua điểm O.
Do đó, bức tranh A’B’C’D’ là hình đồng dạng phối cảnh của bức tranh ABCD, tâm đồng dạng phối cảnh là điểm O, tỉ số 2
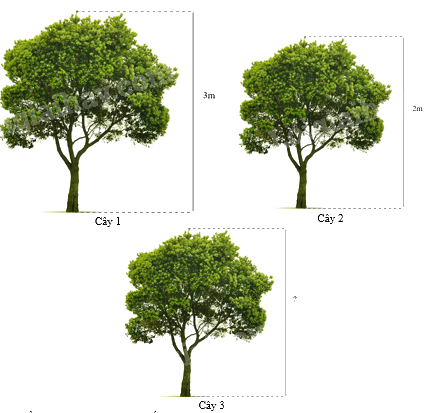
Ba cái cây có hình vẽ như sau:
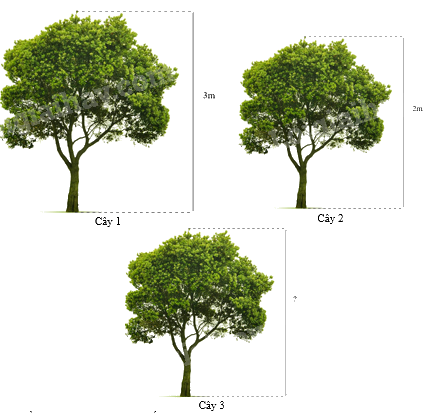
Cây 1 đồng dạng với cây 2 theo tỉ số là x.
Để cây 2 đồng dạng với cây 3 theo tỉ số đồng dạng là x thì:
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Cây 1 đồng dạng với cây 2 theo tỉ số là \(x = \frac{3}{2}\)
Để cây 2 đồng dạng với cây 3 theo tỉ số đồng dạng là \(\frac{3}{2}\) thì \(? = 2:\frac{3}{2} = \frac{4}{3}\left( m \right)\)
Cho hai tem thư hình vuông như hình vẽ dưới đây:

Biết rằng tem thư 1 có diện tích là \(144c{m^2}\), tem thư 2 có chu vi là 40cm
Chọn đáp án đúng
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Độ dài cạnh của tem thư 1 là: \(\sqrt {144} = 12\left( {cm} \right)\)
Độ dài cạnh của tem thư 2 là: \(40:4 = 10\left( {cm} \right)\)
Do đó, tem thư 1 là hình đồng dạng với tem thư 2 với tỉ số: \(\frac{{12}}{{10}} = \frac{6}{5}\)
Hình ảnh bên dưới là bức tranh Đông Hồ (hình chữ nhật) nhưng có kích thước khác nhau.
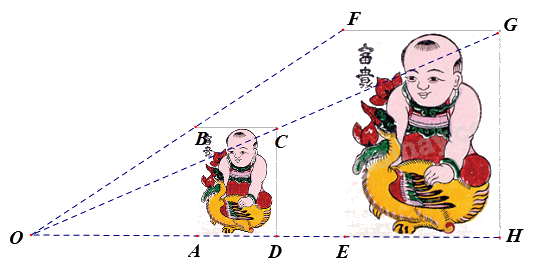
Biết rằng B, C, A, D lần lượt là trung điểm của OF, OG, OE, OH và diện tích của bức tranh ABCD bằng \(100c{m^2}\). Diện tích của bức tranh EFGH là:
Đáp án : A
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì B, C, A, D lần lượt là trung điểm của OF, OG, OE, OH nên \(\frac{{OB}}{{FO}} = \frac{{OA}}{{OE}} = \frac{{OD}}{{OH}} = \frac{{OC}}{{OG}} = \frac{1}{2}\) và các đường thẳng AD, EH, GC, FB cùng đi qua điểm O nên hình ABCD là hình đồng dạng phối cảnh với hình EFGH tâm O tỉ số \(\frac{1}{2}\).
Do đó, \(FG = 2BC,FE = 2AB\)
Diện tích bức tranh ABCD là: \(AB.BC = 100\left( {c{m^2}} \right)\)
Diện tích bức tranh EFGH là: \(FE.FG = 2AB.2BC = 4AB.BC = 4.100 = 400\left( {c{m^2}} \right)\)
Hai cái đĩa có mặt đĩa là hình tròn như hình sau:

Biết rằng mặt đĩa H có diện tích bằng \(113,04c{m^2}\). Mặt đĩa H’ là hình đồng dạng với mặt đĩa H có tỉ số đồng dạng bằng \(2\). Khi đó, diện tích của mặt đĩa H’ bằng:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì mặt đĩa H có diện tích bằng \(113,04c{m^2}\) nên bán kính của mặt đĩa H là: \({R^2} = \frac{{113,04}}{{3,14}} = 36 \Rightarrow R = 6cm\)
Vì mặt đĩa H’ là hình đồng dạng với mặt đĩa H có tỉ số đồng dạng bằng 2 nên bán kính mặt đĩa H’ là: \(R' = 2R = 12\left( {cm} \right)\)
Diện tích mặt đĩa H’ là: \({12^2}.3,14 = 452,16\left( {c{m^2}} \right)\)
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3.\) Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:

Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) với tâm phối cảnh là:
Chọn đáp án đúng nhất
Cho hình chữ nhật ba hình chữ nhật ABCD, A’B’C’D’, A”B”C”D” sao cho:
+ Hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh
+ Hình A”B”C”D” bằng hình A’B’C’D’
Chọn đáp án đúng
Trong những cặp hình cho ở hình vẽ dưới đây, có mấy cặp hình là hình đồng dạng?

Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA và OB.
Chọn đáp án đúng.
Cho các hình vẽ sau:

Hình nào đồng dạng với hình a?
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3.\) Nếu độ dài cạnh của hình vuông ABCD là 9cm thì độ dài cạnh của hình vuông A’B’C’D’ là:
Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.

Cho các khẳng định sau:
+ Hình thang ABCD và EFGH bằng nhau
+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau
+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’
Có bao nhiêu khẳng định đúng?
Cho tam giác ABC có AB = 4, BC = 7, CA = 6. Cho O, I là điểm phân biệt.
+ Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\)
+ Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\).
Chọn đáp án đúng
Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Qua M vẽ đường thẳng vuông góc với AB cắt AB tại H.
Chọn đáp án đúng
Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh là 10cm và 8cm.
Chọn câu trả lời đúng nhất
Tam giác ABC có chu vi bằng 18cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\). Chu vi tam giác A’B’C’ bằng:
Hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD theo tỉ số đồng dạng k. Biết rằng diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\), diện tích hình vuông ABCD là \(36c{m^2}.\) Khi đó, tỉ số đồng dạng k bằng:
Cho hình tròn H có diện tích bằng \(113,04c{m^2}\). Hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\). Khi đó, diện tích của hình tròn H’ bằng:
Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\). Biết rằng diện tích tam giác ABC bằng \(48c{m^2}.\) Diện tích tam giác AMN bằng:
Cho tam giác ABC. Trên cạnh BC lấy điểm K sao cho \(CK = \frac{2}{3}BC.\) Tìm trên AB điểm H sao cho cạnh HK là hình đồng dạng phối cảnh của cạnh AC (với tâm đồng dạng phối cảnh là điểm B)
: Cho hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 6cm,BC = 8cm,A'B' = 12cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ là:
Cho tam giác ABC có \(AB = 3cm,BC = 4cm,AC = 5cm.\) Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích tam giác A”B”C” bằng \(96c{m^2}\).
Chọn đáp án đúng
Cho hình chữ nhật ABCD có \(AB = \frac{3}{4}BC.\) Hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD theo tỉ số đồng dạng 2. Biết rằng \(A'C' = 10cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ bằng:
Cho hai tấm thảm hình tam giác ABC và A’B’C’, tấm thảm ABC có chu vi bằng 400cm và đồng dạng phối cảnh với tấm thảm A’B’C’ tâm O, tỉ số \(\frac{2}{3}.\) Chu vi tam giác A’B’C’ bằng:
Một tủ sách nghệ thuật ở có dạng như hình vẽ sau:

Trong đó BM, CN, DP, EQ là các ngăn của tủ sách và ngăn EQ có độ dài 4m.
Có bao nhiêu khẳng định đúng trong các khẳng định sau?
+ Ngăn BM là hình đồng dạng phối cảnh với ngăn EQ, với tâm A, tỉ số bằng \(\frac{1}{4}\)
+ Ngăn CN là hình đồng dạng phối cảnh với ngăn DP, với tâm A, tỉ số bằng \(\frac{1}{3}\)
+ \(BM = 1m,CN = 2m,DP = 3m\)
: Cho hai bức tranh hình chữ nhật như hình vẽ sau đây:

Cho bức tranh A’B’C’D’ là hình đồng dạng của bức tranh ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 12cm,BC = 16cm,A'B' = 24cm.\) Khi đó, diện tích bức tranh A’B’C’D’ là:
Một chiếc khăn mặt có dạng hình tam giác ABC có \(AB = 12cm,BC = 16cm,AC = 20cm.\) Một chiếc khăn mặt khác hình tam giác A’B’C’ là hình đồng dạng phối cảnh của chiếc khăn ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Khăn tam giác A”B”C” là hình đồng dạng của khăn A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích chiếc khăn A”B”C” bằng \(1536c{m^2}\).
Chọn đáp án đúng
Một mặt bàn hình chữ nhật ABCD có \(AB = \frac{5}{{12}}BC.\) Mặt bàn hình chữ nhật A’B’C’D’ là hình đồng dạng của mặt bàn hình chữ nhật ABCD có tỉ số đồng dạng 2. Biết rằng \(A'C' = 130cm.\) Khi đó, diện tích mặt bàn hình chữ nhật A’B’C’D’ bằng:
Trong các hình dưới đây, hình nào không thể hiện hình đồng dạng?

Cho hình cánh hoa:

Hình nào dưới đây đồng dạng với hình cánh hoa ở trên?



Trong các loài thực vật sau, loài thực vật nào thể hiện hình đồng dạng?



Biển báo M là hình đồng dạng của biển báo P khi thu nhỏ với tỉ số k bằng:

Cho các hình vẽ dưới đây:

Có bao nhiêu cặp hình đồng dạng trong các hình ở trên?
Không cặp hình nào
Cho hình vẽ:

Cho các khẳng định sau:
+ Hình H là hình đồng dạng phối cảnh của hình H 0
+ Hình H ’ là hình đồng dạng phối cảnh của hình H 0
+ Hình H đồng dạng của hình H 0
Có bao nhiêu khẳng định đúng?
Trong các hình con bướm dưới đây, có mấy hình là đồng dạng với nhau

Cho hai bức tranh như hình vẽ dưới đây:

Biết rằng bức tranh trong hình b là bức tranh trong hình a sau khi thu nhỏ với \(k = \frac{2}{3}.\) Nếu kích thước của bức tranh hình a là \(4 \times 6\) thì kích thước của bức tranh trong hình b là:
Hình bên dưới mô tả hai bức tranh kim tử tháp hình vuông những có kích thước khác nhau.

Biết rằng A, B, C, D lần lượt là trung điểm của OA’, OB’, OC’, OD’
Chọn đáp án đúng
Ba cái cây có hình vẽ như sau:

Cây 1 đồng dạng với cây 2 theo tỉ số là x.
Để cây 2 đồng dạng với cây 3 theo tỉ số đồng dạng là x thì:
Cho hai tem thư hình vuông như hình vẽ dưới đây:

Biết rằng tem thư 1 có diện tích là \(144c{m^2}\), tem thư 2 có chu vi là 40cm
Chọn đáp án đúng
Hình ảnh bên dưới là bức tranh Đông Hồ (hình chữ nhật) nhưng có kích thước khác nhau.

Biết rằng B, C, A, D lần lượt là trung điểm của OF, OG, OE, OH và diện tích của bức tranh ABCD bằng \(100c{m^2}\). Diện tích của bức tranh EFGH là:
Hai cái đĩa có mặt đĩa là hình tròn như hình sau:

Biết rằng mặt đĩa H có diện tích bằng \(113,04c{m^2}\). Mặt đĩa H’ là hình đồng dạng với mặt đĩa H có tỉ số đồng dạng bằng \(2\). Khi đó, diện tích của mặt đĩa H’ bằng:
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3.\) Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:

Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3\) nên tam giác A’B’C’ và tam giác ABC là đồng dạng phối cảnh với tỉ số vị tự là 3.
Do đó tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là \(\frac{1}{3}\).
Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) với tâm phối cảnh là:
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Chọn đáp án đúng nhất
Đáp án : C
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
+ Hai hình H, H’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Do đó, cả A và B đều đúng
Cho hình chữ nhật ba hình chữ nhật ABCD, A’B’C’D’, A”B”C”D” sao cho:
+ Hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh
+ Hình A”B”C”D” bằng hình A’B’C’D’
Chọn đáp án đúng
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng
Vì hai hình chữ nhật A”B”C”D” và ABCD là hai hình đồng dạng phối cảnh và hình A”B”C”D” bằng hình A’B’C’D’ nên
+ Hình A’B’C’D’ đồng dạng với hình ABCD
+ Hình A”B”C”D” đồng dạng với hình ABCD
Do đó, cả A, B đều đúng
Trong những cặp hình cho ở hình vẽ dưới đây, có mấy cặp hình là hình đồng dạng?

Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Các cặp hình đồng dạng là: Cặp hình 1 và cặp hình 2.
Vậy có 2 cặp hình đồng dạng.
Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA và OB.
Chọn đáp án đúng.
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.

Vì C là trung điểm của OA nên \(OC = \frac{1}{2}OA\)
Vì D là trung điểm của OB nên \(OD = \frac{1}{2}OB\)
Mà O là giao điểm của AC và BD nên cạnh CD là hình đồng dạng phối cảnh của cạnh AB với tỉ số đồng dạng \(k = \frac{1}{2}\), tâm phối cảnh là điểm O.
Do đó, cạnh CD là hình đồng dạng của cạnh AB với tỉ số \(k = \frac{1}{2}\)
Suy ra, cả A, B đều đúng.
Cho các hình vẽ sau:

Hình nào đồng dạng với hình a?
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì \(\frac{5}{5} \ne \frac{9}{{7,5}}\) nên hình a và hình b không phải là hai hình đồng dạng
Vì \(\frac{5}{{2,5}} = \frac{9}{{4,5}}\) nên hình a và hình c là hai hình đồng dạng với nhau
Vì \(\frac{{12}}{9} \ne \frac{4}{5}\) nên hình a và hình d không phải là hai hình đồng dạng
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng là: \(\frac{6}{3} = 2\)
Hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3.\) Nếu độ dài cạnh của hình vuông ABCD là 9cm thì độ dài cạnh của hình vuông A’B’C’D’ là:
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.
Vì hình vuông A’B’C’D’ là hình vuông ABCD sau khi phóng to với \(k = 3\) nên cạnh của hình vuông A’B’C’D’ gấp 3 lần cạnh của hình vuông ABCD. Do đó, cạnh của hình vuông A’B’C’D’ là: \(9.3 = 27\left( {cm} \right)\)
Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.

Cho các khẳng định sau:
+ Hình thang ABCD và EFGH bằng nhau
+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau
+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’
Có bao nhiêu khẳng định đúng?
Đáp án : D
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Hình thang ABCD và EFGH bằng nhau.
Vì các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD nên \(OA = 2OA',OB = 2OB',OC = 2OC',OD = 2OD'\).
Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’.
Do đó, hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau.
Vậy cả 3 khẳng định trên đều đúng
Cho tam giác ABC có AB = 4, BC = 7, CA = 6. Cho O, I là điểm phân biệt.
+ Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\)
+ Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{A'B'}{AB}=3\).
Chọn đáp án đúng
Đáp án : A
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh nên \(\frac{OA'}{OA}=\frac{OB'}{OB}=\frac{OC'}{OC}\) suy ra \( \Delta A'B'C'\backsim \Delta ABC\), do đó \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=3\)
suy ra \(A'B'=12;B'C'=21;C'A'=18\)
Vì tam giác A”B”C” là hình đồng dạng phối cảnh của tam giác ABC với I là tâm đồng dạng phối cảnh nên \(\frac{IA''}{IA}=\frac{IB''}{IB}=\frac{IC''}{IC}\) suy ra \( \Delta A''B''C''\backsim \Delta ABC\), do đó \(\frac{A''B''}{AB}=\frac{B''C''}{BC}=\frac{C''A''}{CA}=3\)
suy ra \(A''B''=12;B''C''=21;C''A''=18\)
Do đó, \(A'B'=A''B''=21,B'C'=B''C''=21,C'A'=C''A''=18\)
suy ra \(\frac{A''B''}{A'B'}=\frac{C''B''}{C'B'}=\frac{A''C''}{A'C'}=1\)
Cho tam giác ABC vuông tại A, gọi M là trung điểm của BC. Qua M vẽ đường thẳng vuông góc với AB cắt AB tại H.
Chọn đáp án đúng
Đáp án : A
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H ’bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)

Ta có: \(HM \bot AB,AC \bot AB\) nên HM//AC
Tam giác ABC có: M là trung điểm của BC, HM//AC nên H là trung điểm của AB.
Do đó, \(\frac{{BH}}{{BA}} = \frac{1}{2}\)
Lại có: Mà là trung điểm của BC nên \(\frac{{BM}}{{BC}} = \frac{1}{2}\)
Suy ra: \(\frac{{BH}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{2}\)
Mà đường thẳng AH và MC cùng đi qua điểm B.
Do đó, HM là hình đồng dạng phối cảnh của cạnh AC, tâm B, tỉ số \(\frac{1}{2}\)
Cho hai hình vuông EFGH, E’F’G’H’ lần lượt có độ dài cạnh là 10cm và 8cm.
Chọn câu trả lời đúng nhất
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H

Trên các đoạn thẳng EF, EG, EH, ta lần lượt lấy các điểm F”, G”, H” sao cho \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}.\) Theo định lý Thalès đảo ta có: F”G”//FG, G”H”//GH.
Mà \(\widehat{F''EH''}={{90}^{0}}\) nên tứ giác EF”G”H” là hình chữ nhật.
Mặt khác, ta có: \(\frac{EF''}{EF}=\frac{F''G''}{FG}=\frac{G''H''}{GH}=\frac{H''E}{HE}=\frac{4}{5}\) (hệ quả định lí Thalès)
Suy ra \(EF''=F''G''=G''H''=H''E=8cm\) .
Do đó, tứ giác EF”G”H” là hình vuông có độ dài cạnh bằng 8cm.
Suy ra, hai hình vuông EF”G”H” và E’F’G’H’ bằng nhau
Vì \(\frac{EF''}{EF}=\frac{EG''}{EG}=\frac{EH''}{EH}=\frac{4}{5}\) nên hình vuông EF”G”H” đồng dạng phối cảnh với hình vuông EFGH hay hình vuông E’F’G’H’ đồng dạng phối cảnh với hình vuông EFGH.
Vậy hình vuông E’F’G’H’ đồng dạng với hình vuông EFGH.
Tam giác ABC có chu vi bằng 18cm. Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\). Chu vi tam giác A’B’C’ bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Tam giác ABC có chu vi bằng 18cm nên \(AB + BC + CA = 18\)
Chu vi tam giác A’B’C’ là: \(P' = A'B' + A'C' + B'C'\)
Vì tam A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với O là tâm đồng dạng phối cảnh tỉ số \(\frac{{A'B'}}{{AB}} = \frac{1}{3}\) nên \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{3}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{{A'B' + A'C' + B'C'}}{{AB + AC + BC}} = \frac{{P'}}{{18}} = \frac{1}{3}\)
\( \Rightarrow P' = 18:3 = 6\left( {cm} \right)\)
Vậy chu vi tam giác A’B’C’ bằng 6cm
Hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD theo tỉ số đồng dạng k. Biết rằng diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\), diện tích hình vuông ABCD là \(36c{m^2}.\) Khi đó, tỉ số đồng dạng k bằng:
Đáp án : A
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H ’bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì diện tích hình vuông A’B’C’D’ bằng \(64c{m^2}\) nên ta có: \(A'B{'^2} = 64 \Rightarrow A'B' = 8cm\)
Vì diện tích hình vuông ABCD là \(36c{m^2}\) nên ta có: \(A{B^2} = 36 \Rightarrow AB = 6cm\)
Vì hình vuông A’B’C’D’ là hình đồng dạng với vuông ABCD tỉ số đồng dạng k nên:
\(k = \frac{{A'B'}}{{AB}} = \frac{8}{6} = \frac{4}{3}\)
Vậy tỉ số đồng dạng là \(\frac{4}{3}\)
Cho hình tròn H có diện tích bằng \(113,04c{m^2}\). Hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\). Khi đó, diện tích của hình tròn H’ bằng:
Đáp án : C
- Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H '
+ Hình H đồng dạng với hình H ’nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình tròn H có diện tích bằng \(113,04c{m^2}\) nên bán kính của hình tròn là: \({R^2} = \frac{{113,04}}{{3,14}} = 36 \Rightarrow R = 6cm\)
Vì hình tròn H’ là hình đồng dạng với hình H có tỉ số đồng dạng bằng \(\frac{1}{2}\) nên bán kính hình tròn H’ là: \(R' = \frac{R}{2} = 3\left( {cm} \right)\)
Diện tích hình tròn H’ là: \({3^2}.3,14 = 28,26c{m^2}\)
Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\). Biết rằng diện tích tam giác ABC bằng \(48c{m^2}.\) Diện tích tam giác AMN bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)

Vì đoạn thẳng MN là hình đồng dạng phối cảnh của đoạn thẳng BC tâm A, tỉ số đồng dạng \(\frac{1}{4}\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{4} \Rightarrow AB = 4AM,AC = 4AN\)
Diện tích tam giác AMN vuông tại A là: \({S_{AMN}} = \frac{1}{2}AM.AN\)
Vì tam giác ABC vuông tại A nên diện tích tam giác ABC là:
\(\frac{1}{2}AB.AC = 48 \Rightarrow \frac{1}{2}.4AM.4AN = 48 \Rightarrow \frac{1}{2}AM.AN = 3\left( {c{m^2}} \right)\)
Do đó, diện tích tam giác AMN bằng \(3c{m^2}\).
Cho tam giác ABC. Trên cạnh BC lấy điểm K sao cho \(CK = \frac{2}{3}BC.\) Tìm trên AB điểm H sao cho cạnh HK là hình đồng dạng phối cảnh của cạnh AC (với tâm đồng dạng phối cảnh là điểm B)
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)

Vì H thuộc AB và HK là hình đồng dạng phối cảnh của cạnh AC, với tâm đồng dạng phối cảnh là điểm B nên \(\frac{{HK}}{{AC}} = \frac{{BK}}{{BC}} = \frac{{BH}}{{BA}}\)
Mà \(CK = \frac{2}{3}BC \Rightarrow \frac{{BK}}{{BC}} = \frac{1}{3} \Rightarrow \frac{{BH}}{{BA}} = \frac{{KH}}{{AC}} = \frac{1}{3}\)
Do đó, điểm H cần tìm thuộc đoạn thẳng AB sao cho \(BH = \frac{1}{3}AB\).
: Cho hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 6cm,BC = 8cm,A'B' = 12cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ là:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k nên \(k = \frac{{A'B'}}{{AB}} = \frac{{12}}{6} = 2\)
Ta có: \(\frac{{B'C'}}{{BC}} = 2 \Rightarrow B'C' = 8.2 = 16\left( {cm} \right)\)
Diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 12.16 = 192\left( {c{m^2}} \right)\)
Cho tam giác ABC có \(AB = 3cm,BC = 4cm,AC = 5cm.\) Tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích tam giác A”B”C” bằng \(96c{m^2}\).
Chọn đáp án đúng
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2 nên \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=2\)
\(\Rightarrow A'B'=6cm,B'C'=8cm,A'C'=10cm\)
Vì \(A'C{{'}^{2}}=A'B{{'}^{2}}+B'C{{'}^{2}}\left( {{10}^{2}}={{8}^{2}}+{{6}^{2}} \right)\) nên tam giác A’B’C’ vuông tại B’
Vì tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x nên \(\Delta A''B''C''\backsim \Delta A'B'C'\)
Do đó, \(\widehat{A''B''C''}=\widehat{A'B'C'}=90\) và \(\frac{A''B''}{A'B'}=\frac{A''C''}{A'C'}=\frac{B''C''}{B'C'}=x\Rightarrow A''B''=6x,A''C''=10x,B''C''=8x\)
Vì tam giác A”B”C” vuông tại B” nên diện tích tam giác A”B”C” là:
\({{S}_{A''B''C''}}=\frac{1}{2}B''A''.B''C''\Rightarrow \frac{1}{2}.6x.8x=96\Rightarrow {{x}^{2}}=4\Rightarrow x=2\) (do \(x>0\))
Cho hình chữ nhật ABCD có \(AB = \frac{3}{4}BC.\) Hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD theo tỉ số đồng dạng 2. Biết rằng \(A'C' = 10cm.\) Khi đó, diện tích hình chữ nhật A’B’C’D’ bằng:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD có tỉ số đồng dạng 2 nên \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = 2\)
Mà \(AB = \frac{3}{4}BC \Rightarrow A'B' = \frac{3}{4}B'C'.\)
Vì A’B’C’D’ là hình chữ nhật nên \(\widehat {A'B'C'} = {90^0}\)
Do đó, tam giác A’B’C’ vuông tại B’. Áp dụng định lý Pytago vào tam giác A’B’C’ vuông tại B’ ta có: \(A'C{'^2} = A'B{'^2} + B'C{'^2}\) (1)
Thay \(A'B' = \frac{3}{4}B'C'\) vào (1) ta có:
\({\left( {\frac{3}{4}B'C'} \right)^2} + B'C{'^2} = {10^2}\)
\(\frac{{25}}{{16}}B'C{'^2} = 100\)
\(B'C{'^2} = 64\) nên \(B'C' = 8cm\)
Do đó, \(A'B' = 8.\frac{3}{4} = 6\left( {cm} \right)\)
Vậy diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 6.8 = 48\left( {c{m^2}} \right)\)
Cho hai tấm thảm hình tam giác ABC và A’B’C’, tấm thảm ABC có chu vi bằng 400cm và đồng dạng phối cảnh với tấm thảm A’B’C’ tâm O, tỉ số \(\frac{2}{3}.\) Chu vi tam giác A’B’C’ bằng:
Đáp án : B
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Chu vi tấm thảm ABC là: \(AB + BC + AC = 400\)
Chu vi tấm thảm A’B’C’ là: \(P' = A'B' + B'C' + A'C'\)
Vì tấm thảm ABC đồng dạng phối cảnh với tấm thảm A’B’C’ tâm O, tỉ số \(\frac{2}{3}\) nên ta có:
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{2}{3}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{{AB + BC + AC}}{{A'B' + B'C' + A'C'}} = \frac{{400}}{{P'}} = \frac{2}{3}\) nên \(P' = 400.\frac{3}{2} = 600\left( {cm} \right)\)
Một tủ sách nghệ thuật ở có dạng như hình vẽ sau:

Trong đó BM, CN, DP, EQ là các ngăn của tủ sách và ngăn EQ có độ dài 4m.
Có bao nhiêu khẳng định đúng trong các khẳng định sau?
+ Ngăn BM là hình đồng dạng phối cảnh với ngăn EQ, với tâm A, tỉ số bằng \(\frac{1}{4}\)
+ Ngăn CN là hình đồng dạng phối cảnh với ngăn DP, với tâm A, tỉ số bằng \(\frac{1}{3}\)
+ \(BM = 1m,CN = 2m,DP = 3m\)
Đáp án : C
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì \(\frac{{AM}}{{AQ}} = \frac{{AB}}{{AE}}\left( { = \frac{1}{4}} \right)\) và các đường thẳng BE và MQ cắt nhau tại A nên BM là hình đồng dạng phối cảnh với EQ, tâm A, tỉ số đồng dạng \(\frac{1}{4}\)
Vì \(\frac{{AC}}{{AD}} = \frac{{AN}}{{AP}}\left( { = \frac{2}{3}} \right)\) và các đường thẳng DC và NP cắt nhau tại A nên CN là hình đồng dạng phối cảnh với DP, tâm A, tỉ số đồng dạng \(\frac{2}{3}\)
Trong tam giác AQE có: \(\frac{{AM}}{{AQ}} = \frac{{AB}}{{AE}}\left( { = \frac{1}{4}} \right)\) nên BM//EQ.
Áp dụng hệ quả định lý Thalès vào tam giác AQE có:
\(\frac{{BM}}{{EQ}} = \frac{{AB}}{{AE}} \Rightarrow \frac{{BM}}{4} = \frac{1}{4} \Rightarrow BM = 1\left( m \right)\)
Trong tam giác AQE có: \(\frac{{AD}}{{AE}} = \frac{{AP}}{{AQ}}\left( { = \frac{3}{4}} \right)\) nên DP//EQ.
Theo hệ quả định lý Thalès vào tam giác AQE có:
\(\frac{{PD}}{{EQ}} = \frac{{AP}}{{AQ}} \Rightarrow \frac{{DP}}{4} = \frac{3}{4} \Rightarrow DP = 3\left( m \right)\)
Trong tam giác ADP có: \(\frac{{AC}}{{AD}} = \frac{{AN}}{{AP}}\left( { = \frac{2}{3}} \right)\) nên CN//DP.
Theo hệ quả định lý Thalès vào tam giác APD có:
\(\frac{{CN}}{{DP}} = \frac{{AC}}{{AD}} \Rightarrow \frac{{CN}}{3} = \frac{2}{3} \Rightarrow CN = 2\left( m \right)\)
Vậy có 2 khẳng định đúng
: Cho hai bức tranh hình chữ nhật như hình vẽ sau đây:

Cho bức tranh A’B’C’D’ là hình đồng dạng của bức tranh ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 12cm,BC = 16cm,A'B' = 24cm.\) Khi đó, diện tích bức tranh A’B’C’D’ là:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k nên \(k = \frac{{A'B'}}{{AB}} = \frac{{24}}{{12}} = 2\)
Ta có: \(\frac{{B'C'}}{{BC}} = 2 \Rightarrow B'C' = 16.2 = 32\left( {cm} \right)\)
Diện tích bức tranh A’B’C’D’ là: \(A'B'.B'C' = 24.32 = 768\left( {c{m^2}} \right)\)
Một chiếc khăn mặt có dạng hình tam giác ABC có \(AB = 12cm,BC = 16cm,AC = 20cm.\) Một chiếc khăn mặt khác hình tam giác A’B’C’ là hình đồng dạng phối cảnh của chiếc khăn ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Khăn tam giác A”B”C” là hình đồng dạng của khăn A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích chiếc khăn A”B”C” bằng \(1536c{m^2}\).
Chọn đáp án đúng
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2 nên \(\Delta A'B'C'\backsim \Delta ABC\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=2\)
\(\Rightarrow A'B'=24cm,B'C'=32cm,A'C'=40cm\)
Vì \(A'C{{'}^{2}}=A'B{{'}^{2}}+B'C{{'}^{2}}\left( {{40}^{2}}={{32}^{2}}+{{24}^{2}} \right)\) nên tam giác A’B’C’ vuông tại B’
Vì tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x nên \(\Delta A''B''C''\backsim \Delta A'B'C'\)
Do đó, \(\widehat{A''B''C''}=\widehat{A'B'C'}=90\) và \(\frac{A''B''}{A'B'}=\frac{A''C''}{A'C'}=\frac{B''C''}{B'C'}=x\Rightarrow A''B''=24x,A''C''=40x,B''C''=32x\)
Vì tam giác A”B”C” vuông tại B” nên diện tích tam giác A”B”C” là:
\({{S}_{A''B''C''}}=\frac{1}{2}B''A''.B''C''\Rightarrow \frac{1}{2}.24x.32x=1536\Rightarrow {{x}^{2}}=4\Rightarrow x=2\)(do \(x>0\))
Một mặt bàn hình chữ nhật ABCD có \(AB = \frac{5}{{12}}BC.\) Mặt bàn hình chữ nhật A’B’C’D’ là hình đồng dạng của mặt bàn hình chữ nhật ABCD có tỉ số đồng dạng 2. Biết rằng \(A'C' = 130cm.\) Khi đó, diện tích mặt bàn hình chữ nhật A’B’C’D’ bằng:
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD có tỉ số đồng dạng 2 nên \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = 2\)
Mà \(AB = \frac{5}{{12}}BC \Rightarrow A'B' = \frac{5}{{12}}B'C'.\)
Vì A’B’C’D’ là hình chữ nhật nên \(\widehat {A'B'C'} = {90^0}\)
Do đó, tam giác A’B’C’ vuông tại B’. Áp dụng định lý Pytago vào tam giác A’B’C’ vuông tại B’ ta có: \(A'C{'^2} = A'B{'^2} + B'C{'^2}\) (1)
Thay \(A'B' = \frac{5}{{12}}B'C'\) vào (1) ta có:
\({\left( {\frac{5}{{12}}B'C'} \right)^2} + B'C{'^2} = {130^2}\)
\(\frac{{169}}{{144}}B'C{'^2} = 16900\)
\(B'C{'^2} = 14400\) nên \(B'C' = 120cm\)
Do đó, \(A'B' = \frac{5}{{12}}.120 = 50\left( {cm} \right)\)
Vậy diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 50.120 = 6000\left( {c{m^2}} \right)\)
Trong các hình dưới đây, hình nào không thể hiện hình đồng dạng?

Đáp án : D
Các hình a, b, c đều thể hiện hình đồng dạng, chỉ có hình d là không thể hiện hình đồng dạng.
Cho hình cánh hoa:

Hình nào dưới đây đồng dạng với hình cánh hoa ở trên?



Đáp án : B
Trong các loài thực vật sau, loài thực vật nào thể hiện hình đồng dạng?



Đáp án : D
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Biển báo M là hình đồng dạng của biển báo P khi thu nhỏ với tỉ số k bằng:

Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Ta có: \(k = \frac{{4,8}}{{8,4}} = \frac{4}{7}\) nên biển báo M là hình đồng dạng của biển báo P khi thu nhỏ với tỉ số \(k = \frac{4}{7}\)
Cho các hình vẽ dưới đây:

Có bao nhiêu cặp hình đồng dạng trong các hình ở trên?
Không cặp hình nào
Đáp án : C
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Các cặp hình đồng dạng là: Hình a và hình c, hình b và hình d.
Vậy có 2 cặp hình đồng dạng.
Cho hình vẽ:

Cho các khẳng định sau:
+ Hình H là hình đồng dạng phối cảnh của hình H 0
+ Hình H ’ là hình đồng dạng phối cảnh của hình H 0
+ Hình H đồng dạng của hình H 0
Có bao nhiêu khẳng định đúng?
Đáp án : D
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
- Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng
Hình H là hình đồng dạng phối cảnh của hình H 0
Mà hình H ’ bằng với hình H 0 nên hình H đồng dạng của hình H 0
Vì hình H là hình đồng dạng phối cảnh của hình H 0 nên H là hình đồng dạng của hình H 0
Vậy cả ba khẳng định trên đều đúng
Trong các hình con bướm dưới đây, có mấy hình là đồng dạng với nhau

Đáp án : A
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì \(\frac{{4,5}}{3} = \frac{{3,9}}{{2,6}}\left( { = \frac{3}{2}} \right)\) nên hình b đồng dạng với hình a với tỉ số \(\frac{3}{2}\)
Vì \(\frac{{4,5}}{3} \ne \frac{{3,9}}{2}\) nên hai hình b và c không đồng dạng với nhau
Vì \(\frac{3}{3} \ne \frac{2}{{2,6}}\) nên hai hình a và c không đồng dạng với nhau
Cho hai bức tranh như hình vẽ dưới đây:

Biết rằng bức tranh trong hình b là bức tranh trong hình a sau khi thu nhỏ với \(k = \frac{2}{3}.\) Nếu kích thước của bức tranh hình a là \(4 \times 6\) thì kích thước của bức tranh trong hình b là:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì rằng bức tranh trong hình b là bức tranh trong hình a sau khi thu nhỏ với \(k = \frac{2}{3}\) nên kích thước ở hình b là: \(4.\frac{2}{3} = \frac{8}{3}\) và \(6.\frac{2}{3} = 4\)
Vậy kích thước của bức tranh trong hình b là: \(\frac{8}{3} \times 4\)
Hình bên dưới mô tả hai bức tranh kim tử tháp hình vuông những có kích thước khác nhau.

Biết rằng A, B, C, D lần lượt là trung điểm của OA’, OB’, OC’, OD’
Chọn đáp án đúng
Đáp án : A
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì A, B, C, D lần lượt là trung điểm của OA’, OB’, OC’, OD’ nên \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = \frac{{OD'}}{{OD}} = 2\)
Lại có các đường thẳng AA’, BB’, CC’, DD’ cùng đi qua điểm O.
Do đó, bức tranh A’B’C’D’ là hình đồng dạng phối cảnh của bức tranh ABCD, tâm đồng dạng phối cảnh là điểm O, tỉ số 2
Ba cái cây có hình vẽ như sau:

Cây 1 đồng dạng với cây 2 theo tỉ số là x.
Để cây 2 đồng dạng với cây 3 theo tỉ số đồng dạng là x thì:
Đáp án : C
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Cây 1 đồng dạng với cây 2 theo tỉ số là \(x = \frac{3}{2}\)
Để cây 2 đồng dạng với cây 3 theo tỉ số đồng dạng là \(\frac{3}{2}\) thì \(? = 2:\frac{3}{2} = \frac{4}{3}\left( m \right)\)
Cho hai tem thư hình vuông như hình vẽ dưới đây:

Biết rằng tem thư 1 có diện tích là \(144c{m^2}\), tem thư 2 có chu vi là 40cm
Chọn đáp án đúng
Đáp án : B
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Độ dài cạnh của tem thư 1 là: \(\sqrt {144} = 12\left( {cm} \right)\)
Độ dài cạnh của tem thư 2 là: \(40:4 = 10\left( {cm} \right)\)
Do đó, tem thư 1 là hình đồng dạng với tem thư 2 với tỉ số: \(\frac{{12}}{{10}} = \frac{6}{5}\)
Hình ảnh bên dưới là bức tranh Đông Hồ (hình chữ nhật) nhưng có kích thước khác nhau.

Biết rằng B, C, A, D lần lượt là trung điểm của OF, OG, OE, OH và diện tích của bức tranh ABCD bằng \(100c{m^2}\). Diện tích của bức tranh EFGH là:
Đáp án : A
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì B, C, A, D lần lượt là trung điểm của OF, OG, OE, OH nên \(\frac{{OB}}{{FO}} = \frac{{OA}}{{OE}} = \frac{{OD}}{{OH}} = \frac{{OC}}{{OG}} = \frac{1}{2}\) và các đường thẳng AD, EH, GC, FB cùng đi qua điểm O nên hình ABCD là hình đồng dạng phối cảnh với hình EFGH tâm O tỉ số \(\frac{1}{2}\).
Do đó, \(FG = 2BC,FE = 2AB\)
Diện tích bức tranh ABCD là: \(AB.BC = 100\left( {c{m^2}} \right)\)
Diện tích bức tranh EFGH là: \(FE.FG = 2AB.2BC = 4AB.BC = 4.100 = 400\left( {c{m^2}} \right)\)
Hai cái đĩa có mặt đĩa là hình tròn như hình sau:

Biết rằng mặt đĩa H có diện tích bằng \(113,04c{m^2}\). Mặt đĩa H’ là hình đồng dạng với mặt đĩa H có tỉ số đồng dạng bằng \(2\). Khi đó, diện tích của mặt đĩa H’ bằng:
Đáp án : D
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Vì mặt đĩa H có diện tích bằng \(113,04c{m^2}\) nên bán kính của mặt đĩa H là: \({R^2} = \frac{{113,04}}{{3,14}} = 36 \Rightarrow R = 6cm\)
Vì mặt đĩa H’ là hình đồng dạng với mặt đĩa H có tỉ số đồng dạng bằng 2 nên bán kính mặt đĩa H’ là: \(R' = 2R = 12\left( {cm} \right)\)
Diện tích mặt đĩa H’ là: \({12^2}.3,14 = 452,16\left( {c{m^2}} \right)\)
Bài 4: Hai hình đồng dạng trong chương trình Toán 8 Chân trời sáng tạo là một phần quan trọng trong việc xây dựng nền tảng kiến thức về hình học. Bài học này giới thiệu khái niệm về hai hình đồng dạng, các trường hợp đồng dạng của hai tam giác, và các tính chất liên quan. Việc nắm vững kiến thức này không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là cơ sở để học tập các kiến thức hình học nâng cao hơn.
Hai hình được gọi là đồng dạng với nhau nếu chúng có cùng hình dạng nhưng kích thước khác nhau. Điều này có nghĩa là một hình có thể được thu nhỏ hoặc phóng to để trở thành hình kia. Để hai hình đồng dạng, chúng phải thỏa mãn hai điều kiện sau:
Có ba trường hợp đồng dạng của hai tam giác:
Khi hai tam giác đồng dạng, chúng có những tính chất sau:
Kiến thức về hai hình đồng dạng có nhiều ứng dụng trong thực tế, chẳng hạn như:
Dưới đây là một số bài tập trắc nghiệm minh họa về Bài 4: Hai hình đồng dạng Toán 8 Chân trời sáng tạo:
Câu 1: Cho tam giác ABC và tam giác A'B'C' đồng dạng với nhau theo tỉ lệ k. Khẳng định nào sau đây là đúng?
Câu 2: Cho hai tam giác ABC và DEF có góc A = góc D và AB/DE = AC/DF. Khẳng định nào sau đây là đúng?
Câu 3: Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Gọi D là điểm sao cho tam giác ABC đồng dạng với tam giác ABD. Độ dài AD là bao nhiêu?
Chúc bạn học tốt và đạt kết quả cao trong các bài kiểm tra Toán 8!