Bài viết này trên giaitoan.edu.vn sẽ giúp các em học sinh lớp 5 hiểu rõ khái niệm về hình tam giác, các yếu tố của hình tam giác và cách tính diện tích hình tam giác một cách dễ dàng.
Chúng ta sẽ cùng nhau khám phá các loại tam giác khác nhau và áp dụng công thức tính diện tích vào giải các bài tập thực tế.
Hình tam giác có 3 cạnh bằng nhau gọi là hình tam giác đều.
Hình tam giác đều có 3 góc bằng nhau và cùng bằng 60°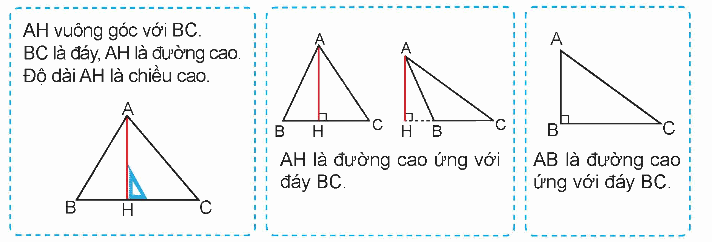
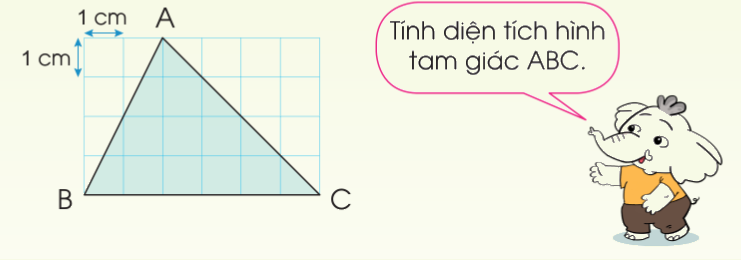
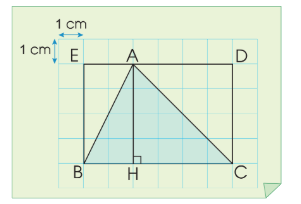
Vậy diện tích hình tam giác ABC bằng: \(\frac{{6 \times 4}}{2} = 12\) (cm2)
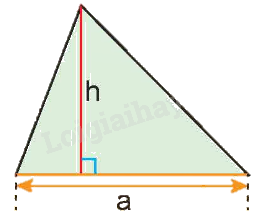
Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
S = $\frac{{a \times h}}{2}$
(S là diện tích, a là độ dài đáy, h là chiều cao)
Hình tam giác là một hình học phẳng được tạo thành bởi ba đoạn thẳng gọi là các cạnh. Ba đỉnh nơi các cạnh gặp nhau được gọi là các đỉnh của tam giác. Tam giác là một trong những hình cơ bản nhất trong hình học và xuất hiện trong nhiều lĩnh vực của toán học và cuộc sống.
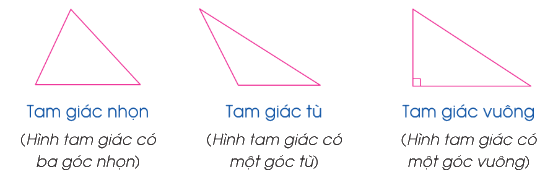
Có nhiều cách để phân loại tam giác dựa trên độ dài các cạnh và số đo các góc:
Diện tích hình tam giác là lượng không gian bên trong hình tam giác. Công thức tính diện tích hình tam giác là:
Diện tích = (1/2) * chiều cao * cạnh đáy
Trong đó:
Ví dụ 1: Một tam giác có cạnh đáy là 10cm và chiều cao là 5cm. Tính diện tích của tam giác này.
Giải:
Diện tích = (1/2) * 5cm * 10cm = 25cm2
Ví dụ 2: Một tam giác vuông có hai cạnh góc vuông là 6cm và 8cm. Tính diện tích của tam giác này.
Giải:
Diện tích = (1/2) * 6cm * 8cm = 24cm2
Ngoài công thức tính diện tích cơ bản, còn có các công thức khác để tính diện tích tam giác trong các trường hợp đặc biệt, chẳng hạn như:
Hy vọng bài viết này đã giúp các em học sinh lớp 5 hiểu rõ hơn về hình tam giác, các loại tam giác và cách tính diện tích hình tam giác. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài tập thực tế. Chúc các em học tốt!