Chào mừng các em học sinh lớp 8 đến với đề thi giữa kì 2 Toán 8 - Đề số 5 chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 2.
Giaitoan.edu.vn cung cấp đề thi và đáp án chi tiết, giúp các em tự học hiệu quả và đạt kết quả tốt nhất.
Phân thức \(\frac{2}{{x - 3}}\) không có nghĩa khi:
Cho \(\frac{{{{\left( {x + y} \right)}^2}}}{{x - y}} = \frac{P}{{{x^2} - {y^2}}}\). Đa thức P là:
Rút gọn phân thức \(\frac{{{x^3} - 2{x^2}}}{{2{x^2} - 4x}}\) ta được
Thương của hai phân thức \(\frac{{2x}}{{x - 3}}\) và \(\frac{{4{x^2}}}{{3 - x}}\) là:
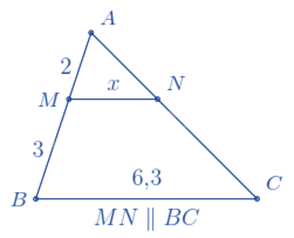
Cho hình vẽ sau, giá trị của x là:
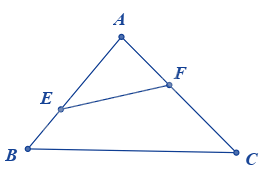
Cho ABC có AB = 24cm, AC = 30cm, BC = 36cm . Trên cạnh AB lấy E sao cho AE = 20cm . Trên cạnh AC lấy F sao cho AF = 16cm. Độ dài cạnh EF là
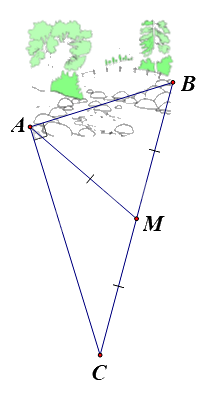
Ông An có một khu vườn, trong đó có miếng đất dạng hình tam giác vuông ABC như hình vẽ bên. Biết M là trung điểm của BC; AC = 40m; AM = 25m. Ông muốn trang trí lại khu vườn của mình nên cần biết khoảng cách từ A đến B. Em hãy giúp ông tính khoảng cách từ A đến B.
Cho $\Delta ABC\backsim \Delta HIK$, biết \(\widehat A = {80^0},\widehat B = {25^0}\). Khi đó số đo \(\widehat K\) bằng
1. Một vườn cây có \({x^2} + 2x - {y^2} - 2y\) cây, trong đó có \({x^2} - {y^2}\) cây lấy gỗ còn lại là cây ăn quả.
a) Viết phân thức biểu thị tỉ số cây lấy gỗ và số cây ăn quả.
b) Tính giá trị của phân thức đó tại \(x = 100;y = 10\).
2. Thực hiện phép tính:
a) \(\frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x - 4{x^2}}}\)
b) \(\frac{{{x^2} + x}}{{5{x^2} - 10x + 5}}:\frac{{3x + 3}}{{5x - 5}}\)
Cho các biểu thức \(P = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{{2x + 10}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\); \(Q = \frac{{x - 4}}{{{x^2} - 25}}\) với \(x \ne \pm 5\).
a) Tính giá trị Q với \(x = 6\).
b) Rút gọn biểu thức P.
c) Đặt \(A = \frac{Q}{P}\). Tìm các giá trị nguyên của x để A nhận giá trị nguyên.
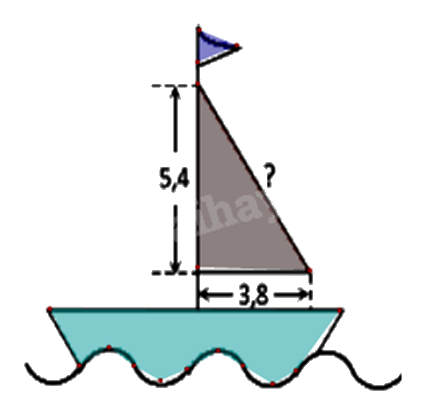
Cho hình vẽ bên. Tính chiều dài của cánh buồm?
(Làm tròn đến hàng phần trăm).
Cho tam giác ABC có ba góc nhọn. Đường cao AF, BE cắt nhau tại H. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By vuông góc với BC. Tia Ax và By cắt nhau tại K.
a) Tứ giác AHBK là hình gì? Vì sao?
b) Chứng minh $\Delta HAE\backsim \Delta HBF$.
c) Chứng minh \(CE.CA = CF.CB\).
d) \(\Delta ABC\) cần thêm điều kiện gì để tứ giác AHBK là hình thoi.
Cho a, b, c và x, y, z là các số khác nhau và khác 0. Chứng minh rằng:
Nếu \(\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0\) và \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) thì \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\).
Phân thức \(\frac{2}{{x - 3}}\) không có nghĩa khi:
Đáp án : A
Phân thức \(\frac{A}{B}\) có nghĩa khi \(B \ne 0\) nên phân thức \(\frac{A}{B}\) không có nghĩa khi \(B = 0\).
Phân thức \(\frac{2}{{x - 3}}\) có nghĩa khi \(x - 3 = 0\) hay \(x = 3\).
Cho \(\frac{{{{\left( {x + y} \right)}^2}}}{{x - y}} = \frac{P}{{{x^2} - {y^2}}}\). Đa thức P là:
Đáp án : C
Sử dụng kiến thức về hai phân thức bằng nhau.
Ta có: \(\frac{{{{\left( {x + y} \right)}^2}}}{{x - y}} = \frac{P}{{{x^2} - {y^2}}}\)
\(\begin{array}{l} \Rightarrow {\left( {x + y} \right)^2}.\left( {{x^2} - {y^2}} \right) = P.\left( {x - y} \right)\\{\left( {x + y} \right)^2}.\left( {x + y} \right)\left( {x - y} \right) = P.\left( {x - y} \right)\\{\left( {x + y} \right)^3}\left( {x - y} \right) = P\left( {x - y} \right)\\ \Rightarrow P = {\left( {x + y} \right)^3}\end{array}\)
Rút gọn phân thức \(\frac{{{x^3} - 2{x^2}}}{{2{x^2} - 4x}}\) ta được
Đáp án : C
Thực hiện rút gọn phân thức theo 2 bước:
+ Bước 1: Phân tích tử và mẫu thành nhân tử (nếu cần).
+ Bước 2: Tìm nhân tử chung của tử và mẫu rồi chia cả tử và mẫu cho nhân tử chung đó.
Ta có: \(\frac{{{x^3} - 2{x^2}}}{{2{x^2} - 4x}} = \frac{{{x^2}\left( {x - 2} \right)}}{{2x\left( {x - 2} \right)}} = \frac{x}{2}\).
Thương của hai phân thức \(\frac{{2x}}{{x - 3}}\) và \(\frac{{4{x^2}}}{{3 - x}}\) là:
Đáp án : B
Sử dụng quy tắc chia hai phân thức.
Ta có: \(\frac{{2x}}{{x - 3}}:\frac{{4{x^2}}}{{3 - x}} = \frac{{2x}}{{x - 3}}.\frac{{3 - x}}{{4{x^2}}} = \frac{{2x}}{{x - 3}}.\frac{{ - \left( {x - 3} \right)}}{{4{x^2}}} = \frac{{ - 2x}}{{4{x^2}}} = \frac{{ - 1}}{{2x}}\).
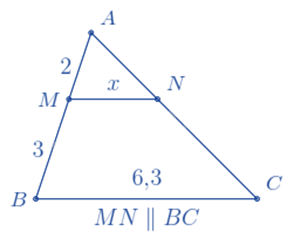
Cho hình vẽ sau, giá trị của x là:
Đáp án : A
Dựa vào định lí hai tam giác đồng dạng.
Ta có: MN // BC nên $\Delta AMN\backsim \Delta ABC$ (định lí hai tam giác đồng dạng)
\( \Rightarrow \frac{{AM}}{{AB}} = \frac{{MN}}{{BC}} \Rightarrow \frac{2}{{2 + 3}} = \frac{x}{{6,3}} \Rightarrow x = 6,3.\frac{2}{5} = 2,52\).
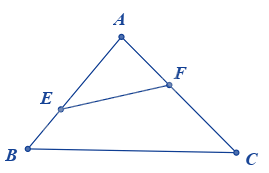
Cho ABC có AB = 24cm, AC = 30cm, BC = 36cm . Trên cạnh AB lấy E sao cho AE = 20cm . Trên cạnh AC lấy F sao cho AF = 16cm. Độ dài cạnh EF là
Đáp án : C
Chứng minh $\Delta AEF\backsim \Delta ACB$ suy ra tỉ số đồng dạng.
Xét \(\Delta AEF\) và \(\Delta ACB\) có:
\(\widehat A\) chung
\(\frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}\left( {\frac{{20}}{{16}} = \frac{{30}}{{24}} = \frac{5}{4}} \right)\)
$\Rightarrow \Delta AEF\backsim \Delta ACB\left( c.g.c \right)$
\(\begin{array}{l}\frac{{AE}}{{AC}} = \frac{{EF}}{{BC}}\\\frac{{20}}{{30}} = \frac{{EF}}{{36}}\\ \Rightarrow EF = 36.\frac{{20}}{{30}} = 24\end{array}\)
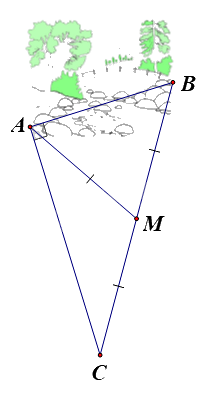
Ông An có một khu vườn, trong đó có miếng đất dạng hình tam giác vuông ABC như hình vẽ bên. Biết M là trung điểm của BC; AC = 40m; AM = 25m. Ông muốn trang trí lại khu vườn của mình nên cần biết khoảng cách từ A đến B. Em hãy giúp ông tính khoảng cách từ A đến B.
Đáp án : C
Sử dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác để tính BC, định lí Pythagore để tính AB.
Vì tam giác ABC vuông tại A và M là trung điểm của BC nên AM là đường trung tuyến ứng với cạnh huyền trong tam giác ABC.
\( \Rightarrow AM = \frac{1}{2}BC \Rightarrow BC = 2AM = 2.25 = 50\left( m \right)\)
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
\(\begin{array}{l}A{B^2} = B{C^2} - A{C^2} = {50^2} - {40^2} = {30^2}\\ \Rightarrow AB = 30\left( m \right)\end{array}\)
Cho $\Delta ABC\backsim \Delta HIK$, biết \(\widehat A = {80^0},\widehat B = {25^0}\). Khi đó số đo \(\widehat K\) bằng
Đáp án : C
Sử dụng đặc điểm của hai tam giác đồng dạng.
Vì $\Delta ABC\backsim \Delta HIK$ nên \(\widehat A = \widehat H;\widehat B = \widehat I;\widehat C = \widehat K\)
\( \Rightarrow \widehat C = \widehat K = {180^0} - \widehat A - \widehat B = {180^0} - {80^0} - {25^0} = {75^0}\).
1. Một vườn cây có \({x^2} + 2x - {y^2} - 2y\) cây, trong đó có \({x^2} - {y^2}\) cây lấy gỗ còn lại là cây ăn quả.
a) Viết phân thức biểu thị tỉ số cây lấy gỗ và số cây ăn quả.
b) Tính giá trị của phân thức đó tại \(x = 100;y = 10\).
2. Thực hiện phép tính:
a) \(\frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x - 4{x^2}}}\)
b) \(\frac{{{x^2} + x}}{{5{x^2} - 10x + 5}}:\frac{{3x + 3}}{{5x - 5}}\)
1. Sử dụng quy tắc trừ đa thức để tính số cây ăn quả.
a) Viết phân thức có số cây lấy gỗ là tử và số cây ăn quả là mẫu.
b) Thay x = 100 và y = 10 vào phân thức để tính giá trị.
2. Sử dụng các quy tắc tính với phân thức để tính.
1. Số cây ăn quả là:
\(\begin{array}{l}{x^2} + 2x - {y^2} - 2y - \left( {{x^2} - {y^2}} \right)\\ = {x^2} + 2x - {y^2} - 2y - {x^2} + {y^2}\\ = \left( {{x^2} - {x^2}} \right) + \left( { - {y^2} + {y^2}} \right) + 2x - 2y\\ = 2x - 2y\end{array}\)
a) Phân thức biểu thị tỉ số cây lấy gỗ và số cây ăn quả là: \(\frac{{{x^2} - {y^2}}}{{2x - 2y}}\).
b) Ta có: \(\frac{{{x^2} - {y^2}}}{{2x - 2y}} = \frac{{\left( {x - y} \right)\left( {x + y} \right)}}{{2\left( {x - y} \right)}} = \frac{{x + y}}{2}\).
Thay \(x = 100;y = 10\) vào phân thức ta được: \(\frac{{100 + 10}}{2} = \frac{{110}}{2}\).
2.
a) \(\frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x - 4{x^2}}}\) (ĐK: \(x \ne 0;x \ne \frac{1}{2}\))
\(\begin{array}{l} = \frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{\left( {1 - 3x} \right)\left( {1 - 2x} \right)}}{{2x\left( {1 - 2x} \right)}} - \frac{{2x\left( {3x - 2} \right)}}{{2x\left( {1 - 2x} \right)}} + \frac{{3x - 2}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{1 - 5x + 6{x^2} - 6{x^2} + 4x + 3x - 2}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{2x - 1}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{ - 1}}{{2x}}\end{array}\)
b) \(\frac{{{x^2} + x}}{{5{x^2} - 10x + 5}}:\frac{{3x + 3}}{{5x - 5}}\) (ĐK: \(x \ne 1\))
\(\begin{array}{l} = \frac{{x\left( {x + 1} \right)}}{{5\left( {{x^2} - 2x + 1} \right)}}.\frac{{5\left( {x - 1} \right)}}{{3\left( {x + 1} \right)}}\\ = \frac{{x\left( {x + 1} \right).5\left( {x - 1} \right)}}{{5{{\left( {x - 1} \right)}^2}.3\left( {x + 1} \right)}}\\ = \frac{x}{{3\left( {x - 1} \right)}}\end{array}\)
Cho các biểu thức \(P = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{{2x + 10}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\); \(Q = \frac{{x - 4}}{{{x^2} - 25}}\) với \(x \ne \pm 5\).
a) Tính giá trị Q với \(x = 6\).
b) Rút gọn biểu thức P.
c) Đặt \(A = \frac{Q}{P}\). Tìm các giá trị nguyên của x để A nhận giá trị nguyên.
a) Kiểm tra điều kiện của x, nếu thỏa mãn thì thay giá trị của x vào Q để tính Q.
b) Sử dụng các quy tắc tính với phân thức để rút gọn P.
c) Tính \(A = \frac{Q}{P}\). Để A nguyên thì tử thức chia hết cho mẫu thức.
a) Ta có x = 6 thỏa mãn điều kiện nên thay x = 6 vào Q, ta được:
\(Q = \frac{{6 - 4}}{{{6^2} - 25}} = \frac{2}{{11}}\)
Vậy \(Q = \frac{2}{{11}}\) với \(x = 6\).
b) Ta có:
\(\begin{array}{l}P = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{{2x + 10}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\\ = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{{2\left( {x + 5} \right)}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\\ = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{2}{{x - 5}}\\ = \frac{1}{{x + 5}}\end{array}\)
Vậy \(P = \frac{1}{{x + 5}}\).
c) Ta có:
\(\begin{array}{l}A = \frac{Q}{P} = \frac{1}{{x + 5}}:\frac{{x - 4}}{{{x^2} - 25}}\\ = \frac{1}{{x + 5}}.\frac{{\left( {x - 5} \right)\left( {x + 5} \right)}}{{x - 4}}\\ = \frac{{x - 5}}{{x - 4}}\end{array}\)
\(A = \frac{{x - 5}}{{x - 4}} = \frac{{x - 4 - 1}}{{x - 4}} = 1 - \frac{1}{{x - 4}}\).
Để A nguyên thì \(\frac{1}{{x - 4}}\) là số nguyên hay \(1 \vdots \left( {x - 4} \right)\) \( \Rightarrow \left( {x - 4} \right) \in \) Ư(1); Ư(1) = \(\left\{ { \pm 1} \right\}\).
Với x – 4 = 1 \( \Rightarrow \) x = 5 (không thỏa mãn)
Với x – 4 = -1 \( \Rightarrow \) x = 3 (thỏa mãn)
Vậy với x = 3 thì A nguyên.
Cho hình vẽ bên. Tính chiều dài của cánh buồm?
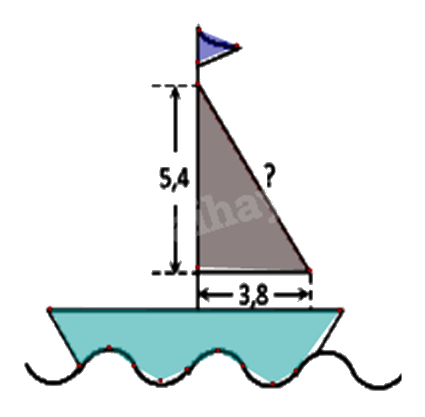
(Làm tròn đến hàng phần trăm).
Áp dụng Định lí Pythagore để tính chiều dài của cánh buồm.
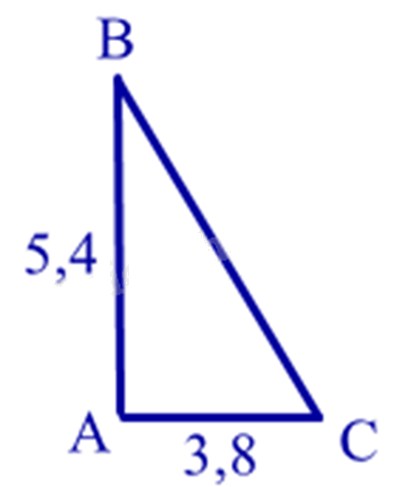
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} = 5,{4^2} + 3,{8^2} = 43,6\\ \Rightarrow BC = 6,60\end{array}\)
Vậy chiều dài cánh buồm là 6,6.
Cho tam giác ABC có ba góc nhọn. Đường cao AF, BE cắt nhau tại H. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By vuông góc với BC. Tia Ax và By cắt nhau tại K.
a) Tứ giác AHBK là hình gì? Vì sao?
b) Chứng minh $\Delta HAE\backsim \Delta HBF$.
c) Chứng minh \(CE.CA = CF.CB\).
d) \(\Delta ABC\) cần thêm điều kiện gì để tứ giác AHBK là hình thoi.
a) Chứng minh AHBK có hai cặp cạnh đối song song nên là hình bình hành.
b) Chứng minh $\Delta HAE\backsim \Delta HBF$ theo trường hợp góc – góc.
c) Chứng minh $\Delta AFC\backsim \Delta BEC$ (g.g) để chứng minh \(CE.CA = CF.CB\).
d) Gọi D là giao điểm KH và AB
Để tứ giác AHBK là hình thoi thì KH vuông góc AB
Ta có: H là trực tâm \( \Rightarrow \) CH vuông góc AB
\( \Rightarrow \) C, H, D thẳng hàng \( \Rightarrow \) CD là đường cao và D là trung điểm của AB \( \Rightarrow \) CD cũng là đường trung tuyến
\( \Rightarrow \) Tam giác ABC cân tại C
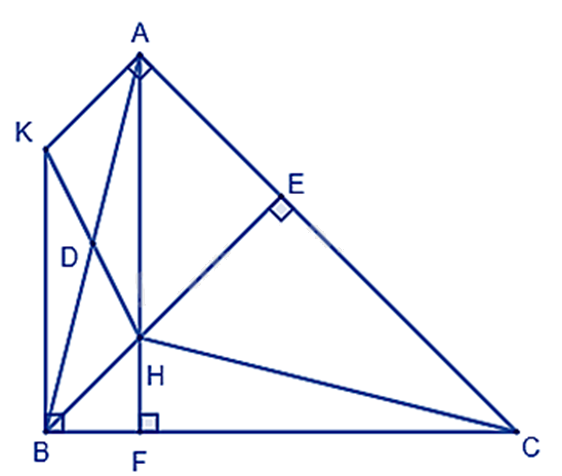
a) Ta có:
\(\left. \begin{array}{l}AK \bot AC\\BE \bot AC\end{array} \right\} \Rightarrow AK//BE\)
\(\left. \begin{array}{l}BK \bot BC\\AF \bot BC\end{array} \right\} \Rightarrow BK//AF\)
Xét tứ giác AHBK có:
\(\begin{array}{l}AK//BH\left( {H \in BE} \right)\\AB//AH\left( {H \in AF} \right)\end{array}\)
\( \Rightarrow \) AHBK là hình bình hành.
b) Xét \(\Delta HAE\) và \(\Delta HBF\) có:
\(\widehat E = \widehat F\left( { = {{90}^0}} \right)\)
\(\widehat {AHE} = \widehat {BHF}\) (hai góc đối đỉnh)
$\Rightarrow \Delta HAE\backsim \Delta HBF$ (g.g) (đpcm)
c) Xét \(\Delta AFC\) và \(\Delta BEC\) có:
\(\widehat F = \widehat E\left( { = {{90}^0}} \right)\)
\(\widehat C\) chung
$\Rightarrow \Delta AFC\backsim \Delta BEC\left( g.g \right)$
\( \Rightarrow \frac{{AC}}{{BC}} = \frac{{CF}}{{CE}} \Rightarrow AC.CE = CF.CB\) (đpcm)
d) Gọi D là giao điểm của AB và HK \( \Rightarrow \) D là trung điểm của AB và HK.
Để AHBK là hình thoi thì \(AB \bot HK\).
Mà H trực tâm của tam giác ABC nên \(CH \bot AB\).
\( \Rightarrow \) C, H, K thẳng hàng hay C, H, D thẳng hàng.
Khi đó CD là đường cao của tam giác ABC.
Mà D là trung điểm của AB nên CD cũng là đường trung tuyến của tam giác ABC
\( \Rightarrow \) Tam giác ABC cân tại C.
Vậy để AHBK là hình thoi thì tam giác ABC cân tại C.
Cho a, b, c và x, y, z là các số khác nhau và khác 0. Chứng minh rằng:
Nếu \(\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0\) và \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) thì \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\).
Biến đổi \(\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0\) và \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) để có đpcm.
Sử dụng hằng đẳng thức nâng cao: \({\left( {A + B + C} \right)^2} = {A^2} + {B^2} + {C^2} + 2AB + 2AC + 2BC\).
Ta có:
\(\begin{array}{l}\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0\\\frac{{ayz + bxz + cxy}}{{xyz}} = 0\\ \Rightarrow ayz + bxz + cxy = 0\end{array}\)
Ta lại có:
\(\begin{array}{l}\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\\ \Rightarrow {\left( {\frac{x}{a} + \frac{y}{b} + \frac{z}{c}} \right)^2} = 1\\{\left( {\frac{x}{a}} \right)^2} + {\left( {\frac{y}{b}} \right)^2} + {\left( {\frac{z}{c}} \right)^2} + 2.\frac{x}{a}.\frac{y}{b} + 2.\frac{x}{a}.\frac{z}{c} + 2.\frac{y}{b}.\frac{z}{c} = 1\\{\left( {\frac{x}{a}} \right)^2} + {\left( {\frac{y}{b}} \right)^2} + {\left( {\frac{z}{c}} \right)^2} + 2\left( {\frac{{xy}}{{ab}} + \frac{{xz}}{{ac}} + \frac{{yz}}{{bc}}} \right) = 1\\\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} + 2\left( {\frac{{xyc + bxz + ayz}}{{abc}}} \right) = 1\\\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} + 2.\frac{0}{{abc}} = 1\\\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\end{array}\)
Ta được điều phải chứng minh.
Đề thi giữa kì 2 Toán 8 - Đề số 5 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong học kì. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như đa thức, phân thức đại số, phương trình bậc nhất một ẩn, hệ phương trình bậc nhất hai ẩn, bất phương trình bậc nhất một ẩn, và ứng dụng thực tế của các kiến thức này.
Thông thường, đề thi giữa kì 2 Toán 8 - Đề số 5 có cấu trúc gồm các phần sau:
Phần này thường bao gồm các bài tập về:
Các bài tập thường gặp:
Các dạng bài tập:
Các bài tập liên quan đến:
Để giải đề thi giữa kì 2 Toán 8 - Đề số 5 hiệu quả, học sinh cần:
Việc luyện tập với đề thi giữa kì 2 Toán 8 - Đề số 5 mang lại nhiều lợi ích cho học sinh:
Giaitoan.edu.vn là một website cung cấp các tài liệu học Toán 8 uy tín và chất lượng, bao gồm:
Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu hữu ích và đồng hành cùng chúng tôi trên con đường chinh phục môn Toán!