Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 10, được biên soạn theo chuẩn chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ toàn bộ kiến thức trọng tâm của chương trình học kì 2 Toán 8 Kết nối tri thức.
Rút gọn biểu thức \(\frac{{5{x^2} - 10xy}}{{2{{\left( {x - 2y} \right)}^3}}}\) được kết quả bằng
\(\frac{{5x}}{{2{{\left( {x - 2y} \right)}^2}}}\).
\(\frac{{5xy}}{{2{{\left( {x - 2y} \right)}^2}}}\).
\(\frac{{5x}}{{{{\left( {x - 2y} \right)}^2}}}\).
\(\frac{5}{{2{{\left( {x - 2y} \right)}^2}}}\).
Phân thức đối của phân thức \(\frac{{ - 2y}}{{5{x^3}}}\) là:
\( - \frac{{2y}}{{5{x^3}}}\).
\(\frac{{2y}}{{5{x^3}}}\).
\( - \frac{{5{x^3}}}{{2y}}\).
\(\frac{{5{x^3}}}{{2y}}\).
Mẫu thức chung của hai phân thức \(\frac{3}{{2{x^3}{y^4}}}\) và \(\frac{4}{{5{x^4}{y^3}}}\) là
\(10{x^4}{y^4}\).
\(10{x^4}{y^3}\).
\(10{x^3}{y^3}\).
\({x^4}{y^4}\).
Kết quả rút gọn của biểu thức \(\frac{{{x^2} + 4x + 4}}{{9 - {{\left( {x + 5} \right)}^2}}}\) bằng
\(\frac{{x + 2}}{{8 - x}}\).
\(\frac{{ - x - 2}}{{x + 8}}\).
\(\frac{{x + 2}}{{x - 8}}\).
\(\frac{{x + 2}}{{x + 8}}\).
Kết quả của phép tính \(\frac{{x{y^2}}}{{xy}} + \frac{{{x^2}y}}{{xy}}\) bằng
\({\left( {xy} \right)^2}\).
\(xy\).
\(2x{y^2}\).
\(x + y\).
Phân thức \(K\left( x \right)\) thỏa mãn \(K\left( x \right):\frac{x}{{4 - x}} = \frac{{4 - x}}{2}\) là
\(\frac{{4 - x}}{{x - 2}}\).
\(\frac{2}{x}\).
\(\frac{x}{2}\).
\(\frac{{x - 2}}{4}\).
Cho $\Delta GHI\backsim \Delta FEI$ có các kính thước như hình vẽ, khi đó tỉ số độ dài của \(x\) và \(y\) bằng:

6.
2.
3.
\(\frac{1}{2}\).
Cho hình thang vuông ABCD (\(\widehat A = \widehat D = 90^\circ \)) có \(DB \bot BC\), AB = 4cm, CD = 9cm. Độ dài đoạn thẳng BD là:
6cm.
8cm.
9cm.
12cm.
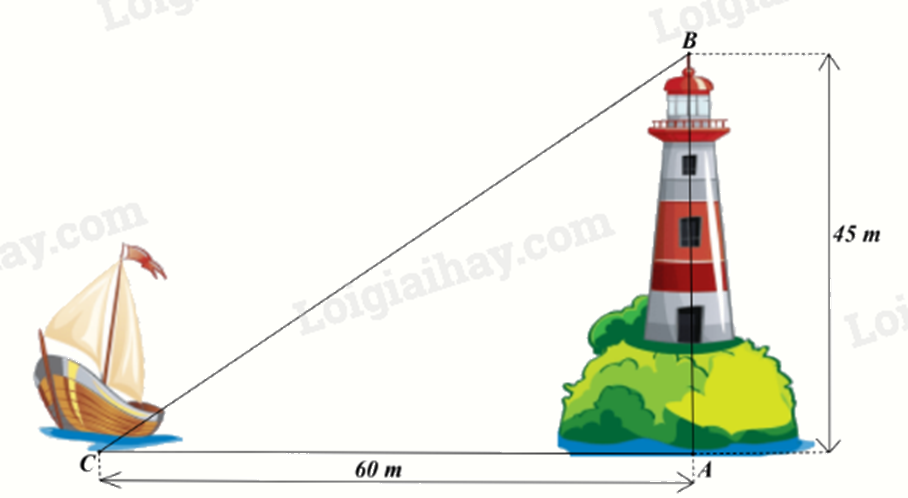
Ngọn hải đăng Lý Sơn (thuộc tỉnh Quảng Ngãi) cao 45m. Một con tàu đậu cách chân ngọn hải đăng 60m. Khoảng cách từ tàu đến đỉnh ngọn hải đăng là
75m.
105m.
85m.
55m.
Cho tam giác \(ABC\), điểm \(M\) thuộc cạnh \(BC\) sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\). Đường thẳng đi qua \(M\) và song song với \(AC\) cắt \(AB\) ở \(D\). Đường thẳng đi qua \(M\) và song song với \(AB\) cắt \(AC\) ở \(E\). Tỉ số chu vi hai tam giác \(\Delta DBM\) và \(\Delta EMC\) là
\(\frac{2}{3}\).
\(\frac{1}{2}\).
\(\frac{1}{4}\).
\(\frac{1}{3}\).
Cho \(\Delta ABC\) và \(\Delta MNP\) có: \(\widehat A = \widehat M = 90^\circ \). Để kết luận $\Delta ABC\backsim \Delta MNP$ theo trường hợp cạnh huyền – cạnh góc vuông thì cần có thêm điều kiện nào sau đây
\(\widehat B = \widehat N\).
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\).
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\).
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{MP}}\).
Trong các hình sau hình nào có 2 hình đồng dạng

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho biểu thức \(A = \left( {\frac{{{x^2} + 1}}{{{x^2} + x}} + \frac{2}{{x + 1}}} \right):\frac{{{{\left( {x + 1} \right)}^2}}}{{2x}}\) với \(x \ne 0;{\mkern 1mu} {\mkern 1mu} x \ne - 1\).
a) Rút gọn biểu thức A ta được kết quả \(A = - \frac{2}{{x + 1}}\).
b) Khi \(x = - 1\) thì giá trị biểu thức là 2.
c) Biểu thức \(A = 1\) khi \(x = 1\).
d) Để \(A \in \mathbb{Z}\) thì \(x \in \left\{ { - 3; - 2;1;0} \right\}\).
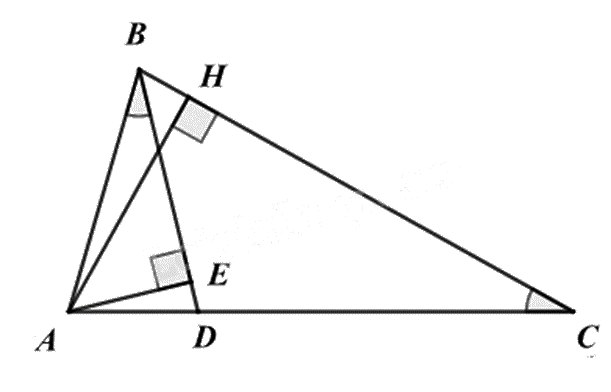
Cho \(\Delta ABC\) có AB = 2cm, AC = 4cm. Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\). Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\).
a) $\Delta ABD\backsim \Delta ACB$.
b) \(\widehat {ADB} = \widehat {ABC}\).
c) \(AD = 0,5cm,DC = 3,5cm\).
d) \({S_{\Delta ABH}} = 4{S_{\Delta ADE}}\).
Cho phân thức \(H\left( x \right)\) thỏa mãn \(\frac{x}{{3 - x}} - H\left( x \right) = \frac{2}{{3 - x}}\). Giá trị của \(H\left( x \right)\) tại \(x = 2\) là.
Đáp án:
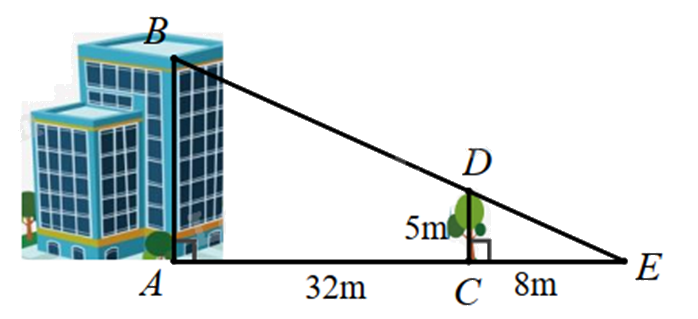
Biết cái cây có chiều cao \(CD = 5m\) và khoảng cách \(AC = 32m\), \(EC = 8m\). Chiều cao \(AB\) của ngôi nhà là …m.
Đáp án:
Một chiếc ti vi 24 inch có nghĩa là đường chéo màn hình của nó có độ dài là 24 inch (inch: đơn vị đo độ dài sử dụng ở nước Anh và một số nước khác, 1 inch \( \approx \) 2,54cm). Biết một ti vi màn hình phẳng có chiều dài, chiều rộng của màn hình lần lượt là 14,8 inch và 11,8 inch thì tivi đó thuộc loại bao nhiêu inch? (làm tròn đến chữ số thập phân thứ nhất)

Đáp án:
Tổng các giá trị của y để biểu thức \(\frac{{1 + {y^2} + \frac{1}{y}}}{{2 + \frac{1}{y}}}\) bằng 1 là
Đáp án:
a) Thực hiện phép tính: \(\frac{1}{{2\left( {x + 3} \right)}} + \frac{3}{{2x\left( {x + 3} \right)}}\).
b) Tìm đa thức A thỏa mãn \(\frac{A}{{x - 2}} = \frac{{2{x^3} + 4{x^2}}}{{{x^2} - 4}}\), \(x \ne \pm 2\).
Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh $\Delta ABC\backsim \Delta HBA$.
b) Tia phân giác của góc AHC cắt AC tại D. Chứng minh \(\frac{{HB}}{{HC}} = \frac{{A{D^2}}}{{D{C^2}}}\).
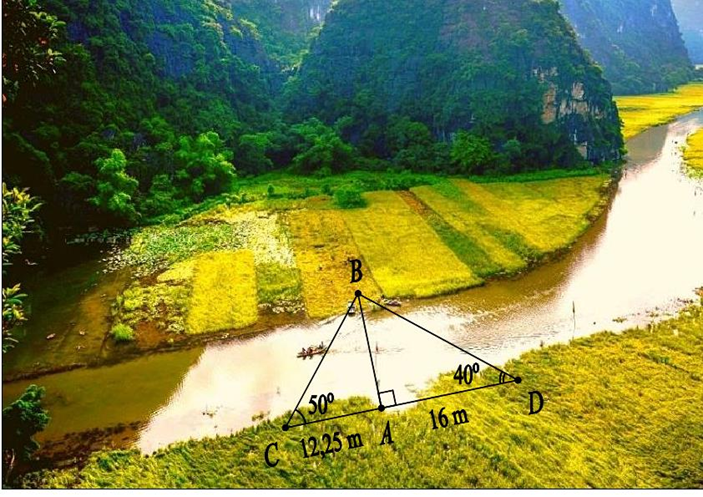
Một người tiến hành đo khoảng cách từ điểm A bên này sông đến điểm B bên kia sông như hình vẽ sau. Người đó vạch trên bờ sông một đường thẳng d đi qua A và vuông góc với đường thẳng AB, sau đó xác định hai điểm C và D sao cho \(\widehat {ACB} = 50^\circ \) và \(\widehat {ADC} = 40^\circ \). Người đó đo được \(AC = 12,25m;AD = 16m\). Tính khoảng cách AB.
Rút gọn biểu thức \(\frac{{5{x^2} - 10xy}}{{2{{\left( {x - 2y} \right)}^3}}}\) được kết quả bằng
\(\frac{{5x}}{{2{{\left( {x - 2y} \right)}^2}}}\).
\(\frac{{5xy}}{{2{{\left( {x - 2y} \right)}^2}}}\).
\(\frac{{5x}}{{{{\left( {x - 2y} \right)}^2}}}\).
\(\frac{5}{{2{{\left( {x - 2y} \right)}^2}}}\).
Đáp án : A
Chia cả tử và mẫu thức của biểu thức cho nhân tử chung.
Ta có: \(\frac{{5{x^2} - 10xy}}{{2{{\left( {x - 2y} \right)}^3}}} = \frac{{5x\left( {x - 2y} \right)}}{{2{{\left( {x - 2y} \right)}^3}}} = \frac{{5x}}{{2{{\left( {x - 2y} \right)}^2}}}\)
Đáp án A
Phân thức đối của phân thức \(\frac{{ - 2y}}{{5{x^3}}}\) là:
\( - \frac{{2y}}{{5{x^3}}}\).
\(\frac{{2y}}{{5{x^3}}}\).
\( - \frac{{5{x^3}}}{{2y}}\).
\(\frac{{5{x^3}}}{{2y}}\).
Đáp án : B
Phân thức đối của phân thức \(\frac{A}{B}\) là \( - \frac{A}{B}\).
Phân thức đối của phân thức \(\frac{{ - 2y}}{{5{x^3}}}\) là \( - \left( {\frac{{ - 2y}}{{5{x^3}}}} \right) = \frac{{2y}}{{5{x^3}}}\).
Đáp án B
Mẫu thức chung của hai phân thức \(\frac{3}{{2{x^3}{y^4}}}\) và \(\frac{4}{{5{x^4}{y^3}}}\) là
\(10{x^4}{y^4}\).
\(10{x^4}{y^3}\).
\(10{x^3}{y^3}\).
\({x^4}{y^4}\).
Đáp án : A
+ Phân tích mẫu thức của mỗi phân thức đã cho thành nhân tử
+ Mẫu thức chung cần tìm là một tích mà các nhân tử được chọn như sau:
* Nhân tử bằng số của mẫu thức chung là tích các nhân tử bằng số của các mẫu dương ở Bước 1 (nếu các nhân tử bằng số của các mẫu thức là các số nguyên dương thì nhân tử bằng số của mẫu thức chung là BCNN của chúng);
* Với mỗi lũy thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn lũy thừa có số mũ cao nhất.
Mẫu thức chung của hai phân thức \(\frac{3}{{2{x^3}{y^4}}}\) và \(\frac{4}{{5{x^4}{y^3}}}\) là: \(10{x^4}{y^4}\).
Đáp án A
Kết quả rút gọn của biểu thức \(\frac{{{x^2} + 4x + 4}}{{9 - {{\left( {x + 5} \right)}^2}}}\) bằng
\(\frac{{x + 2}}{{8 - x}}\).
\(\frac{{ - x - 2}}{{x + 8}}\).
\(\frac{{x + 2}}{{x - 8}}\).
\(\frac{{x + 2}}{{x + 8}}\).
Đáp án : B
Phân tích tử thức, mẫu thức thành nhân tử sử dụng hằng đẳng thức sau đó chia cà tử và mẫu cho nhân tử chung.
Ta có:
\(\begin{array}{l}\frac{{{x^2} + 4x + 4}}{{9 - {{\left( {x + 5} \right)}^2}}} = \frac{{{{\left( {x + 2} \right)}^2}}}{{\left( {3 - x - 5} \right)\left( {3 + x + 5} \right)}}\\ = \frac{{{{\left( {x + 2} \right)}^2}}}{{\left( { - x - 2} \right)\left( {x + 8} \right)}} = \frac{{{{\left( {x + 2} \right)}^2}}}{{ - \left( {x + 2} \right)\left( {x + 8} \right)}} = \frac{{ - x - 2}}{{x + 8}}\end{array}\)
Đáp án B
Kết quả của phép tính \(\frac{{x{y^2}}}{{xy}} + \frac{{{x^2}y}}{{xy}}\) bằng
\({\left( {xy} \right)^2}\).
\(xy\).
\(2x{y^2}\).
\(x + y\).
Đáp án : D
Sử dụng quy tắc cộng hai phân thức cùng mẫu: \(\frac{A}{B} + \frac{C}{B} = \frac{{A + C}}{B}\).
Ta có:
\(\frac{{x{y^2}}}{{xy}} + \frac{{{x^2}y}}{{xy}} = \frac{{x{y^2} + {x^2}y}}{{xy}} = \frac{{xy\left( {y + x} \right)}}{{xy}} = x + y\).
Đáp án D
Phân thức \(K\left( x \right)\) thỏa mãn \(K\left( x \right):\frac{x}{{4 - x}} = \frac{{4 - x}}{2}\) là
\(\frac{{4 - x}}{{x - 2}}\).
\(\frac{2}{x}\).
\(\frac{x}{2}\).
\(\frac{{x - 2}}{4}\).
Đáp án : C
Chuyển vế để tìm K(x).
Ta có:
\(\begin{array}{l}K\left( x \right):\frac{x}{{4 - x}} = \frac{{4 - x}}{2}\\K\left( x \right) = \frac{{4 - x}}{2}.\frac{x}{{4 - x}}\\K\left( x \right) = \frac{{\left( {4 - x} \right).x}}{{2\left( {4 - x} \right)}}\\K\left( x \right) = \frac{x}{2}\end{array}\)
Đáp án C
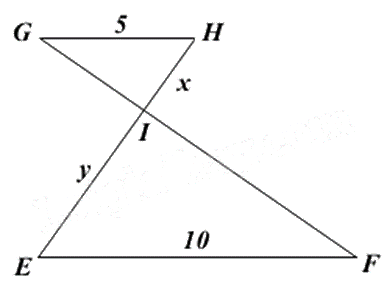
Cho $\Delta GHI\backsim \Delta FEI$ có các kính thước như hình vẽ, khi đó tỉ số độ dài của \(x\) và \(y\) bằng:
6.
2.
3.
\(\frac{1}{2}\).
Đáp án : D
Dựa vào hai tam giác đồng dạng suy ra tỉ lệ giữa các cạnh tương ứng của hai tam giác đó.
$\Delta GHI\backsim \Delta FEI$ nên \(\frac{{HI}}{{IE}} = \frac{{GH}}{{EF}}\)
Thay số: \(\frac{x}{y} = \frac{5}{{10}} = \frac{1}{2}\).
Đáp án D
Cho hình thang vuông ABCD (\(\widehat A = \widehat D = 90^\circ \)) có \(DB \bot BC\), AB = 4cm, CD = 9cm. Độ dài đoạn thẳng BD là:
6cm.
8cm.
9cm.
12cm.
Đáp án : A
Chứng minh $\Delta ABD\backsim \Delta BDC$ suy ra tỉ lệ giữa các cặp cạnh tương ứng, biến đổi để tính BD.
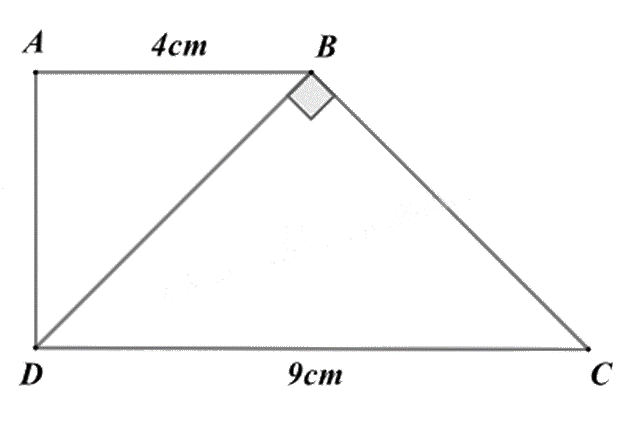
Xét \(\Delta ABD\) và \(\Delta BDC\) có:
\(\widehat {BAD} = \widehat {DBC}\left( { = 90^\circ } \right)\)
\(\widehat {ABD} = \widehat {BDC}\) (hai góc so le trong)
nên $\Delta ABD\backsim \Delta BDC$ (g.g)
suy ra \(\frac{{AB}}{{BD}} = \frac{{BD}}{{CD}}\), do đó \(B{D^2} = AB.CD = 4.9 = 36\)
suy ra \(BD = \sqrt {36} = 6\left( {cm} \right)\).
Đáp án A
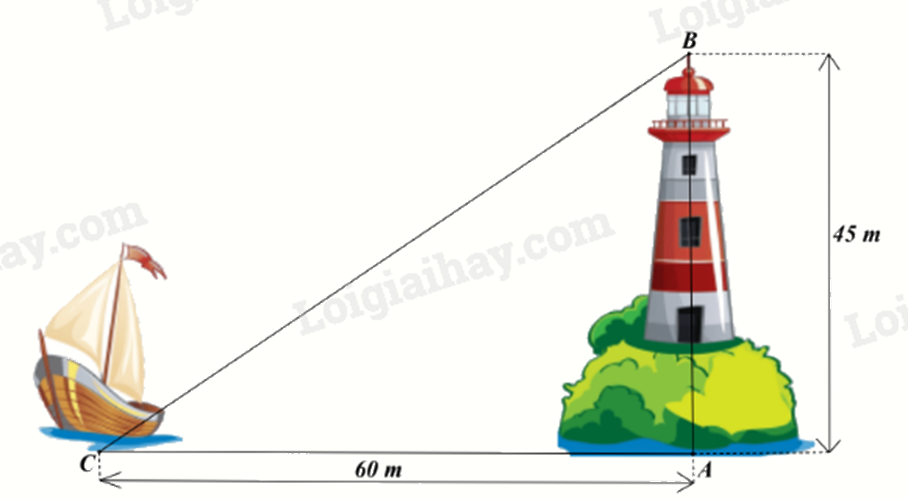
Ngọn hải đăng Lý Sơn (thuộc tỉnh Quảng Ngãi) cao 45m. Một con tàu đậu cách chân ngọn hải đăng 60m. Khoảng cách từ tàu đến đỉnh ngọn hải đăng là
75m.
105m.
85m.
55m.
Đáp án : A
Sử dụng định lí Pythagore vào tam giác ABC vuông tại A.
Khoảng cách từ tàu đến đỉnh ngọn hải đăng là độ dài đoạn BC trong hình vẽ.
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {45^2} + {60^2}\)
Suy ra \(BC = \sqrt {{{45}^2} + {{60}^2}} = 75\left( m \right)\)
Đáp án A
Cho tam giác \(ABC\), điểm \(M\) thuộc cạnh \(BC\) sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\). Đường thẳng đi qua \(M\) và song song với \(AC\) cắt \(AB\) ở \(D\). Đường thẳng đi qua \(M\) và song song với \(AB\) cắt \(AC\) ở \(E\). Tỉ số chu vi hai tam giác \(\Delta DBM\) và \(\Delta EMC\) là
\(\frac{2}{3}\).
\(\frac{1}{2}\).
\(\frac{1}{4}\).
\(\frac{1}{3}\).
Đáp án : B
Sử dụng định lí hai tam giác đồng dạng để chứng minh $\Delta BDM\backsim \Delta BAC,\Delta CEM\backsim \Delta CAB$, suy ra $\Delta BDM\backsim \Delta MEC$.
Tỉ số chu vi của hai tam giác đồng dạng bằng tỉ số các cạnh tương ứng của hai tam giác đồng dạng đó.
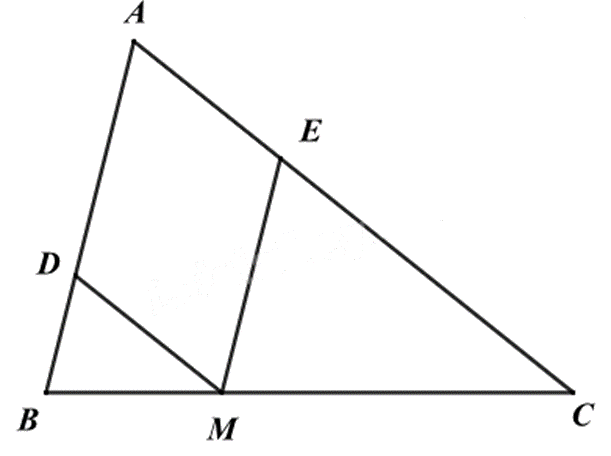
Vì DM // AC nên $\Delta BDM\backsim \Delta BAC$ (định lí hai tam giác đồng dạng)
Vì ME // AC nên $\Delta CEM\backsim \Delta CAB$ (định lí hai tam giác đồng dạng)
Suy ra $\Delta BDM\backsim \Delta MEC$.
Do đó \(\frac{{BD}}{{ME}} = \frac{{BM}}{{MC}} = \frac{{DM}}{{EC}} = \frac{1}{2}\).
Do đó \(\frac{{{C_{\Delta BDM}}}}{{{C_{\Delta MEC}}}} = \frac{1}{2}\).
Đáp án B
Cho \(\Delta ABC\) và \(\Delta MNP\) có: \(\widehat A = \widehat M = 90^\circ \). Để kết luận $\Delta ABC\backsim \Delta MNP$ theo trường hợp cạnh huyền – cạnh góc vuông thì cần có thêm điều kiện nào sau đây
\(\widehat B = \widehat N\).
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\).
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\).
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{MP}}\).
Đáp án : B
Trường hợp cạnh huyền – cạnh góc vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
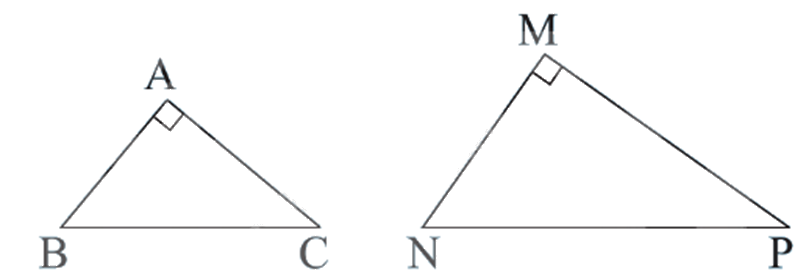
Để $\Delta ABC\backsim \Delta MNP\left( \widehat{A}=\widehat{M}=90{}^\circ \right)$ theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm điều kiện \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\) hoặc \(\frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\).
Vậy đáp án B đúng.
Đáp án B
Trong các hình sau hình nào có 2 hình đồng dạng

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đáp án : A
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’.
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H.
Cặp hình trong hình 1 là hai hình đồng dạng.
Đáp án A
Cho biểu thức \(A = \left( {\frac{{{x^2} + 1}}{{{x^2} + x}} + \frac{2}{{x + 1}}} \right):\frac{{{{\left( {x + 1} \right)}^2}}}{{2x}}\) với \(x \ne 0;{\mkern 1mu} {\mkern 1mu} x \ne - 1\).
a) Rút gọn biểu thức A ta được kết quả \(A = - \frac{2}{{x + 1}}\).
b) Khi \(x = - 1\) thì giá trị biểu thức là 2.
c) Biểu thức \(A = 1\) khi \(x = 1\).
d) Để \(A \in \mathbb{Z}\) thì \(x \in \left\{ { - 3; - 2;1;0} \right\}\).
a) Rút gọn biểu thức A ta được kết quả \(A = - \frac{2}{{x + 1}}\).
b) Khi \(x = - 1\) thì giá trị biểu thức là 2.
c) Biểu thức \(A = 1\) khi \(x = 1\).
d) Để \(A \in \mathbb{Z}\) thì \(x \in \left\{ { - 3; - 2;1;0} \right\}\).
a) Sử dụng các quy tắc tính toán với phân thức.
b) Kiểm tra xem \(x = - 1\) có thoả mãn điều kiện không, nếu có, thay \(x = - 1\) vào A.
c) Từ \(A = 1\) giải để tìm x.
d) Để A nguyên thì \(\frac{k}{{g\left( x \right)}}\) nguyên, hay \(k \vdots g\left( x \right)\).
Lập bảng để tìm các giá trị của x.
a) Sai
Ta có:
\(A = \left( {\frac{{{x^2} + 1}}{{{x^2} + x}} + \frac{2}{{x + 1}}} \right):\frac{{{{\left( {x + 1} \right)}^2}}}{{2x}}\) với \(x \ne 0;{\mkern 1mu} {\mkern 1mu} x \ne - 1\)
\(\begin{array}{l} = \left[ {\frac{{{x^2} + 1}}{{x\left( {x + 1} \right)}} + \frac{{2x}}{{x\left( {x + 1} \right)}}} \right].\frac{{2x}}{{{{\left( {x + 1} \right)}^2}}}\\ = \frac{{{x^2} + 2x + 1}}{{x\left( {x + 1} \right)}}.\frac{{2x}}{{{{\left( {x + 1} \right)}^2}}}\\ = \frac{{{{\left( {x + 1} \right)}^2}.2x}}{{x{{\left( {x + 1} \right)}^3}}}\\ = \frac{2}{{x + 1}}\end{array}\)
b) Sai
Vì \(x = - 1\) không thoả mãn điều kiện xác định nên ta không tính được giá trị của A.
c) Đúng
Ta có:
\(\begin{array}{l}A = 1\\\frac{2}{{x + 1}} = 1\\x + 1 = 2\\x = 2 - 1\\x = 1\end{array}\)
Vậy \(x = 1\) thì \(A = 1\).
d) Sai
Để \(A \in \mathbb{Z}\) thì \(\frac{2}{{x + 1}}\) nguyên, hay \(\left( {x + 1} \right) \in \) Ư\(\left( 2 \right) = \left\{ { - 2; - 1;1;2} \right\}\).
Ta có bảng giá trị sau:
Vậy \(x = \left\{ { - 3; - 2;1} \right\}\) thì A có giá trị nguyên.
Đáp án: SSĐS
Cho \(\Delta ABC\) có AB = 2cm, AC = 4cm. Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\). Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\).
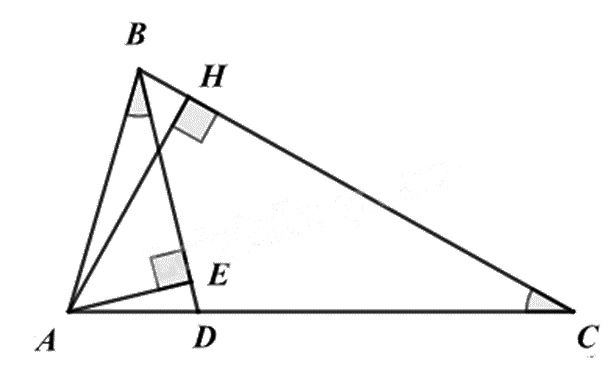
a) $\Delta ABD\backsim \Delta ACB$.
b) \(\widehat {ADB} = \widehat {ABC}\).
c) \(AD = 0,5cm,DC = 3,5cm\).
d) \({S_{\Delta ABH}} = 4{S_{\Delta ADE}}\).
a) $\Delta ABD\backsim \Delta ACB$.
b) \(\widehat {ADB} = \widehat {ABC}\).
c) \(AD = 0,5cm,DC = 3,5cm\).
d) \({S_{\Delta ABH}} = 4{S_{\Delta ADE}}\).
a) Sử dụng trường hợp đồng dạng góc – góc.
b) Từ hai tam giác đồng dạng suy ra các góc tương ứng bằng nhau.
c) Từ hai tam giác đồng dạng tỉ lệ giữa các cạnh tương ứng.
d) Chứng minh $\Delta ABH\backsim \Delta ADE$ suy ra tỉ số đồng dạng k của hai tam giác.
Tỉ số đồng dạng của diện tích hai tam giác bằng \({k^2}\).
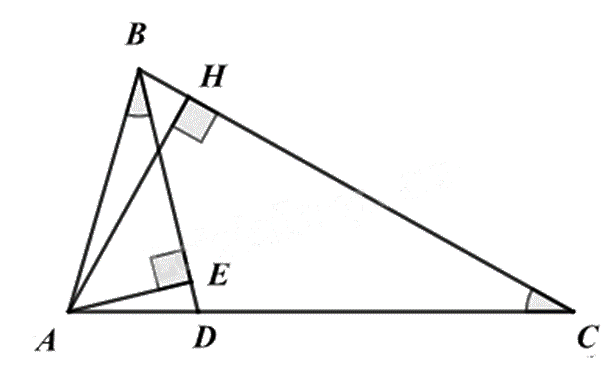
a) Đúng
Xét \(\Delta ABD\) và \(\Delta ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (chung)
\(\widehat A\) chung
suy ra $\Delta ABD\backsim \Delta ACB$ (g.g)
b) Đúng
Vì $\Delta ABD\backsim \Delta ACB$ (ý a) nên \(\widehat {ADB} = \widehat {ABC}\) (2 góc tương ứng)
c) Sai
Vì $\Delta ABD\backsim \Delta ACB$ nên \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\)
Thay số \(\frac{2}{4} = \frac{{AD}}{2}\), suy ra \(AD = \frac{{2.2}}{4} = 1\left( {cm} \right)\).
Do đó \(DC = AC - AD = 4 - 1 = 3\left( {cm} \right)\).
d) Đúng
Ta có: \(\widehat {ADB} = \widehat {ABC}\) (ý b), hay \(\widehat {ADE} = \widehat {ABH}\).
Xét \(\Delta ABH\) và \(\Delta ADE\) có:
\(\widehat {AHB} = \widehat {AED}\left( { = 90^\circ } \right)\)
\(\widehat {ADE} = \widehat {ABH}\) (cmt)
suy ra $\Delta ABH\backsim \Delta ADE$ (g.g)
Suy ra \(\frac{{AE}}{{AH}} = \frac{{DE}}{{BH}} = \frac{{AB}}{{AD}} = \frac{2}{1} = 2 = k\).
Do đó \(\frac{{{S_{\Delta ABH}}}}{{{S_{\Delta ADE}}}} = {k^2} = {2^2} = 4\). Suy ra \({S_{\Delta ABH}} = 4{S_{\Delta ADE}}\).
Đáp án: ĐĐSĐ
Cho phân thức \(H\left( x \right)\) thỏa mãn \(\frac{x}{{3 - x}} - H\left( x \right) = \frac{2}{{3 - x}}\). Giá trị của \(H\left( x \right)\) tại \(x = 2\) là.
Đáp án:
Đáp án:
Sử dụng quy tắc chuyển vế và trừ hai phân thức cùng mẫu để tính \(H\left( x \right)\).
Sau đó thay \(x = 2\) (kiểm tra điều kiện của \(H\left( x \right)\)) vào phân thức \(H\left( x \right)\).
Ta có:
\(\begin{array}{l}\frac{x}{{3 - x}} - H\left( x \right) = \frac{2}{{3 - x}}\\H\left( x \right) = \frac{x}{{3 - x}} - \frac{2}{{3 - x}}\\H\left( x \right) = \frac{{x - 2}}{{3 - x}}\end{array}\)
ĐKXĐ của \(H\left( x \right)\) là \(x \ne 3\).
Thay \(x = 2\) (TM) vào \(H\left( x \right)\), ta được:
\(H\left( 2 \right) = \frac{{2 - 2}}{{3 - 2}} = 0\).
Đáp án: 0
Biết cái cây có chiều cao \(CD = 5m\) và khoảng cách \(AC = 32m\), \(EC = 8m\). Chiều cao \(AB\) của ngôi nhà là …m.
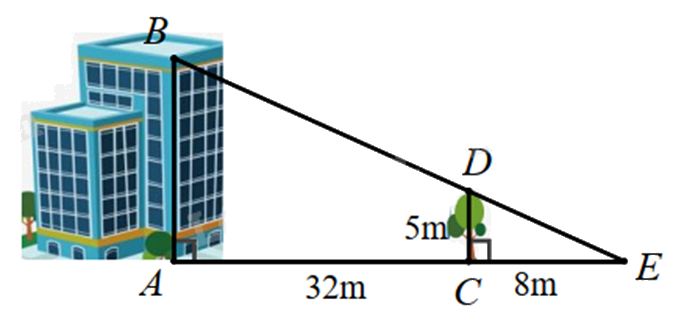
Đáp án:
Đáp án:
Từ đề bài xác định được độ dài các đoạn thẳng tương ứng.
Sử dụng định lí hai tam giác đồng dạng để chứng minh $\Delta CDE\backsim \Delta ABE$.
Từ đó biểu diễn tỉ lệ giữa các cạnh tương ứng để tính AB.
Vì cái cây và ngôi nhà cùng vuông góc với mặt đất nên chúng song song với nhau nên CD // AB.
Do đó $\Delta CDE\backsim \Delta ABE$ (định lí hai tam giác bằng nhau)
Suy ra \(\frac{{CE}}{{AE}} = \frac{{CD}}{{AB}}\) hay \(\frac{{CE}}{{AC + CE}} = \frac{{CD}}{{AB}}\)
Thay số: \(\frac{8}{{32 + 8}} = \frac{5}{{AB}}\), suy ra \(AB = 5:\frac{8}{{32 + 8}} = 25\left( m \right)\)
Vậy chiều cao \(AB\) của ngôi nhà là 25m.
Đáp án: 25
Một chiếc ti vi 24 inch có nghĩa là đường chéo màn hình của nó có độ dài là 24 inch (inch: đơn vị đo độ dài sử dụng ở nước Anh và một số nước khác, 1 inch \( \approx \) 2,54cm). Biết một ti vi màn hình phẳng có chiều dài, chiều rộng của màn hình lần lượt là 14,8 inch và 11,8 inch thì tivi đó thuộc loại bao nhiêu inch? (làm tròn đến chữ số thập phân thứ nhất)

Đáp án:
Đáp án:
Áp dụng định lí Pythagore vào tam giác vuông để tính được đường chéo của tam giác vuông.

Giả sử ta có tam giác ABC với chiều rộng AB = 11,8 inch, chiều dài AC = 14,8 inch.
Khi đó đường chéo của tam giác ABC là:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {11,{8^2} + 14,{8^2}} \approx 19\left( {inch} \right)\)
Vậy tivi đó thuộc loại 19 inch.
Đáp án: 19
Tổng các giá trị của y để biểu thức \(\frac{{1 + {y^2} + \frac{1}{y}}}{{2 + \frac{1}{y}}}\) bằng 1 là
Đáp án:
Đáp án:
Viết biểu thức bằng 1 rồi giải để tìm các giá trị y thoả mãn.
\(\frac{{1 + {y^2} + \frac{1}{y}}}{{2 + \frac{1}{y}}}\) (ĐKXĐ:\(y \ne 0\), \(y \ne - \frac{1}{2}\))
Ta có: \(\frac{{1 + {y^2} + \frac{1}{y}}}{{2 + \frac{1}{y}}} = 1\)
\(\begin{array}{l}1 + {y^2} + \frac{1}{y} = 2 + \frac{1}{y}\\1 + {y^2} + \frac{1}{y} - 2 - \frac{1}{y} = 0\\{y^2} - 1 = 0\\{y^2} = 1\\y = \pm 1\end{array}\)
Vậy tổng các giá trị của y để biểu thức \(\frac{{1 + {y^2} + \frac{1}{y}}}{{2 + \frac{1}{y}}}\) bằng 1 là: \( - 1 + 1 = 0\)
Đáp án: 0
a) Thực hiện phép tính: \(\frac{1}{{2\left( {x + 3} \right)}} + \frac{3}{{2x\left( {x + 3} \right)}}\).
b) Tìm đa thức A thỏa mãn \(\frac{A}{{x - 2}} = \frac{{2{x^3} + 4{x^2}}}{{{x^2} - 4}}\), \(x \ne \pm 2\).
a) Sử dụng quy tắc cộng hai phân thức khác mẫu:
- Quy đồng mẫu thức
- Cộng các tử thức với nhau và giữ nguyên mẫu thức
- Rút gọn phân thức (nếu cần).
b) Rút gọn biểu thức ở vế trái, khi đó ta sẽ tìm được đa thức A.
a) Ta có:
\(\begin{array}{l}\frac{1}{{2\left( {x + 3} \right)}} + \frac{3}{{2x\left( {x + 3} \right)}}\\ = \frac{x}{{2x\left( {x + 3} \right)}} + \frac{3}{{2x\left( {x + 3} \right)}}\\ = \frac{{x + 3}}{{2x\left( {x + 3} \right)}}\\ = \frac{1}{{2x}}\end{array}\)
b) Ta có:
\(\frac{A}{{x - 2}} = \frac{{2{x^3} + 4{x^2}}}{{{x^2} - 4}}\)
\(\begin{array}{l}\frac{A}{{x - 2}} = \frac{{2{x^2}\left( {x + 2} \right)}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}\\\frac{A}{{x - 2}} = \frac{{2{x^2}}}{{x - 2}}\end{array}\)
suy ra \(A = 2{x^2}\).
Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh $\Delta ABC\backsim \Delta HBA$.
b) Tia phân giác của góc AHC cắt AC tại D. Chứng minh \(\frac{{HB}}{{HC}} = \frac{{A{D^2}}}{{D{C^2}}}\).
a) Chứng minh $\Delta ABC\backsim \Delta HBA$ theo trường hợp góc – góc.
b) Chứng minh $\Delta AHC\backsim \Delta BHA\left( g.g \right)$, suy ra tỉ lệ giữa các cạnh tương ứng, từ đó ta có: \(A{H^2} = HB.HC\)
Nhân cả hai vế với HC và biểu diễn tỉ lệ thức tạo thành: \(\frac{{HB}}{{HC}} = \frac{{A{H^2}}}{{H{C^2}}}\).
Sử dụng tính chất của đường phân giác trong tam giác, ta có: \(\frac{{AH}}{{HC}} = \frac{{AD}}{{DC}}\) (HD là đường phân giác của tam giác AHC)
Kết hợp ta được điều phải chứng minh.
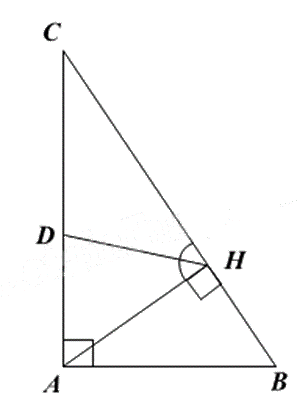
a) Xét \(\Delta ABC\) và \(\Delta HBA\), ta có:
\(\begin{array}{l}\widehat A = \widehat H\left( { = 90^\circ } \right)\\\widehat B\,{\rm{chung}}\end{array}\)
Suy ra $\Delta ABC\backsim \Delta HBA\left( g.g \right)$.
c) Xét \(\Delta AHC\) và \(\Delta BHA\) có:
\(\widehat {AHC} = \widehat {BHA}\left( { = 90^\circ } \right)\)
\(\widehat {CAH} = \widehat {ABH}\) (cùng phụ với \(\widehat C\))
Suy ra $\Delta AHC\backsim \Delta BHA\left( g.g \right)$
Do đó \(\frac{{AH}}{{HC}} = \frac{{HB}}{{AH}}\)
suy ra \(A{H^2} = HB.HC\)
Nhân cả hai vế với HC, ta được:
\(A{H^2}.HC = HB.H{C^2}\)
Do đó \(\frac{{HB}}{{HC}} = \frac{{A{H^2}}}{{H{C^2}}}\)
Mà HD là đường phân giác của tam giác AHC nên \(\frac{{AH}}{{HC}} = \frac{{AD}}{{DC}}\)
Do đó \(\frac{{HB}}{{HC}} = \frac{{A{D^2}}}{{D{C^2}}}\) (đpcm).
Một người tiến hành đo khoảng cách từ điểm A bên này sông đến điểm B bên kia sông như hình vẽ sau. Người đó vạch trên bờ sông một đường thẳng d đi qua A và vuông góc với đường thẳng AB, sau đó xác định hai điểm C và D sao cho \(\widehat {ACB} = 50^\circ \) và \(\widehat {ADC} = 40^\circ \). Người đó đo được \(AC = 12,25m;AD = 16m\). Tính khoảng cách AB.
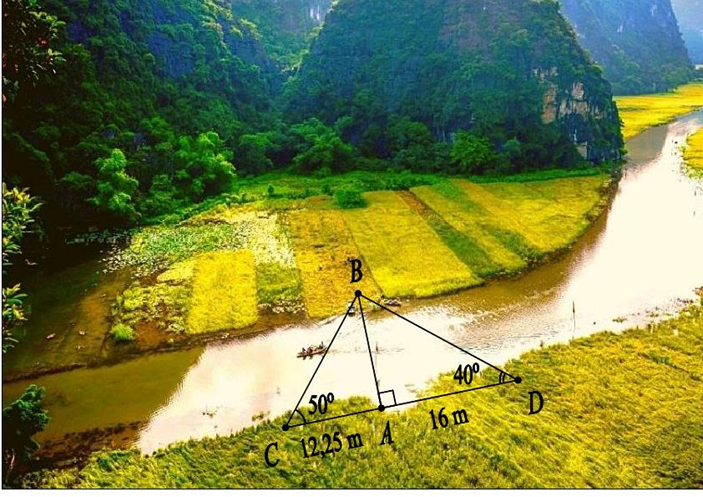
Sử dụng định lí tổng 3 góc trong một tam giác bằng \(180^\circ \) suy ra \(\widehat B = 90^\circ \).
Chứng minh $\Delta ABC\backsim \Delta ADB\left( g.g \right)$, suy ra tỉ lệ đồng dạng giữa các cạnh tương ứng, từ đó tính AB.
Xét tam giác ABC có \(\widehat B = 180^\circ - \left( {\widehat C + \widehat D} \right) = 180^\circ - \left( {50^\circ + 40^\circ } \right) = 90^\circ \)
Xét \(\Delta ABC\) và \(\Delta ADB\) có:
\(\widehat {CAB} = \widehat {BAD}\left( { = 90^\circ } \right)\)
\(\widehat C = \widehat {ABD}\) (cùng phụ với \(\widehat D\))
nên $\Delta ABC\backsim \Delta ADB\left( g.g \right)$
suy ra \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
Do đó \(A{B^2} = AD.AC\)
Suy ra \(AB = \sqrt {AD.AC} = \sqrt {16.12,25} = 14\)
Vậy khoảng cách AB là 14m.
Đề thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 10 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một nửa học kì. Đề thi này không chỉ kiểm tra kiến thức đã học mà còn rèn luyện kỹ năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết để giúp học sinh ôn tập hiệu quả.
Thông thường, đề thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 10 có cấu trúc bao gồm hai phần chính:
Dưới đây là một số dạng bài tập thường gặp trong đề thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 10:
Để giúp học sinh làm quen với các dạng bài tập thường gặp, chúng ta sẽ cùng nhau giải chi tiết một số bài tập mẫu:
Lời giải:
Vậy nghiệm của phương trình là x = 2.
Lời giải:
Áp dụng định lý Pitago vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42 = 9 + 16 = 25
BC = √25 = 5cm
Vậy độ dài cạnh BC là 5cm.
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 10!