Chào mừng các em học sinh lớp 8 đến với đề thi học kì 1 môn Toán - Đề số 4, chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 1.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Kết quả thương của phép chia \(\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\) là:
Giá trị của đa thức \({x^3}y - 14{y^3} - 6x{y^2} + y + 2\) tại x = -1 ; y = 0,5 là:
Ghép mỗi ý ở cộtA với mỗi ý ở cột B để được kết quả đúng.
a. \(\left( {x - y} \right)\left( {x + y} \right)\)
b. \(10x - 25 - {x^2}\)
c. \(8{x^3} - \frac{1}{8}\)
1. \( - {\left( {x - 5} \right)^2}\)
2. \({x^2} - {y^2}\)
3. \(\left( {2x - \frac{1}{2}} \right)\left( {4{x^2} + x + \frac{1}{4}} \right)\)
Hai đường chéo của hình chữ nhật
Một tứ giác là hình bình hành nếu nó là:
Những tứ giác nào sau đây có hai đường chéo bằng nhau?
Cho tam giác ABC có AB = 9cm; \(D \in AB\) sao cho AD = 6cm. Kẻ DE // BC (\(E \in AC\)); EF // CD (\(F \in AB\)). Tính độ dài AF.
Cho tam giác ABC có ba đường trung tuyến AI, BD, CE đồng quy tại G. Gọi M và N lần lượt là trung điểm của GC và GB. Khi đó, tứ giác MNED là hình gì?
Cho tam giác ABC, AC = 2AB, AD là tia phân giác của tam giác ABC, khi đó \(\frac{{BD}}{{CD}} =?\)
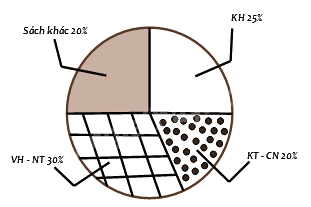
Bạn Châu vẽ biểu đồ hình quạt tròn như hình bên để biểu diễn tỉ lệ các loại sách trong thư viện: Khoa học (KH), Kĩ thuật và công nghệ (KT & CN), Văn học và Nghệ thuật (VH – NT); Sách khác. Những dữ liệu mà bạn Châu nêu ra trong biểu đồ hình quạt tròn dữ liệu nào chưa hợp lí?
Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2020.
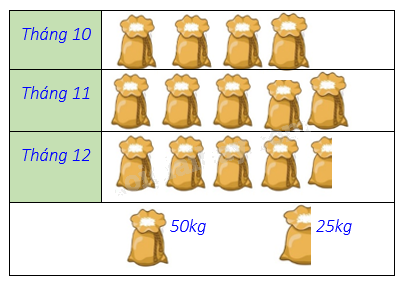
Nêu số kg gạo bán được ở tháng 12?
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ tranh ở hình bên?
So tháng 10 số gạo bán được của tháng 11 tăng bao nhiêu phần trăm?
Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến.
a) \(A = 2xy + \frac{1}{2}x.\left( {2x - 4y + 4} \right) - x\left( {x + 2} \right)\)
b) \(B = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\)
Tìm x biết
a) \(9{x^2} - 72x = 0\)
b) \(\left( {16 - 4x} \right)\left( {x + 3} \right) - \left( {x + 1} \right)\left( {4 - 4x} \right) = 0\)
Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022.
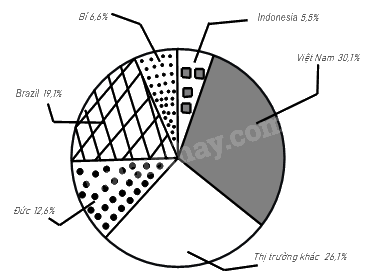
(Nguồn: Eurostat)
a) Trong 7 tháng đầu năm 2022 thị trường nào cung cấp cà phê cho Tây Ban Nha là nhiều nhất, ít nhất?
b) Biết lượng cà phê mà tất cả các thị trường cung cấp cho Tây Ban Nha trong 7 tháng đầu năm 2022 là 222 956 tấn. Lập bảng thống kê lượng cà phê mà các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022 theo mẫu sau:
Thị trường | Đức | Brazil | Bỉ | Indonesia | Việt Nam | Khác |
Lượng cà phê (tấn) | ? | ? | ? | ? | ? | ? |
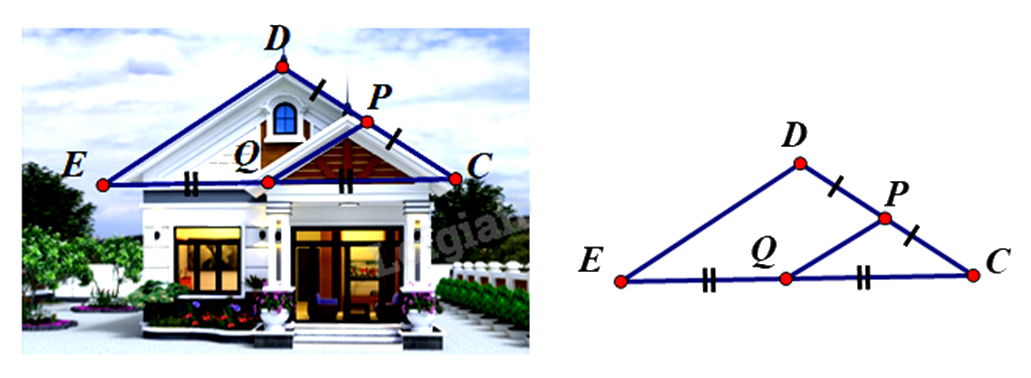
1. Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Em hãy tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?
2. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Gọi M và N theo thứ tự là trung điểm của các đoạn AH và DH.
a) Chứng minh MN//AD.
b) Gọi I là trung điểm của cạnh BC. Chứng minh tứ giác BMNI là hình bình hành.
c) Chứng minh tam giác ANI vuông tại N.
Tìm giá trị nhỏ nhất của biểu thức:\(A = 4{x^2} - 12x + 15\).
Kết quả thương của phép chia \(\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\) là:
Đáp án : C
Sử dụng quy tắc chia đa thức cho đơn thức.
Ta có:
\(\begin{array}{l}\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\\ = 3x{y^2}:\left( { - \frac{1}{2}x} \right) - 2{x^2}y:\left( { - \frac{1}{2}x} \right) + {x^3}:\left( { - \frac{1}{2}x} \right)\\ = - 6{y^2} + 4xy - 2{x^2}\end{array}\)
Giá trị của đa thức \({x^3}y - 14{y^3} - 6x{y^2} + y + 2\) tại x = -1 ; y = 0,5 là:
Đáp án : D
Thay x = -1 ; y = 0,5 vào biểu thức để tính giá trị.
Thay x = -1 ; y = 0,5 vào biểu thức, ta được:
\(\begin{array}{l}{( - 1)^3}.0,5 - 14{(0,5)^3} - 6( - 1){(0,5)^2} + 0,5 + 2\\ = - 0,5 - 14.0,125 + 6.0,25 + 0,5 + 2\\ = - 0,5 - 1,75 + 1,5 + 0,5 + 2\\ = 1,75\end{array}\)
Ghép mỗi ý ở cộtA với mỗi ý ở cột B để được kết quả đúng.
a. \(\left( {x - y} \right)\left( {x + y} \right)\)
b. \(10x - 25 - {x^2}\)
c. \(8{x^3} - \frac{1}{8}\)
1. \( - {\left( {x - 5} \right)^2}\)
2. \({x^2} - {y^2}\)
3. \(\left( {2x - \frac{1}{2}} \right)\left( {4{x^2} + x + \frac{1}{4}} \right)\)
a. \(\left( {x - y} \right)\left( {x + y} \right)\)
2. \({x^2} - {y^2}\)
b. \(10x - 25 - {x^2}\)
1. \( - {\left( {x - 5} \right)^2}\)
c. \(8{x^3} - \frac{1}{8}\)
3. \(\left( {2x - \frac{1}{2}} \right)\left( {4{x^2} + x + \frac{1}{4}} \right)\)
Sử dụng kiến thức về các hằng đẳng thức đáng nhớ.
a. \(\left( {x - y} \right)\left( {x + y} \right) = {x^2} - {y^2} \Rightarrow \) a – 2.
b. \(10x - 25 - {x^2} = - {x^2} + 10x - 25 = - \left( {{x^2} - 10x + 25} \right) = - {\left( {x - 5} \right)^2} \Rightarrow \) b – 1.
c. \(8{x^3} - \frac{1}{8} = \left( {2x - \frac{1}{2}} \right)\left( {4{x^2} + x + \frac{1}{4}} \right) \Rightarrow \) c – 3.
Đáp án: a – 2; b – 1; c – 3.
Hai đường chéo của hình chữ nhật
Đáp án : C
Sử dụng tính chất của hình chữ nhật.
Hai đường chéo của hình chữ nhật bằng nhau nên chọn đáp án C.
Một tứ giác là hình bình hành nếu nó là:
Đáp án : C
Dựa vào kiến thức về hình bình hành.
Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên chọn đáp án C.
Những tứ giác nào sau đây có hai đường chéo bằng nhau?
Đáp án : B
Dựa vào kiến thức về các hình đã học.
Những tứ giác có hai đường chéo bằng nhau là: hình thang cân, hình chữ nhật, hình vuông nên chọn đáp án B.
Cho tam giác ABC có AB = 9cm; \(D \in AB\) sao cho AD = 6cm. Kẻ DE // BC (\(E \in AC\)); EF // CD (\(F \in AB\)). Tính độ dài AF.
Đáp án : C
Sử dụng định lí Thales để chứng minh.
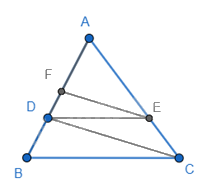
Ta có: DE // BC nên \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{6}{9} = \frac{2}{3}\) (định lí Thales)
EF // CD nên \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}} = \frac{2}{3}\) (định lí Thales)
\( \Rightarrow AF = \frac{2}{3}AD = \frac{2}{3}.6 = 4(cm)\).
Cho tam giác ABC có ba đường trung tuyến AI, BD, CE đồng quy tại G. Gọi M và N lần lượt là trung điểm của GC và GB. Khi đó, tứ giác MNED là hình gì?
Đáp án : B
Sử dụng tính chất đường trung bình.
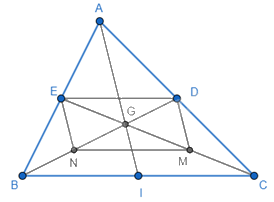
Ta có BD và CE là đường trung tuyến của tam giác ABC nên D là trung điểm của AC; E là trung điểm của AB, khi đó DE là đường trung bình của tam giác ABC nên DE // BC và DE = \(\frac{1}{2}\)BC. (1)
M và N lần lượt là trung điểm của GC và GB nên MN là đường trung bình của tam giác GBC nên MN // BC và MN = \(\frac{1}{2}\)BC. (2)
Từ (1) và (2) suy ra DE // MN và DE = MN => MNED là hình bình hành (hai cạnh đối song song và bằng nhau).
Cho tam giác ABC, AC = 2AB, AD là tia phân giác của tam giác ABC, khi đó \(\frac{{BD}}{{CD}} =?\)
Đáp án : D
Sử dụng tính chất của đường phân giác trong tam giác.
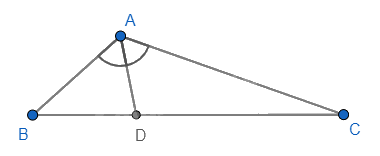
Ta có AD là tia phân giác của tam giác ABC nên \(\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = \frac{{AB}}{{2AB}} = \frac{1}{2}\) (tính chất của tia phân giác trong tam giác).
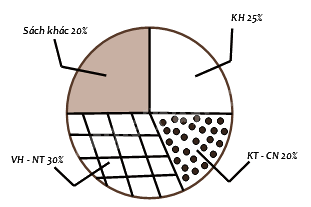
Bạn Châu vẽ biểu đồ hình quạt tròn như hình bên để biểu diễn tỉ lệ các loại sách trong thư viện: Khoa học (KH), Kĩ thuật và công nghệ (KT & CN), Văn học và Nghệ thuật (VH – NT); Sách khác. Những dữ liệu mà bạn Châu nêu ra trong biểu đồ hình quạt tròn dữ liệu nào chưa hợp lí?
Đáp án : A
Quan sát biểu đồ để chỉ ra dữ liệu chưa hợp lí.
Trong biểu đồ trên, ta thấy tỉ lệ của sách khác (20%) bằng tỉ lệ sách KT – CN (20%) nhưng phần biểu diễn của sách khác lại bằng với phần biểu diễn của sách KN (25%). nên dữ liệu sách khác, sách KT – CN hoặc sách KH chưa hợp lý.
Vì tổng tỉ lệ các loại sách là 100%, mà tổng số phần trăm trong biểu đồ trên là 30% + 20% + 25% + 20% = 95% < 100%.
Vậy ta suy ra dữ liệu chưa hợp lí là dữ liệu sách khác. Tỉ lệ của sách khác phải là 25% bằng với tỉ lệ của sách KH.
Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2020.
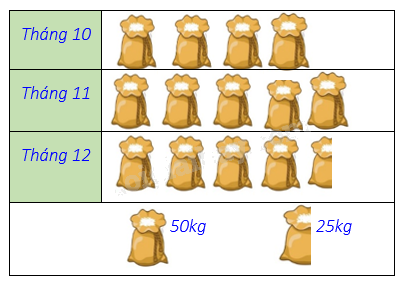
Nêu số kg gạo bán được ở tháng 12?
Đáp án: C
Quan sát biểu đồ tranh để trả lời câu hỏi.
Số kg gạo bán được ở tháng 12 là: 50.4 + 25 = 225 (kg).
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ tranh ở hình bên?
Đáp án: C
Quan sát biểu đồ tranh để trả lời câu hỏi.
Với dự liệu trong biểu đồ tranh trên, ta có thể biểu diễn các dữ liệu thống kê bằng biểu đồ cột.
So tháng 10 số gạo bán được của tháng 11 tăng bao nhiêu phần trăm?
Đáp án: A
Quan sát biểu đồ tranh để trả lời câu hỏi.
Số gạo tháng 10 bán được là: 50.4 = 200 (kg).
Số gạo tháng 11 bán được là: 50.5 = 250 (kg).
So với tháng 10, số gạo bán được của tháng 11 tăng là: 250 – 200 = 50 (kg).
Số gạo bán được của tháng 11 tăng so với tháng 10 số phần trăm là: \(\frac{{50}}{{200}}.100 = 25(\% )\)
Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến.
a) \(A = 2xy + \frac{1}{2}x.\left( {2x - 4y + 4} \right) - x\left( {x + 2} \right)\)
b) \(B = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\)
Sử dụng các phép tính với đa thức để rút gọn biểu thức.
a) \(A = 2xy + \frac{1}{2}x.\left( {2x - 4y + 4} \right) - x\left( {x + 2} \right)\)
\(\begin{array}{l} = 2xy + {x^2} - 2xy + 2x - {x^2} - 2x\\ = 0\end{array}\)
Vì A = 0 nên biểu thức A không phụ thuộc vào giá trị của biến.
b) \(B = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\)
\(\begin{array}{l} = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\\ = \left( {x + 2 - x + 3} \right)\left( {x + 2 + x - 3} \right) - 10x\\ = 5\left( {2x - 1} \right) - 10x\\ = 10x - 5 - 10x\\ = - 5\end{array}\)
Vì B = -5 nên biểu thức B không phụ thuộc vào giá trị của biến.
Tìm x biết
a) \(9{x^2} - 72x = 0\)
b) \(\left( {16 - 4x} \right)\left( {x + 3} \right) - \left( {x + 1} \right)\left( {4 - 4x} \right) = 0\)
Nhóm nhân tử chung để tìm x.
a) \(9{x^2} - 72x = 0\)
\(9x\left( {x - 8} \right) = 0\)
\(x = 0\) hoặc \(x - 8 = 0\)
\(x = 0\) hoặc \(x = 8\)
Vậy x = 0 hoặc x = 8.
b) \(\left( {16 - 4x} \right)\left( {x + 3} \right) - \left( {x + 1} \right)\left( {4 - 4x} \right) = 0\)
\(\begin{array}{l}4\left( {4 - x} \right)\left( {x + 3} \right) - 4\left( {x + 1} \right)\left( {1 - x} \right) = 0\\(4 - x)(x + 3) - (1 - {x^2}) = 0\\4x - {x^2} + 12 - 3x - 1 + {x^2} = 0\\x + 11 = 0\\x = - 11\end{array}\)
Vậy x = -11.
Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022.
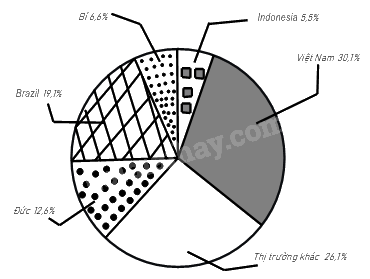
(Nguồn: Eurostat)
a) Trong 7 tháng đầu năm 2022 thị trường nào cung cấp cà phê cho Tây Ban Nha là nhiều nhất, ít nhất?
b) Biết lượng cà phê mà tất cả các thị trường cung cấp cho Tây Ban Nha trong 7 tháng đầu năm 2022 là 222 956 tấn. Lập bảng thống kê lượng cà phê mà các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022 theo mẫu sau:
Thị trường | Đức | Brazil | Bỉ | Indonesia | Việt Nam | Khác |
Lượng cà phê (tấn) | ? | ? | ? | ? | ? | ? |
Dựa vào biểu đồ để trả lời câu hỏi.
a) Trong 7 tháng đầu năm 2022, thị trường cung cấp cà phê cho Tây Ban Nha nhiều nhất là Việt Nam với 30,1%; thị trường cung cấp ít nhất là Indonesia với 5,5%.
b) Lượng cà phê Đức cung cấp cho Tây Ban Nha là: 222 956.12,6% = 28 092,456 (tấn)
Lượng cà phê Brazil cung cấp cho Tây Ban Nha là: 222 956.19,1% = 42 584,596 (tấn)
Lượng cà phê Bỉ cung cấp cho Tây Ban Nha là: 222 956.6,6% = 14 715,096 (tấn)
Lượng cà phê Indonesia cung cấp cho Tây Ban Nha là: 222 956.5,5% = 12 262,58 (tấn)
Lượng cà phê Việt Nam cung cấp cho Tây Ban Nha là: 222 956.30,1% = 67 109,756 (tấn)
Lượng cà phê thị trường khác cung cấp cho Tây Ban Nha là: 222 956.26,1% = 58 191,516 (tấn)
Ta có bảng giá trị:
Thị trường | Đức | Brazil | Bỉ | Indonesia | Việt Nam | Khác |
Lượng cà phê (tấn) | 28092,456 | 42584,596 | 14715,096 | 12262,58 | 67109,756 | 58191,516 |
1. Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Em hãy tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?
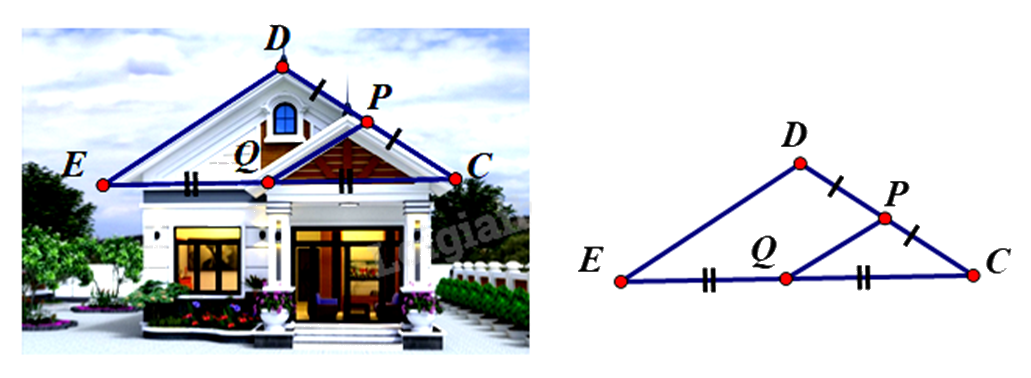
2. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Gọi M và N theo thứ tự là trung điểm của các đoạn AH và DH.
a) Chứng minh MN//AD.
b) Gọi I là trung điểm của cạnh BC. Chứng minh tứ giác BMNI là hình bình hành.
c) Chứng minh tam giác ANI vuông tại N.
1. Dựa vào tính chất của đường trung bình để tính.
2.
a) Dựa vào tính chất của đường trung bình để chứng minh.
b) Chứng mình BMNI có hai cạnh đối song song và bằng nhau.
c) Chứng minh M là trực tâm của tam giác ABN nên BM \( \bot \) AN, mà BM // NI nên AN \( \bot \) NI hay \(\widehat {ANI} = {90^0}\)=> ANI là tam giác vuông tại N.
1.
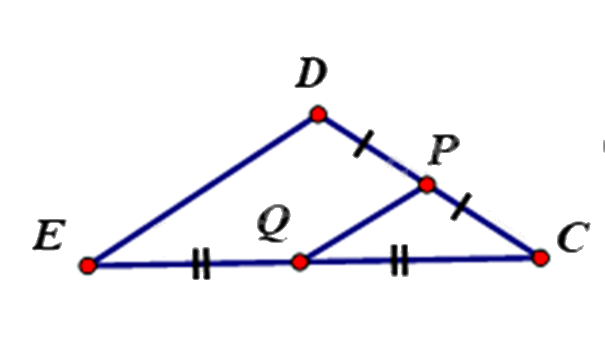
Vì Q là trung điểm EC, P là trung điểm của DC nên PQ là đường trung bình của tam giác CDE.
\(\begin{array}{l} \Rightarrow QP = \frac{1}{2}DE\\ \Rightarrow DE = 2QP = 2.1,5 = 3m\end{array}\)
Vậy chiều dài mái DE bằng 3m.
2.
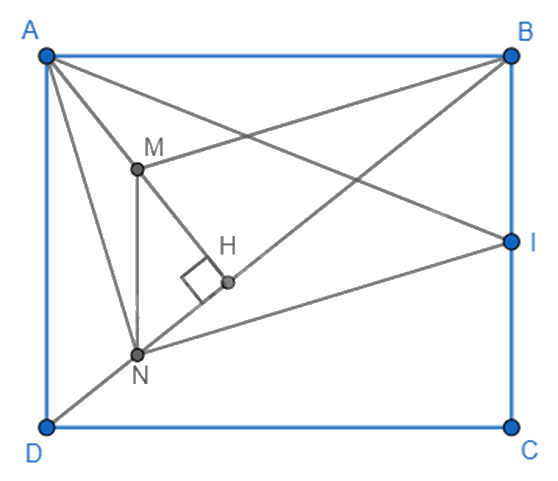
a) Ta có M là trung điểm của AH, N là trung điểm của DH nên MN là đường trung bình của tam giác ADH => MN // AD và MN = \(\frac{1}{2}\)
b) Vì ABCD là hình chữ nhật nên AD // BC và AD = BC; I là trung điểm của BC nên BI = \(\frac{1}{2}\)
=> MN // BI (cùng song song với AD) và MN = BI (= \(\frac{1}{2}\)BC = \(\frac{1}{2}\)AD). Khi đó BMNI là hình bình hành.
c) Ta có MN // AD mà AD \( \bot \) AB (ABCD là hình chữ nhật) nên MN \( \bot \) Xét tam giác ABN có AH \( \bot \) BN; MN \( \bot \) AB; AH giao MN tại N nên N là trực tâm của tam giác ABN. Suy ra BM \( \bot \) AN.
Mà BM // IN (BMNI là hình bình hành) nên AN \( \bot \) IN hay \(\widehat {ANI} = {90^0}\)=> ANI là tam giác vuông tại N.
Tìm giá trị nhỏ nhất của biểu thức:\(A = 4{x^2} - 12x + 15\).
Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức.
Ta có: \(4{x^2} - 12x + 15 = \left( {4{x^2} - 2.2x.3 + 9} \right) + 6 = {\left( {2x - 3} \right)^2} + 6\).
Vì \({\left( {2x - 3} \right)^2} \ge 0,\forall x \in \mathbb{R}\) nên \({\left( {2x - 3} \right)^2} + 6 \ge 6,\forall x \in \mathbb{R}\). Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức A.
\(\min A = 6 \Leftrightarrow 2x - 3 = 0 \Leftrightarrow x = \frac{3}{2}\).
Vậy giá trị nhỏ nhất của biểu thức A là 6 khi \(x = \frac{3}{2}\).
Đề thi học kì 1 Toán 8 - Đề số 4 chương trình Kết nối tri thức là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức, và các ứng dụng thực tế của toán học.
Thông thường, đề thi học kì 1 Toán 8 - Đề số 4 - Kết nối tri thức sẽ có cấu trúc gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi học kì 1 Toán 8 - Đề số 4 - Kết nối tri thức:
Để đạt kết quả tốt trong kỳ thi học kì 1 Toán 8, học sinh cần:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu ôn thi học kì 1 Toán 8 - Kết nối tri thức, bao gồm:
Trong quá trình làm bài thi, học sinh nên:
Đề thi học kì 1 Toán 8 - Đề số 4 - Kết nối tri thức là một cơ hội để học sinh thể hiện những kiến thức và kỹ năng đã học trong học kì. Với sự chuẩn bị kỹ lưỡng và tinh thần tự tin, các em sẽ đạt được kết quả tốt nhất. Chúc các em thành công!