Chào mừng các em học sinh lớp 8 đến với đề thi giữa kì 2 Toán 8 - Đề số 8 chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 2, chuẩn bị tốt nhất cho kỳ thi sắp tới.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán!
Một tàu du lịch đi từ Hải Phòng đến Quảng Ninh với quang đường dài \(50{\rm{\;km}}/{\rm{h}}\). Vận tốc của dòng nước là \(3{\rm{\;km}}/{\rm{h}}\). Gọi vận tốc thực của tàu là \(x{\rm{\;km}}/{\rm{h}}\). Hãy biểu diễn thời gian tàu đi ngược dòng từ Quảng Ninh tới Hải Phòng.
Quan sát hình sau và chỉ ra một cặp tam giác đồng dạng:
Đáp án nào dưới đây không là phương trình bậc nhất một ẩn?
Điều kiện xác định của phân thức \(\frac{{\left( {x - 1} \right)\left( {x + 3} \right)}}{{{x^2} - 1}}\) là:
Chọn khẳng định sai.
Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
Kết quả của phép chia \(\frac{{a - 2b}}{{16}}:\frac{{2a - 4b}}{{12}}\) bằng:
Nếu 2 tam giác \({\rm{ABC}}\) và \({\rm{DEF}}\) có \(\widehat A = \widehat D,\widehat C = \widehat F\) thì:
Tổng các nghiệm của hai phương trình \( - 6\left( {1,5 - 2x} \right) = 3\left( { - 15 + 2x} \right);5x + 10 = 0\) bằng:
Cho biết một nửa đàn bò đang gặm cỏ trên cánh đồng, \(\frac{1}{3}\) đàn bò đang nằm nghỉ gần đó, còn lại 4 con đang uống nước ở ao. Tính số bò hiện có trong đàn.
Cho biểu thức: \(B = \frac{1}{{x + 1}} - \frac{{{x^3} - x}}{{{x^2} + 1}} \cdot \left( {\frac{1}{{{x^2} + 2x + 1}} - \frac{1}{{{x^2} - 1}}} \right)\) (ĐKXĐ: \(\left. {x \ne \pm 1} \right)\)
a) Rút gọn \(B\)
b) Tính giá trị của \(B\) tại \(x = - 2\)
c) Với giá trị nào của \(x\) thì \(B = 1\)
Giải các phương trình sau:a) \(\frac{{9x + 5}}{6} = 1 - \frac{{6 + 3x}}{8}\);b) \(\frac{{x + 1}}{4} = \frac{1}{2} + \frac{{2x + 1}}{5}\);c) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{3}{2} - \frac{{1 - 2x}}{4}\).
Tổng số học sinh khối 8 và khối 9 của một trường là 580 em, trong đó có \(256\) em là học sinh giỏi. Tính số học sinh của mỗi khối, biết rằng số học sinh giỏi khối 8 chiếm tỉ lệ \(40{\rm{\% }}\) số học sinh khối 8, số học sinh giỏi khối 9 chiếm tỉ lệ 48% số học sinh khối 9.
Cho \(\Delta ABC\) có các đường cao \({\rm{BD}}\) và \({\rm{CE}}\) cắt nhau tại \({\rm{H}}\). Chứng minh:a) \(\Delta HBE\) đồng dạng với \(\Delta HCD\).b) \(\widehat {HDE} = \widehat {HAE}\).
Cho \(\frac{a}{{b + c}} + \frac{b}{{c + a}} + \frac{c}{{a + b}} = 1\). Chứng minh \(\frac{{{a^2}}}{{b + c}} + \frac{{{b^2}}}{{c + a}} + \frac{{{c^2}}}{{a + b}} = 0\)
Một tàu du lịch đi từ Hải Phòng đến Quảng Ninh với quang đường dài \(50{\rm{\;km}}/{\rm{h}}\). Vận tốc của dòng nước là \(3{\rm{\;km}}/{\rm{h}}\). Gọi vận tốc thực của tàu là \(x{\rm{\;km}}/{\rm{h}}\). Hãy biểu diễn thời gian tàu đi ngược dòng từ Quảng Ninh tới Hải Phòng.
Đáp án : A
Sử dụng công thức bài toán chuyển động dòng nước sau đó thiết lập biểu thức theo yêu cầu.
Vận tốc ngược dòng của tàu đi từ Quảng Ninh đến Hải Phòng là: \(x - 3\left( {{\rm{\;km}}/{\rm{h}}} \right)\)
Thời gian tàu đi ngược dòng từ Quảng Ninh đến Hải Phòng là: \(\frac{{50}}{{x - 3}}\) (giờ)
Đáp án A.
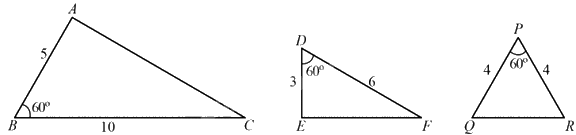
Quan sát hình sau và chỉ ra một cặp tam giác đồng dạng:
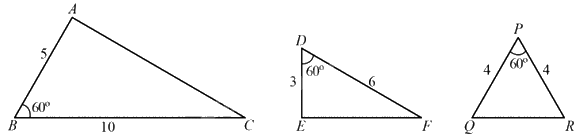
Đáp án : D
TH đồng dạng thứ hai (c-g-c): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
Xét \(\Delta ABC\) và \(\Delta EDF\) có: \(\left\{ {\begin{array}{*{20}{l}}{\widehat {ABC} = \widehat {EDF} = {{60}^0}}\\{\frac{{AB}}{{BC}} = \frac{{DE}}{{EF}} = \frac{1}{2}}\end{array}} \right.\) suy ra $\Delta ABC\backsim \Delta EDF$ (c.g.c)
Đáp án D.
Đáp án nào dưới đây không là phương trình bậc nhất một ẩn?
Đáp án : D
Phương trình dạng \({\rm{ax}} + {\rm{b}} = 0\), với \({\rm{a}}\) và \({\rm{b}}\) là hai số đã cho và \({\rm{a}} \ne 0\), được gọi là phương trình bậc nhất một ân.
Các phương trình \(3x + \frac{3}{5} = 0,\frac{2}{3}y - 7 = 0,7 = 2t\) có dạng nên là phương trình bậc nhất một ẩn.
Phương trình \({z^2} - 9 = 0\) có bậc hai nên không là phương trình bậc nhất một ẩn
Đáp án D.
Điều kiện xác định của phân thức \(\frac{{\left( {x - 1} \right)\left( {x + 3} \right)}}{{{x^2} - 1}}\) là:
Đáp án : C
Điều kiện xác định của phân thức là mẫu thức khác 0 .
Điều kiện xác định của phân thức \(\frac{{\left( {x - 1} \right)\left( {x + 3} \right)}}{{{x^2} - 1}}\) là: \({x^2} - 1 \ne 0\) hay \(x \ne 1,x \ne - 1\)
Đáp án C.
Chọn khẳng định sai.
Đáp án : B
Nhận biết hai tam giác đồng dạng.
Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1
Hai tam giác đều có các góc đều bằng \({60^0}\) và các cạnh tương ứng tỉ lệ nên chúng đồng dạng.
Hai tam giác cân chưa chắc đồng dạng nên \({\rm{B}}\) sai.
Đáp án B.
Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
Đáp án : B
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Ta thấy:
\(\frac{4}{{12}} = \frac{5}{{15}} = \frac{6}{{18}} = \frac{1}{3}\) nên \(A\) đúng.
\(\frac{3}{9} = \frac{4}{{12}} \ne \frac{6}{{16}}\) nên \(B\) sai.
\(\frac{2}{1} = \frac{2}{1} = \frac{2}{1}\) nên \(C\) đúng.
\(\frac{{14}}{7} = \frac{{15}}{{7,5}} = \frac{{16}}{8} = 2\) nên \(D\) đúng
Đáp án B.
Kết quả của phép chia \(\frac{{a - 2b}}{{16}}:\frac{{2a - 4b}}{{12}}\) bằng:
Đáp án : A
Muốn chia phân thức \(\frac{A}{B}\) cho phân thức \(\frac{C}{D}\) khác 0 , ta nhân \(\frac{A}{B}\) với phân thức nghịch đảo của \(\frac{C}{D}\)
\(\frac{A}{B}:\frac{C}{D} = \frac{A}{B} \cdot \frac{D}{C}\)
\(\frac{{a - 2b}}{{16}}:\frac{{2a - 4b}}{{12}} = \frac{{a - 2b}}{{16}} \cdot \frac{{12}}{{2a - 4b}} = \frac{{\left( {a - 2b} \right) \cdot 12}}{{16 \cdot \left( {2a - 4b} \right)}} = \frac{{\left( {a - 2b} \right) \cdot 12}}{{32 \cdot \left( {a - 2b} \right)}} = \frac{3}{8}\)
Đáp án A.
Nếu 2 tam giác \({\rm{ABC}}\) và \({\rm{DEF}}\) có \(\widehat A = \widehat D,\widehat C = \widehat F\) thì:
Đáp án : A
TH đồng dạng g-g: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Xét \(\Delta ABC\) và \(\Delta DEF\) có: \(\widehat A = \widehat D\left( {{\rm{gt}}} \right);\widehat C = \widehat F\left( {{\rm{gt}}} \right)\)
Suy ra $\Delta ABC\backsim \Delta DEF\left( g-g \right)$
Đáp án A.
Tổng các nghiệm của hai phương trình \( - 6\left( {1,5 - 2x} \right) = 3\left( { - 15 + 2x} \right);5x + 10 = 0\) bằng:
Đáp án : A
Giải lần lượt từng phương trình:
PT1: \( - 6\left( {1,5 - 2x} \right) = 3\left( { - 15 + 2x} \right)\)
\( - 2\left( {1,5 - 2x} \right) = - 15 + 2x\)
\( - 3 + 4x = - 15 + 2x\)
\(4x - 2x = - 15 + 3\)
\(2x = - 12\)
\(x = - 6\)
PT2: \(5x + 10 = 0\)
\(5x = - 10\)
\(x = - 2\)
Ta có tổng các nghiệm của hai phương trình trên là \( - 6 + \left( { - 2} \right) = - 8\)
Đáp án A.
Cho biết một nửa đàn bò đang gặm cỏ trên cánh đồng, \(\frac{1}{3}\) đàn bò đang nằm nghỉ gần đó, còn lại 4 con đang uống nước ở ao. Tính số bò hiện có trong đàn.
Đáp án : C
Bước 1. Lập phương trình.
Bước 3. Trả lời.
Gọi số bò có trong đàn là \({\rm{x}}\) (con). Điều kiện: \({\rm{x}} \in {\mathbb{N}^{\rm{*}}}\).
Vì một nửa đàn bò đang gặm cỏ trên cánh đồng, \(\frac{1}{3}\) đàn bò đang nằm nghỉ gần đó, còn lại 4 con đang uống nước ở ao nên ta có \({\rm{PT}}\):
\(\frac{1}{2}x + \frac{1}{3}x + 4 = x\)
\(x - \frac{1}{2}x - \frac{1}{3}x = 4\)
\(\frac{1}{6}x = 4\)
\(x = 24\left( {TM} \right)\)
Vậy đàn bò có 24 con.
Đáp án C.
Cho biểu thức: \(B = \frac{1}{{x + 1}} - \frac{{{x^3} - x}}{{{x^2} + 1}} \cdot \left( {\frac{1}{{{x^2} + 2x + 1}} - \frac{1}{{{x^2} - 1}}} \right)\) (ĐKXĐ: \(\left. {x \ne \pm 1} \right)\)
a) Rút gọn \(B\)
b) Tính giá trị của \(B\) tại \(x = - 2\)
c) Với giá trị nào của \(x\) thì \(B = 1\)
Rút gọn biểu thức bằng cách thực hiện các phép toán cộng, trừ, nhân, chia phân thức.
Tính giá trị của biểu thức tại giá trị của biến cho trước.
Tìm giá trị của biến tại giá trị của biểu thức cho trước.
a) \(B = \frac{1}{{x + 1}} - \frac{{x\left( {x - 1} \right)\left( {x + 1} \right)}}{{{x^2} + 1}} \cdot \frac{{\left( {x - 1} \right) - \left( {x + 1} \right)}}{{{{(x + 1)}^2}\left( {x - 1} \right)}}(\) ĐКXĐ: \(x \ne \pm 1)\)
\(B = \frac{1}{{x + 1}} - \frac{{ - 2x}}{{\left( {{x^2} + 1} \right)\left( {x + 1} \right)}}\)
\(B = \frac{{{x^2} + 1 + 2x}}{{\left( {{x^2} + 1} \right)\left( {x + 1} \right)}}\)
\(B = \frac{{{{(x + 1)}^2}}}{{\left( {{x^2} + 1} \right)\left( {x + 1} \right)}}\)
\(B = \frac{{x + 1}}{{{x^2} + 1}}\)
Vậy \(B = \frac{{x + 1}}{{{x^2} + 1}}\) với \(x \ne \pm 1\)
b) Thay \(x = - 2\) (TM) ta có: \(B = \frac{{ - 2 + 1}}{{{{( - 2)}^2} + 1}} = \frac{{ - 1}}{5}\)c) \(B = 1 \Rightarrow \frac{{x + 1}}{{{x^2} + 1}} = 1 \Leftrightarrow x + 1 = {x^2} + 1 \Leftrightarrow x - {x^2} = 0 \Leftrightarrow x\left( {1 - x} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0\left( {TM} \right)}\\{x = 1\left( {{\rm{\;KTM\;}}} \right)}\end{array}} \right.\)
Vậy khi \(x = 0\) thì \(B = 1\)
Giải các phương trình sau:a) \(\frac{{9x + 5}}{6} = 1 - \frac{{6 + 3x}}{8}\);b) \(\frac{{x + 1}}{4} = \frac{1}{2} + \frac{{2x + 1}}{5}\);c) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{3}{2} - \frac{{1 - 2x}}{4}\).
- Chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó (Quy tấc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
a) \(\frac{{9x + 5}}{6} = 1 - \frac{{6 + 3x}}{8}\)
\(\frac{{4\left( {9x + 5} \right)}}{{24}} = \frac{{24}}{{24}} - \frac{{3\left( {6 + 3x} \right)}}{{24}}\)
\(36x + 20 = 24 - 18 - 9x\)
\(36x + 9x = 6 - 20\)
\(45x = - 14\)\(x = \frac{{ - 14}}{{45}}\)
Vậy \(x = \frac{{ - 14}}{{45}}\)b) \(\frac{{x + 1}}{4} = \frac{1}{2} + \frac{{2x + 1}}{5}\)
\(\frac{{5(x + 1)}}{20} = \frac{10}{20} + \frac{{4(2x + 1)}}{5}\)
\(5x + 5 = 10 + 8x + 4\)\(5x - 8x = 14 - 5\)
\( - 3x = 9\)
\(x = - 3\)
Vậy \(x = - 3\)c) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{3}{2} - \frac{{1 - 2x}}{4}\)\(\frac{{8\left( {x + 1} \right)}}{{12}} = \frac{{18}}{{12}} - \frac{{3\left( {1 - 2x} \right)}}{{12}}\)\(8x + 8 = 18 - 3 + 6x\)\(8x - 6x = 15 - 8\)\(2x = 7\)\(x = \frac{7}{2}\)Vậy \(x = \frac{7}{2}\)
Tổng số học sinh khối 8 và khối 9 của một trường là 580 em, trong đó có \(256\) em là học sinh giỏi. Tính số học sinh của mỗi khối, biết rằng số học sinh giỏi khối 8 chiếm tỉ lệ \(40{\rm{\% }}\) số học sinh khối 8, số học sinh giỏi khối 9 chiếm tỉ lệ 48% số học sinh khối 9.
Bước 1. Lập phương trình.
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết.
- Lập phương trình biểu diễn mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Trả lời.
- Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không.
- Kết luận.
Gọi số học sinh khối 8 là \(x\). (học sinh). Điều kiện: \(x \in {\mathbb{N}^{\rm{*}}};x < 580\).
Số học sinh khối 9 là: \(580 - x\) (học sinh).
học sinh giỏi khối 8 là: \(40{\rm{\% }}x = 0,4x\) (học sinh)
Số học sinh giỏi khối 9 là: \(48%.\left( 580-x \right)=0,48.\left( 580-x \right)\) (học sinh)
Vì cả hai khối có tổng cả 256 học sinh giỏi nên ta có phương trình:
\(0,4x + 0,48\left( {580 - x} \right) = 256\)
\(0,4x + 278,4 - 0,48x = 256\)
\(0,4x - 0,48x = 256 - 278,4\)
\( - 0,08x = - 22,4\)
\(x = \left( { - 22,4} \right):\left( { - 0,08} \right)\)
\(x = 280\left( {{\rm{tm}}} \right)\)
Khi đó, số học sinh khối 9 là: \(580 - 280 = 300\) (học sinh)
Vậy khối 8 có 280 học sinh và khối 9 có 300 học sinh.
Cho \(\Delta ABC\) có các đường cao \({\rm{BD}}\) và \({\rm{CE}}\) cắt nhau tại \({\rm{H}}\). Chứng minh:a) \(\Delta HBE\) đồng dạng với \(\Delta HCD\).b) \(\widehat {HDE} = \widehat {HAE}\).
Chứng minh các cặp tam giác đồng dạng, từ đó rút ra dữ kiện cần thiết để chứng minh yêu cầu của bài toán.
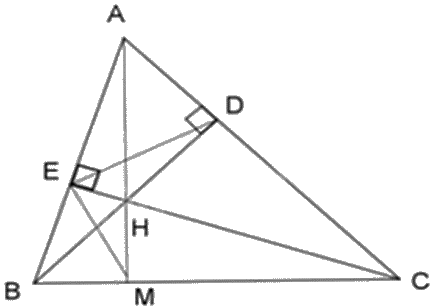
a) Xét \(\Delta HBE\) và \(\Delta HCD\) có:
\(\widehat {BDC} = \widehat {CEB} = {90^0}\)
\(\widehat {EHB} = \widehat {DHC}\) (2 góc đối đỉnh)
Suy ra $\Delta HBE\backsim \Delta HCD\left( g-g \right)$ (điều phải chứng minh)
b) Theo câu a) ta có: $\Delta HBE\backsim \Delta HCD$ suy ra \(\frac{{HE}}{{HD}} = \frac{{HB}}{{HC}}\) hay \(\frac{{HE}}{{HB}} = \frac{{HD}}{{HC}}\)
Xét \(\Delta HED\) và \(\Delta HBC\) ta có:
\(\frac{{HE}}{{HB}} = \frac{{HD}}{{HC}}\) (cmt)
\(\widehat {EHD} = \widehat {BHC}\) (hai góc đối đỉnh)
\(\widehat {HDE} = \widehat {HAE}\)
Suy ra $\Delta HED\backsim \Delta HBC\left( c-g-c \right).$
Mà đường cao \({\rm{BD}}\) và \({\rm{CE}}\) cắt nhau tại \({\rm{H}}\) (theo giả thiết)
Suy ra H là trực tâm của \(\Delta ABC\) hay \(AH \bot BC\) tại M suy ra \(\widehat {AMB} = {90^ \circ }\).
Xét \(\Delta AMB\) và \(\Delta CEB\) có:
\(\widehat {CEB} = \widehat {AMB} = {90^0}\)
\(\widehat B\) chung
Suy ra $\Delta AMB\backsim \Delta CEB\left( g-g \right)$
Suy ra \(\widehat {MAB} = \widehat {ECB}\) hay \(\widehat {HAE} = \widehat {HCB}\) (2)
Từ (1) và (2) ta có: \(\widehat {HDE} = \widehat {HAE}\) (điều phải chứng minh)
Cho \(\frac{a}{{b + c}} + \frac{b}{{c + a}} + \frac{c}{{a + b}} = 1\). Chứng minh \(\frac{{{a^2}}}{{b + c}} + \frac{{{b^2}}}{{c + a}} + \frac{{{c^2}}}{{a + b}} = 0\)
Nhân cả 2 vế của \(\frac{a}{{b + c}} + \frac{b}{{c + a}} + \frac{c}{{a + b}} = 1\) với \(a + b + c\) rồi thu gọn được điều phải chứng minh
Nhân cả 2 vế của \(\frac{a}{{b + c}} + \frac{b}{{c + a}} + \frac{a}{{a + b}} = 1\) với \(a + b + c\) ta được
\(\frac{{{\rm{a}}\left( {{\rm{a}} + {\rm{b}} + {\rm{c}}} \right)}}{{{\rm{b}} + {\rm{c}}}} + \frac{{{\rm{b}}\left( {{\rm{a}} + {\rm{b}} + {\rm{c}}} \right)}}{{{\rm{c}} + {\rm{a}}}} + \frac{{{\rm{c}}\left( {{\rm{a}} + {\rm{b}} + {\rm{c}}} \right)}}{{{\rm{a}} + {\rm{b}}}} = {\rm{a}} + {\rm{b}} + {\rm{c}}\)
\(\frac{{{a^2} + a\left( {b + c} \right)}}{{b + c}} + \frac{{{b^2} + b\left( {c + a} \right)}}{{c + a}} + \frac{{{c^2} + c\left( {a + b} \right)}}{{a + b}} = a + b + c\)
\(\frac{{{a^2}}}{{b + c}} + a + \frac{{{b^2}}}{{c + a}} + b + \frac{{{c^2}}}{{a + b}} + c = a + b + c\)
\(\frac{{{{\rm{a}}^2}}}{{{\rm{\;b}} + {\rm{c}}}} + \frac{{{{\rm{b}}^2}}}{{{\rm{c}} + {\rm{a}}}} + \frac{{{{\rm{c}}^2}}}{{{\rm{a}} + {\rm{b}}}} = 0\left( {{\rm{dpcm}}} \right)\)
Đề thi giữa kì 2 Toán 8 - Đề số 8 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong học kì. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như đa thức, phân thức đại số, phương trình bậc nhất một ẩn, hệ phương trình bậc nhất hai ẩn, bất phương trình bậc nhất một ẩn, và ứng dụng thực tế của các kiến thức này.
Thông thường, đề thi giữa kì 2 Toán 8 - Đề số 8 - Kết nối tri thức sẽ có cấu trúc gồm các phần sau:
Để giải các bài tập về đa thức, học sinh cần nắm vững các quy tắc về thu gọn đa thức, cộng trừ đa thức, nhân đa thức, chia đa thức, và phân tích đa thức thành nhân tử. Ví dụ, để thu gọn đa thức, ta cần thực hiện các phép toán cộng trừ các đơn thức đồng dạng. Để phân tích đa thức thành nhân tử, ta có thể sử dụng các phương pháp như đặt nhân tử chung, sử dụng hằng đẳng thức, hoặc nhóm các số hạng.
Để giải phương trình bậc nhất một ẩn, ta cần thực hiện các phép biến đổi tương đương để đưa phương trình về dạng x = a, trong đó a là một số thực. Các phép biến đổi tương đương bao gồm cộng hoặc trừ hai vế của phương trình cùng một số, nhân hoặc chia hai vế của phương trình cùng một số khác 0.
Để giải hệ phương trình bậc nhất hai ẩn, ta có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số. Phương pháp thế là thay một ẩn trong một phương trình bằng biểu thức của ẩn đó trong phương trình còn lại. Phương pháp cộng đại số là cộng hoặc trừ hai phương trình để loại bỏ một ẩn.
Để đạt kết quả tốt trong kỳ thi giữa kì 2 Toán 8, học sinh cần luyện tập thường xuyên và ôn tập đầy đủ các kiến thức đã học. Giaitoan.edu.vn cung cấp một nguồn tài liệu phong phú và đa dạng, bao gồm các đề thi thử, bài tập trắc nghiệm, bài tập tự luận, và các video hướng dẫn giải bài tập. Ngoài ra, học sinh cũng nên tham gia các diễn đàn toán học trực tuyến để trao đổi kiến thức và kinh nghiệm với các bạn học sinh khác.
Trước khi làm bài thi, học sinh nên đọc kỹ đề bài, xác định rõ yêu cầu của từng câu hỏi, và lập kế hoạch giải bài một cách hợp lý. Trong quá trình làm bài, học sinh nên trình bày lời giải một cách rõ ràng, mạch lạc, và kiểm tra lại kết quả trước khi nộp bài.