Chào mừng các em học sinh lớp 8 đến với đề thi giữa kì 1 Toán 8 - Đề số 2 chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn đầu năm học.
Giaitoan.edu.vn cung cấp đề thi chính thức, đáp án chi tiết và lời giải bài tập để các em có thể tự học và nâng cao kết quả học tập.
Phần trắc nghiệm (3 điểm) Câu 1: Cho các biểu thức (2x + y + {x^2}y; - 3x{y^2}{z^3} + frac{1}{2}{x^2}{y^2}z;frac{{x + y}}{{x - y}}). Có bao nhiêu đa thức trong các biểu thức trên?
Phần trắc nghiệm (3 điểm)
Câu 1: Cho các biểu thức \(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z;\frac{{x + y}}{{x - y}}\). Có bao nhiêu đa thức trong các biểu thức trên?
A. 0.
B. 1.
C. 2.
D. 3.
Câu 2: Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
A. \(14{x^2}y + 10{x^3}{y^2}\).
B. \( - 14{x^2}y + 10{x^3}{y^2}\).
C. \(6{x^2}y - 10{x^3}{y^2}\).
D. \( - 6{x^2}y + 10{x^3}{y^2}\).
Câu 3: Đơn thức thích hợp điền vào chỗ trống của ... – 9 = (5x + 3)(5x – 3) là
A. \( - 25{x^2}\).
B. \(5{x^2}\).
C. \(5x\).
D. \(25{x^2}\).
Câu 4: Biểu thức nào dưới đây là bình phương thiếu của tổng hai biểu thức x và 2y
A. \({x^2} + 2xy + 4{y^2}\).
B. \({x^2} - 2xy + 4{y^2}\).
C. \({x^2} - 4xy + 4{y^2}\).
D. \({x^2} + 4xy + 4{y^2}\).
Câu 5: Tứ giác ABCD có \(\widehat A = {100^0};\widehat B = {70^0};\widehat C = {110^0}\) thì
A. \(\widehat D = {150^0}\).
B. \(\widehat D = {90^0}\).
C. \(\widehat D = {80^0}\).
D. \(\widehat D = {50^0}\).
Câu 6: Tính giá trị biểu thức \(x(x - y) + y(x + y)\) tại \(x = 6\) và \(y = 8\) là
A. 14.
B. 7.
C. -100.
D. 100.
Câu 7: Hình nào sau đây là tứ giác có hai góc kề một đáy bằng nhau?
A. Hình thang.
B. Hình thang cân.
C. Hình thang vuông.
D. Hình bình hành.
Câu 8: Với giá trị nào của a thì biểu thức \({x^2} + 4x + a\) viết được dưới dạng bình phương của một tổng
A. a = 1.
B. a = 9.
C. a = 16.
D. a = 4.
Câu 9: Giá trị của biểu thức: \({x^2} - 8x + 16\) tại x = 4 là
A. 0.
B. 4.
C. -16.
D. 16.
Câu 10: Trong giờ học Mỹ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là x (cm), y (cm) như hình bên. Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là
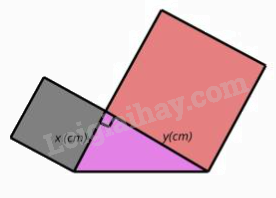
A. 41,5 cm2.
B. 40,5 cm2.
C. 44 cm2.
D. 47,2 cm2.
Câu 11: Kết quả thương của phép chia \(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2}\) là
A. 12.
B. 24.
C. 24x2y.
D. 12x2y.
Câu 12: Hình chữ nhật có hai đường chéo vuông góc là
A. hình chữ nhật.
B. hình thoi.
C. hình vuông.
D. hình thang.
Phần tự luận (7 điểm)
Bài 1. (2 điểm) Rút gọn rồi tính giá trị của biểu thức
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right)\) tại \(x = \frac{{ - 1}}{2}\) và \(y = 4\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right)\) tại \(x = \frac{1}{2}\) và \(y = 2\).
Bài 2. (2 điểm)
1) Tìm x, biết:
a) \(2{x^2} + x = 0\)
b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\)
2) Tính nhanh: \({34^2} + {16^2} + 32.34\)
Bài 3. (2,5 điểm) Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với BD tại F, cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) Chứng minh AF // CE.
c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.
Bài 4. (0,5 điểm) Chứng minh rằng \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
-------- Hết --------
Phần trắc nghiệm (3 điểm)
1. C | 2. D | 3. D | 4. A | 5. C | 6. D |
7. B | 8. D | 9. A | 10. A | 11. B | 12. C |
Câu 1: Cho các biểu thức \(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z;\frac{{x + y}}{{x - y}}\). Có bao nhiêu đa thức trong các biểu thức trên?
A. 0. | B. 1. |
C. 2. | D. 3. |
Phương pháp
Dựa vào khái niệm đa thức: Đa thức là tổng của những đơn thức; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Lời giải
\(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z\) là những đa thức vì là tổng của những đơn thức.
\(\frac{{x + y}}{{x - y}}\) không phải đa thức.
Đáp án C.
Câu 2: Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
A. \(14{x^2}y + 10{x^3}{y^2}\). | B. \( - 14{x^2}y + 10{x^3}{y^2}\). |
C. \(6{x^2}y - 10{x^3}{y^2}\). | D. \( - 6{x^2}y + 10{x^3}{y^2}\). |
Phương pháp
Cộng, trừ các hạng tử đồng dạng để rút gọn.
Lời giải
\(\begin{array}{l}4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\\ = \left( {4{x^2}y - 10{x^2}y} \right) + \left( {6{x^3}{y^2} + 4{x^3}{y^2}} \right)\\ = - 6{x^2}y + 10{x^3}{y^2}\end{array}\)
Đáp án D.
Câu 3: Đơn thức thích hợp điền vào chỗ trống của ... – 9 = (5x + 3)(5x – 3) là
A. \( - 25{x^2}\). | B. \(5{x^2}\). |
C. \(5x\). | D. \(25{x^2}\). |
Phương pháp
Sử dụng công thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\).
Lời giải
\(\left( {5x + 3} \right)\left( {5x - 3} \right) = {\left( {5x} \right)^2} - {3^2} = 25{x^2} - 9\).
Vậy đơn thức điền vào chỗ trống là 25x2.
Đáp án D.
Câu 4: Biểu thức nào dưới đây là bình phương thiếu của tổng hai biểu thức x và 2y
A. \({x^2} + 2xy + 4{y^2}\). | B. \({x^2} - 2xy + 4{y^2}\). |
C. \({x^2} - 4xy + 4{y^2}\). | D. \({x^2} + 4xy + 4{y^2}\). |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
Bình phương thiếu của tổng hai biểu thức x và 2y là \({x^2} + 2xy + 4{y^2}\).
Đáp án A.
Câu 5: Tứ giác ABCD có \(\widehat A = {100^0};\widehat B = {70^0};\widehat C = {110^0}\) thì
A.\(\widehat D = {150^0}\). | B. \(\widehat D = {90^0}\). |
C. \(\widehat D = {80^0}\). | D. \(\widehat D = {50^0}\). |
Phương pháp
Dựa vào tổng các góc của một tứ giác là 3600.
Lời giải
Xét tứ giác ABCD ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{100^0} + {70^0} + {110^0} + \widehat D = {360^0}\\{280^0} + \widehat D = {360^0}\\\widehat D = {80^0}\end{array}\)
Đáp án C.
Câu 6: Tính giá trị biểu thức \(x(x - y) + y(x + y)\) tại \(x = 6\) và \(y = 8\) là
A. 14. | B. 7. |
C. -100. | D. 100. |
Phương pháp
Rút gọn biểu thức sau đó thay giá trị x, y vào biểu thức.
Lời giải
\(x(x - y) + y(x + y) = {x^2} - xy + xy + {y^2} = {x^2} + {y^2}\).
Thay \(x = 6\) và \(y = 8\) vào biểu thức, ta được: \({6^2} + {8^2} = 100\).
Đáp án D.
Câu 7: Hình nào sau đây là tứ giác có hai góc kề một đáy bằng nhau?
A. Hình thang. | B. Hình thang cân. |
C. Hình thang vuông. | D. Hình bình hành. |
Phương pháp
Dựa vào kiến thức các hình đã học.
Lời giải
Hình có hai góc kề một đáy bằng nhau là hình thang cân.
Đáp án B.
Câu 8: Với giá trị nào của a thì biểu thức \({x^2} + 4x + a\) viết được dưới dạng bình phương của một tổng
A. a = 1. | B. a = 9. |
C. a = 16. | D. a = 4. |
Phương pháp
Dựa vào kiến thức về hằng đẳng thức.
Lời giải
Ta có:
\(\begin{array}{l}{\left( {x + 2} \right)^2} = {x^2} + 2.2x + {2^2} = {x^2} + 4x + 4\\ \Rightarrow a = 4\end{array}\)
Đáp án D.
Câu 9: Giá trị của biểu thức: \({x^2} - 8x + 16\) tại x = 4 là
A. 0. | B. 4. |
C. -16. | D. 16. |
Phương pháp
Đưa biểu thức về bình phương của một hiệu, thay x = 4 để tính giá trị.
Lời giải
\({x^2} - 8x + 16 = {x^2} - 2.4.x + {4^2} = {\left( {x - 4} \right)^2}\).
Thay x = 4 vào biểu thức ta được: \({(4 - 4)^2} = {0^2} = 0\).
Đáp án a.
Câu 10: Trong giờ học Mỹ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là x (cm), y (cm) như hình bên. Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là
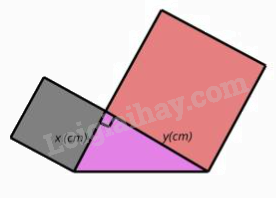
A. 41,5 cm2. | B. 40,5 cm2. |
C. 44 cm2. | D. 47,2 cm2. |
Phương pháp
Dựa vào công thức tính diện tích hình vuông, diện tích hình tam giác.
Lời giải
Diện tích hai hình vuông là: \({x^2} + {y^2} = {3^2} + {5^2} = 34\)(cm2).
Diện tích hình tam giác vuông là: \(\frac{{x.y}}{2} = \frac{{3.5}}{2} = \frac{{15}}{2} = 7,5\)(cm2).
Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là: 34 + 7,5 = 41,5 (cm2).
Đáp án A.
Câu 11: Kết quả thương của phép chia \(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2}\) là
A. 12. | B. 24. |
C. 24x2y. | D. 12x2y. |
Phương pháp
Dựa vào quy tắc chia đơn thức cho đơn thức.
Lời giải
\(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2} = 6{x^4}{y^2}:\frac{1}{4}{x^4}{y^2} = \left( {6:\frac{1}{4}} \right)\left( {{x^4}:{x^4}} \right)\left( {{y^2}:{y^2}} \right) = 24\)
Đáp án B.
Câu 12: Hình chữ nhật có hai đường chéo vuông góc là
A. hình chữ nhật. | B. hình thoi. |
C. hình vuông. | D. hình thang. |
Phương pháp
Dựa vào dấu hiệu nhận biết hình đã học.
Lời giải
Hình chữ nhật có hai đường chéo vuông góc là hình vuông.
Đáp án C.
Phần tự luận. (7 điểm)
Bài 1. (2 điểm) Rút gọn rồi tính giá trị của biểu thưc
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right)\) tại \(x = \frac{{ - 1}}{2}\) và \(y = 4\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right)\) tại \(x = \frac{1}{2}\) và \(y = 2\).
Phương pháp
+ Sử dụng quy tắc cộng, trừ, nhân, chia đa thức và những hằng đẳng thức đáng nhớ để rút gọn.
+ Thay x, y vào để tính giá trị.
Lời giải
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right) = {\left( {2x} \right)^2} - {\left( {\frac{1}{2}y} \right)^2} = 4{x^2} - \frac{1}{4}{y^2}\)
Thay \(x = \frac{{ - 1}}{2}\) và \(y = 4\) vào M ta được:
\(4{\left( {\frac{{ - 1}}{2}} \right)^2} - \frac{1}{4}{.4^2} = 4.\frac{1}{4} - \frac{1}{4}.16 = 1 - 4 = - 3\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right) = {\left( {2x} \right)^3} - {\left( {{y^2}} \right)^3} = 8{x^3} - {y^6}\)
Thay \(x = \frac{1}{2}\) và \(y = 2\) vào N ta được:
\(8{\left( {\frac{1}{2}} \right)^3} - {2^6} = 8.\frac{1}{8} - 64 = 1 - 64 = - 63\).
Bài 2. (2 điểm)
1) Tìm x, biết:
a) \(2{x^2} + x = 0\) | b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\) |
2) Tính nhanh: \({34^2} + {16^2} + 32.34\)
Phương pháp
1) Phân tích đa thức thành nhân tử để tìm x.
2) Dựa vào hằng đẳng thức đáng nhớ để tính.
Lời giải
1)
a) \(2{x^2} + x = 0\)
\(\begin{array}{l}x(2x + 1) = 0\\\left[ \begin{array}{l}x = 0\\2x + 1 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = \frac{{ - 1}}{2}\end{array} \right.\end{array}\)
Vậy \(x = 0\) hoặc \(x = \frac{{ - 1}}{2}\).
b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\)
\(\begin{array}{l}x(2x - 10) - x(3 + 2x) = 26\\x(2x - 10 - 3 - 2x) = 26\\x.( - 13) = 26\\x = - 2\end{array}\)
Vậy x = -2.
2) \({34^2} + {16^2} + 32.34\) = 342 + 162 + 2.16.34 = (34 + 16)2 = 502 = 2500.
Bài 3. (2,5 điểm) Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với BD tại F, cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) Chứng minh AF // CE.
c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.
Phương pháp
a) Chứng minh tứ giác AKCI có hai cặp cạnh đối song song nên là hình bình hành.
b) Chứng minh AECF là hình bình hành suy ra AF // CE (2 cặp cạnh đối song song).
c) Chứng minh giao điểm của AC với EF và giao điểm của AC với KI trùng nhau.
Lời giải
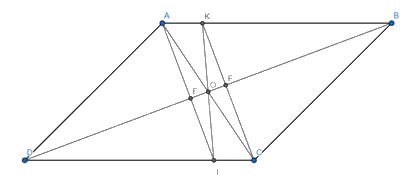
a) Vì ABCD là hình bình hành nên AB // CD. Do đó: AK // IC.
Mặt khác, \(AI \bot BD\) và \(CK \bot BD\). Nên AI // CK.
Vì vậy: AICK là hình bình hành (tứ giác có hai cặp cạnh đối song song).
b) Vì ABCD là hình bình hành nên AB // CD.
Xét \(\Delta ABE\) và \(\Delta CDF\) có:
\(\widehat {AEB} = \widehat {CFD}\left( { = {{90}^0}} \right)\)
\(\widehat {ABE} = \widehat {CDF}\) (so le trong)
AB = CD
Do đó \(\Delta ABE = \Delta CDF\)(ch – gn)
Suy ra AE = CF (cạnh tương ứng).
Mà AE // CF nên AECF là hình bình hành (Tứ giác có cặp cạnh đối song song và bằng nhau).
Do đó AF // CE.
c) Ta có: AICK là hình bình hành (cmt). Gọi O là giao điểm của hai đường chéo AC và KI. Khi đó O là trung điểm của AC và O là trung điểm của KI. (1)
Tương tự, AECF là hình bình hành (cmt). Gọi O’ là giao điểm của hai đường chéo AC và EF. Khi đó O’ là trung điểm của AC và O’ là trung điểm của EF. (2)
Từ (1) và (2) suy ra O và O’ trung nhau. Hay AC, EF và KI đồng quy tại một điểm.
Bài 4. (0,5 điểm) Chứng minh rằng \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
Phương pháp
Dựa vào hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) để chứng minh.
Lời giải
Ta có:
\(\begin{array}{l}9 - {\left( {1 + 4k} \right)^2} = {3^2} - {\left( {1 + 4k} \right)^2} = \left( {3 - 1 - 4k} \right)\left( {3 + 1 + 4k} \right)\\ = \left( {2 - 4k} \right)\left( {4 + 4k} \right) = 2.4\left( {1 - 2k} \right)\left( {1 + k} \right) = 8\left( {1 - 2k} \right)\left( {1 + k} \right) \vdots 8\forall k \in \mathbb{Z}\end{array}\)
Vậy \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
Tải về
Phần trắc nghiệm (3 điểm)
Câu 1: Cho các biểu thức \(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z;\frac{{x + y}}{{x - y}}\). Có bao nhiêu đa thức trong các biểu thức trên?
A. 0.
B. 1.
C. 2.
D. 3.
Câu 2: Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
A. \(14{x^2}y + 10{x^3}{y^2}\).
B. \( - 14{x^2}y + 10{x^3}{y^2}\).
C. \(6{x^2}y - 10{x^3}{y^2}\).
D. \( - 6{x^2}y + 10{x^3}{y^2}\).
Câu 3: Đơn thức thích hợp điền vào chỗ trống của ... – 9 = (5x + 3)(5x – 3) là
A. \( - 25{x^2}\).
B. \(5{x^2}\).
C. \(5x\).
D. \(25{x^2}\).
Câu 4: Biểu thức nào dưới đây là bình phương thiếu của tổng hai biểu thức x và 2y
A. \({x^2} + 2xy + 4{y^2}\).
B. \({x^2} - 2xy + 4{y^2}\).
C. \({x^2} - 4xy + 4{y^2}\).
D. \({x^2} + 4xy + 4{y^2}\).
Câu 5: Tứ giác ABCD có \(\widehat A = {100^0};\widehat B = {70^0};\widehat C = {110^0}\) thì
A. \(\widehat D = {150^0}\).
B. \(\widehat D = {90^0}\).
C. \(\widehat D = {80^0}\).
D. \(\widehat D = {50^0}\).
Câu 6: Tính giá trị biểu thức \(x(x - y) + y(x + y)\) tại \(x = 6\) và \(y = 8\) là
A. 14.
B. 7.
C. -100.
D. 100.
Câu 7: Hình nào sau đây là tứ giác có hai góc kề một đáy bằng nhau?
A. Hình thang.
B. Hình thang cân.
C. Hình thang vuông.
D. Hình bình hành.
Câu 8: Với giá trị nào của a thì biểu thức \({x^2} + 4x + a\) viết được dưới dạng bình phương của một tổng
A. a = 1.
B. a = 9.
C. a = 16.
D. a = 4.
Câu 9: Giá trị của biểu thức: \({x^2} - 8x + 16\) tại x = 4 là
A. 0.
B. 4.
C. -16.
D. 16.
Câu 10: Trong giờ học Mỹ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là x (cm), y (cm) như hình bên. Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là
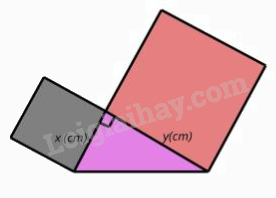
A. 41,5 cm2.
B. 40,5 cm2.
C. 44 cm2.
D. 47,2 cm2.
Câu 11: Kết quả thương của phép chia \(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2}\) là
A. 12.
B. 24.
C. 24x2y.
D. 12x2y.
Câu 12: Hình chữ nhật có hai đường chéo vuông góc là
A. hình chữ nhật.
B. hình thoi.
C. hình vuông.
D. hình thang.
Phần tự luận (7 điểm)
Bài 1. (2 điểm) Rút gọn rồi tính giá trị của biểu thức
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right)\) tại \(x = \frac{{ - 1}}{2}\) và \(y = 4\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right)\) tại \(x = \frac{1}{2}\) và \(y = 2\).
Bài 2. (2 điểm)
1) Tìm x, biết:
a) \(2{x^2} + x = 0\)
b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\)
2) Tính nhanh: \({34^2} + {16^2} + 32.34\)
Bài 3. (2,5 điểm) Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với BD tại F, cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) Chứng minh AF // CE.
c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.
Bài 4. (0,5 điểm) Chứng minh rằng \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
-------- Hết --------
Phần trắc nghiệm (3 điểm)
1. C | 2. D | 3. D | 4. A | 5. C | 6. D |
7. B | 8. D | 9. A | 10. A | 11. B | 12. C |
Câu 1: Cho các biểu thức \(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z;\frac{{x + y}}{{x - y}}\). Có bao nhiêu đa thức trong các biểu thức trên?
A. 0. | B. 1. |
C. 2. | D. 3. |
Phương pháp
Dựa vào khái niệm đa thức: Đa thức là tổng của những đơn thức; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Lời giải
\(2x + y + {x^2}y; - 3x{y^2}{z^3} + \frac{1}{2}{x^2}{y^2}z\) là những đa thức vì là tổng của những đơn thức.
\(\frac{{x + y}}{{x - y}}\) không phải đa thức.
Đáp án C.
Câu 2: Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
A. \(14{x^2}y + 10{x^3}{y^2}\). | B. \( - 14{x^2}y + 10{x^3}{y^2}\). |
C. \(6{x^2}y - 10{x^3}{y^2}\). | D. \( - 6{x^2}y + 10{x^3}{y^2}\). |
Phương pháp
Cộng, trừ các hạng tử đồng dạng để rút gọn.
Lời giải
\(\begin{array}{l}4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\\ = \left( {4{x^2}y - 10{x^2}y} \right) + \left( {6{x^3}{y^2} + 4{x^3}{y^2}} \right)\\ = - 6{x^2}y + 10{x^3}{y^2}\end{array}\)
Đáp án D.
Câu 3: Đơn thức thích hợp điền vào chỗ trống của ... – 9 = (5x + 3)(5x – 3) là
A. \( - 25{x^2}\). | B. \(5{x^2}\). |
C. \(5x\). | D. \(25{x^2}\). |
Phương pháp
Sử dụng công thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\).
Lời giải
\(\left( {5x + 3} \right)\left( {5x - 3} \right) = {\left( {5x} \right)^2} - {3^2} = 25{x^2} - 9\).
Vậy đơn thức điền vào chỗ trống là 25x2.
Đáp án D.
Câu 4: Biểu thức nào dưới đây là bình phương thiếu của tổng hai biểu thức x và 2y
A. \({x^2} + 2xy + 4{y^2}\). | B. \({x^2} - 2xy + 4{y^2}\). |
C. \({x^2} - 4xy + 4{y^2}\). | D. \({x^2} + 4xy + 4{y^2}\). |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
Bình phương thiếu của tổng hai biểu thức x và 2y là \({x^2} + 2xy + 4{y^2}\).
Đáp án A.
Câu 5: Tứ giác ABCD có \(\widehat A = {100^0};\widehat B = {70^0};\widehat C = {110^0}\) thì
A.\(\widehat D = {150^0}\). | B. \(\widehat D = {90^0}\). |
C. \(\widehat D = {80^0}\). | D. \(\widehat D = {50^0}\). |
Phương pháp
Dựa vào tổng các góc của một tứ giác là 3600.
Lời giải
Xét tứ giác ABCD ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{100^0} + {70^0} + {110^0} + \widehat D = {360^0}\\{280^0} + \widehat D = {360^0}\\\widehat D = {80^0}\end{array}\)
Đáp án C.
Câu 6: Tính giá trị biểu thức \(x(x - y) + y(x + y)\) tại \(x = 6\) và \(y = 8\) là
A. 14. | B. 7. |
C. -100. | D. 100. |
Phương pháp
Rút gọn biểu thức sau đó thay giá trị x, y vào biểu thức.
Lời giải
\(x(x - y) + y(x + y) = {x^2} - xy + xy + {y^2} = {x^2} + {y^2}\).
Thay \(x = 6\) và \(y = 8\) vào biểu thức, ta được: \({6^2} + {8^2} = 100\).
Đáp án D.
Câu 7: Hình nào sau đây là tứ giác có hai góc kề một đáy bằng nhau?
A. Hình thang. | B. Hình thang cân. |
C. Hình thang vuông. | D. Hình bình hành. |
Phương pháp
Dựa vào kiến thức các hình đã học.
Lời giải
Hình có hai góc kề một đáy bằng nhau là hình thang cân.
Đáp án B.
Câu 8: Với giá trị nào của a thì biểu thức \({x^2} + 4x + a\) viết được dưới dạng bình phương của một tổng
A. a = 1. | B. a = 9. |
C. a = 16. | D. a = 4. |
Phương pháp
Dựa vào kiến thức về hằng đẳng thức.
Lời giải
Ta có:
\(\begin{array}{l}{\left( {x + 2} \right)^2} = {x^2} + 2.2x + {2^2} = {x^2} + 4x + 4\\ \Rightarrow a = 4\end{array}\)
Đáp án D.
Câu 9: Giá trị của biểu thức: \({x^2} - 8x + 16\) tại x = 4 là
A. 0. | B. 4. |
C. -16. | D. 16. |
Phương pháp
Đưa biểu thức về bình phương của một hiệu, thay x = 4 để tính giá trị.
Lời giải
\({x^2} - 8x + 16 = {x^2} - 2.4.x + {4^2} = {\left( {x - 4} \right)^2}\).
Thay x = 4 vào biểu thức ta được: \({(4 - 4)^2} = {0^2} = 0\).
Đáp án a.
Câu 10: Trong giờ học Mỹ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là x (cm), y (cm) như hình bên. Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là
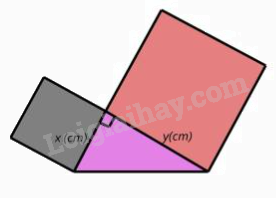
A. 41,5 cm2. | B. 40,5 cm2. |
C. 44 cm2. | D. 47,2 cm2. |
Phương pháp
Dựa vào công thức tính diện tích hình vuông, diện tích hình tam giác.
Lời giải
Diện tích hai hình vuông là: \({x^2} + {y^2} = {3^2} + {5^2} = 34\)(cm2).
Diện tích hình tam giác vuông là: \(\frac{{x.y}}{2} = \frac{{3.5}}{2} = \frac{{15}}{2} = 7,5\)(cm2).
Tổng diện tích của hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là: 34 + 7,5 = 41,5 (cm2).
Đáp án A.
Câu 11: Kết quả thương của phép chia \(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2}\) là
A. 12. | B. 24. |
C. 24x2y. | D. 12x2y. |
Phương pháp
Dựa vào quy tắc chia đơn thức cho đơn thức.
Lời giải
\(6{x^4}{y^2}:{\left( {\frac{1}{2}{x^2}y} \right)^2} = 6{x^4}{y^2}:\frac{1}{4}{x^4}{y^2} = \left( {6:\frac{1}{4}} \right)\left( {{x^4}:{x^4}} \right)\left( {{y^2}:{y^2}} \right) = 24\)
Đáp án B.
Câu 12: Hình chữ nhật có hai đường chéo vuông góc là
A. hình chữ nhật. | B. hình thoi. |
C. hình vuông. | D. hình thang. |
Phương pháp
Dựa vào dấu hiệu nhận biết hình đã học.
Lời giải
Hình chữ nhật có hai đường chéo vuông góc là hình vuông.
Đáp án C.
Phần tự luận. (7 điểm)
Bài 1. (2 điểm) Rút gọn rồi tính giá trị của biểu thưc
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right)\) tại \(x = \frac{{ - 1}}{2}\) và \(y = 4\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right)\) tại \(x = \frac{1}{2}\) và \(y = 2\).
Phương pháp
+ Sử dụng quy tắc cộng, trừ, nhân, chia đa thức và những hằng đẳng thức đáng nhớ để rút gọn.
+ Thay x, y vào để tính giá trị.
Lời giải
a) \(M = \left( {2x - \frac{1}{2}y} \right)\left( {2x + \frac{1}{2}y} \right) = {\left( {2x} \right)^2} - {\left( {\frac{1}{2}y} \right)^2} = 4{x^2} - \frac{1}{4}{y^2}\)
Thay \(x = \frac{{ - 1}}{2}\) và \(y = 4\) vào M ta được:
\(4{\left( {\frac{{ - 1}}{2}} \right)^2} - \frac{1}{4}{.4^2} = 4.\frac{1}{4} - \frac{1}{4}.16 = 1 - 4 = - 3\).
b) \(N = \left( {2x - {y^2}} \right)\left( {4{x^2} + 2x{y^2} + {y^4}} \right) = {\left( {2x} \right)^3} - {\left( {{y^2}} \right)^3} = 8{x^3} - {y^6}\)
Thay \(x = \frac{1}{2}\) và \(y = 2\) vào N ta được:
\(8{\left( {\frac{1}{2}} \right)^3} - {2^6} = 8.\frac{1}{8} - 64 = 1 - 64 = - 63\).
Bài 2. (2 điểm)
1) Tìm x, biết:
a) \(2{x^2} + x = 0\) | b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\) |
2) Tính nhanh: \({34^2} + {16^2} + 32.34\)
Phương pháp
1) Phân tích đa thức thành nhân tử để tìm x.
2) Dựa vào hằng đẳng thức đáng nhớ để tính.
Lời giải
1)
a) \(2{x^2} + x = 0\)
\(\begin{array}{l}x(2x + 1) = 0\\\left[ \begin{array}{l}x = 0\\2x + 1 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = \frac{{ - 1}}{2}\end{array} \right.\end{array}\)
Vậy \(x = 0\) hoặc \(x = \frac{{ - 1}}{2}\).
b) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\)
\(\begin{array}{l}x(2x - 10) - x(3 + 2x) = 26\\x(2x - 10 - 3 - 2x) = 26\\x.( - 13) = 26\\x = - 2\end{array}\)
Vậy x = -2.
2) \({34^2} + {16^2} + 32.34\) = 342 + 162 + 2.16.34 = (34 + 16)2 = 502 = 2500.
Bài 3. (2,5 điểm) Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với BD tại F, cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) Chứng minh AF // CE.
c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.
Phương pháp
a) Chứng minh tứ giác AKCI có hai cặp cạnh đối song song nên là hình bình hành.
b) Chứng minh AECF là hình bình hành suy ra AF // CE (2 cặp cạnh đối song song).
c) Chứng minh giao điểm của AC với EF và giao điểm của AC với KI trùng nhau.
Lời giải
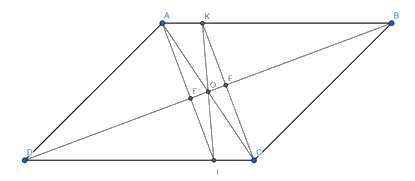
a) Vì ABCD là hình bình hành nên AB // CD. Do đó: AK // IC.
Mặt khác, \(AI \bot BD\) và \(CK \bot BD\). Nên AI // CK.
Vì vậy: AICK là hình bình hành (tứ giác có hai cặp cạnh đối song song).
b) Vì ABCD là hình bình hành nên AB // CD.
Xét \(\Delta ABE\) và \(\Delta CDF\) có:
\(\widehat {AEB} = \widehat {CFD}\left( { = {{90}^0}} \right)\)
\(\widehat {ABE} = \widehat {CDF}\) (so le trong)
AB = CD
Do đó \(\Delta ABE = \Delta CDF\)(ch – gn)
Suy ra AE = CF (cạnh tương ứng).
Mà AE // CF nên AECF là hình bình hành (Tứ giác có cặp cạnh đối song song và bằng nhau).
Do đó AF // CE.
c) Ta có: AICK là hình bình hành (cmt). Gọi O là giao điểm của hai đường chéo AC và KI. Khi đó O là trung điểm của AC và O là trung điểm của KI. (1)
Tương tự, AECF là hình bình hành (cmt). Gọi O’ là giao điểm của hai đường chéo AC và EF. Khi đó O’ là trung điểm của AC và O’ là trung điểm của EF. (2)
Từ (1) và (2) suy ra O và O’ trung nhau. Hay AC, EF và KI đồng quy tại một điểm.
Bài 4. (0,5 điểm) Chứng minh rằng \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
Phương pháp
Dựa vào hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) để chứng minh.
Lời giải
Ta có:
\(\begin{array}{l}9 - {\left( {1 + 4k} \right)^2} = {3^2} - {\left( {1 + 4k} \right)^2} = \left( {3 - 1 - 4k} \right)\left( {3 + 1 + 4k} \right)\\ = \left( {2 - 4k} \right)\left( {4 + 4k} \right) = 2.4\left( {1 - 2k} \right)\left( {1 + k} \right) = 8\left( {1 - 2k} \right)\left( {1 + k} \right) \vdots 8\forall k \in \mathbb{Z}\end{array}\)
Vậy \(9 - {\left( {1 + 4k} \right)^2}\) chia hết cho 8 với mọi số nguyên k.
Đề thi giữa kì 1 Toán 8 - Đề số 2 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức và kỹ năng đã học trong giai đoạn đầu năm học lớp 8. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của toán học.
Thông thường, đề thi giữa kì 1 Toán 8 - Đề số 2 - Kết nối tri thức sẽ có cấu trúc tương tự như sau:
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 8 - Đề số 2 - Kết nối tri thức, học sinh cần:
Bài toán: Giải phương trình: 2x + 5 = 11
Lời giải:
Kết luận: Phương trình có nghiệm x = 3
Để hỗ trợ học sinh ôn tập và luyện thi hiệu quả, giaitoan.edu.vn cung cấp:
Hãy dành thời gian ôn tập và luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải toán. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 8 - Đề số 2 - Kết nối tri thức!