Chào mừng các em học sinh lớp 8 đến với đề thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 9.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong chương trình Toán 8, tập trung vào các chủ đề quan trọng của học kì 2.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Phân thức \(\frac{{x + 1}}{{2x - y}}\) là phân thức nghịch đảo của:
\(\frac{{x + 1}}{{2x}}\).
\(\frac{{x - 1}}{{2x - 1}}\).
\(\frac{{2x - y}}{{x + 1}}\).
\(\frac{{2y - x}}{{x + 1}}\).
Điều kiện xác định của phân thức \(\frac{{x - 3}}{{2 + x}}\) là
\(x \ne 3\).
\(x \ne 2\).
\(x \ne - 2\).
\(x \ne - 3\).
Trong các khẳng định sau, khẳng định sai là
\(\frac{{5{x^2}y}}{{x{y^2}}} = \frac{{5x}}{y}\).
\(\frac{{{x^3} - 8}}{{x - 2}} = {x^2} + 2x + 4\).
\(\frac{{x - 5}}{{2 - x}} = \frac{{5 - x}}{{x - 2}}\).
\(\frac{{3 - x}}{{x + 2}} = \frac{{x - 3}}{{x + 2}}\).
Kết quả của phép tính \(\frac{{x - 1}}{{xy}} + \frac{1}{{yz}} + \frac{1}{{xy}} + \frac{{y - 1}}{{yz}}\) bằng
\(\frac{{x + y}}{{xyz}}\).
\(\frac{{({\rm{x}} - 1)({\rm{y}} - 1)}}{{{{({\rm{xyz}})}^2}}}\).
\(\frac{{({\rm{x}} - 1)({\rm{y}} - 1)}}{{2{\rm{xyz}}}}\).
\(\frac{{y + z}}{{yz}}\).
Tích của hai phân thức \(\frac{{x(x + 3)}}{{5(x - 3)}}\) và \(\frac{{2(x - 3)}}{{{{(x + 3)}^2}}}\) bằng
\(\frac{{2{\rm{x}}}}{5}\).
\(\frac{{2{\rm{x}}}}{{{\rm{x}} + 3}}\).
\(\frac{{2x}}{{5(x + 3)}}\).
\(\frac{{x + 2}}{{5(x + 3)}}\).
Trong đẳng thức \(\frac{{{x^2} + x}}{{4{x^2} - 1}}:\frac{{x + 1}}{{2x - 1}} = \frac{x}{Q}\). Khi đó đa thức Q là
\(2x - 1\).
\(2x\).
\(1 - 2x\).
\(2x + 1\).
Cho $\Delta ABC\backsim \Delta XYZ$ theo tỉ số đồng dạng \(k = 3\). Kết luận nào sau đây đủng?
\(AB = 3XY\).
\(AB = 3YZ\).
\(XY = 3AB\).
\(\,\widehat A = 3\widehat X\).
Cho hình vẽ, biết \(\frac{{AD}}{{BD}} = \frac{{BD}}{{BC}} = \frac{{AB}}{{DC}} = \frac{1}{2}\). Hãy cho biết hai tam giác nào đồng dạng?
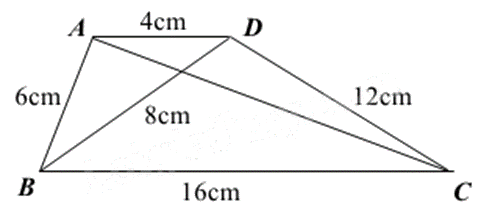
$\Delta ABC\backsim \Delta DBC$.
$\Delta ADB\backsim \Delta DBC$.
$\Delta ABD\backsim \Delta BDC$.
$\Delta ADC\backsim \Delta ABC$.
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây (như hình vẽ). Biết cọc cao 1,5m so với mặt đất, chân cọc cách gốc cây 8m và cách bóng của đỉnh cọc 2m. Khi đó, chiều cao AB của cây là:
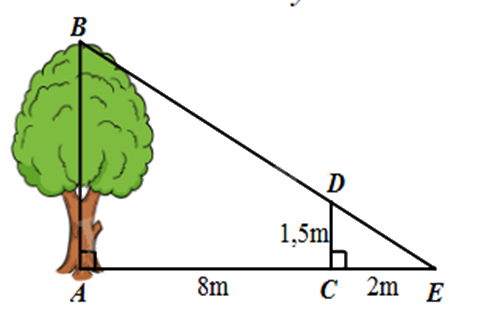
3m.
7,5m.
6m.
13,3m.
Một tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường. Biết chu vi tứ giác đó là \(52\;{\rm{cm}}\) và một đường chéo là \(10\;{\rm{cm}}\). Độ dài đường chéo còn lại là
\(12\;{\rm{cm}}\).
\(18\;{\rm{cm}}\).
\(16\;{\rm{cm}}\).
\(24\;{\rm{cm}}\).
Nếu $\Delta ABC\backsim \Delta MNP$ theo tỉ số đồng dạng là \(k = \frac{2}{5}\) thì $\Delta MNP\backsim \Delta ABC$ theo tỉ số đồng dạng là
\(k' = 2\).
\(k' = 5\).
\(k' = \frac{2}{5}\).
\(k' = \frac{5}{2}\).
Cho các hình sau:

Hình đồng dạng với hình H là
hình 1.
hình 2.
hình 3.
hình 4.
Cho biểu thức \(A = \frac{{8x}}{{4{x^2} - 1}}:\frac{{4x}}{{10x - {\rm{ }}5}}\).
a) Điều kiện xác định của phân thức A là \(x \ne \frac{1}{2}\).
b) Rút gọn biểu thức A ta được kết quả \(\frac{{10}}{{2x + 1}}\).
c) Khi \(x = 2\) thì giá trị của biểu thức \(A = 2\).
d) Các giá trị \(x\) nguyên để A nguyên là \(x \in \left\{ { - 3; - 1;0;2} \right\}\).
Cho hình bình hành ABCD (AB > BC), điểm \(M \in AB\). Đường thẳng DM cắt AC tại K, cắt BC tại N. Cho AB = 10cm, AD = 9cm, AM = 6cm.
a) $\Delta ADK\backsim \Delta CNK$.
b) \(\frac{{KM}}{{KD}} = \frac{{KA}}{{KC}}\).
c) \(K{D^2} = KM.MN\).
d) \(CN = 10cm\).
Tính giá trị của biểu thức \(B = \frac{{x + 1}}{{x - 3}}\) khi \(\left| {x - 2} \right| = 1\).
Đáp án:
Một con thuyền đang neo ở một điểm cách chân tháp hải đăng 180m. Biết tháp hải đăng cao \(25\;{\rm{m}}\). Khoảng cách từ thuyền đến đỉnh tháp hải đăng bằng (làm tròn kết quả đến hàng đơn vị):

Đáp án:
Cho \(\Delta ABC\) vuông tại A có \(AB = 12cm,AC = 16cm\). Đường cao AH. Độ dài đoạn thẳng AH là …cm. (viết dưới dạng số thập phân)
Đáp án:
Giá trị nhỏ nhất của \(D = \frac{6}{{ - {x^2} + 2x - 3}}\) là
Đáp án:
Cho biểu thức \(P = \frac{{{x^2} + 4x + 4}}{{4 - {x^2}}} + \frac{{6x + 8}}{{x - 2}}\) với \(x \ne \pm 2\).
a) Rút gọn biểu thức P.
b) Tính giá trị của biểu thức P tại \(x = 6\).
Cho \(\Delta ABC\) có AB = 9cm, AC = 12cm, BC = 15cm. Trên cạnh AC lấy điểm D sao cho CD = 4cm, trên cạnh BC lấy điểm M sao cho BM = 10cm. Kẻ đoạn thẳng MD.
a) Chứng tỏ rằng DM // AB.
b) Chứng minh $\Delta BAC\backsim \Delta MDC$.
c) Xác định tỉ số giữa diện tích của tam giác MDC với diện tích tam giác ABC.
Cho các số \(x,y,z \ne 0\) thỏa mãn \(x + y + z = xyz\) và \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 3\). Tính giá trị biểu thức \(B = \frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} + \frac{1}{{{z^2}}}\).
Phân thức \(\frac{{x + 1}}{{2x - y}}\) là phân thức nghịch đảo của:
\(\frac{{x + 1}}{{2x}}\).
\(\frac{{x - 1}}{{2x - 1}}\).
\(\frac{{2x - y}}{{x + 1}}\).
\(\frac{{2y - x}}{{x + 1}}\).
Đáp án : C
Hai phân thức nghịch đảo nếu tích của chúng bằng 1.
Vì \(\frac{{x + 1}}{{2x - y}}.\frac{{2x - y}}{{x + 1}} = 1\) nên phân thức nghịch đảo của phân thức \(\frac{{x + 1}}{{2x - y}}\) là \(\frac{{2x - y}}{{x + 1}}\).
Đáp án C
Điều kiện xác định của phân thức \(\frac{{x - 3}}{{2 + x}}\) là
\(x \ne 3\).
\(x \ne 2\).
\(x \ne - 2\).
\(x \ne - 3\).
Đáp án : C
Phân thức \(\frac{A}{B}\) xác định khi \(B \ne 0\).
Điều kiện xác định của phân thức \(\frac{{x - 3}}{{2 + x}}\) là \(2 + x \ne 0\) hay \(x \ne - 2\).
Đáp án C
Trong các khẳng định sau, khẳng định sai là
\(\frac{{5{x^2}y}}{{x{y^2}}} = \frac{{5x}}{y}\).
\(\frac{{{x^3} - 8}}{{x - 2}} = {x^2} + 2x + 4\).
\(\frac{{x - 5}}{{2 - x}} = \frac{{5 - x}}{{x - 2}}\).
\(\frac{{3 - x}}{{x + 2}} = \frac{{x - 3}}{{x + 2}}\).
Đáp án : D
Sử dụng tính chất của phân thức đại số:
\(\frac{A}{B} = \frac{{A.M}}{{B.M}}\) (M là một đa thức khác 0)
\(\frac{A}{B} = \frac{{A:N}}{{B:N}}\) (N là một nhân tử chung)
\(\frac{A}{B} = \frac{{ - A}}{{ - B}}\)
Ta có:
\(\frac{{5{x^2}y}}{{x{y^2}}} = \frac{{5{x^2}y:xy}}{{x{y^2}:xy}} = \frac{{5x}}{y}\) nên A đúng.
\(\frac{{{x^3} - 8}}{{x - 2}} = \frac{{\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)}}{{x - 2}} = {x^2} + 2x + 4\) nên B đúng.
\(\frac{{x - 5}}{{2 - x}} = \frac{{ - \left( {x - 5} \right)}}{{ - \left( {2 - x} \right)}} = \frac{{5 - x}}{{x - 2}}\) nên C đúng.
\(\frac{{3 - x}}{{x + 2}} = \frac{{ - \left( {3 - x} \right)}}{{ - \left( {x + 2} \right)}} = \frac{{x - 3}}{{ - x - 2}} \ne \frac{{x - 3}}{{x + 2}}\) nên D sai.
Đáp án D
Kết quả của phép tính \(\frac{{x - 1}}{{xy}} + \frac{1}{{yz}} + \frac{1}{{xy}} + \frac{{y - 1}}{{yz}}\) bằng
\(\frac{{x + y}}{{xyz}}\).
\(\frac{{({\rm{x}} - 1)({\rm{y}} - 1)}}{{{{({\rm{xyz}})}^2}}}\).
\(\frac{{({\rm{x}} - 1)({\rm{y}} - 1)}}{{2{\rm{xyz}}}}\).
\(\frac{{y + z}}{{yz}}\).
Đáp án : D
Nhóm các phân thức cùng mẫu vào để cộng phân thức cùng mẫu: \(\frac{A}{B} + \frac{C}{B} = \frac{{A + C}}{B}\)
Sau đó cộng các phân thức khác mẫu vừa tính được: \(\frac{A}{B} + \frac{C}{D} = \frac{{AD + BC}}{{BD}}\)
\(\begin{array}{l}\frac{{x - 1}}{{xy}} + \frac{1}{{yz}} + \frac{1}{{xy}} + \frac{{y - 1}}{{yz}}\\ = \left( {\frac{{x - 1}}{{xy}} + \frac{1}{{xy}}} \right) + \left( {\frac{1}{{yz}} + \frac{{y - 1}}{{yz}}} \right)\\ = \frac{{x - 1 + 1}}{{xy}} + \frac{{1 + y - 1}}{{yz}}\\ = \frac{x}{{xy}} + \frac{y}{{yz}}\\ = \frac{1}{y} + \frac{1}{z}\\ = \frac{{y + z}}{{yz}}\end{array}\)
Đáp án D
Tích của hai phân thức \(\frac{{x(x + 3)}}{{5(x - 3)}}\) và \(\frac{{2(x - 3)}}{{{{(x + 3)}^2}}}\) bằng
\(\frac{{2{\rm{x}}}}{5}\).
\(\frac{{2{\rm{x}}}}{{{\rm{x}} + 3}}\).
\(\frac{{2x}}{{5(x + 3)}}\).
\(\frac{{x + 2}}{{5(x + 3)}}\).
Đáp án : C
Sử dụng quy tắc nhân phân thức: \(\frac{A}{B}.\frac{C}{D} = \frac{{AC}}{{BD}}\)
Ta có:
\(\frac{{x(x + 3)}}{{5(x - 3)}}.\frac{{2(x - 3)}}{{{{(x + 3)}^2}}} = \frac{{2x\left( {x + 3} \right)\left( {x - 3} \right)}}{{5\left( {x - 3} \right){{\left( {x + 3} \right)}^2}}} = \frac{{2x}}{{5\left( {x + 3} \right)}}\)
Đáp án C
Trong đẳng thức \(\frac{{{x^2} + x}}{{4{x^2} - 1}}:\frac{{x + 1}}{{2x - 1}} = \frac{x}{Q}\). Khi đó đa thức Q là
\(2x - 1\).
\(2x\).
\(1 - 2x\).
\(2x + 1\).
Đáp án : D
Sử dụng quy tắc chia phân thức để tính vế trái.
Ta có:
\(\begin{array}{l}\frac{{{x^2} + x}}{{4{x^2} - 1}}:\frac{{x + 1}}{{2x - 1}}\\ = \frac{{x\left( {x + 1} \right)}}{{\left( {2x - 1} \right)\left( {2x + 1} \right)}}.\frac{{2x - 1}}{{x + 1}}\\ = \frac{{x\left( {x + 1} \right)\left( {2x - 1} \right)}}{{\left( {2x - 1} \right)\left( {2x + 1} \right)\left( {x + 1} \right)}}\\ = \frac{x}{{2x + 1}} = \frac{x}{Q}\end{array}\)
Suy ra \(Q = 2x + 1\).
Đáp án D
Cho $\Delta ABC\backsim \Delta XYZ$ theo tỉ số đồng dạng \(k = 3\). Kết luận nào sau đây đủng?
\(AB = 3XY\).
\(AB = 3YZ\).
\(XY = 3AB\).
\(\,\widehat A = 3\widehat X\).
Đáp án : A
$\Delta ABC\backsim \Delta A'B'C'$ theo hệ số tỉ lệ k thì \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = k\).
$\Delta ABC\backsim \Delta XYZ$ theo tỉ số đồng dạng \(k = 3\) nên \(\frac{{AB}}{{XY}} = 3\).
Do đó \(AB = 3XY\).
Đáp án A
Cho hình vẽ, biết \(\frac{{AD}}{{BD}} = \frac{{BD}}{{BC}} = \frac{{AB}}{{DC}} = \frac{1}{2}\). Hãy cho biết hai tam giác nào đồng dạng?
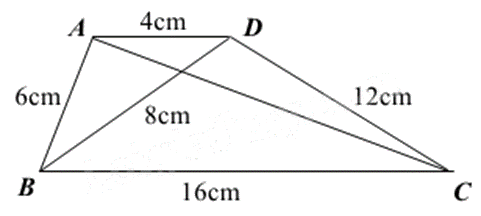
$\Delta ABC\backsim \Delta DBC$.
$\Delta ADB\backsim \Delta DBC$.
$\Delta ABD\backsim \Delta BDC$.
$\Delta ADC\backsim \Delta ABC$.
Đáp án : B
Nếu \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}\) thì $\Delta ABC\backsim \Delta A'B'C'$ (c.c.c).
Vì \(\frac{{AD}}{{BD}} = \frac{{BD}}{{BC}} = \frac{{AB}}{{DC}} = \frac{1}{2}\) nên $\Delta ADB\backsim \Delta DBC\left( c.c.c \right)$,
Đáp án B
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây (như hình vẽ). Biết cọc cao 1,5m so với mặt đất, chân cọc cách gốc cây 8m và cách bóng của đỉnh cọc 2m. Khi đó, chiều cao AB của cây là:
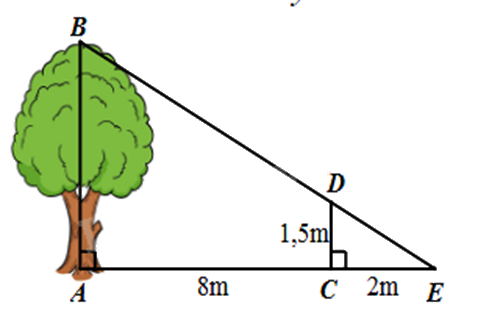
3m.
7,5m.
6m.
13,3m.
Đáp án : B
Sử dụng định lí hai tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của một tam giác là song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Vì cây và cọc cùng vuông góc với mặt đất nên \(DC//AB\).
Do đó $\Delta ABE\backsim \Delta CDE$ (định lí tam giác đồng dạng)
Suy ra \(\frac{{AB}}{{CD}} = \frac{{AE}}{{CE}}\) nên \(AB = \frac{{AE.CD}}{{CE}} = \frac{{\left( {AC + CE} \right).CD}}{{CE}} = \frac{{\left( {8 + 2} \right).1,5}}{2} = 7,5\)
Vậy chiều cao AB của cây là 7,5m.
Đáp án B
Một tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường. Biết chu vi tứ giác đó là \(52\;{\rm{cm}}\) và một đường chéo là \(10\;{\rm{cm}}\). Độ dài đường chéo còn lại là
\(12\;{\rm{cm}}\).
\(18\;{\rm{cm}}\).
\(16\;{\rm{cm}}\).
\(24\;{\rm{cm}}\).
Đáp án : D
Chứng minh tứ giác là hình thoi.
Từ chu vi hình thoi suy ra cạnh = chu vi : 4.
Sử dụng định lí Pythagore để tính đường chéo còn lại.
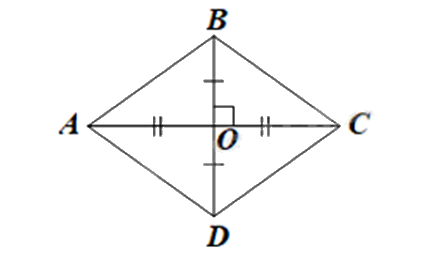
Vì tứ giác ABCD có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường nên ABCD là hình thoi.
Độ dài cạnh của hình thoi ABCD là: \(AB = 52:4 = 13\left( {cm} \right)\)
Giả sử đường chéo \(BD = 10cm\) và O là giao điểm của hai đường chéo thì \(BO = \frac{1}{2}BD = \frac{1}{2}.10 = 5\left( {cm} \right)\)
Áp dụng định lí Pythagore vào tam giác ABO vuông tại O, ta có:
\(A{B^2} = A{O^2} + B{O^2}\) suy ra \(AO = \sqrt {{{13}^2} - {5^2}} = 12\left( {cm} \right)\)
Do O là trung điểm của AC nên \(AC = 2AO = 2.12 = 24\left( {cm} \right)\)
Đáp án D
Nếu $\Delta ABC\backsim \Delta MNP$ theo tỉ số đồng dạng là \(k = \frac{2}{5}\) thì $\Delta MNP\backsim \Delta ABC$ theo tỉ số đồng dạng là
\(k' = 2\).
\(k' = 5\).
\(k' = \frac{2}{5}\).
\(k' = \frac{5}{2}\).
Đáp án : D
Nếu $\Delta ABC\backsim \Delta A'B'C'$ theo tỉ số đồng dạng k thì $\Delta A'B'C'\backsim \Delta ABC$ theo tỉ số đồng dạng \(\frac{1}{k}\).
Nếu $\Delta ABC\backsim \Delta MNP$ theo tỉ số đồng dạng là \(k = \frac{2}{5}\) thì $\Delta MNP\backsim \Delta ABC$ theo tỉ số đồng dạng là \(k' = \frac{5}{2}\).
Đáp án D
Cho các hình sau:

Hình đồng dạng với hình H là
hình 1.
hình 2.
hình 3.
hình 4.
Đáp án : C
Quan sát xem hình nào giống với hình H.
Hình đồng dạng với hình H là hình 3.
Đáp án C
Cho biểu thức \(A = \frac{{8x}}{{4{x^2} - 1}}:\frac{{4x}}{{10x - {\rm{ }}5}}\).
a) Điều kiện xác định của phân thức A là \(x \ne \frac{1}{2}\).
b) Rút gọn biểu thức A ta được kết quả \(\frac{{10}}{{2x + 1}}\).
c) Khi \(x = 2\) thì giá trị của biểu thức \(A = 2\).
d) Các giá trị \(x\) nguyên để A nguyên là \(x \in \left\{ { - 3; - 1;0;2} \right\}\).
a) Điều kiện xác định của phân thức A là \(x \ne \frac{1}{2}\).
b) Rút gọn biểu thức A ta được kết quả \(\frac{{10}}{{2x + 1}}\).
c) Khi \(x = 2\) thì giá trị của biểu thức \(A = 2\).
d) Các giá trị \(x\) nguyên để A nguyên là \(x \in \left\{ { - 3; - 1;0;2} \right\}\).
a) Xác định giá trị của x để mẫu thức khác 0, phân thức chia khác 0.
b) Sử dụng quy tắc chia hai phân thức để rút gọn biểu thức A.
c) Thay \(x = 2\) vào biểu thức A để tính giá trị của A.
d) Để \(A = \frac{k}{{g\left( x \right)}}\,\) nguyên thì \(k \vdots g\left( x \right)\).
Lập bảng để tìm các giá trị của x.
a) Xác định giá trị của x để mẫu thức khác 0, phân thức chia khác 0.
b) Sử dụng quy tắc chia hai phân thức để rút gọn biểu thức A.
c) Thay \(x = 2\) vào biểu thức A để tính giá trị của A.
d) Để \(A = \frac{k}{{g\left( x \right)}}\,\) nguyên thì \(k \vdots g\left( x \right)\).
Lập bảng để tìm các giá trị của x.
a) Sai
Biểu thức A xác định khi:
\(4{x^2} - 1 \ne 0\) và \(10x - 5 \ne 0\) và \(4x \ne 0\) (do \(\frac{{4x}}{{10x - {\rm{ }}5}}\) là phân thức chia)
+) \(4{x^2} - 1 \ne 0\)
\(4{x^2} \ne 1\)
\({x^2} \ne \frac{1}{4}\)
\(x \ne \pm \frac{1}{2}\)
+) \(10x - 5 \ne 0\)
\(10x \ne 5\)
\(x \ne \frac{1}{2}\)
+) \(4x \ne 0\) nên \(x \ne 0\)
Vậy điều kiện xác định của phân thức A là \(x \ne \pm \frac{1}{2}\); \(x \ne 0\).
b) Đúng
Ta có: \(A = \frac{{8x}}{{4{x^2} - 1}}:\frac{{4x}}{{10x - {\rm{ }}5}}\)\(\left( {x \ne \pm \frac{1}{2}} \right)\)
\(\begin{array}{l}A = \frac{{8x}}{{4{x^2} - 1}}.\frac{{10x - {\rm{ }}5}}{{4x}}\\A = \frac{{8x\left( {10x - {\rm{ }}5} \right)}}{{4x\left( {4{x^2} - 1} \right)}}\\A = \frac{{40x\left( {2x - {\rm{ 1}}} \right)}}{{4x\left( {2x - {\rm{ 1}}} \right)\left( {2x + {\rm{ 1}}} \right)}}\\A = \frac{{10}}{{2x + 1}}\end{array}\)
Vậy \(A = \frac{{10}}{{2x + 1}}\).
c) Đúng
Thay \(x = 2\) vào A, ta được:
\(A = \frac{{10}}{{2.2 + 1}} = \frac{{10}}{5} = 2\)
d) Sai
Để A nguyên thì \(\frac{{10}}{{2x + 1}}\) nguyên, khi đó \(10 \vdots \left( {2x + 1} \right)\) hay \(\left( {2x + 1} \right) \in \)Ư(10) = \(\left\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\).
Ta có bảng sau:

Vậy \(x \in \left\{ { - 3; - 1;2} \right\}\) thì A nguyên.
Đáp án: SĐĐS
Cho hình bình hành ABCD (AB > BC), điểm \(M \in AB\). Đường thẳng DM cắt AC tại K, cắt BC tại N. Cho AB = 10cm, AD = 9cm, AM = 6cm.
a) $\Delta ADK\backsim \Delta CNK$.
b) \(\frac{{KM}}{{KD}} = \frac{{KA}}{{KC}}\).
c) \(K{D^2} = KM.MN\).
d) \(CN = 10cm\).
a) $\Delta ADK\backsim \Delta CNK$.
b) \(\frac{{KM}}{{KD}} = \frac{{KA}}{{KC}}\).
c) \(K{D^2} = KM.MN\).
d) \(CN = 10cm\).
a) Chứng minh AD // CN.
Sử dụng định lí tam giác đồng dạng để chứng minh hai tam giác đồng dạng.
b) Chứng minh AM // CD.
Sử dụng định lí tam giác đồng dạng để chứng minh hai tam giác đồng dạng.
Từ đó suy ra tỉ lệ cạnh tương ứng bằng nhau.
c) Đưa các cạnh về tam giác đồng dạng để kiểm tra.
d) Dựa vào tỉ số đồng dạng của hai tam giác để tính NC.
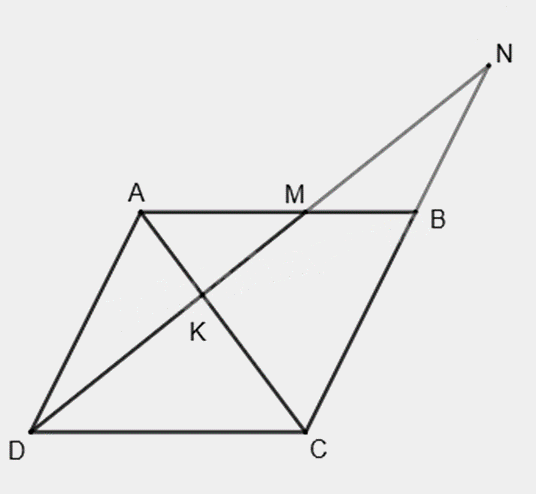
a) Đúng
Vì ABCD là hình bình hành nên AB // CD, AD // BC.
Vì AD // NC (AD // BC) nên $\Delta ADK\backsim \Delta CNK$ (định lí tam giác đồng dạng)
b) Đúng
Vì AM // CD (AB // CD) nên $\Delta AKM\backsim \Delta CKD$ (định lí tam giác đồng dạng)
Suy ra \(\frac{{KM}}{{KD}} = \frac{{KA}}{{KC}}\) (tỉ lệ giữa các cạnh tương ứng) (1)
c) Sai
Từ $\Delta ADK\backsim \Delta CNK$, ta có: \(\frac{{AK}}{{KC}} = \frac{{KD}}{{KN}}\) (2)
Từ (1) và (2) suy ra \(\frac{{KM}}{{KD}} = \frac{{KD}}{{KN}}\) nên \(K{D^2} = KM.KN \ne KM.MN\) nên c sai.
d) Sai
Xét \(\Delta ADM\) và \(\Delta CND\) có:
\(\widehat {AMD} = \widehat {NDC}\) (2 góc so le trong)
\(\widehat {ADM} = \widehat {DNC}\) (2 góc so le trong)
nên $\Delta ADM\backsim \Delta CND\left( g.g \right)$,
Suy ra \(\frac{{AM}}{{AD}} = \frac{{CD}}{{CN}}\).
Vì ABCD là hình bình hành nên CD = AB = 10cm.
Do đó \(CN = \frac{{CD.AD}}{{AM}} = \frac{{10.9}}{6} = 15\left( {cm} \right)\)
Đáp án: ĐĐSS
Tính giá trị của biểu thức \(B = \frac{{x + 1}}{{x - 3}}\) khi \(\left| {x - 2} \right| = 1\).
Đáp án:
Đáp án:
Tính giá trị của x thoả mãn \(\left| {x - 2} \right| = 1\), kiểm tra với điều kiện xác định của B.
Sau đó thay x tìm được vào B.
ĐKXĐ của B là: \(x - 3 \ne 0\) hay \(x \ne 3\).
Ta có: \(\left| {x - 2} \right| = 1\) nên:
\(x - 2 = 1\) hoặc \(x - 2 = - 1\)
\(x = 3\) (L) hoặc \(x = 1\) (TM)
Thay \(x = 1\) vào \(B = \frac{{x + 1}}{{x - 3}}\), ta được:
\(B = \frac{{1 + 1}}{{1 - 3}} = - 1\)
Đáp án: -1
Một con thuyền đang neo ở một điểm cách chân tháp hải đăng 180m. Biết tháp hải đăng cao \(25\;{\rm{m}}\). Khoảng cách từ thuyền đến đỉnh tháp hải đăng bằng (làm tròn kết quả đến hàng đơn vị):

Đáp án:
Đáp án:
Sử dụng định lí Pythagore để tính khoảng cách từ thuyền đến đỉnh tháp hải đăng.
Khoảng cách từ thuyền đến đỉnh tháp hải đăng là: \(\sqrt {{{25}^2} + {{180}^2}} = 182\left( m \right)\)
Đáp án: 182
Cho \(\Delta ABC\) vuông tại A có \(AB = 12cm,AC = 16cm\). Đường cao AH. Độ dài đoạn thẳng AH là …cm. (viết dưới dạng số thập phân)
Đáp án:
Đáp án:
Sử dụng định lí Pythagore vào tam giác ABC để tính BC.
Chứng minh \(\Delta HBA\backsim \Delta ABC\) \(\left( g-g \right)\) suy ra tỉ số của các cạnh tương ứng để tính AH.
Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2}\).
Do đó: \(BC = \sqrt {A{B^2} + A{C^2}} \)
Hay \(BC = \sqrt {{{12}^2} + {{16}^2}} = \sqrt {144 + 256} = \sqrt {400} = 20cm\).
Xét \(\Delta HBA\) và \(\Delta ABC\) có:
\(\widehat {\rm H} = \widehat {\rm A} = 90^\circ \)
\(\widehat {\rm B}\) chung
nên \(\Delta HBA\backsim \Delta ABC\) \(\left( {g - g} \right)\)
Suy ra \(\frac{{AH}}{{AB}} = \frac{{AC}}{{BC}}\) nên \(AH = \frac{{AC.AB}}{{BC}} = \frac{{16.12}}{{20}} = 9,6\left( {cm} \right)\)
Đáp án: 9,6
Giá trị nhỏ nhất của \(D = \frac{6}{{ - {x^2} + 2x - 3}}\) là
Đáp án:
Đáp án:
Để biểu thức \(D = \frac{k}{{f\left( x \right)}}\) đạt giá trị nhỏ nhất thì \(f\left( x \right)\) phải đạt giá trị lớn nhất.
Tìm giá trị lớn nhất của \(f\left( x \right)\) để tính giá trị nhỏ nhất của D.
Ta có: \( - {x^2} + 2x - 3 = - \left( {{x^2} - 2x + 3} \right) = - {\left( {x - 1} \right)^2} - 2 \le - 2\)
Để \(D = \frac{6}{{ - {x^2} + 2x - 3}}\) đạt giá trị nhỏ nhất thì \( - {x^2} + 2x - 3\) đạt giá trị lớn nhất.
Ta có: \( - {x^2} + 2x - 3 = - \left( {{x^2} - 2x + 3} \right) = - {\left( {x - 1} \right)^2} - 2 \le - 2\)
Suy ra giá trị lớn nhất của \( - {x^2} + 2x - 3\) là -2.
Khi đó \(\frac{6}{{ - {x^2} + 2x - 3}} \ge \frac{6}{{ - 2}} = - 3\).
Dấu “=” xảy ra là giá trị nhỏ nhất của \(D = \frac{6}{{ - {x^2} + 2x - 3}}\).
Vậy giá trị nhỏ nhất của D là -3.
Đáp án: -3
Cho biểu thức \(P = \frac{{{x^2} + 4x + 4}}{{4 - {x^2}}} + \frac{{6x + 8}}{{x - 2}}\) với \(x \ne \pm 2\).
a) Rút gọn biểu thức P.
b) Tính giá trị của biểu thức P tại \(x = 6\).
a) Sử dụng quy tắc cộng phân thức khác mẫu để rút gọn P.
b) Kiểm tra xem \(x = 6\) có thoả mãn điều kiện xác định không.
Nếu thoả mãn, thay \(x = 6\) vào P.
a) Với \(x \ne \pm 2\), ta có:
\(\begin{array}{l}P = \frac{{{x^2} + 4x + 4}}{{4 - {x^2}}} + \frac{{6x + 8}}{{x - 2}}\\ = \frac{{{{\left( {x + 2} \right)}^2}}}{{\left( {2 + x} \right)\left( {2 - x} \right)}} + \frac{{6x + 8}}{{x - 2}}\\ = \frac{{x + 2}}{{2 - x}} + \frac{{6x + 8}}{{x - 2}}\\ = \frac{{ - \left( {x + 2} \right)}}{{x - 2}} + \frac{{6x + 8}}{{x - 2}}\\ = \frac{{ - x - 2 + 6x + 8}}{{x - 2}}\\ = \frac{{5x + 6}}{{x - 2}}\end{array}\)
Vậy \(P = \frac{{5x + 6}}{{x - 2}}\)
b) Với \(x = 6\) (TMĐK), thay vào biểu thức \(P = \frac{{5x + 6}}{{x - 2}}\), ta được:
\(P = \frac{{5.6 + 6}}{{6 - 2}} = \frac{{30 + 6}}{4} = \frac{{36}}{4} = 9\)
Vậy \(P = 9\) khi \(x = 6\).
Cho \(\Delta ABC\) có AB = 9cm, AC = 12cm, BC = 15cm. Trên cạnh AC lấy điểm D sao cho CD = 4cm, trên cạnh BC lấy điểm M sao cho BM = 10cm. Kẻ đoạn thẳng MD.
a) Chứng tỏ rằng DM // AB.
b) Chứng minh $\Delta BAC\backsim \Delta MDC$.
c) Xác định tỉ số giữa diện tích của tam giác MDC với diện tích tam giác ABC.
a) Chứng minh \(\frac{{CM}}{{CB}} = \frac{{CD}}{{CA}}\), ta được DM // AB (theo định lí Thalès đảo)
b) Áp dụng định lí tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của một tam giác là song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
c) Áp dụng tỉ số diện tích tương ứng của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng từ đó tính được \(\frac{{{S_{\Delta MDC}}}}{{{S_{\Delta BAC}}}}\).
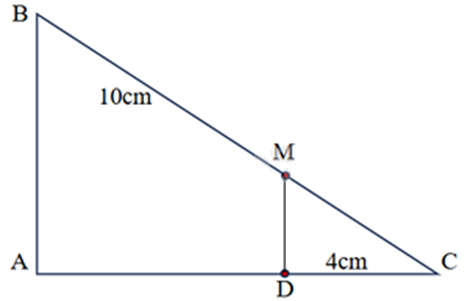
a) Vì M thuộc đoạn BC nên BM + CM = BC
suy ra CM = BC – BM = 15 – 10 = 5 (cm)
Ta có: \(\frac{{CM}}{{CB}} = \frac{5}{{15}} = \frac{1}{3}\) và \(\frac{{CD}}{{CA}} = \frac{4}{{12}} = \frac{1}{3}\) suy ra \(\frac{{CM}}{{CB}} = \frac{{CD}}{{CA}}\) nên DM // AB (theo định lí Thalès đảo)
b) Vì DM // AB nên $\Delta BAC\backsim \Delta MDC$ (định lí tam giác đồng dạng)
c) Vì $\Delta BAC\backsim \Delta MDC$ nên \(\frac{{{S_{\Delta MDC}}}}{{{S_{\Delta BAC}}}} = \frac{{C{D^2}}}{{A{C^2}}} = {\left( {\frac{{CD}}{{AC}}} \right)^2} = {\left( {\frac{4}{{12}}} \right)^2} = {\left( {\frac{1}{3}} \right)^2} = \frac{1}{9}\).
Cho các số \(x,y,z \ne 0\) thỏa mãn \(x + y + z = xyz\) và \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 3\). Tính giá trị biểu thức \(B = \frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} + \frac{1}{{{z^2}}}\).
Từ giả thiết \(x + y + z = xyz\) suy ra \(\frac{1}{{xy}} + \frac{1}{{yz}} + \frac{1}{{zx}} = 1\).
Biến đổi B thành biểu thức chứa \(\frac{1}{{xy}} + \frac{1}{{yz}} + \frac{1}{{zx}}\) và \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z}\).
Khi đó thay số ta tính được B.
Do \(x,y,z \ne 0\) và \(x + y + z = xyz\) nên ta có:
\(\begin{array}{l}x + y + z = xyz\\\frac{{x + y + z}}{{xyz}} = 1\\\frac{x}{{xyz}} + \frac{y}{{xyz}} + \frac{z}{{xyz}} = 1\\\frac{1}{{xy}} + \frac{1}{{yz}} + \frac{1}{{zx}} = 1\end{array}\).
Xét biểu thức:
\(B = \frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} + \frac{1}{{{z^2}}} = {\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)^2} - 2\left( {\frac{1}{{xy}} + \frac{1}{{yz}} + \frac{1}{{zx}}} \right)\)
Khi đó: \(B = {3^2} - 2.1 = 9 - 2 = 7\).
Vậy \(B = 7\).
Đề thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 9 là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong học kì 2. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính như đa thức, phân thức đại số, phương trình bậc nhất một ẩn, hệ phương trình bậc nhất hai ẩn, bất phương trình bậc nhất một ẩn, và các ứng dụng thực tế của đại số.
Thông thường, đề thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 9 có cấu trúc như sau:
Phần này thường yêu cầu học sinh thực hiện các phép toán với đa thức và phân thức, như cộng, trừ, nhân, chia, và rút gọn. Học sinh cần nắm vững các quy tắc về dấu ngoặc, lũy thừa, và các tính chất của phép toán.
Học sinh cần thành thạo các bước giải phương trình bậc nhất một ẩn, bao gồm việc biến đổi phương trình về dạng ax = b, và tìm nghiệm x. Ngoài ra, học sinh cũng cần biết cách kiểm tra nghiệm của phương trình.
Phần này yêu cầu học sinh giải hệ phương trình bằng các phương pháp như phương pháp thế và phương pháp cộng đại số. Học sinh cần hiểu rõ ý nghĩa hình học của hệ phương trình và cách xác định nghiệm của hệ.
Học sinh cần nắm vững các quy tắc giải bất phương trình bậc nhất một ẩn, bao gồm việc biến đổi bất phương trình về dạng ax ≤ b (hoặc ax ≥ b), và tìm tập nghiệm. Học sinh cũng cần biết cách biểu diễn tập nghiệm trên trục số.
Phần này thường yêu cầu học sinh giải các bài toán thực tế liên quan đến các chủ đề đã học, như bài toán về tốc độ, thời gian, quãng đường, hoặc bài toán về lợi nhuận, chi phí.
Để đạt kết quả tốt trong đề thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 9, học sinh cần:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu ôn thi và luyện tập cho học sinh lớp 8, bao gồm:
Hãy dành thời gian ôn tập và luyện tập đầy đủ trước khi bước vào kỳ thi. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 9!