Chào mừng các em học sinh lớp 8 đến với đề thi học kì 2 môn Toán - Đề số 5, chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 2, chuẩn bị tốt nhất cho kỳ thi sắp tới.
Để giải phương trình \(\frac{{2x - 3}}{4} - \frac{{1 - x}}{5} = 1\), một bạn học sinh thực hiện như sau:
Bước 1: \(\frac{{5\left( {2x - 3} \right)}}{{20}} - \frac{{4\left( {1 - x} \right)}}{{20}} = 1\)
Bước 2: \(10x - 15 - 4 + 4x = 1\)
Bước 3: \(14x - 19 = 1\)
Bước 4: \(14x = 20\)
Bước 5. \(x = \frac{{20}}{{14}} = \frac{{10}}{7}\)
Bạn học sinh thực hiện giải như vậy là:
Phương trình nào sau đây không có tập nghiệm là \(S = \left\{ 3 \right\}\)?
Cho đường thẳng d là đồ thị của hàm số \(y = 3x - \frac{1}{2}\). Giao điểm của d với trục tung là điểm nào sau đây?
Cho đường thẳng \(d:y = mx - 5\) đi qua điểm \(A\left( { - 1;2} \right)\). Hệ số góc của đường thẳng d là:
Một hộp có 5 quả bóng màu đỏ và 3 quả bóng màu xanh. Nếu bạn lấy ngẫu nhiên một quả bóng từ hộp, xác suất để lấy được quả bóng màu đỏ là bao nhiêu?
Trong trận chung kết bóng đá World Cup năm 2022 giữa hai đội Argentina và Pháp, để dự đoán kết quả, người ta bỏ cùng loại thức ăn vào hai hộp giống nhau, một hộp có gắn cờ Argentina, một hộp gắn cờ Pháp và cho Paul chọn hộp thức ăn. Người ta cho rằng nếu Paul chọn hộp gắn cờ nước nào thì đội bóng của nước đó thắng. Paul chọn ngẫu nhiên một hộp. Tính xác suất để Paul dự đoán đội Pháp thắng.
Hình chóp tam giác đều và hình chóp tứ giác đều có các mặt bên là các hình gì?
Một khúc gỗ trang trí có dạng hình chóp tam giác đều. Biết diện tích đáy của khúc gỗ bằng \(42c{m^2}\), thể tích của khúc gỗ bằng \(84c{m^3}\), chiều cao của khúc gỗ bằng:
Cho hình vẽ sau, chọn câu trả lời đúng.
Cho hình vẽ sau, tỉ số \(\frac{{BE}}{{CE}}\) bằng
Cho các khẳng định sau:
(1) Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh.
(2) Hai hình tam giác cân bất kì luôn đồng dạng với nhau.
(3) Hai hình thoi bất kì luôn đồng dạng với nhau.
Số khẳng định đúng là:
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
1. Giải các phương trình sau:
a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)
2. Cho hai hàm số \(d:y = x + 3\) và \(d':y = \left( {m - 2} \right)x + 1\) (m là tham số).
a) Với giá trị nào của m thì đồ thị hàm số d’ đi qua điểm \(M\left( {3; - 2} \right)\)
b) Với giá trị nào của m thì đồ thị hàm số trên là hai đường thẳng cắt nhau.
Giải bài toán bằng cách lập phương trình
Trong hội thi STEM của một trường trung học cơ sở, ban tổ chức đưa ra quy tắc chấm thi cho bài thi gồm 25 câu hỏi như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được 6 điểm, nếu trả lời không đúng thì không được điểm, nếu không trả lời thì được 1 điểm. Một học sinh làm bài thi và có số câu trả lời đúng gấp 2 lần số câu trả lời không đúng, kết quả đạt 79 điểm. Hỏi bài thi của học sinh đó có bao nhiêu câu trả lời đúng? Bao nhiêu câu trả lời không đúng? Bao nhiêu câu không trả lời?
1. Thả một vật dụng không thấm nước hình chóp tứ giác đều như hình bên vào một chiếc bình đang chứa 780 ml nước. Hỏi nước có tràn ra khỏi bình không, biết rằng vật chìm hẳn xuống nước và dung tích của bình là \(1000ml\).
2. Cho \(\Delta ABC\) có \(AB = 2cm,AC = 4cm\). Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\).
a) Chứng minh $\Delta ABD\backsim \Delta ACB$
b) Tính AD và DC.
c) Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\). Chứng minh rằng diện tích \(\Delta ABH\) gấp 4 lần diện tích \(\Delta ADE\).
Hai ban An và Bình chơi 1 ván oẳn tù tì gồm 12 lần theo luật chơi: Búa (B) thắng Kéo (K), Kéo (K) thẳng Lá (L), Lá (L) thẳng Búa (B) và hòa nhau nếu cùng loại. Sau đây là kết quả của mỗi ván chơi:

Tính xác suất thực nghiệm của biến cố “An không thắng Bình”.
Giải phương trình \(\frac{{x - 15}}{{17}} + \frac{{x - 36}}{{16}} + \frac{{x - 58}}{{14}} + \frac{{x - 76}}{{12}} = 14\).
Để giải phương trình \(\frac{{2x - 3}}{4} - \frac{{1 - x}}{5} = 1\), một bạn học sinh thực hiện như sau:
Bước 1: \(\frac{{5\left( {2x - 3} \right)}}{{20}} - \frac{{4\left( {1 - x} \right)}}{{20}} = 1\)
Bước 2: \(10x - 15 - 4 + 4x = 1\)
Bước 3: \(14x - 19 = 1\)
Bước 4: \(14x = 20\)
Bước 5. \(x = \frac{{20}}{{14}} = \frac{{10}}{7}\)
Bạn học sinh thực hiện giải như vậy là:
Đáp án : B
Dựa vào cách giải phương trình bậc nhất một ẩn để kiểm tra.
Bạn học sinh đã thực hiện sai từ bước 1, vì muốn khử mẫu thì cần quy đồng cả hai vế của phương trình mà bạn chỉ quy đồng vế trái.
Đáp án B.
Phương trình nào sau đây không có tập nghiệm là \(S = \left\{ 3 \right\}\)?
Đáp án : B
Giải các phương trình trên để xác định.
\(\begin{array}{l}3x - 9 = 0\\3x = 9\\x = 3\end{array}\)
suy ra tập nghiệm của phương trình A là \(S = \left\{ 3 \right\}\).
\(\begin{array}{l}2x + 6 = 0\\2x = - 6\\x = - 3\end{array}\)
suy ra tập nghiệm của phương trình B là \(S = \left\{ { - 3} \right\}\).
\(\begin{array}{l}2\left( {x - 1} \right) - \left( {3x - 5} \right) = 6 - 2x\\2x - 2 - 3x + 5 = 6 - 2x\\2x - 3x + 2x = 6 + 2 - 5\\x = 3\end{array}\)
suy ra tập nghiệm của phương trình C là \(S = \left\{ 3 \right\}\).
\(\frac{{x - 1}}{2} - 1 = 0\)
\(\begin{array}{l}\frac{{x - 1}}{2} - \frac{2}{2} = 0\\x - 1 - 2 = 0\\x = 3\end{array}\)
suy ra tập nghiệm của phương trình D là \(S = \left\{ 3 \right\}\).
Đáp án B.
Cho đường thẳng d là đồ thị của hàm số \(y = 3x - \frac{1}{2}\). Giao điểm của d với trục tung là điểm nào sau đây?
Đáp án : D
Giao điểm của đồ thị hàm số với trục tung là điểm có hoành độ bằng 0.
Tung độ giao điểm của d với trục tung là: \(y = 3.0 - \frac{1}{2} = - \frac{1}{2}\)
Vậy giao điểm của d với trục tung là điểm \(Q\left( {0;\frac{{ - 1}}{2}} \right)\).
Đáp án D.
Cho đường thẳng \(d:y = mx - 5\) đi qua điểm \(A\left( { - 1;2} \right)\). Hệ số góc của đường thẳng d là:
Đáp án : C
Thay tọa độ điểm A vào phương trình đường thẳng d để tìm m.
Vì đường thẳng \(d:y = mx - 5\) đi qua điểm \(A\left( { - 1;2} \right)\) nên ta có:
\(\begin{array}{l}2 = m.\left( { - 1} \right) - 5\\m = - 5 - 2\\m = - 7\end{array}\)
Đáp án C.
Một hộp có 5 quả bóng màu đỏ và 3 quả bóng màu xanh. Nếu bạn lấy ngẫu nhiên một quả bóng từ hộp, xác suất để lấy được quả bóng màu đỏ là bao nhiêu?
Đáp án : A
Xác suất lấy được quả bóng đỏ bằng tỉ số giữa số quả bóng đỏ với tổng số quả bóng.
Có tất cả 5 + 3 = 8 quả bóng trong hộp.
Xác suất để lấy được quả bóng màu đỏ là: \(\frac{5}{8}\).
Đáp án A.
Trong trận chung kết bóng đá World Cup năm 2022 giữa hai đội Argentina và Pháp, để dự đoán kết quả, người ta bỏ cùng loại thức ăn vào hai hộp giống nhau, một hộp có gắn cờ Argentina, một hộp gắn cờ Pháp và cho Paul chọn hộp thức ăn. Người ta cho rằng nếu Paul chọn hộp gắn cờ nước nào thì đội bóng của nước đó thắng. Paul chọn ngẫu nhiên một hộp. Tính xác suất để Paul dự đoán đội Pháp thắng.
Đáp án : B
Dựa vào kiến thức về xác suất.
Vì việc Paul dự đoán đội Argentina hay Pháp thắng là hai biến cố đồng khả năng nên xác suất để Paul dự đoán đội Pháp thắng là \(\frac{1}{2}\).
Đáp án B.
Hình chóp tam giác đều và hình chóp tứ giác đều có các mặt bên là các hình gì?
Đáp án : B
Dựa vào đặc điểm của hình chóp tam giác đều và hình chóp tứ giác đều.
Hình chóp tam giác đều và hình chóp tứ giác đều có các mặt bên là hình tam giác cân.
Đáp án B.
Một khúc gỗ trang trí có dạng hình chóp tam giác đều. Biết diện tích đáy của khúc gỗ bằng \(42c{m^2}\), thể tích của khúc gỗ bằng \(84c{m^3}\), chiều cao của khúc gỗ bằng:
Đáp án : C
Dựa vào công thức tính thể tích hình chóp tam giác đều suy ra chiều cao của khúc gỗ.
Ta có công thức tính thể tích hình chóp tam giác đều là:
\(V = \frac{1}{3}h.S \Rightarrow h = \frac{{3V}}{S}\)
Chiều cao của khúc gỗ là:
\(h = \frac{{3V}}{S} = \frac{{3.84}}{{42}} = 6\left( {cm} \right)\)
Đáp án C.
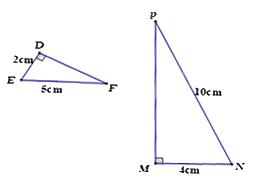
Cho hình vẽ sau, chọn câu trả lời đúng.
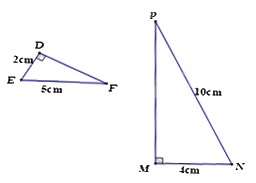
Đáp án : C
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.
Xét \(\Delta DEF\) và \(\Delta MNP\) có:
\(\begin{array}{l}\widehat D = \widehat M = {90^0}\\\frac{{DE}}{{MN}} = \frac{{EF}}{{NP}}\left( {\frac{2}{4} = \frac{5}{{10}} = \frac{1}{2}} \right)\end{array}\)
nên $\Delta DEF\backsim \Delta MNP$ (cạnh huyền – cạnh góc vuông)
Đáp án C.
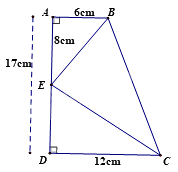
Cho hình vẽ sau, tỉ số \(\frac{{BE}}{{CE}}\) bằng
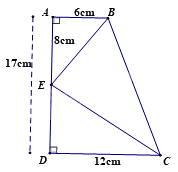
Đáp án : B
Dựa vào kiến thức về hai tam giác vuông đồng dạng để tìm tỉ số.
DE = AD – AE = 17 – 8 = 9(cm)
Xét \(\Delta ABE\) và \(\Delta DEC\) có:
\(\widehat A = \widehat D = {90^0}\)
\(\frac{{AB}}{{DE}} = \frac{{AE}}{{DC}}\left( {\frac{6}{9} = \frac{8}{{12}}\left( { = \frac{2}{3}} \right)} \right)\)
Suy ra $\Delta ABE\backsim \Delta DEC$ (hai cạnh góc vuông) suy ra \(\frac{{BE}}{{CE}} = \frac{{AB}}{{DE}} = \frac{2}{3}\)
Đáp án B.
Cho các khẳng định sau:
(1) Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh.
(2) Hai hình tam giác cân bất kì luôn đồng dạng với nhau.
(3) Hai hình thoi bất kì luôn đồng dạng với nhau.
Số khẳng định đúng là:
Đáp án : B
Dựa vào đặc điểm của các hình để xác định.
Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh nên khẳng định (1) đúng.
Hai tam giác cân bất kì luôn đồng dạng là sai vì các góc trong hai tam giác cân có thể khác nhau.
Hai hình thoi bất kì luôn đồng dạng là sai vì các góc trong hai hình thoi có thể khác nhau.
Đáp án B.
Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Đáp án : D
Dựa vào bán kính hai đường tròn.
Đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng là: \(\frac{6}{3} = 2\).
Đáp án D.
1. Giải các phương trình sau:
a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)
2. Cho hai hàm số \(d:y = x + 3\) và \(d':y = \left( {m - 2} \right)x + 1\) (m là tham số).
a) Với giá trị nào của m thì đồ thị hàm số d’ đi qua điểm \(M\left( {3; - 2} \right)\)
b) Với giá trị nào của m thì đồ thị hàm số trên là hai đường thẳng cắt nhau.
1. Đưa phương trình về dạng \(ax + b = 0\) để giải.
2. a) Thay tọa độ điểm \(M\left( {3; - 2} \right)\) vào hàm số để tìm m.
b) Hai đường thẳng cắt nhau nếu hệ số góc của chúng không bằng nhau.
1. a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
\(\begin{array}{l}7 - 2x - 4 = - x - 4\\ - 2x + x = - 4 - 7 + 4\\ - x = - 7\\x = 7\end{array}\)
Vậy \(x = 7\)z
b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)
\(\begin{array}{l}\frac{{1 - 3x}}{6} + \frac{{6\left( {x - 1} \right)}}{6} = \frac{{3\left( {x + 2} \right)}}{6}\\1 - 3x + 6x - 6 = 3x + 6\\ - 3x + 6x - 3x = 6 + 6 - 1\end{array}\)
\(0 = 11\) (vô lý)
Vậy phương trình vô nghiệm.
2. a) Đồ thị hàm số d’ đi qua điểm \(M\left( {3; - 2} \right)\) nên ta có:
\(\begin{array}{l} - 2 = \left( {m - 2} \right).3 + 1\\ - 2 = 3m - 6 + 1\\3m = - 2 + 6 - 1\\3m = 3\\m = 1\end{array}\)
Vậy với m = 1 thì đồ thị hàm số d’ đi qua điểm \(M\left( {3; - 2} \right)\)
b) Để hàm số \(d:y = x + 3\) và \(d':y = \left( {m - 2} \right)x + 1\) cắt nhau thì:
\(1 \ne m – 2\)
\(m \ne 3\)
Vậy với \(m \ne 3\) thì hàm số \(d:y = x + 3\) và \(d':y = \left( {m - 2} \right)x + 1\) cắt nhau.
Giải bài toán bằng cách lập phương trình
Trong hội thi STEM của một trường trung học cơ sở, ban tổ chức đưa ra quy tắc chấm thi cho bài thi gồm 25 câu hỏi như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được 6 điểm, nếu trả lời không đúng thì không được điểm, nếu không trả lời thì được 1 điểm. Một học sinh làm bài thi và có số câu trả lời đúng gấp 2 lần số câu trả lời không đúng, kết quả đạt 79 điểm. Hỏi bài thi của học sinh đó có bao nhiêu câu trả lời đúng? Bao nhiêu câu trả lời không đúng? Bao nhiêu câu không trả lời?
Giải bài toán bằng cách lập phương trình.
Gọi số câu trả lời không đúng là x \(\left( {x \in N*,x \le 25} \right)\)
Biểu diễn số câu trả lời đúng, số câu không trả lời theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi số câu trả lời không đúng là x \(\left( {x \in N*,x \le 25} \right)\).
Vì số câu trả lời đúng gấp 2 lần số câu trả lời không đúng nên số câu trả lời đúng là \(2x\).
Số câu không trả lời là: \(25 - x - 2x = 25 - 3x\).
Vì học sinh có kết quả đạt 79 điểm nên ta có phương trình:
\(\begin{array}{l}6.2x + 1.\left( {25 - 3x} \right) + 0.x = 79\\12x + 25 - 3x = 79\\9x = 54\\x = 6\left( {TM} \right)\end{array}\)
Khi đó số câu trả lời đúng là: \(2.6 = 12\)(câu)
Số câu không trả lời là: \(25 - 3.6 = 7\)(câu)
Vậy học sinh đó trả lời đúng 12 câu, trả lời không đúng 6 câu và không trả lời 7 câu.
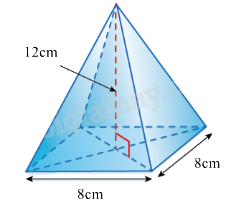
1. Thả một vật dụng không thấm nước hình chóp tứ giác đều như hình bên vào một chiếc bình đang chứa 780 ml nước. Hỏi nước có tràn ra khỏi bình không, biết rằng vật chìm hẳn xuống nước và dung tích của bình là \(1000ml\).
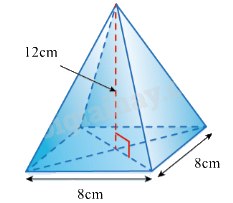
2. Cho \(\Delta ABC\) có \(AB = 2cm,AC = 4cm\). Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\).
a) Chứng minh $\Delta ABD\backsim \Delta ACB$
b) Tính AD và DC.
c) Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\). Chứng minh rằng diện tích \(\Delta ABH\) gấp 4 lần diện tích \(\Delta ADE\).
1. Để xác định xem nước có tràn ra khỏi bình hay không, ta cần tính dung tích của vật dụng hình chóp tứ giác đều.
2. a) Chứng minh $\Delta ABD\backsim \Delta ACB$ theo trường hợp góc – góc.
b) Từ $\Delta ABD\backsim \Delta ACB$ suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra \(A{B^2} = AC.AD\), từ đó ta tính AD và DC.
c) Chứng minh $\Delta ADE\backsim \Delta ABH$ theo trường hợp góc – góc suy ra tỉ số đồng dạng giữa các cặp cạnh tương ứng để chứng minh.
Sử dụng công thức tính diện tích tam giác vuông chứng minh.
1. Thể tích của vật dụng hình chóp tứ giác đều là:
\(V = \frac{1}{3}{.12.8^2} = 256\left( {c{m^3}} \right)\)
Mà \(256c{m^3} = 256ml\)
Sau khi thả vật dụng đó vào chiếc bình thì lượng nước dâng lên thành \(780 + 256 = 1036\left( {ml} \right) > 1000ml\).
Vậy khi thả vật vào bình thì nước sẽ bị tràn.
2.
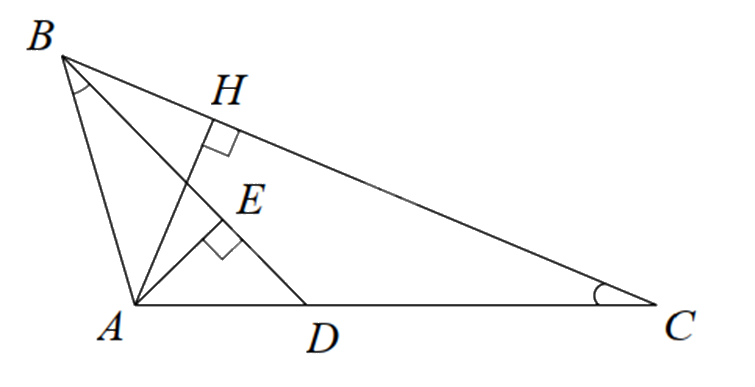
a) Xét \(\Delta ABD\) và \(\Delta ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (gt)
\(\widehat {BAC}\) chung
Suy ra $\Delta ABD\backsim \Delta ACB$ (g.g). (đpcm)
b) Vì $\Delta ABD\backsim \Delta ACB$ (cmt) suy ra \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) nên \(A{B^2} = AC.AD\).
Suy ra \({2^2} = 4.AD\) hay \(AD = 1\left( {cm} \right)\).
Suy ra \(CD = AC - AD = 4 - 1 = 3\left( {cm} \right)\)
c) Do $\Delta ABD\backsim \Delta ACB$ suy ra \(\widehat {ADE} = \widehat {ABC}\).
Xét \(\Delta AED\) và \(\Delta AHB\) có:
\(\widehat E = \widehat H = {90^0}\)
\(\widehat {ADE} = \widehat {ABC}\)(cmt)
Suy ra $\Delta ADE\backsim \Delta ABH\left( g.g \right)$ suy ra \(\frac{{AE}}{{AH}} = \frac{{DE}}{{BH}} = \frac{{AD}}{{AB}} = \frac{1}{2}\).
Do đó \(BH = 2DE;AH = 2AE\).
Từ đó suy ra \({S_{\Delta ABH}} = \frac{1}{2}BH.AH = \frac{1}{2}\left( {2DE} \right)\left( {2AE} \right) = 4.\frac{1}{2}DE.AE = 4{S_{\Delta ADE}}\) (đpcm).
Hai ban An và Bình chơi 1 ván oẳn tù tì gồm 12 lần theo luật chơi: Búa (B) thắng Kéo (K), Kéo (K) thẳng Lá (L), Lá (L) thẳng Búa (B) và hòa nhau nếu cùng loại. Sau đây là kết quả của mỗi ván chơi:

Tính xác suất thực nghiệm của biến cố “An không thắng Bình”.
Tính số lần An không thắng Bình.
Xác suất thực nghiệm của biến cố bằng tỉ số giữa tổng số lần biến cố xuất hiện với tổng số lần thực hiện biến cố.
Quan sát bảng kết quả ta thấy số lần An thắng Bình là 6 lần.
Do đó số lần An không thắng Bình là: 12 – 6 = 6 (lần)
Vậy xác suất thực nghiệm của biến cố “An không thắng Bình” là: \(\frac{6}{{12}} = \frac{1}{2}\).
Giải phương trình \(\frac{{x - 15}}{{17}} + \frac{{x - 36}}{{16}} + \frac{{x - 58}}{{14}} + \frac{{x - 76}}{{12}} = 14\).
Trừ các 2 vế cho 14 theo cách sau:
\(\left( {\frac{{x - 15}}{{17}} - 5} \right) + \left( {\frac{{x - 36}}{{16}} - 4} \right) + \left( {\frac{{x - 58}}{{14}} - 3} \right) + \left( {\frac{{x - 76}}{{12}} - 2} \right) = 0\)
Rút gọn vế trái để giải phương trình.
Trừ các 2 vế cho 14 ta được:
\(\left( {\frac{{x - 15}}{{17}} - 5} \right) + \left( {\frac{{x - 36}}{{16}} - 4} \right) + \left( {\frac{{x - 58}}{{14}} - 3} \right) + \left( {\frac{{x - 76}}{{12}} - 2} \right) = 0\)
\(\begin{array}{l}\frac{{x - 100}}{{17}} + \frac{{x - 100}}{{16}} + \frac{{x - 100}}{{14}} + \frac{{x - 100}}{{12}} = 0\\\left( {x - 100} \right)\left( {\frac{1}{{17}} + \frac{1}{{16}} + \frac{1}{{14}} + \frac{1}{{12}}} \right) = 0\\x - 100 = 0\\x = 0 + 100\\x = 100\end{array}\)
Vậy \(x = 100\)
Kỳ thi học kì 2 Toán 8 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một học kỳ rèn luyện kiến thức. Đề thi học kì 2 Toán 8 - Đề số 5 - Kết nối tri thức là một trong những đề thi được nhiều trường học lựa chọn để đánh giá học sinh. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết để giúp các em học sinh ôn tập hiệu quả.
Đề thi học kì 2 Toán 8 - Đề số 5 - Kết nối tri thức thường bao gồm các phần sau:
Để chuẩn bị tốt nhất cho kỳ thi, các em cần nắm vững các dạng bài tập thường gặp sau:
Dưới đây là hướng dẫn giải chi tiết một số bài tập thường gặp trong đề thi học kì 2 Toán 8 - Đề số 5 - Kết nối tri thức:
Giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Giải:
3x - 1 < 5
3x < 6
x < 2
x + y = 5
2x - y = 1
Giải:
Cộng hai phương trình, ta được:
3x = 6
x = 2
Thay x = 2 vào phương trình x + y = 5, ta được:
2 + y = 5
y = 3
Vậy nghiệm của hệ phương trình là (x, y) = (2, 3)
Đề thi học kì 2 Toán 8 - Đề số 5 - Kết nối tri thức là một cơ hội để các em học sinh thể hiện kiến thức và kỹ năng đã học trong học kì. Hy vọng với những thông tin và hướng dẫn giải chi tiết trong bài viết này, các em sẽ tự tin hơn khi bước vào kỳ thi và đạt được kết quả tốt nhất.