Chào mừng các em học sinh lớp 6 đến với đề thi giữa kì 2 môn Toán, chương trình Chân trời sáng tạo - Đề số 1. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn giữa kì.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học và kiểm tra kết quả một cách hiệu quả. Chúc các em làm bài tốt!
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1. B | 2. A | 3. B | 4. C |
Câu 1
Phương pháp:
Đưa về hai phân số cùng mẫu và so sánh hai phân số bằng nhau hoặc nhân chéo.
Cách giải:
Cách 1:
\(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\)
\(\begin{array}{l}\dfrac{{3x}}{{12}} = \dfrac{{ - 6}}{{12}}\\3x = - 6\\x = - 2\end{array}\)
Cách 2:
\(\begin{array}{l}\dfrac{x}{4} = \dfrac{6}{{ - 12}}\\x = \dfrac{{4.6}}{{ - 12}}\\x = - 2\end{array}\)
Chọn B.
Câu 2
Phương pháp:
Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O.
Cách giải:
Hình trên có 6 tia: Ax, Ay, Bx, By, Cx, Cy.
Chọn A.
Câu 3
Phương pháp:
Sử dụng lý thuyết trục đối xứng của một hình.
Cách giải:
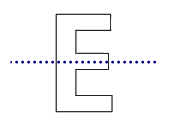
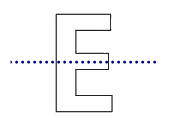
Chữ E có 1 trục đối xứng.
Chọn B.
Câu 4
Phương pháp:
- Số thập phân dương luôn lớn hơn số thập phân âm
- Trong hai số thập phân âm, số nào có số đối lớn hơn thì số đó nhỏ hơn
Cách giải:
Vì \(2,32 > 0,34\) nên \( - 2,32 < - 0,34\)
Do đó, \( - 2,31 < - \,0,34 < 1,2 < 1,41\) nên thứ tự giảm dần của các số là: \(1,41;\,\,\,\,1,2;\,\,\,\,\, - 0,34;\,\,\,\,\, - 2,31.\)
Chọn C.
Phần II: Tự luận
Bài 1
Phương pháp
a) Cộng hai phân số cùng mẫu.
b) Nhóm thích hợp các phân số cùng mẫu.
c) Sử dụng tính chất phân phối của phép nhân và phép cộng.
Cách giải:
a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\)
\(\begin{array}{l} = \dfrac{{ - 7 + 3}}{{16}}\\ = \dfrac{{ - 4}}{{16}}\\ = \dfrac{{ - 1}}{4}\end{array}\)
b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\)
\(\begin{array}{l} = \left( {\dfrac{1}{7} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}} \right) + \dfrac{{ - 1}}{3}\\ = \dfrac{{1 + 10 - 4}}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{7}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{3}{3} + \dfrac{{ - 1}}{3}\\ = \dfrac{{3 - 1}}{3}\\ = \dfrac{2}{3}\end{array}\)
c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
\(\begin{array}{l} = \dfrac{4}{9}.\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{ - 45}}{{26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}.\dfrac{{ - 7 - 45}}{{26}} + \dfrac{1}{3}\\ = \dfrac{4}{9}.\left( { - 2} \right) + \dfrac{1}{3}\\ = \dfrac{{ - 8}}{9} + \dfrac{3}{9}\\ = \dfrac{{ - 8 + 3}}{9}\\ = \dfrac{{ - 5}}{9}\end{array}\)
Bài 2
Phương pháp
Chuyển vế để tìm được \(x\).
Sử dụng phép tính giá trị lũy thừa của một số.
Cách giải:
a) \(x - \frac{{ - 1}}{5} = 1\)
\(\begin{array}{l}\frac{1}{2}x - \frac{{ - 1}}{5} = \frac{3}{2}\\x = \frac{3}{2} + \frac{{ - 1}}{5}\\x = \frac{{13}}{{10}}\end{array}\)
Vậy \(x = \frac{{13}}{{10}}\)
b) \( - \frac{1}{2} + \left( {x - \frac{5}{{11}}} \right) = \frac{{ - 3}}{4}\)
\(\begin{array}{l}x - \frac{5}{{11}} = \frac{{ - 3}}{4} + \frac{1}{2}\\x - \frac{5}{{11}} = \frac{{ - 1}}{4}\\x = \frac{{ - 1}}{4} + \frac{5}{{11}}\\x = \frac{9}{{44}}\end{array}\)
Vậy \(x = \frac{9}{{44}}\)
c) \(\frac{3}{4} + \left( {\frac{2}{5} - x} \right) = \frac{1}{4}\)
\(\frac{2}{5} - x = \frac{1}{4} - \frac{3}{4}\)
\(\frac{2}{5} - x = {\rm{\;}} - \frac{1}{2}\)
\(x = \frac{2}{5} + \frac{1}{2}\)
\(x = \frac{9}{{10}}\)
Vậy \(x = \frac{9}{{10}}\)
Bài 3
Phương pháp
So sánh số học sinh lớp 6A1 với tổng số học sinh khối 6.
So sánh số học sinh lớp 6A4 với tổng số học sinh khối 6.
Tính số học sinh khối 6, từ đó tính số học sinh mỗi lớp 6A1, 6A2, 6A3.
Cách giải:
Vì số học sinh lớp 6A1 bằng \(\dfrac{2}{7}\) tổng số học sinh 3 lớp còn lại => Số học sinh lớp 6A1 bằng \(\dfrac{2}{9}\) tổng số học sinh khối 6.
Số học sinh lớp 6A4 bằng \(1 - \dfrac{2}{9} - \dfrac{{11}}{{45}} - \dfrac{7}{{27}} = \dfrac{{37}}{{135}}\) (tổng số học sinh khối 6)
Số học sinh khối 6 là: \(37:\dfrac{{37}}{{135}} = 135\) (học sinh).
Số học sinh lớp 6A1 là: \(135.\dfrac{2}{9} = 30\) (học sinh).
Số học sinh lớp 6A2 là: \(135.\dfrac{{11}}{{45}} = 33\) (học sinh).
Số học sinh lớp 6A3 là: \(135.\dfrac{7}{{27}} = 35\) (học sinh).
Vậy lớp 6A1 có 30 học sinh, lớp 6A2 có 33 học sinh, lớp 6A3 có 35 học sinh.
Bài 4
Phương pháp
a) Chứng minh K nằm giữa A và Q và suy ra AK + KQ = AQ.
b) Chứng minh A nằm giữa C và K. Tính CK = AC + AK.
Chỉ ra A nằm giữa C, K và AC = AK. Từ đó suy ra A là trung điểm của CK.
c) Tính BA.
Chứng minh A nằm giữa B và K. Tính BK = BA + AK.
So sánh BK và AQ.
Cách giải:
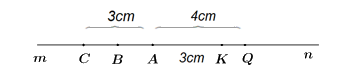
a) Vì AK < AQ (3cm < 4cm) nên K nằm giữa A và Q.
=> AK + KQ = AQ
=> 3 + KQ = 4
=> KQ = 4 – 3
=> KQ = 1 (cm)
b) Vì C và K nằm trên hai tia đối An và Am nên A nằm giữa C và K.
=> CK = AC + AK
=> CK = 3 + 3
=> CK = 6 (cm)
Ta có: A nằm giữa C và K.
AC = AK = 3cm.
=> A là trung điểm của CK.
c) Vì B là trung điểm của AC nên BA = AC : 2 = 3 : 2 = 1,5 (cm).
Vì B, K nằm trên hai tia đối nhau An và Am nên A nằm giữa B và K.
=> BK = BA + AK
=> BK = 1,5 + 3
=> BK = 4,5 (cm)
Mà AQ = 4 (cm)
=> BK > AQ.
Bài 5
Phương pháp
Nhận xét:
\(\dfrac{1}{{1.2}} = 1 - \dfrac{1}{2};\) \(\dfrac{1}{{2.3}} = \dfrac{1}{2} - \dfrac{1}{3};\)\(\dfrac{1}{{3.4}} = \dfrac{1}{3} - \dfrac{1}{4};\)…; \(\dfrac{1}{{2011.2012}} = \dfrac{1}{{2011}} - \dfrac{1}{{2012}}\) sau đó rút gọn các cặp phân số đối nhau rồi thực hiện tính.
Cách giải:
\(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\)
\( = 7.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \ldots + \dfrac{1}{{2011.2012}}} \right)\)
\( = 7.\left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + \ldots + \dfrac{1}{{2011}} - \dfrac{1}{{2012}}} \right)\)
\( = 7.\left( {1 - \dfrac{1}{{2012}}} \right) = \dfrac{{14077}}{{2012}}\)
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Giá trị của x trong biểu thức \(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\) là:
A. -8
B. -2
C. 8
D. 2
Câu 2:Hình bên có mấy tia:
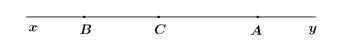
A. 6
B. 3
C. 4
D. 8
Câu 3: Chữ E có bao nhiêu trục đối xứng?
A. \(0\)
B. \(1\)
C. \(2\)
D. \(3\)
Câu 4:Sắp xếp các số \(1,2;\,\,\,\, - 0,34;\,\,\,\, - 2,31;\,\,\,\,1,41\) theo thứ tự giảm dần:
A. \(1,2;\,\,\,\, - 0,34;\,\,\,\, - 2,31;\,\,\,\,1,41.\)
B. \( - 2,31;\,\,\,\, - \,0,34;\,\,\,\,\,1,2;\,\,\,\,\,1,41.\)
C. \(1,41;\,\,\,\,1,2;\,\,\,\,\, - 0,34;\,\,\,\,\, - 2,31.\)
D. \( - 0,34;\,\,\,\,1,2;\,\,\,\,1,41;\,\,\,\,\, - 2,31.\,\,\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính hợp lý nếu có thể):
a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\)
b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\)
c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
Bài 2:(1,5 điểm)Tìm x, biết:
a) \(x - \dfrac{{ - 1}}{5} = 1\dfrac{1}{2}\)
b) \( - \dfrac{1}{2} + \left( {x - \dfrac{5}{{11}}} \right) = \dfrac{{ - 3}}{4}\)
c) \(\dfrac{3}{4} + \left( {\dfrac{2}{5} - x} \right) = \dfrac{1}{4}\)
Bài 3:(1,5 điểm)Khối 6 của một trường có 4 lớp. Số học sinh lớp 6A1 bằng \(\dfrac{2}{7}\) tổng số học sinh của ba lớp còn lại. Số học sinh lớp 6A2 bằng \(\dfrac{{11}}{{45}}\) tổng số học sinh khối 6. Số học sinh lớp 6A3 bằng \(\dfrac{7}{{27}}\) tổng số học sinh khối 6. Số học sinh lớp 6A4 là 37 bạn. Hỏi số học sinh lớp 6A1, 6A2, 6A3 là bao nhiêu?
Bài 4: (2,5 điểm) Trên tia An lấy 2 điểm K và Q sao cho AK = 3cm, AQ = 4cm.
a) Tính độ dài đoạn thẳng KQ.
b) Lấy điểm C trên tia Am là tia đối của tia An sao cho AC = 3cm, tính CK.
Điểm A có là trung điểm của đoạn thẳng CK không? Vì sao?
c) Lấy điểm B là trung điểm của đoạn thẳng CA. So sánh BK và AQ?
Bài 5:(0,5 điểm)Tính giá trị của biểu thức: \(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\)
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Giá trị của x trong biểu thức \(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\) là:
A. -8
B. -2
C. 8
D. 2
Câu 2:Hình bên có mấy tia:
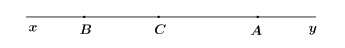
A. 6
B. 3
C. 4
D. 8
Câu 3: Chữ E có bao nhiêu trục đối xứng?
A. \(0\)
B. \(1\)
C. \(2\)
D. \(3\)
Câu 4:Sắp xếp các số \(1,2;\,\,\,\, - 0,34;\,\,\,\, - 2,31;\,\,\,\,1,41\) theo thứ tự giảm dần:
A. \(1,2;\,\,\,\, - 0,34;\,\,\,\, - 2,31;\,\,\,\,1,41.\)
B. \( - 2,31;\,\,\,\, - \,0,34;\,\,\,\,\,1,2;\,\,\,\,\,1,41.\)
C. \(1,41;\,\,\,\,1,2;\,\,\,\,\, - 0,34;\,\,\,\,\, - 2,31.\)
D. \( - 0,34;\,\,\,\,1,2;\,\,\,\,1,41;\,\,\,\,\, - 2,31.\,\,\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính hợp lý nếu có thể):
a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\)
b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\)
c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
Bài 2:(1,5 điểm)Tìm x, biết:
a) \(x - \dfrac{{ - 1}}{5} = 1\dfrac{1}{2}\)
b) \( - \dfrac{1}{2} + \left( {x - \dfrac{5}{{11}}} \right) = \dfrac{{ - 3}}{4}\)
c) \(\dfrac{3}{4} + \left( {\dfrac{2}{5} - x} \right) = \dfrac{1}{4}\)
Bài 3:(1,5 điểm)Khối 6 của một trường có 4 lớp. Số học sinh lớp 6A1 bằng \(\dfrac{2}{7}\) tổng số học sinh của ba lớp còn lại. Số học sinh lớp 6A2 bằng \(\dfrac{{11}}{{45}}\) tổng số học sinh khối 6. Số học sinh lớp 6A3 bằng \(\dfrac{7}{{27}}\) tổng số học sinh khối 6. Số học sinh lớp 6A4 là 37 bạn. Hỏi số học sinh lớp 6A1, 6A2, 6A3 là bao nhiêu?
Bài 4: (2,5 điểm) Trên tia An lấy 2 điểm K và Q sao cho AK = 3cm, AQ = 4cm.
a) Tính độ dài đoạn thẳng KQ.
b) Lấy điểm C trên tia Am là tia đối của tia An sao cho AC = 3cm, tính CK.
Điểm A có là trung điểm của đoạn thẳng CK không? Vì sao?
c) Lấy điểm B là trung điểm của đoạn thẳng CA. So sánh BK và AQ?
Bài 5:(0,5 điểm)Tính giá trị của biểu thức: \(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\)
Phần I: Trắc nghiệm
1. B | 2. A | 3. B | 4. C |
Câu 1
Phương pháp:
Đưa về hai phân số cùng mẫu và so sánh hai phân số bằng nhau hoặc nhân chéo.
Cách giải:
Cách 1:
\(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\)
\(\begin{array}{l}\dfrac{{3x}}{{12}} = \dfrac{{ - 6}}{{12}}\\3x = - 6\\x = - 2\end{array}\)
Cách 2:
\(\begin{array}{l}\dfrac{x}{4} = \dfrac{6}{{ - 12}}\\x = \dfrac{{4.6}}{{ - 12}}\\x = - 2\end{array}\)
Chọn B.
Câu 2
Phương pháp:
Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O.
Cách giải:
Hình trên có 6 tia: Ax, Ay, Bx, By, Cx, Cy.
Chọn A.
Câu 3
Phương pháp:
Sử dụng lý thuyết trục đối xứng của một hình.
Cách giải:
Chữ E có 1 trục đối xứng.
Chọn B.
Câu 4
Phương pháp:
- Số thập phân dương luôn lớn hơn số thập phân âm
- Trong hai số thập phân âm, số nào có số đối lớn hơn thì số đó nhỏ hơn
Cách giải:
Vì \(2,32 > 0,34\) nên \( - 2,32 < - 0,34\)
Do đó, \( - 2,31 < - \,0,34 < 1,2 < 1,41\) nên thứ tự giảm dần của các số là: \(1,41;\,\,\,\,1,2;\,\,\,\,\, - 0,34;\,\,\,\,\, - 2,31.\)
Chọn C.
Phần II: Tự luận
Bài 1
Phương pháp
a) Cộng hai phân số cùng mẫu.
b) Nhóm thích hợp các phân số cùng mẫu.
c) Sử dụng tính chất phân phối của phép nhân và phép cộng.
Cách giải:
a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\)
\(\begin{array}{l} = \dfrac{{ - 7 + 3}}{{16}}\\ = \dfrac{{ - 4}}{{16}}\\ = \dfrac{{ - 1}}{4}\end{array}\)
b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\)
\(\begin{array}{l} = \left( {\dfrac{1}{7} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}} \right) + \dfrac{{ - 1}}{3}\\ = \dfrac{{1 + 10 - 4}}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{7}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{3}{3} + \dfrac{{ - 1}}{3}\\ = \dfrac{{3 - 1}}{3}\\ = \dfrac{2}{3}\end{array}\)
c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
\(\begin{array}{l} = \dfrac{4}{9}.\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{ - 45}}{{26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}.\dfrac{{ - 7 - 45}}{{26}} + \dfrac{1}{3}\\ = \dfrac{4}{9}.\left( { - 2} \right) + \dfrac{1}{3}\\ = \dfrac{{ - 8}}{9} + \dfrac{3}{9}\\ = \dfrac{{ - 8 + 3}}{9}\\ = \dfrac{{ - 5}}{9}\end{array}\)
Bài 2
Phương pháp
Chuyển vế để tìm được \(x\).
Sử dụng phép tính giá trị lũy thừa của một số.
Cách giải:
a) \(x - \frac{{ - 1}}{5} = 1\)
\(\begin{array}{l}\frac{1}{2}x - \frac{{ - 1}}{5} = \frac{3}{2}\\x = \frac{3}{2} + \frac{{ - 1}}{5}\\x = \frac{{13}}{{10}}\end{array}\)
Vậy \(x = \frac{{13}}{{10}}\)
b) \( - \frac{1}{2} + \left( {x - \frac{5}{{11}}} \right) = \frac{{ - 3}}{4}\)
\(\begin{array}{l}x - \frac{5}{{11}} = \frac{{ - 3}}{4} + \frac{1}{2}\\x - \frac{5}{{11}} = \frac{{ - 1}}{4}\\x = \frac{{ - 1}}{4} + \frac{5}{{11}}\\x = \frac{9}{{44}}\end{array}\)
Vậy \(x = \frac{9}{{44}}\)
c) \(\frac{3}{4} + \left( {\frac{2}{5} - x} \right) = \frac{1}{4}\)
\(\frac{2}{5} - x = \frac{1}{4} - \frac{3}{4}\)
\(\frac{2}{5} - x = {\rm{\;}} - \frac{1}{2}\)
\(x = \frac{2}{5} + \frac{1}{2}\)
\(x = \frac{9}{{10}}\)
Vậy \(x = \frac{9}{{10}}\)
Bài 3
Phương pháp
So sánh số học sinh lớp 6A1 với tổng số học sinh khối 6.
So sánh số học sinh lớp 6A4 với tổng số học sinh khối 6.
Tính số học sinh khối 6, từ đó tính số học sinh mỗi lớp 6A1, 6A2, 6A3.
Cách giải:
Vì số học sinh lớp 6A1 bằng \(\dfrac{2}{7}\) tổng số học sinh 3 lớp còn lại => Số học sinh lớp 6A1 bằng \(\dfrac{2}{9}\) tổng số học sinh khối 6.
Số học sinh lớp 6A4 bằng \(1 - \dfrac{2}{9} - \dfrac{{11}}{{45}} - \dfrac{7}{{27}} = \dfrac{{37}}{{135}}\) (tổng số học sinh khối 6)
Số học sinh khối 6 là: \(37:\dfrac{{37}}{{135}} = 135\) (học sinh).
Số học sinh lớp 6A1 là: \(135.\dfrac{2}{9} = 30\) (học sinh).
Số học sinh lớp 6A2 là: \(135.\dfrac{{11}}{{45}} = 33\) (học sinh).
Số học sinh lớp 6A3 là: \(135.\dfrac{7}{{27}} = 35\) (học sinh).
Vậy lớp 6A1 có 30 học sinh, lớp 6A2 có 33 học sinh, lớp 6A3 có 35 học sinh.
Bài 4
Phương pháp
a) Chứng minh K nằm giữa A và Q và suy ra AK + KQ = AQ.
b) Chứng minh A nằm giữa C và K. Tính CK = AC + AK.
Chỉ ra A nằm giữa C, K và AC = AK. Từ đó suy ra A là trung điểm của CK.
c) Tính BA.
Chứng minh A nằm giữa B và K. Tính BK = BA + AK.
So sánh BK và AQ.
Cách giải:
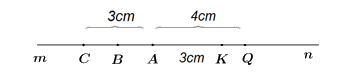
a) Vì AK < AQ (3cm < 4cm) nên K nằm giữa A và Q.
=> AK + KQ = AQ
=> 3 + KQ = 4
=> KQ = 4 – 3
=> KQ = 1 (cm)
b) Vì C và K nằm trên hai tia đối An và Am nên A nằm giữa C và K.
=> CK = AC + AK
=> CK = 3 + 3
=> CK = 6 (cm)
Ta có: A nằm giữa C và K.
AC = AK = 3cm.
=> A là trung điểm của CK.
c) Vì B là trung điểm của AC nên BA = AC : 2 = 3 : 2 = 1,5 (cm).
Vì B, K nằm trên hai tia đối nhau An và Am nên A nằm giữa B và K.
=> BK = BA + AK
=> BK = 1,5 + 3
=> BK = 4,5 (cm)
Mà AQ = 4 (cm)
=> BK > AQ.
Bài 5
Phương pháp
Nhận xét:
\(\dfrac{1}{{1.2}} = 1 - \dfrac{1}{2};\) \(\dfrac{1}{{2.3}} = \dfrac{1}{2} - \dfrac{1}{3};\)\(\dfrac{1}{{3.4}} = \dfrac{1}{3} - \dfrac{1}{4};\)…; \(\dfrac{1}{{2011.2012}} = \dfrac{1}{{2011}} - \dfrac{1}{{2012}}\) sau đó rút gọn các cặp phân số đối nhau rồi thực hiện tính.
Cách giải:
\(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\)
\( = 7.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \ldots + \dfrac{1}{{2011.2012}}} \right)\)
\( = 7.\left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + \ldots + \dfrac{1}{{2011}} - \dfrac{1}{{2012}}} \right)\)
\( = 7.\left( {1 - \dfrac{1}{{2012}}} \right) = \dfrac{{14077}}{{2012}}\)
Đề thi giữa kì 2 Toán 6 - Đề số 1 chương trình Chân trời sáng tạo là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kì. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính đã được học, như số tự nhiên, phân số, số thập phân, hình học cơ bản và các phép toán liên quan.
Thông thường, đề thi giữa kì 2 Toán 6 - Đề số 1 (Chân trời sáng tạo) sẽ có cấu trúc bao gồm:
Các dạng bài tập thường gặp trong đề thi:
Khi giải các bài tập về số tự nhiên, học sinh cần nắm vững các khái niệm cơ bản như:
Ví dụ: Tính 1234 + 5678 = ?
Lời giải: 1234 + 5678 = 6912
Để giải các bài tập về phân số, học sinh cần hiểu rõ:
Ví dụ: Tính 1/2 + 1/3 = ?
Lời giải: 1/2 + 1/3 = 3/6 + 2/6 = 5/6
Khi làm bài tập về số thập phân, cần lưu ý:
Ví dụ: Tính 2.5 x 3.2 = ?
Lời giải: 2.5 x 3.2 = 8
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài tập và đề thi Toán 6, bao gồm cả Đề thi giữa kì 2 Toán 6 - Đề số 1 - Chân trời sáng tạo. Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho học sinh những bài giảng chất lượng và phương pháp học tập hiệu quả.
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kiến thức Toán 6 của bạn!