Chào mừng các em học sinh lớp 6 đến với đề thi học kì 2 môn Toán, đề số 1, chương trình Chân trời sáng tạo. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học và hiểu rõ các dạng bài tập thường gặp trong các kỳ thi.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1. B | 2. A | 3. D | 4. B |
Câu 1
Phương pháp:
Sử dụng công thức: quãng đường = vận tốc . thời gian.
Cách giải:
Độ dài quãng đường AB là: \(26\dfrac{1}{4}.2,4\, = \dfrac{{105}}{4}.\dfrac{{24}}{{10}} = 63\) (km)
Thời gian người ấy đi xe máy đi từ B về A là: \(63:30 = \dfrac{{21}}{{10}} = 2\dfrac{1}{{10}}\) (giờ) \( = 2\) giờ \(6\) phút.
Chọn B.
Câu 2
Phương pháp:
Định nghĩa về góc bẹt.
Cách giải:
Góc bẹt có số đo bằng \({180^0}\).
Chọn A.
Câu 3
Phương pháp:
Sử dụng lý thuyết bảng dữ liệu ban đầu.
Cách giải:
Bảng dữ liệu trên điều tra về loài hoa yêu thích của 30 học sinh lớp 6A1.
Chọn B.
Câu 4
Phương pháp:
Quan sát hình vẽ để xác định một điểm thuộc hay không thuộc một đường thẳng.Cách giải:
Từ hình vẽ ta thấy điểm A, C thuộc đường thẳng a; điểm B, C thuộc đường thẳng b.
Vậy phát biểu sai là hai điểm A, B cùng thuộc đường thẳng a.
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp
a) Nhóm các phân số có cùng mẫu số, rồi thực hiện phép tính cộng hai phân số có cùng mẫu số. Muốn cộng hai phân số có cùng mẫu số ta cộng tử với tử và giữ nguyên mẫu.
b) Thực hiện nhóm như sau: \(\dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5} = \dfrac{1}{5}.\left( {\dfrac{{11}}{{16}} + \dfrac{5}{{16}}} \right) + \dfrac{4}{5}\) rồi sau đó thực hiện phép tính theo thứ tự ưu tiên. Thực hiện phép tính trong ngoặc trước, ngoài ngoặc sau. Nhân chia trước cộng trừ sau.
c) Viết số phần trăm, hỗn số, số thập phân dưới dạng phân số, rồi thực hiện phép tính theo thứ tự nhân chia trước, cộng trừ sau.
d) Thực hiện phép tính lũy thừa, chuyển số phần trăm , hỗ số về phân số. Thực hiện phép tính theo thứ tự ưu tiên: nhân chia trước, cộng trừ sau. Trong ngoặc trước, ngoài ngoặc sau.
Cách giải:
a) \({\kern 1pt} \dfrac{1}{5} + \dfrac{{ - 5}}{{19}} + \dfrac{4}{5} + \dfrac{{ - 4}}{{19}}\) \(\begin{array}{l} = \left( {\dfrac{1}{5} + \dfrac{4}{5}} \right) + \left( {\dfrac{{ - 5}}{{19}} + \dfrac{{ - 4}}{{19}}} \right)\\ = 1 + \dfrac{{ - 9}}{{19}} = \dfrac{{10}}{{19}}\end{array}\) | b) \(\dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5}\) \(\begin{array}{l}{\kern 1pt} = \dfrac{1}{5}.\left( {\dfrac{{11}}{{16}} + \dfrac{5}{{16}}} \right) + \dfrac{4}{5}\\ = \dfrac{1}{5}.1 + \dfrac{4}{5} = 1\end{array}\) |
c) \(25\% {\rm{\;}} - 1\dfrac{1}{2} + 0,5.\dfrac{3}{8}\) \(\begin{array}{l} = \dfrac{{25}}{{100}} - \dfrac{3}{2} + \dfrac{1}{2}.\dfrac{3}{8}\\ = \dfrac{1}{4} - \dfrac{3}{2} + \dfrac{3}{{16}}\\ = \dfrac{{1.4 - 3.8 + 3}}{{16}}\\ = \dfrac{{ - 17}}{{16}}\end{array}\) | d) \({\left( {\frac{{ - 1}}{6}} \right)^2}:\frac{5}{{ - 24}} + \left( {\frac{7}{{25}} - 36\% } \right).\left| { - 8\frac{1}{3}} \right|\) \(=\frac{1}{{36}}:\frac{5}{{ - 24}} + \left( {\frac{7}{{25}} - \frac{{36}}{{100}}} \right).\frac{{25}}{3}\) \(=\frac{1}{{36}}.\frac{{ - 24}}{5} + \left( {\frac{7}{{25}} - \frac{9}{{25}}} \right).\frac{{25}}{3}\) \(=\frac{{ - 2}}{{15}} + {\frac{{ - 2}}{{25}}.\frac{{25}}{3}} \) \(=\frac{{ - 2}}{{15}} + \frac{{ - 2}}{3}\) \(=\frac{{ - 2}}{{15}} + \frac{{ - 10}}{{15}}\) \(=\frac{{ - 12}}{{15}}\)\(=\frac{{ - 4}}{5}\) |
Bài 2
Phương pháp
a) Muốn tìm số bị chia ta lấy thương nhân với số chia.
b) Chuyển \( - \dfrac{1}{2}\) sang vế phải ta đổi dấu thành \( + \dfrac{1}{2}\) ,ta được biểu thức mới có dạng \(\dfrac{2}{3}x = 2\) , từ đó tìm được \(x\).
c) Viết \(40\% \) dưới dạng số thập phân, sử dụng tính chất phân phối của phép nhân đối với phép cộng ta tìm được \(x\).
Cách giải:
a) \(x:\dfrac{2}{5} = \dfrac{{ - 15}}{4}\) \(\begin{array}{l}x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} \dfrac{{ - 15}}{4}.\dfrac{2}{5}\\x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} \dfrac{{ - 3}}{2}\end{array}\) Vậy \(x = \dfrac{{ - 3}}{2}\) | b) \(\dfrac{2}{3}.x - \dfrac{1}{2} = 1\dfrac{1}{2}\) \(\begin{array}{l}\dfrac{2}{3}.x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 1\dfrac{1}{2} + \dfrac{1}{2}\\\dfrac{2}{3}.x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} 1 + \dfrac{1}{2} + \dfrac{1}{2}\\\dfrac{2}{3}.x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} 2\\\,\,\,\,\,x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 2:\dfrac{2}{3}\\\,\,\,\,\,x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} 3\end{array}\) Vậy \(x = 3\) | c) \(0,6.x + 40\% .x = 9\) \(\begin{array}{l}{\kern 1pt} 0,6.x{\kern 1pt} + {\kern 1pt} 0,4.x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 9\\\left( {0,6 + 0,4} \right).x{\kern 1pt} {\kern 1pt} {\kern 1pt} = 9\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x{\kern 1pt} {\kern 1pt} {\kern 1pt} = 9\end{array}\) Vậy \(x{\kern 1pt} {\kern 1pt} {\kern 1pt} = 9\) |
Bài 3
Phương pháp:Muốn tìm \(\dfrac{m}{n}\) của một số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\,\left( {m,n \in N,\,n \ne 0} \right)\)
Cách giải:
a) Số bài kiểm tra đạt loại giỏi là: \(\dfrac{1}{3}.45 = \dfrac{{45}}{3} = 15\) (bài)
Số bài còn lại là: \(45 - 15 = 30\) (bài)
Số bài đạt điểm khá là : \(90\% .30 = \dfrac{{90}}{{100}}.30 = 27\) (bài)
Số bài đạt điểm trung bình là : \(30 - 27 = 3\) (bài)
b) Tỷ số phần trăm số bài đạt điểm trung bình so với tổng số bài kiểm tra là : \(\dfrac{3}{{45}} \times 100 \simeq 6.7\% \)
Đáp số : a)\(3\) bài. b) \(6,7\% \)
Bài 4
Phương pháp
Vẽ tia, tia đối, vẽ điểm, trung điểm đoạn thẳng.
Chứng minh một điểm nằm giữa hai điểm còn lại, tính độ dài đoạn thẳng, chứng minh trung điểm.
Cách giải:
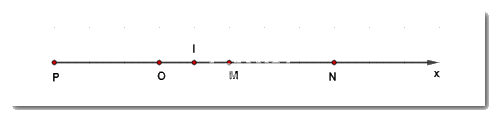
a) Hai điểm M,N cùng thuộc tia \(Ox\) và \(OM < ON(2cm < 5cm)\) nên điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
Khi đó \(OM + MN = ON\) hay \(MN = ON - OM = 5 - 2 = 3cm\).
b) \(MN = OP = 3cm\).
c) \(I\) là trung điểm của \(OM\) nên \(IO = IM = \dfrac{{OM}}{2} = 1cm\).
\(I\) là trung điểm của \(OM\) nên \(I\) thuộc tia \(Ox\).
\(P\) thuộc tia đối của tia \(Ox\) nên \(O\) nằm giữa \(I\) và \(P\).
Khi đó ta có \(OP + OI = IP\) hay \(IP = OP + OI = 3 + 1 = 4cm\).
d) \(O\) và \(N\) nằm khác phía so với điềm \(I\); \(O\) và \({\rm{P}}\) nằm cùng phía so với điểm \(I\) nên \(N\) và \(P\) nằm khác phía so với điểm \(I\).
Ta tính được \(IN = 4cm\).
Do vậy \(IP = IN = 4cm\).
Vậy \(I\) là trung điểm của đoạn thẳng \(NP.\)
Bài 5
Phương pháp: Ta chứng minh \(S > 2\) và \(S < 5\).
Ta thấy :
\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right)\\ > 5.\left( {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{100.101}}} \right)\end{array}\)
Rồi sử dụng : \(\dfrac{1}{{n.\left( {n + 1} \right)}} = \dfrac{1}{n} - \dfrac{1}{{n + 1}}\) để thu gọn S rồi so sánh S với 2.
Tương tự khi so sánh S với 5.
Cách giải:
Ta có:
\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right) > 5.\left( {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{100.101}}} \right) > 5.\left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{100}} - \dfrac{1}{{101}}} \right)\\ > 5.\left( {\dfrac{1}{2} - \dfrac{1}{{101}}} \right) > \dfrac{5}{2} > 2\\ \Rightarrow S > 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\end{array}\)
\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right) < 5.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{99.100}}} \right)\\ < 5.\left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{99}} - \dfrac{1}{{100}}} \right) < 5.\left( {1 - \dfrac{1}{{100}}} \right) < 5\\ \Rightarrow S < 5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) : \(2 < S < 5\) (đpcm).
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Một người đi xe máy đoạn đường AB với vận tốc \(26\dfrac{1}{4}\) km/h hết \(2,4\) giờ. Lúc về, người ấy đi với vận tốc \(30\) km/h. Tính thời gian người ấy đi từ B đến A?
A. \(2\) giờ \(5\) phút B. \(2\) giờ \(6\) phút C. \(2\) giờ D. \(2\) giờ \(4\) phút
Câu 2:Góc bẹt có số đo bằng:
A. \({180^0}\) B. \({90^0}\) C. \({60^0}\) D. \({0^0}\)
Câu 3: Gieo một con xúc xắc \(4\) mặt \(50\) lần và quan sát số ghi trên đỉnh của con xúc xắc, ta được kết quả như sau:

Tính xác suất thực nghiệm để gieo được đỉnh có số chẵn:
A. \(\dfrac{9}{{50}}\) B. \(\dfrac{{14}}{{50}}\) C. \(\dfrac{{15}}{{50}}\) D. \(\dfrac{{23}}{{50}}\)
Câu 4:
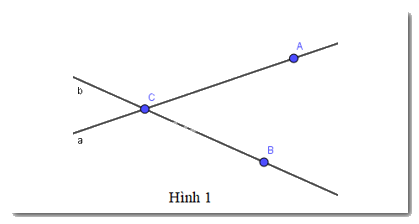
Chọn phát biểu sai trong các phát biểu sau:
A. Điểm A thuộc đường thẳng a
B. Hai điểm A, B cùng thuộc đường thẳng a
C. Điểm C thuộc đường thẳng b
D. Hai điểm B, C cùng thuộc đường thẳng b
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể):
a) \({\kern 1pt} \dfrac{1}{5} + \dfrac{{ - 5}}{{19}} + \dfrac{4}{5} + \dfrac{{ - 4}}{{19}}\) b) \({\kern 1pt} \dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5}\)
c) \({\kern 1pt} 25\% {\rm{\;}} - 1\dfrac{1}{2} + 0,5.\dfrac{3}{8}\) d) \({\kern 1pt} {\left( {\dfrac{{ - 1}}{6}} \right)^2}:\dfrac{5}{{ - 24}} + \left( {\dfrac{7}{{25}} - 36\% } \right).\left| { - 8\dfrac{1}{3}} \right|\)
Bài 2:(1,5 điểm)Tìm x, biết:
Tìm \(x\), biết:
a) \({\kern 1pt} x:\dfrac{2}{5} = \dfrac{{ - 15}}{4}\)b) \({\kern 1pt} \dfrac{2}{3}.x - \dfrac{1}{2} = 1\dfrac{1}{2}\)c) \({\kern 1pt} 0,6.x + 40\% x = 9\)
Bài 3:(1,5 điểm)Có một tập bài kiểm tra gồm 45 bài được xếp thành ba loại: Giỏi, khá và trung bình. Trong đó số bài đạt điểm giỏi bằng \(\dfrac{1}{3}\) tổng số bài kiểm tra. Số bài đạt điểm khá bằng \(90\% \) số bài còn lại.
a) Tính số bài trung bình.
b) Tính tỷ số phần trăm số bài đạt điểm trung bình so với tổng số bài kiểm tra.
Bài 4: (2,5 điểm) Cho hai điểm \(M,N\) thuộc tia \(Ox\) sao cho \(OM = 2cm;ON = 5cm\). Điểm \(P\) thuộc tia đối của tia \(Ox\) sao cho \(OP = 3cm\).
a) Điểm \(M\) có nằm giữa hai điểm \(O\) và \(N\) không? Tại sao? Tính \(MN.\)
b) So sánh\(MN\) và \(OP.\)
c) Gọi \(I\) là trung điểm của \(OM\). Tính \(IO\) và \(IP.\)
d) Điểm \(I\) có là trung điểm của \(NP\) không? Tại sao?
Bài 5:(0,5 điểm)Cho \(S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}\)
Chứng minh rằng \(2 < S < 5\)
Tải về
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Một người đi xe máy đoạn đường AB với vận tốc \(26\dfrac{1}{4}\) km/h hết \(2,4\) giờ. Lúc về, người ấy đi với vận tốc \(30\) km/h. Tính thời gian người ấy đi từ B đến A?
A. \(2\) giờ \(5\) phút B. \(2\) giờ \(6\) phút C. \(2\) giờ D. \(2\) giờ \(4\) phút
Câu 2:Góc bẹt có số đo bằng:
A. \({180^0}\) B. \({90^0}\) C. \({60^0}\) D. \({0^0}\)
Câu 3: Gieo một con xúc xắc \(4\) mặt \(50\) lần và quan sát số ghi trên đỉnh của con xúc xắc, ta được kết quả như sau:

Tính xác suất thực nghiệm để gieo được đỉnh có số chẵn:
A. \(\dfrac{9}{{50}}\) B. \(\dfrac{{14}}{{50}}\) C. \(\dfrac{{15}}{{50}}\) D. \(\dfrac{{23}}{{50}}\)
Câu 4:
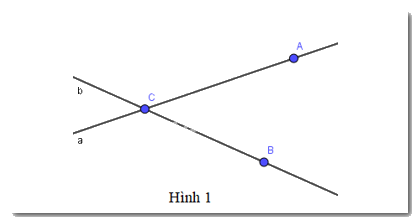
Chọn phát biểu sai trong các phát biểu sau:
A. Điểm A thuộc đường thẳng a
B. Hai điểm A, B cùng thuộc đường thẳng a
C. Điểm C thuộc đường thẳng b
D. Hai điểm B, C cùng thuộc đường thẳng b
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể):
a) \({\kern 1pt} \dfrac{1}{5} + \dfrac{{ - 5}}{{19}} + \dfrac{4}{5} + \dfrac{{ - 4}}{{19}}\) b) \({\kern 1pt} \dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5}\)
c) \({\kern 1pt} 25\% {\rm{\;}} - 1\dfrac{1}{2} + 0,5.\dfrac{3}{8}\) d) \({\kern 1pt} {\left( {\dfrac{{ - 1}}{6}} \right)^2}:\dfrac{5}{{ - 24}} + \left( {\dfrac{7}{{25}} - 36\% } \right).\left| { - 8\dfrac{1}{3}} \right|\)
Bài 2:(1,5 điểm)Tìm x, biết:
Tìm \(x\), biết:
a) \({\kern 1pt} x:\dfrac{2}{5} = \dfrac{{ - 15}}{4}\)b) \({\kern 1pt} \dfrac{2}{3}.x - \dfrac{1}{2} = 1\dfrac{1}{2}\)c) \({\kern 1pt} 0,6.x + 40\% x = 9\)
Bài 3:(1,5 điểm)Có một tập bài kiểm tra gồm 45 bài được xếp thành ba loại: Giỏi, khá và trung bình. Trong đó số bài đạt điểm giỏi bằng \(\dfrac{1}{3}\) tổng số bài kiểm tra. Số bài đạt điểm khá bằng \(90\% \) số bài còn lại.
a) Tính số bài trung bình.
b) Tính tỷ số phần trăm số bài đạt điểm trung bình so với tổng số bài kiểm tra.
Bài 4: (2,5 điểm) Cho hai điểm \(M,N\) thuộc tia \(Ox\) sao cho \(OM = 2cm;ON = 5cm\). Điểm \(P\) thuộc tia đối của tia \(Ox\) sao cho \(OP = 3cm\).
a) Điểm \(M\) có nằm giữa hai điểm \(O\) và \(N\) không? Tại sao? Tính \(MN.\)
b) So sánh\(MN\) và \(OP.\)
c) Gọi \(I\) là trung điểm của \(OM\). Tính \(IO\) và \(IP.\)
d) Điểm \(I\) có là trung điểm của \(NP\) không? Tại sao?
Bài 5:(0,5 điểm)Cho \(S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}\)
Chứng minh rằng \(2 < S < 5\)
Phần I: Trắc nghiệm
1. B | 2. A | 3. D | 4. B |
Câu 1
Phương pháp:
Sử dụng công thức: quãng đường = vận tốc . thời gian.
Cách giải:
Độ dài quãng đường AB là: \(26\dfrac{1}{4}.2,4\, = \dfrac{{105}}{4}.\dfrac{{24}}{{10}} = 63\) (km)
Thời gian người ấy đi xe máy đi từ B về A là: \(63:30 = \dfrac{{21}}{{10}} = 2\dfrac{1}{{10}}\) (giờ) \( = 2\) giờ \(6\) phút.
Chọn B.
Câu 2
Phương pháp:
Định nghĩa về góc bẹt.
Cách giải:
Góc bẹt có số đo bằng \({180^0}\).
Chọn A.
Câu 3
Phương pháp:
Sử dụng lý thuyết bảng dữ liệu ban đầu.
Cách giải:
Bảng dữ liệu trên điều tra về loài hoa yêu thích của 30 học sinh lớp 6A1.
Chọn B.
Câu 4
Phương pháp:
Quan sát hình vẽ để xác định một điểm thuộc hay không thuộc một đường thẳng.Cách giải:
Từ hình vẽ ta thấy điểm A, C thuộc đường thẳng a; điểm B, C thuộc đường thẳng b.
Vậy phát biểu sai là hai điểm A, B cùng thuộc đường thẳng a.
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp
a) Nhóm các phân số có cùng mẫu số, rồi thực hiện phép tính cộng hai phân số có cùng mẫu số. Muốn cộng hai phân số có cùng mẫu số ta cộng tử với tử và giữ nguyên mẫu.
b) Thực hiện nhóm như sau: \(\dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5} = \dfrac{1}{5}.\left( {\dfrac{{11}}{{16}} + \dfrac{5}{{16}}} \right) + \dfrac{4}{5}\) rồi sau đó thực hiện phép tính theo thứ tự ưu tiên. Thực hiện phép tính trong ngoặc trước, ngoài ngoặc sau. Nhân chia trước cộng trừ sau.
c) Viết số phần trăm, hỗn số, số thập phân dưới dạng phân số, rồi thực hiện phép tính theo thứ tự nhân chia trước, cộng trừ sau.
d) Thực hiện phép tính lũy thừa, chuyển số phần trăm , hỗ số về phân số. Thực hiện phép tính theo thứ tự ưu tiên: nhân chia trước, cộng trừ sau. Trong ngoặc trước, ngoài ngoặc sau.
Cách giải:
a) \({\kern 1pt} \dfrac{1}{5} + \dfrac{{ - 5}}{{19}} + \dfrac{4}{5} + \dfrac{{ - 4}}{{19}}\) \(\begin{array}{l} = \left( {\dfrac{1}{5} + \dfrac{4}{5}} \right) + \left( {\dfrac{{ - 5}}{{19}} + \dfrac{{ - 4}}{{19}}} \right)\\ = 1 + \dfrac{{ - 9}}{{19}} = \dfrac{{10}}{{19}}\end{array}\) | b) \(\dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5}\) \(\begin{array}{l}{\kern 1pt} = \dfrac{1}{5}.\left( {\dfrac{{11}}{{16}} + \dfrac{5}{{16}}} \right) + \dfrac{4}{5}\\ = \dfrac{1}{5}.1 + \dfrac{4}{5} = 1\end{array}\) |
c) \(25\% {\rm{\;}} - 1\dfrac{1}{2} + 0,5.\dfrac{3}{8}\) \(\begin{array}{l} = \dfrac{{25}}{{100}} - \dfrac{3}{2} + \dfrac{1}{2}.\dfrac{3}{8}\\ = \dfrac{1}{4} - \dfrac{3}{2} + \dfrac{3}{{16}}\\ = \dfrac{{1.4 - 3.8 + 3}}{{16}}\\ = \dfrac{{ - 17}}{{16}}\end{array}\) | d) \({\left( {\frac{{ - 1}}{6}} \right)^2}:\frac{5}{{ - 24}} + \left( {\frac{7}{{25}} - 36\% } \right).\left| { - 8\frac{1}{3}} \right|\) \(=\frac{1}{{36}}:\frac{5}{{ - 24}} + \left( {\frac{7}{{25}} - \frac{{36}}{{100}}} \right).\frac{{25}}{3}\) \(=\frac{1}{{36}}.\frac{{ - 24}}{5} + \left( {\frac{7}{{25}} - \frac{9}{{25}}} \right).\frac{{25}}{3}\) \(=\frac{{ - 2}}{{15}} + {\frac{{ - 2}}{{25}}.\frac{{25}}{3}} \) \(=\frac{{ - 2}}{{15}} + \frac{{ - 2}}{3}\) \(=\frac{{ - 2}}{{15}} + \frac{{ - 10}}{{15}}\) \(=\frac{{ - 12}}{{15}}\)\(=\frac{{ - 4}}{5}\) |
Bài 2
Phương pháp
a) Muốn tìm số bị chia ta lấy thương nhân với số chia.
b) Chuyển \( - \dfrac{1}{2}\) sang vế phải ta đổi dấu thành \( + \dfrac{1}{2}\) ,ta được biểu thức mới có dạng \(\dfrac{2}{3}x = 2\) , từ đó tìm được \(x\).
c) Viết \(40\% \) dưới dạng số thập phân, sử dụng tính chất phân phối của phép nhân đối với phép cộng ta tìm được \(x\).
Cách giải:
a) \(x:\dfrac{2}{5} = \dfrac{{ - 15}}{4}\) \(\begin{array}{l}x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} \dfrac{{ - 15}}{4}.\dfrac{2}{5}\\x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} \dfrac{{ - 3}}{2}\end{array}\) Vậy \(x = \dfrac{{ - 3}}{2}\) | b) \(\dfrac{2}{3}.x - \dfrac{1}{2} = 1\dfrac{1}{2}\) \(\begin{array}{l}\dfrac{2}{3}.x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 1\dfrac{1}{2} + \dfrac{1}{2}\\\dfrac{2}{3}.x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} 1 + \dfrac{1}{2} + \dfrac{1}{2}\\\dfrac{2}{3}.x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} 2\\\,\,\,\,\,x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 2:\dfrac{2}{3}\\\,\,\,\,\,x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} 3\end{array}\) Vậy \(x = 3\) | c) \(0,6.x + 40\% .x = 9\) \(\begin{array}{l}{\kern 1pt} 0,6.x{\kern 1pt} + {\kern 1pt} 0,4.x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 9\\\left( {0,6 + 0,4} \right).x{\kern 1pt} {\kern 1pt} {\kern 1pt} = 9\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x{\kern 1pt} {\kern 1pt} {\kern 1pt} = 9\end{array}\) Vậy \(x{\kern 1pt} {\kern 1pt} {\kern 1pt} = 9\) |
Bài 3
Phương pháp:Muốn tìm \(\dfrac{m}{n}\) của một số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\,\left( {m,n \in N,\,n \ne 0} \right)\)
Cách giải:
a) Số bài kiểm tra đạt loại giỏi là: \(\dfrac{1}{3}.45 = \dfrac{{45}}{3} = 15\) (bài)
Số bài còn lại là: \(45 - 15 = 30\) (bài)
Số bài đạt điểm khá là : \(90\% .30 = \dfrac{{90}}{{100}}.30 = 27\) (bài)
Số bài đạt điểm trung bình là : \(30 - 27 = 3\) (bài)
b) Tỷ số phần trăm số bài đạt điểm trung bình so với tổng số bài kiểm tra là : \(\dfrac{3}{{45}} \times 100 \simeq 6.7\% \)
Đáp số : a)\(3\) bài. b) \(6,7\% \)
Bài 4
Phương pháp
Vẽ tia, tia đối, vẽ điểm, trung điểm đoạn thẳng.
Chứng minh một điểm nằm giữa hai điểm còn lại, tính độ dài đoạn thẳng, chứng minh trung điểm.
Cách giải:
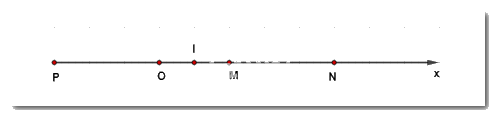
a) Hai điểm M,N cùng thuộc tia \(Ox\) và \(OM < ON(2cm < 5cm)\) nên điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
Khi đó \(OM + MN = ON\) hay \(MN = ON - OM = 5 - 2 = 3cm\).
b) \(MN = OP = 3cm\).
c) \(I\) là trung điểm của \(OM\) nên \(IO = IM = \dfrac{{OM}}{2} = 1cm\).
\(I\) là trung điểm của \(OM\) nên \(I\) thuộc tia \(Ox\).
\(P\) thuộc tia đối của tia \(Ox\) nên \(O\) nằm giữa \(I\) và \(P\).
Khi đó ta có \(OP + OI = IP\) hay \(IP = OP + OI = 3 + 1 = 4cm\).
d) \(O\) và \(N\) nằm khác phía so với điềm \(I\); \(O\) và \({\rm{P}}\) nằm cùng phía so với điểm \(I\) nên \(N\) và \(P\) nằm khác phía so với điểm \(I\).
Ta tính được \(IN = 4cm\).
Do vậy \(IP = IN = 4cm\).
Vậy \(I\) là trung điểm của đoạn thẳng \(NP.\)
Bài 5
Phương pháp: Ta chứng minh \(S > 2\) và \(S < 5\).
Ta thấy :
\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right)\\ > 5.\left( {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{100.101}}} \right)\end{array}\)
Rồi sử dụng : \(\dfrac{1}{{n.\left( {n + 1} \right)}} = \dfrac{1}{n} - \dfrac{1}{{n + 1}}\) để thu gọn S rồi so sánh S với 2.
Tương tự khi so sánh S với 5.
Cách giải:
Ta có:
\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right) > 5.\left( {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{100.101}}} \right) > 5.\left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{100}} - \dfrac{1}{{101}}} \right)\\ > 5.\left( {\dfrac{1}{2} - \dfrac{1}{{101}}} \right) > \dfrac{5}{2} > 2\\ \Rightarrow S > 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\end{array}\)
\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right) < 5.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{99.100}}} \right)\\ < 5.\left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{99}} - \dfrac{1}{{100}}} \right) < 5.\left( {1 - \dfrac{1}{{100}}} \right) < 5\\ \Rightarrow S < 5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) : \(2 < S < 5\) (đpcm).
Đề thi học kì 2 Toán 6 - Đề số 1 chương trình Chân trời sáng tạo là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau một học kì học tập. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính đã được học trong chương trình.
Thông thường, đề thi học kì 2 Toán 6 - Đề số 1 - Chân trời sáng tạo sẽ bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi học kì 2 Toán 6 - Đề số 1 - Chân trời sáng tạo bao gồm:
Ví dụ: Tính (-5) + 3 - (-2). Giải: (-5) + 3 - (-2) = -5 + 3 + 2 = 0
Để giải các bài toán về số nguyên, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số nguyên.
Ví dụ: Tính 2/3 + 1/4. Giải: 2/3 + 1/4 = 8/12 + 3/12 = 11/12
Để giải các bài toán về phân số, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia phân số, quy đồng mẫu số và rút gọn phân số.
Ví dụ: Tính 2,5 x 3,2. Giải: 2,5 x 3,2 = 8
Để giải các bài toán về số thập phân, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số thập phân.
Để đạt kết quả tốt trong kỳ thi học kì 2 Toán 6, học sinh cần:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài tập và đề thi Toán 6, bao gồm cả Đề thi học kì 2 Toán 6 - Đề số 1 - Chân trời sáng tạo. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn sẽ giúp các em học toán hiệu quả và đạt kết quả cao.
Trước khi vào phòng thi, hãy:
Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi học kì 2 Toán 6!