Chào mừng các em học sinh lớp 6 đến với đề thi học kì 2 môn Toán, đề số 10, chương trình Chân trời sáng tạo. Đề thi này được thiết kế để giúp các em ôn luyện và củng cố kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi với cấu trúc tương tự đề thi chính thức, giúp các em làm quen với dạng bài và rèn luyện kỹ năng giải quyết vấn đề. Chúc các em ôn thi tốt!
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1. D | 2. D | 3. D | 4. B |
Câu 1
Phương pháp:
Vẽ các hình đề bài cho và tìm trục đối xứng của mỗi hình.
Cách giải:
Hình chữ nhật, hình thoi, hình sao vàng 5 cánh đều là những hình có trục đối xứng.
Hình thang cân có trục đối xứng, còn hình thang có hai cạnh bên không bằng nhau sẽ không có trục đối xứng.
ChọnD.
Câu 2
Phương pháp:
Phân loại góc.
Cách giải:
- Góc lớn hơn góc vuông là góc tù hoặc góc bẹt.
- Góc nhỏ hơn góc bẹt là góc tù, góc vuông hoặc góc nhọn.
- Góc lớn hơn góc nhọn là góc tù, góc vuông hoặc góc bẹt.
- Góc lớn hơn góc vuông và nhỏ hơn góc bẹt là góc tù
Chọn D.
Câu 3
Phương pháp:
Tìm cột cân nặng 41 kg và đối chiếu số học sinh.
Cách giải:
Dựa vào bảng thống kê ta thấy có 3 học sinh nặng 41 kilogam.
Chọn D.
Câu 4
Phương pháp:
Liệt kê các khả năng có thể xảy ra.
Cách giải:
Tung đồng xu một lần thì có 2 kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là sấp hoặc ngửa.
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp:
a) Áp dụng tính chất giao hoán và kết hợp của phép nhân, khi nhân nhiều số nguyên, ta có thể đổi chỗ hoặc nhóm các phân số lại theo bất cứ cách nào sao cho việc tính toán được thuận tiện.
b) Thực hiện theo thứ tự thực hiện các phép tính: lũy thừa, nhân, chia trước, cộng trừ sau.
c) Thực hiện phép chia trước, sau đó thực hiện phép trừ hai phân số.
d) Sử dụng tính chất phân phối của phép nhân với phép cộng.
\(a.b + a.c = a.\left( {b + c} \right)\)
Cách giải:
\(\begin{array}{l}a)\,25.\left( { - 27} \right).4\\ = \left( {25.4} \right).\left( { - 27} \right)\\ = 100.\left( { - 27} \right)\\ = - 2700\end{array}\) \(\begin{array}{l}b)\, - 51 + 24:\left( { - 4} \right) - 37.{\left( { - 2} \right)^2}\\ = - 51 + \left( { - 6} \right) - 37.4\\ = - 57 - 148\\ = - 205\end{array}\)
\(\begin{array}{l}c)\,\dfrac{{19}}{{12}} - \dfrac{7}{{22}}:\dfrac{{21}}{{11}}\\ = \dfrac{{19}}{{12}} - \dfrac{7}{{22}}.\dfrac{{11}}{{21}}\\ = \dfrac{{19}}{{12}} - \dfrac{1}{6}\\ = \dfrac{{19}}{{12}} - \dfrac{2}{{12}}\\ = \dfrac{{17}}{{12}}\end{array}\) \(\begin{array}{l}d)\,\dfrac{5}{9}.\dfrac{7}{{13}} - \dfrac{5}{9}.\dfrac{3}{{13}} + \dfrac{5}{{13}}.\dfrac{{61}}{9}\\ = \dfrac{5}{9}.\left( {\dfrac{7}{{13}} - \dfrac{3}{{13}} + \dfrac{{61}}{{13}}} \right)\\ = \dfrac{5}{9}.\dfrac{{65}}{{13}}\\ = \dfrac{{25}}{9}\end{array}\)
Câu 2
Phương pháp:
a) Chuyển 12 từ vế phải sang vế trái thành \( - 12\) , rồi thực hiện cộng trừ hai số nguyên khác dấu ở vế trái. Từ đó ta tìm được x dễ dàng bằng cách lấy kết quả chia cho 5.
b) Chuyển \(\dfrac{{ - 1}}{2}\) ở vế phải sang vế trái trở thành \(\dfrac{{ + 1}}{2}\) , rồi thực hiện phép cộng hai phân số khác mẫu số, rồi tìm x bằng cách lấy kết quả thu được ở bước trước chia cho \(\dfrac{2}{3}\)
2) Biến đổi \(\dfrac{{n + 8}}{{n + 7}} = 1 + \dfrac{1}{{n + 7}}\) khi đó, để \(n + 8\) chia hết cho \(n + 7\) thì \(\dfrac{1}{{n + 7}}\) là một số nguyên, hay \(n + 7\) là ước của 1.
Cách giải:
1) \(\begin{array}{l}a)\,5x + 12 = 2\\\,\,\,\,\,\,5x\,\,\,\,\,\,\,\,\,\,\, = 2 - 12\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = - \,10:5\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = - 2\end{array}\) | \(\begin{array}{l}b)\dfrac{2}{3}x - \dfrac{1}{2} = \dfrac{1}{{10}}\\\,\,\,\,\,\dfrac{2}{3}x\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{{10}} + \dfrac{1}{2}\\\,\,\,\,\,\dfrac{2}{3}x\,\,\,\,\,\,\,\,\,\, = \,\,\dfrac{6}{{10}}\\\,\,\,\,\,\dfrac{2}{3}x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{5}\\\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\, = \dfrac{3}{5}:\dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{9}{{10}}\end{array}\) |
2) Ta có: \(\dfrac{{n + 8}}{{n + 7}} = \dfrac{{n + 7 + 1}}{{n + 7}} = \dfrac{{n + 7}}{{n + 7}} + \dfrac{1}{{n + 7}} = 1 + \dfrac{1}{{n + 7}}\,\,\left( {n \ne - 7} \right)\)
Để \(n + 8\) chia hết cho \(n + 7\) thì \(n + 7\) là ước của \(1\) .
Do đó:
+) \(\begin{array}{l}n + 7 = 1\\n\,\,\,\,\,\,\,\,\, = 1 - 7\\n\,\,\,\,\,\,\,\,\, = - 6\end{array}\)
+) \(\begin{array}{l}n + 7 = - 1\\n\,\,\,\,\,\,\,\,\, = - 1 - 7\\n\,\,\,\,\,\,\,\,\, = - 8\end{array}\)
Vậy \(n = - 6;\,\,\,\,n = - 8\) thì \(n + 8\) chia hết cho \(n + 7\)
Câu 3
Phương pháp:
1) a) tính số học sinh trung bình của lớp, biết rằng số học sinh trung bình chiếm \(\dfrac{5}{{12}}\) số học sinh cả lớp.
Chú ý: Muốn tìm \(\dfrac{m}{n}\) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\,\,\,\left( {m,n \in N,\,n \ne 0} \right).\)
Tìm số học sinh khá, rồi số học sinh giỏi .
b) Tìm tỉ số phần trăm số học sinh giỏi so với số học sinh cả lớp, ta lấy số học sinh giỏi chia cho số học sinh cả lớp rồi nhân với 100, viết thêm kí hiệu % vào bên phải kết quả tìm được.
2) Tìm số phần công việc mỗi người làm được trong 1 giờ (ta lấy 1 chia cho số giờ hoàn thành công việc của từng người. Muốn biết cả hai người làm chung trong 1 giờ được bao nhiêu phần công việc, ta cộng tổng số phần công việc của mỗi người trong 1 giờ lại.
Cách giải:
1) Số học sinh trung bình là: \(\dfrac{5}{{12}}.48 = 20\) (học sinh)
Số học sinh còn lại là: \(48 - 20 = 28\) (học sinh)
a) Số học sinh khá là: \(28.\dfrac{4}{7} = 16\) (học sinh)
Số học sinh giỏi là: \(28 - 16 = 12\) (học sinh)
b) Số học sinh giỏi chiếm số phần trăm so với số học sinh cả lớp là : \(\left( {12:48} \right).100\% = 25\% \)
2) Một giờ người thứ nhất làm được là : \(\dfrac{1}{4}\) (công việc)
Một giờ người thứ hai làm được là : \(\dfrac{1}{3}\) (công việc)
Nếu làm chung, trong một giờ cả hai người làm được là : \(\dfrac{1}{4} + \dfrac{1}{3} = \dfrac{7}{{12}}\) (công việc)
Vậy nếu làm chung thì 1 giờ cả hai người làm được \(\dfrac{7}{{12}}\) công việc
Câu 4
Phương pháp:
a) Chỉ ra \(B\) nằm giữa O và A, ta có: OB + BA = OA từ đó tính được AB.
b) Tính độ dài đoạn BC và BD
Chỉ ra B nằm giữa C và D nên BD + BC = CD, từ đó tính được CD
Cách giải:
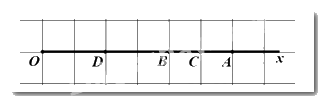
a) Trên tia \(Ox,OB < OA\left( {4cm < 6cm} \right)\) nên B nằm giữa O và A
\(\begin{array}{*{20}{l}}{ \Rightarrow OB + BA = OA}\\{ \Rightarrow 4 + BA = 6}\\{ \Rightarrow AB = 2\left( {cm} \right)}\end{array}\)
b) Vì \(C\) là trung điểm của AB nên \(CA = CB = \dfrac{1}{2}AB = 1\left( {cm} \right)\)
Vì \(D\) là trung điểm của OB nên \(DB = DO = \dfrac{1}{2}OB = 3\left( {cm} \right)\)
Vì \(B\) nằm giữa C và D nên \(BD + BC = CD \Rightarrow CD = 2 + 1 = 3\left( {cm} \right)\)
Câu 5
Phương pháp:
a) Thực hiện phép tính \(\dfrac{2}{{3.5}}\), quy đồng mẫu số hai phân số \(\dfrac{1}{3} - \dfrac{1}{5}\), rồi so sánh hai kết quả với nhau.
b) Nhận thấy:
\(\dfrac{2}{{3.5}} = \dfrac{1}{3} - \dfrac{1}{5};\,\,\,\,\,\,\,\,\dfrac{2}{{5.7}} = \dfrac{1}{5} - \dfrac{1}{7}\,\,\,\,;\,\,\,\,\,\,.....\,\,;\,\,\,\dfrac{2}{{2017.2019}} = \dfrac{1}{{2017}} - \dfrac{1}{{2019}}\)
Thay vào biểu thức của S, ta tính được tổng.
Cách giải:
a) Ta có: \(\dfrac{2}{{3.5}} = \dfrac{2}{{15}}\) và \(\dfrac{1}{3} - \dfrac{1}{5} = \dfrac{{5 - 3}}{{15}} = \dfrac{2}{{15}}\)
Vậy: \(\dfrac{2}{{3.5}} = \dfrac{1}{3} - \dfrac{1}{5}\)
b) Ta có:
\(\begin{array}{l}S = \dfrac{2}{{3.5}} + \dfrac{2}{{5.7}} + \dfrac{2}{{7.9}} + ... + \dfrac{2}{{2017.2019}}\\\,\,\,\, = \dfrac{1}{3} - \dfrac{1}{5} + \dfrac{1}{5} - \dfrac{1}{7} + \dfrac{1}{7} - \dfrac{1}{9} + ... + \dfrac{1}{{2017}} - \dfrac{1}{{2019}}\\\,\,\,\, = \dfrac{1}{3} - \dfrac{1}{{2019}}\\\,\,\,\, = \dfrac{{672}}{{2019}} = \dfrac{{224}}{{673}}\end{array}\)
Vậy \(S = \dfrac{{224}}{{673}}\)
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Hình nào sau đây không có trục đối xứng?
A. Hình chữ nhật B. Hình ngôi sao vàng 5 cánh
C. Hình thoi D. Hình thang có hai cạnh bên không bằng nhau
Câu 2. Câu nào đúng?
A. Góc lớn hơn góc vuông là góc tù.
B. Góc nhỏ hơn góc bẹt là góc tù.
C. Góc lớn hơn góc nhọn là góc tù.
D. Góc lớn hơn góc vuông, nhỏ hơn góc bẹt là góc tù
Câu 3. Bảng thống kê về cân nặng (theo đơn vị kilogam) của 15 học sinh lớp 6 như sau:

Theo bảng thống kê trên thì số học sinh nặng 41 kilogam là:
A. 1 B. 4 C. 2 D. 3
Câu 4. Tung đồng xu một lần. Có bao nhiêu kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu?
A. 1 B. 2 C. 3 D. 4
Phần II. Tự luận
Câu 1 Thực hiện các phép tính
\(a)\,25.\left( { - 27} \right).4\) \(b)\, - 51 + 24:\left( { - 4} \right) - 37.{\left( { - 2} \right)^2}\)
\(c)\,\dfrac{{19}}{{12}} - \dfrac{7}{{22}}:\dfrac{{21}}{{11}}\) \(d)\,\dfrac{5}{9}.\dfrac{7}{{13}} - \dfrac{5}{9}.\dfrac{3}{{13}} + \dfrac{5}{{13}}.\dfrac{{61}}{9}\)
Câu 2
1) Tìm \(x\), biết:
\(a)\,5x + 12 = 2\) \(b)\dfrac{2}{3}x - \dfrac{1}{2} = \dfrac{1}{{10}}\)
2) Tìm các giá trị nguyên của \(n\) để \(n + 8\) chia hết cho \(n + 7\)
Câu 3
1) Một lớp học có 48 học sinh gồm 3 loại : Giỏi, Khá, Trung bình. Học sinh trung bình chiếm \(\dfrac{5}{{12}}\) số học sinh cả lớp. Số học sinh khá bằng \(\dfrac{4}{7}\) số học sinh còn lại.
a) Tìm số học sinh mỗi loại của lớp?
b) Tính tỉ số phần trăm số học sinh giỏi so với số học sinh cả lớp?
2) Hai người cùng làm một công việc.Nếu làm riêng, người thứ nhất phải mất 4 giờ, người thứ hai 3 giờ. Hỏi nếu làm chung thì một giờ cả hai người làm được mấy phần công việc?
Câu 4 Trên tia Ox, vẽ các điểm A,B sao cho \(OA = 6cm,OB = 4cm\).
a) Tính độ dài đoạn thẳng AB.
b) Vẽ điểm \(C\) là trung điểm AB, điểm \(D\) là trung điểm OA. Tính độ dài đoạn thẳng CD.
Câu 5
a) So sánh: \(\dfrac{2}{{3.5}}\) và \(\dfrac{1}{3} - \dfrac{1}{5}\)
b) Tính nhanh tổng \(S,\) với \(S = \dfrac{2}{{3.5}} + \dfrac{2}{{5.7}} + \dfrac{2}{{7.9}} + ... + \dfrac{2}{{2017.2019}}\)
Tải về
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Hình nào sau đây không có trục đối xứng?
A. Hình chữ nhật B. Hình ngôi sao vàng 5 cánh
C. Hình thoi D. Hình thang có hai cạnh bên không bằng nhau
Câu 2. Câu nào đúng?
A. Góc lớn hơn góc vuông là góc tù.
B. Góc nhỏ hơn góc bẹt là góc tù.
C. Góc lớn hơn góc nhọn là góc tù.
D. Góc lớn hơn góc vuông, nhỏ hơn góc bẹt là góc tù
Câu 3. Bảng thống kê về cân nặng (theo đơn vị kilogam) của 15 học sinh lớp 6 như sau:

Theo bảng thống kê trên thì số học sinh nặng 41 kilogam là:
A. 1 B. 4 C. 2 D. 3
Câu 4. Tung đồng xu một lần. Có bao nhiêu kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu?
A. 1 B. 2 C. 3 D. 4
Phần II. Tự luận
Câu 1 Thực hiện các phép tính
\(a)\,25.\left( { - 27} \right).4\) \(b)\, - 51 + 24:\left( { - 4} \right) - 37.{\left( { - 2} \right)^2}\)
\(c)\,\dfrac{{19}}{{12}} - \dfrac{7}{{22}}:\dfrac{{21}}{{11}}\) \(d)\,\dfrac{5}{9}.\dfrac{7}{{13}} - \dfrac{5}{9}.\dfrac{3}{{13}} + \dfrac{5}{{13}}.\dfrac{{61}}{9}\)
Câu 2
1) Tìm \(x\), biết:
\(a)\,5x + 12 = 2\) \(b)\dfrac{2}{3}x - \dfrac{1}{2} = \dfrac{1}{{10}}\)
2) Tìm các giá trị nguyên của \(n\) để \(n + 8\) chia hết cho \(n + 7\)
Câu 3
1) Một lớp học có 48 học sinh gồm 3 loại : Giỏi, Khá, Trung bình. Học sinh trung bình chiếm \(\dfrac{5}{{12}}\) số học sinh cả lớp. Số học sinh khá bằng \(\dfrac{4}{7}\) số học sinh còn lại.
a) Tìm số học sinh mỗi loại của lớp?
b) Tính tỉ số phần trăm số học sinh giỏi so với số học sinh cả lớp?
2) Hai người cùng làm một công việc.Nếu làm riêng, người thứ nhất phải mất 4 giờ, người thứ hai 3 giờ. Hỏi nếu làm chung thì một giờ cả hai người làm được mấy phần công việc?
Câu 4 Trên tia Ox, vẽ các điểm A,B sao cho \(OA = 6cm,OB = 4cm\).
a) Tính độ dài đoạn thẳng AB.
b) Vẽ điểm \(C\) là trung điểm AB, điểm \(D\) là trung điểm OA. Tính độ dài đoạn thẳng CD.
Câu 5
a) So sánh: \(\dfrac{2}{{3.5}}\) và \(\dfrac{1}{3} - \dfrac{1}{5}\)
b) Tính nhanh tổng \(S,\) với \(S = \dfrac{2}{{3.5}} + \dfrac{2}{{5.7}} + \dfrac{2}{{7.9}} + ... + \dfrac{2}{{2017.2019}}\)
Phần I: Trắc nghiệm
1. D | 2. D | 3. D | 4. B |
Câu 1
Phương pháp:
Vẽ các hình đề bài cho và tìm trục đối xứng của mỗi hình.
Cách giải:
Hình chữ nhật, hình thoi, hình sao vàng 5 cánh đều là những hình có trục đối xứng.
Hình thang cân có trục đối xứng, còn hình thang có hai cạnh bên không bằng nhau sẽ không có trục đối xứng.
ChọnD.
Câu 2
Phương pháp:
Phân loại góc.
Cách giải:
- Góc lớn hơn góc vuông là góc tù hoặc góc bẹt.
- Góc nhỏ hơn góc bẹt là góc tù, góc vuông hoặc góc nhọn.
- Góc lớn hơn góc nhọn là góc tù, góc vuông hoặc góc bẹt.
- Góc lớn hơn góc vuông và nhỏ hơn góc bẹt là góc tù
Chọn D.
Câu 3
Phương pháp:
Tìm cột cân nặng 41 kg và đối chiếu số học sinh.
Cách giải:
Dựa vào bảng thống kê ta thấy có 3 học sinh nặng 41 kilogam.
Chọn D.
Câu 4
Phương pháp:
Liệt kê các khả năng có thể xảy ra.
Cách giải:
Tung đồng xu một lần thì có 2 kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là sấp hoặc ngửa.
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp:
a) Áp dụng tính chất giao hoán và kết hợp của phép nhân, khi nhân nhiều số nguyên, ta có thể đổi chỗ hoặc nhóm các phân số lại theo bất cứ cách nào sao cho việc tính toán được thuận tiện.
b) Thực hiện theo thứ tự thực hiện các phép tính: lũy thừa, nhân, chia trước, cộng trừ sau.
c) Thực hiện phép chia trước, sau đó thực hiện phép trừ hai phân số.
d) Sử dụng tính chất phân phối của phép nhân với phép cộng.
\(a.b + a.c = a.\left( {b + c} \right)\)
Cách giải:
\(\begin{array}{l}a)\,25.\left( { - 27} \right).4\\ = \left( {25.4} \right).\left( { - 27} \right)\\ = 100.\left( { - 27} \right)\\ = - 2700\end{array}\) \(\begin{array}{l}b)\, - 51 + 24:\left( { - 4} \right) - 37.{\left( { - 2} \right)^2}\\ = - 51 + \left( { - 6} \right) - 37.4\\ = - 57 - 148\\ = - 205\end{array}\)
\(\begin{array}{l}c)\,\dfrac{{19}}{{12}} - \dfrac{7}{{22}}:\dfrac{{21}}{{11}}\\ = \dfrac{{19}}{{12}} - \dfrac{7}{{22}}.\dfrac{{11}}{{21}}\\ = \dfrac{{19}}{{12}} - \dfrac{1}{6}\\ = \dfrac{{19}}{{12}} - \dfrac{2}{{12}}\\ = \dfrac{{17}}{{12}}\end{array}\) \(\begin{array}{l}d)\,\dfrac{5}{9}.\dfrac{7}{{13}} - \dfrac{5}{9}.\dfrac{3}{{13}} + \dfrac{5}{{13}}.\dfrac{{61}}{9}\\ = \dfrac{5}{9}.\left( {\dfrac{7}{{13}} - \dfrac{3}{{13}} + \dfrac{{61}}{{13}}} \right)\\ = \dfrac{5}{9}.\dfrac{{65}}{{13}}\\ = \dfrac{{25}}{9}\end{array}\)
Câu 2
Phương pháp:
a) Chuyển 12 từ vế phải sang vế trái thành \( - 12\) , rồi thực hiện cộng trừ hai số nguyên khác dấu ở vế trái. Từ đó ta tìm được x dễ dàng bằng cách lấy kết quả chia cho 5.
b) Chuyển \(\dfrac{{ - 1}}{2}\) ở vế phải sang vế trái trở thành \(\dfrac{{ + 1}}{2}\) , rồi thực hiện phép cộng hai phân số khác mẫu số, rồi tìm x bằng cách lấy kết quả thu được ở bước trước chia cho \(\dfrac{2}{3}\)
2) Biến đổi \(\dfrac{{n + 8}}{{n + 7}} = 1 + \dfrac{1}{{n + 7}}\) khi đó, để \(n + 8\) chia hết cho \(n + 7\) thì \(\dfrac{1}{{n + 7}}\) là một số nguyên, hay \(n + 7\) là ước của 1.
Cách giải:
1) \(\begin{array}{l}a)\,5x + 12 = 2\\\,\,\,\,\,\,5x\,\,\,\,\,\,\,\,\,\,\, = 2 - 12\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = - \,10:5\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = - 2\end{array}\) | \(\begin{array}{l}b)\dfrac{2}{3}x - \dfrac{1}{2} = \dfrac{1}{{10}}\\\,\,\,\,\,\dfrac{2}{3}x\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{{10}} + \dfrac{1}{2}\\\,\,\,\,\,\dfrac{2}{3}x\,\,\,\,\,\,\,\,\,\, = \,\,\dfrac{6}{{10}}\\\,\,\,\,\,\dfrac{2}{3}x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{5}\\\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\, = \dfrac{3}{5}:\dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{9}{{10}}\end{array}\) |
2) Ta có: \(\dfrac{{n + 8}}{{n + 7}} = \dfrac{{n + 7 + 1}}{{n + 7}} = \dfrac{{n + 7}}{{n + 7}} + \dfrac{1}{{n + 7}} = 1 + \dfrac{1}{{n + 7}}\,\,\left( {n \ne - 7} \right)\)
Để \(n + 8\) chia hết cho \(n + 7\) thì \(n + 7\) là ước của \(1\) .
Do đó:
+) \(\begin{array}{l}n + 7 = 1\\n\,\,\,\,\,\,\,\,\, = 1 - 7\\n\,\,\,\,\,\,\,\,\, = - 6\end{array}\)
+) \(\begin{array}{l}n + 7 = - 1\\n\,\,\,\,\,\,\,\,\, = - 1 - 7\\n\,\,\,\,\,\,\,\,\, = - 8\end{array}\)
Vậy \(n = - 6;\,\,\,\,n = - 8\) thì \(n + 8\) chia hết cho \(n + 7\)
Câu 3
Phương pháp:
1) a) tính số học sinh trung bình của lớp, biết rằng số học sinh trung bình chiếm \(\dfrac{5}{{12}}\) số học sinh cả lớp.
Chú ý: Muốn tìm \(\dfrac{m}{n}\) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\,\,\,\left( {m,n \in N,\,n \ne 0} \right).\)
Tìm số học sinh khá, rồi số học sinh giỏi .
b) Tìm tỉ số phần trăm số học sinh giỏi so với số học sinh cả lớp, ta lấy số học sinh giỏi chia cho số học sinh cả lớp rồi nhân với 100, viết thêm kí hiệu % vào bên phải kết quả tìm được.
2) Tìm số phần công việc mỗi người làm được trong 1 giờ (ta lấy 1 chia cho số giờ hoàn thành công việc của từng người. Muốn biết cả hai người làm chung trong 1 giờ được bao nhiêu phần công việc, ta cộng tổng số phần công việc của mỗi người trong 1 giờ lại.
Cách giải:
1) Số học sinh trung bình là: \(\dfrac{5}{{12}}.48 = 20\) (học sinh)
Số học sinh còn lại là: \(48 - 20 = 28\) (học sinh)
a) Số học sinh khá là: \(28.\dfrac{4}{7} = 16\) (học sinh)
Số học sinh giỏi là: \(28 - 16 = 12\) (học sinh)
b) Số học sinh giỏi chiếm số phần trăm so với số học sinh cả lớp là : \(\left( {12:48} \right).100\% = 25\% \)
2) Một giờ người thứ nhất làm được là : \(\dfrac{1}{4}\) (công việc)
Một giờ người thứ hai làm được là : \(\dfrac{1}{3}\) (công việc)
Nếu làm chung, trong một giờ cả hai người làm được là : \(\dfrac{1}{4} + \dfrac{1}{3} = \dfrac{7}{{12}}\) (công việc)
Vậy nếu làm chung thì 1 giờ cả hai người làm được \(\dfrac{7}{{12}}\) công việc
Câu 4
Phương pháp:
a) Chỉ ra \(B\) nằm giữa O và A, ta có: OB + BA = OA từ đó tính được AB.
b) Tính độ dài đoạn BC và BD
Chỉ ra B nằm giữa C và D nên BD + BC = CD, từ đó tính được CD
Cách giải:
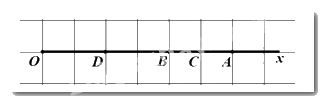
a) Trên tia \(Ox,OB < OA\left( {4cm < 6cm} \right)\) nên B nằm giữa O và A
\(\begin{array}{*{20}{l}}{ \Rightarrow OB + BA = OA}\\{ \Rightarrow 4 + BA = 6}\\{ \Rightarrow AB = 2\left( {cm} \right)}\end{array}\)
b) Vì \(C\) là trung điểm của AB nên \(CA = CB = \dfrac{1}{2}AB = 1\left( {cm} \right)\)
Vì \(D\) là trung điểm của OB nên \(DB = DO = \dfrac{1}{2}OB = 3\left( {cm} \right)\)
Vì \(B\) nằm giữa C và D nên \(BD + BC = CD \Rightarrow CD = 2 + 1 = 3\left( {cm} \right)\)
Câu 5
Phương pháp:
a) Thực hiện phép tính \(\dfrac{2}{{3.5}}\), quy đồng mẫu số hai phân số \(\dfrac{1}{3} - \dfrac{1}{5}\), rồi so sánh hai kết quả với nhau.
b) Nhận thấy:
\(\dfrac{2}{{3.5}} = \dfrac{1}{3} - \dfrac{1}{5};\,\,\,\,\,\,\,\,\dfrac{2}{{5.7}} = \dfrac{1}{5} - \dfrac{1}{7}\,\,\,\,;\,\,\,\,\,\,.....\,\,;\,\,\,\dfrac{2}{{2017.2019}} = \dfrac{1}{{2017}} - \dfrac{1}{{2019}}\)
Thay vào biểu thức của S, ta tính được tổng.
Cách giải:
a) Ta có: \(\dfrac{2}{{3.5}} = \dfrac{2}{{15}}\) và \(\dfrac{1}{3} - \dfrac{1}{5} = \dfrac{{5 - 3}}{{15}} = \dfrac{2}{{15}}\)
Vậy: \(\dfrac{2}{{3.5}} = \dfrac{1}{3} - \dfrac{1}{5}\)
b) Ta có:
\(\begin{array}{l}S = \dfrac{2}{{3.5}} + \dfrac{2}{{5.7}} + \dfrac{2}{{7.9}} + ... + \dfrac{2}{{2017.2019}}\\\,\,\,\, = \dfrac{1}{3} - \dfrac{1}{5} + \dfrac{1}{5} - \dfrac{1}{7} + \dfrac{1}{7} - \dfrac{1}{9} + ... + \dfrac{1}{{2017}} - \dfrac{1}{{2019}}\\\,\,\,\, = \dfrac{1}{3} - \dfrac{1}{{2019}}\\\,\,\,\, = \dfrac{{672}}{{2019}} = \dfrac{{224}}{{673}}\end{array}\)
Vậy \(S = \dfrac{{224}}{{673}}\)
Đề thi học kì 2 Toán 6 - Đề số 10, chương trình Chân trời sáng tạo, là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức và kỹ năng của học sinh sau một học kì học tập. Đề thi này bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, nhằm kiểm tra toàn diện các chủ đề đã được học.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để giải các bài tập này, học sinh cần nắm vững các quy tắc thực hiện các phép tính cộng, trừ, nhân, chia. Chú ý đến thứ tự thực hiện các phép tính và sử dụng các tính chất giao hoán, kết hợp để đơn giản hóa bài toán.
Ví dụ: Tính (123 + 456) x 7
Giải: (123 + 456) x 7 = 579 x 7 = 4053
Để giải các bài toán này, học sinh cần hiểu rõ khái niệm tỉ số và phần trăm, cũng như cách chuyển đổi giữa chúng. Sử dụng các công thức liên quan để tìm ra giá trị cần tính.
Ví dụ: Một cửa hàng giảm giá 10% cho một chiếc áo sơ mi có giá gốc là 200.000 đồng. Hỏi giá chiếc áo sau khi giảm giá là bao nhiêu?
Giải: Số tiền giảm giá là: 200.000 x 10% = 20.000 đồng. Giá chiếc áo sau khi giảm giá là: 200.000 - 20.000 = 180.000 đồng.
Để giải các bài tập này, học sinh cần nắm vững các khái niệm về điểm, đường thẳng, đoạn thẳng, góc, và các tính chất liên quan. Sử dụng các công cụ hình học (thước kẻ, compa, eke) để vẽ hình và tìm ra mối quan hệ giữa các yếu tố hình học.
Ví dụ: Vẽ đoạn thẳng AB dài 5cm. Vẽ trung điểm M của đoạn thẳng AB.
Giải: Sử dụng thước kẻ để vẽ đoạn thẳng AB dài 5cm. Sử dụng compa để xác định trung điểm M của đoạn thẳng AB (M là điểm cách A và B một khoảng bằng 2.5cm).
Để chuẩn bị tốt hơn cho kỳ thi, học sinh nên tham khảo thêm các tài liệu sau:
Việc luyện tập thường xuyên với các bài tập khác nhau sẽ giúp học sinh củng cố kiến thức, rèn luyện kỹ năng và tự tin hơn khi làm bài thi.
Đề thi học kì 2 Toán 6 - Đề số 10 - Chân trời sáng tạo là một cơ hội để học sinh đánh giá năng lực của bản thân và chuẩn bị cho các giai đoạn học tập tiếp theo. Chúc các em học sinh đạt kết quả tốt nhất!