Chào mừng các em học sinh đến với đề thi học kì 2 môn Toán lớp 6, đề số 5, chương trình Chân trời sáng tạo. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học và kiểm tra kết quả một cách hiệu quả.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1. A | 2. A | 3. C | 4. B |
Câu 1
Phương pháp:
Sử dụng định nghĩa tia.
Cách giải:
Có \(6\) tia: \(Ax,Bx,Ay,Cy,Az,Ez\)
Chọn A.
Câu 2
Phương pháp:
Sử dụng định nghĩa tâm đối xứng
Cách giải:
- Hình thang cân không có tâm đối xứng.
Chọn A.
Câu 3
Phương pháp:
Xác suất thực nghiệm xuất hiện sự kiện hai mặt ngửa là: Số lần xuất hiện sự kiện : Tổng số lần tung.
Cách giải:
Xác suất thực nghiệm xuất hiện sự kiện hai mặt ngửa là: \(\frac{3}{{20}}\).
Chọn C.
Câu 4
Phương pháp:
Để làm tròn số thập phân đến một hàng nào đó, ta làm như sau:
- Nếu chữ số đứng ngay bên phải hàng làm tròn nhỏ hơn 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.
- Nếu chữ số ngay bên phải hàng làm tròn lớn hơn 5 thì ta cộng thêm vào chữ số của hàng làm tròn rồi thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.
Sau đó bỏ đi những chữ số 0 ở tận cùng bên phải phần thập phân.
Cách giải:
Làm tròn số 52,0695 đến hàng trăm ta được kết quả là52,07.
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp
a) Thực hiện cộng hai phân số khác mẫu, ta quy đồng mẫu số hai phân số đó, rồi cộng tử với tử và giữ nguyên mẫu.
b) Nhận thấy số chia là một phân số có mẫu số là 10, ta chuyển \( - 1,8\) về dạng phân số có mẫu số là 10. Sau đó thự hiện chia hai phân số. Muốn chia hai phân số ta lấy số bị chia nhân với phân số nghịch đảo của số chia.
c) Sử dụng tính chất phân phối của phép nhân đối với phép cộng :
\(a.b + a.c + a.d = a.\left( {b + c + d} \right)\)
Cách giải:
\(a)\,\frac{7}{{15}} + \frac{6}{5} = \frac{7}{{15}} + \frac{{18}}{{15}} = \frac{{25}}{{15}} = \frac{5}{3}\) | \(b)\, - 1,8:\left( {1 - \frac{7}{{10}}} \right) = \frac{{ - 18}}{{10}}:\frac{3}{{10}} = \frac{{ - 18}}{{10}}.\frac{{10}}{3} = - 6\) |
\(\begin{array}{l}c)\,\frac{{ - 5}}{7}.\frac{2}{{13}} + \frac{{ - 5}}{7}.\frac{3}{{13}} - \frac{5}{7}.\frac{8}{{13}}\\\,\,\,\,\, = \frac{{ - 5}}{7}.\left( {\frac{2}{{13}} + \frac{3}{{13}} + \frac{8}{{13}}} \right)\\\,\,\,\, = \frac{{ - 5}}{7}.\,1\\\,\,\, = \frac{{ - 5}}{7}\end{array}\) |
Bài 2:
Phương pháp: a) Đổi hỗn số về phân số, rồi thực hiện quy tắc chuyển vế, chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu, rồi thực hiện phép cộng hai phân số khác mẫu, muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số của hai phân số đó rồi thực hiện cộng tử với tử, mẫu số giữ nguyên.
b) Chuyển hỗn số về phân số, rồi thực hiện chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu. Sau đó, thực hiện cộng hai phân số có cùng mẫu số (ta cộng tử với tử, giữ nguyên mẫu).
Để tìm x ta lấy kết quả cộng hai phân số chia cho \(\frac{1}{2}\).
Cách giải:
\[\begin{array}{l}a)\,x - 1\frac{2}{5} = \frac{3}{4}\\\,\,\,\,\,x\, - \,\frac{7}{5} = \frac{3}{4}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \frac{3}{4} + \frac{7}{5}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \frac{{43}}{{20}}\end{array}\] Vậy \(x = \frac{{43}}{{20}}\) | \(\begin{array}{l}b)\,\frac{1}{2}x - \frac{4}{7} = 1\frac{3}{7}\\\,\,\,\,\,\frac{1}{2}x - \frac{4}{7} = \frac{{10}}{7}\\\,\,\,\,\,\frac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \frac{{10}}{7} + \frac{4}{7}\\\,\,\,\,\,\frac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \frac{{14}}{7}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \frac{{14}}{7}:\frac{1}{2}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = 4\end{array}\) Vậy \(x = 4\) |
\[\begin{array}{l}c)\,\,\frac{2}{3}x - \frac{3}{2}\left( {x - \frac{1}{2}} \right)\,\,\,\,\,\,\, = \frac{5}{{12}}\\\,\,\,\,\,\,\frac{2}{3}x - \left( {\frac{3}{2}x - \frac{3}{2} \cdot \frac{1}{2}} \right) = \frac{5}{{12}}\\\,\,\,\,\,\,\frac{2}{3}x - \frac{3}{2}x + \frac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{ - 5}}{6}x + \frac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{5}{{12}} - \frac{3}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{ - 1}}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{ - 1}}{3}:\frac{{ - 5}}{6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\frac{2}{5}\end{array}\]
Vậy \(x = \frac{2}{5}\)
Bài 3
Phương pháp:
Áp dụng quy tắc: Muốn tìm \(\frac{m}{n}{\kern 1pt} \) của số \(b\) cho trước, ta tính \(b.\frac{m}{n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {m,n \in \mathbb{N},{\kern 1pt} {\kern 1pt} n \ne 0} \right).\)
Muốn tìm một số biết \(\frac{m}{n}{\kern 1pt} \) của nó bằng \(a\), ta tính \(a:\frac{m}{n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {m,n \in \mathbb{N},{\kern 1pt} {\kern 1pt} n \ne 0} \right).\)
Vẽ biểu đồ cột theo yêu cầu của đề bài
Cách giải:
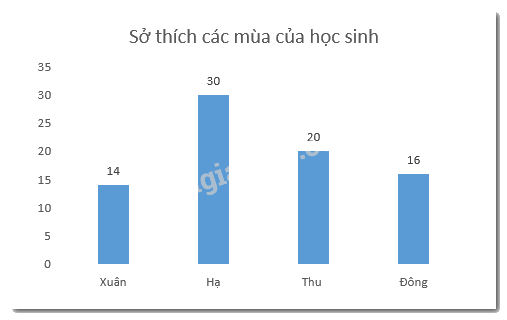
a) Tỉ lệ học sinh thích mùa xuân là: \(1 - \left( {\frac{3}{8} + \frac{1}{4} + \frac{1}{5}} \right) = 1 - \left( {\frac{{15}}{{40}} + \frac{{10}}{{40}} + \frac{8}{{40}}} \right) = \frac{7}{{40}}\)
Số học sinh tham gia khảo sát là: \(14:\frac{7}{{40}} = 14.\frac{{40}}{7} = 80\) (học sinh)
b) Số học sinh thích mùa hè là: \(80.\frac{3}{8} = 30\) (học sinh)
Số học sinh thích mùa thu là: \(80.\frac{1}{4} = 20\) (học sinh)
Số học sinh thích mùa đông là: \(80.\frac{1}{5} = 16\) (học sinh)
Biểu đồ thể hiện sở thích mùa của học sinh:
Bài 4
Phương pháp:
Nếu điểm \(C\) nằm giữa hai điểm \(A,B\) ta có: \(AC + CB = AB\)
Sử dụng tính chất trung điểm
Cách giải:
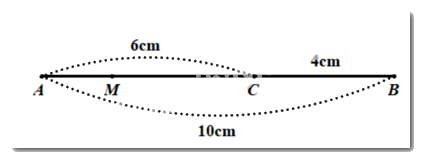
a) Vì \(C\) nằm trên đoạn thẳng \(AB\) nên \(C\) nằm giữa \(A\) và \(B\)
Suy ra \(AC + CB = AB\)
\( \Rightarrow 6 + BC = 10 \Rightarrow BC = 10 - 6 = 4\left( {cm} \right)\)
b) Vì \(C\) là trung điểm của \(BM\) nên \(CM = CB = 4\left( {cm} \right);BM = 2BC = 8\left( {cm} \right)\)
Vì \(M\) nằm giữa \(A\) và \(C\) nên \(AM + MC = AC \Rightarrow MC = 6 - 4 = 2\left( {cm} \right)\)
Bài 5
Phương pháp:
Áp dụng bất đẳng thức: \(\frac{1}{{{n^2}}} < \frac{1}{{\left( {n - 1} \right).n}}\) với \(n \in {\mathbb{N}^*},\,\,n > 1\) và đẳng thức: \(\frac{1}{{n\left( {n - 1} \right)}} = \frac{1}{{n - 1}} - \frac{1}{n}.\)
Cách giải:
Ta có :
\(\begin{array}{l}A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{2014}^2}}}\\A = \frac{1}{4} + \frac{1}{{3.3}} + \frac{1}{{4.4}} + ... + \frac{1}{{2014.2014}}\\A < \frac{1}{4} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{2013.2014}}\\A < \frac{1}{4} + \left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{{2013}} - \frac{1}{{2014}}} \right)\\A < \frac{1}{4} + \frac{1}{2} - \frac{1}{{2014}}\\A < \frac{3}{4} - \frac{1}{{2014}}\\ \Rightarrow A < \frac{3}{4}\end{array}\)
Vậy \(A < \frac{3}{4}\).
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Số tia trong hình vẽ dưới đây là:
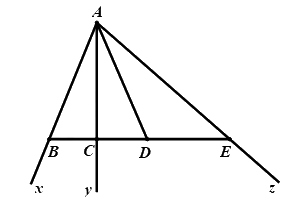
A. \(3\)tia B. \(6\) tia
C. \(4\)tia D. \(8\) tia
Câu 2: Hình thang cân có bao nhiêu tâm đối xứng?
A. 0 B. 1 C. 2 D. 3
Câu 3: Tung hai đồng xu cân đối và đồng chất 20 lần ta được kết quả như bảng dưới đây:

Xác suất thực nghiệm xuất hiện sự kiện hai mặt ngửa là:
A. \(\frac{1}{4}\) B. \(\frac{3}{5}\) C. \(\frac{3}{{20}}\) D. \(\frac{2}{5}\)
Câu 4:Làm tròn số 52,0695 đến hàng trăm ta được kết quả là:
A. 52,06 B. 52,07 C. 52,08 D. 52,89
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể) :
\(a)\,\frac{7}{{15}} + \frac{6}{5}\) \(b)\, - 1,8:\left( {1 - \frac{7}{{10}}} \right)\) \(c)\,\frac{{ - 5}}{7}.\frac{2}{{13}} + \frac{{ - 5}}{7}.\frac{3}{{13}} - \frac{5}{7}.\frac{8}{{13}}\)
Bài 2 (1,5 điểm) Tìm \(x\):
\[a)\,x - 1\frac{2}{5} = \frac{3}{4}\] \(b)\,\frac{1}{2}x - \frac{4}{7} = 1\frac{3}{7}\)
\(c)\,\,\frac{2}{3}x - \frac{3}{2}\left( {x - \frac{1}{2}} \right) = \frac{5}{{12}}\)
Bài 3 (2 điểm) Một cuộc khảo sát một số học sinh khối 6 chỉ ra rằng có \(\frac{3}{8}\) số học sinh thích mùa hè, \(\frac{1}{4}\) số học sinh thích mùa thu, \(\frac{1}{5}\) số học sịnh thích mùa đông và 14 học sinh còn lại thích mùa xuân.
a) Hãy tính số học sinh tham gia khảo sát.
b) Hãy vẽ biểu đồ cột thể hiện sở thích các mùa của học sinh.
Bài 4: (2 điểm) Cho đoạn thẳng \(AB = 10cm\). Trên đoạn thẳng \(AB\), lấy điểm \(C\) sao cho \(AC = 6cm\).
a) Tính độ dài \(BC\);
b) Lấy điểm \(M\) nằm giữa \(A\) và \(C\) sao cho \(C\) là trung điểm của \(BM\). Tính độ dài đoạn thẳng \(MC\) và \(MB\).
Bài 5:(0,5 điểm)Cho \(A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{2014}^2}}}\). Chứng tỏ: \(A < \frac{3}{4}\).
Tải về
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Số tia trong hình vẽ dưới đây là:
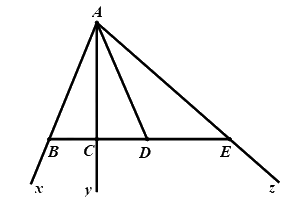
A. \(3\)tia B. \(6\) tia
C. \(4\)tia D. \(8\) tia
Câu 2: Hình thang cân có bao nhiêu tâm đối xứng?
A. 0 B. 1 C. 2 D. 3
Câu 3: Tung hai đồng xu cân đối và đồng chất 20 lần ta được kết quả như bảng dưới đây:

Xác suất thực nghiệm xuất hiện sự kiện hai mặt ngửa là:
A. \(\frac{1}{4}\) B. \(\frac{3}{5}\) C. \(\frac{3}{{20}}\) D. \(\frac{2}{5}\)
Câu 4:Làm tròn số 52,0695 đến hàng trăm ta được kết quả là:
A. 52,06 B. 52,07 C. 52,08 D. 52,89
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể) :
\(a)\,\frac{7}{{15}} + \frac{6}{5}\) \(b)\, - 1,8:\left( {1 - \frac{7}{{10}}} \right)\) \(c)\,\frac{{ - 5}}{7}.\frac{2}{{13}} + \frac{{ - 5}}{7}.\frac{3}{{13}} - \frac{5}{7}.\frac{8}{{13}}\)
Bài 2 (1,5 điểm) Tìm \(x\):
\[a)\,x - 1\frac{2}{5} = \frac{3}{4}\] \(b)\,\frac{1}{2}x - \frac{4}{7} = 1\frac{3}{7}\)
\(c)\,\,\frac{2}{3}x - \frac{3}{2}\left( {x - \frac{1}{2}} \right) = \frac{5}{{12}}\)
Bài 3 (2 điểm) Một cuộc khảo sát một số học sinh khối 6 chỉ ra rằng có \(\frac{3}{8}\) số học sinh thích mùa hè, \(\frac{1}{4}\) số học sinh thích mùa thu, \(\frac{1}{5}\) số học sịnh thích mùa đông và 14 học sinh còn lại thích mùa xuân.
a) Hãy tính số học sinh tham gia khảo sát.
b) Hãy vẽ biểu đồ cột thể hiện sở thích các mùa của học sinh.
Bài 4: (2 điểm) Cho đoạn thẳng \(AB = 10cm\). Trên đoạn thẳng \(AB\), lấy điểm \(C\) sao cho \(AC = 6cm\).
a) Tính độ dài \(BC\);
b) Lấy điểm \(M\) nằm giữa \(A\) và \(C\) sao cho \(C\) là trung điểm của \(BM\). Tính độ dài đoạn thẳng \(MC\) và \(MB\).
Bài 5:(0,5 điểm)Cho \(A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{2014}^2}}}\). Chứng tỏ: \(A < \frac{3}{4}\).
Phần I: Trắc nghiệm
1. A | 2. A | 3. C | 4. B |
Câu 1
Phương pháp:
Sử dụng định nghĩa tia.
Cách giải:
Có \(6\) tia: \(Ax,Bx,Ay,Cy,Az,Ez\)
Chọn A.
Câu 2
Phương pháp:
Sử dụng định nghĩa tâm đối xứng
Cách giải:
- Hình thang cân không có tâm đối xứng.
Chọn A.
Câu 3
Phương pháp:
Xác suất thực nghiệm xuất hiện sự kiện hai mặt ngửa là: Số lần xuất hiện sự kiện : Tổng số lần tung.
Cách giải:
Xác suất thực nghiệm xuất hiện sự kiện hai mặt ngửa là: \(\frac{3}{{20}}\).
Chọn C.
Câu 4
Phương pháp:
Để làm tròn số thập phân đến một hàng nào đó, ta làm như sau:
- Nếu chữ số đứng ngay bên phải hàng làm tròn nhỏ hơn 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.
- Nếu chữ số ngay bên phải hàng làm tròn lớn hơn 5 thì ta cộng thêm vào chữ số của hàng làm tròn rồi thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.
Sau đó bỏ đi những chữ số 0 ở tận cùng bên phải phần thập phân.
Cách giải:
Làm tròn số 52,0695 đến hàng trăm ta được kết quả là52,07.
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp
a) Thực hiện cộng hai phân số khác mẫu, ta quy đồng mẫu số hai phân số đó, rồi cộng tử với tử và giữ nguyên mẫu.
b) Nhận thấy số chia là một phân số có mẫu số là 10, ta chuyển \( - 1,8\) về dạng phân số có mẫu số là 10. Sau đó thự hiện chia hai phân số. Muốn chia hai phân số ta lấy số bị chia nhân với phân số nghịch đảo của số chia.
c) Sử dụng tính chất phân phối của phép nhân đối với phép cộng :
\(a.b + a.c + a.d = a.\left( {b + c + d} \right)\)
Cách giải:
\(a)\,\frac{7}{{15}} + \frac{6}{5} = \frac{7}{{15}} + \frac{{18}}{{15}} = \frac{{25}}{{15}} = \frac{5}{3}\) | \(b)\, - 1,8:\left( {1 - \frac{7}{{10}}} \right) = \frac{{ - 18}}{{10}}:\frac{3}{{10}} = \frac{{ - 18}}{{10}}.\frac{{10}}{3} = - 6\) |
\(\begin{array}{l}c)\,\frac{{ - 5}}{7}.\frac{2}{{13}} + \frac{{ - 5}}{7}.\frac{3}{{13}} - \frac{5}{7}.\frac{8}{{13}}\\\,\,\,\,\, = \frac{{ - 5}}{7}.\left( {\frac{2}{{13}} + \frac{3}{{13}} + \frac{8}{{13}}} \right)\\\,\,\,\, = \frac{{ - 5}}{7}.\,1\\\,\,\, = \frac{{ - 5}}{7}\end{array}\) |
Bài 2:
Phương pháp: a) Đổi hỗn số về phân số, rồi thực hiện quy tắc chuyển vế, chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu, rồi thực hiện phép cộng hai phân số khác mẫu, muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số của hai phân số đó rồi thực hiện cộng tử với tử, mẫu số giữ nguyên.
b) Chuyển hỗn số về phân số, rồi thực hiện chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu. Sau đó, thực hiện cộng hai phân số có cùng mẫu số (ta cộng tử với tử, giữ nguyên mẫu).
Để tìm x ta lấy kết quả cộng hai phân số chia cho \(\frac{1}{2}\).
Cách giải:
\[\begin{array}{l}a)\,x - 1\frac{2}{5} = \frac{3}{4}\\\,\,\,\,\,x\, - \,\frac{7}{5} = \frac{3}{4}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \frac{3}{4} + \frac{7}{5}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \frac{{43}}{{20}}\end{array}\] Vậy \(x = \frac{{43}}{{20}}\) | \(\begin{array}{l}b)\,\frac{1}{2}x - \frac{4}{7} = 1\frac{3}{7}\\\,\,\,\,\,\frac{1}{2}x - \frac{4}{7} = \frac{{10}}{7}\\\,\,\,\,\,\frac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \frac{{10}}{7} + \frac{4}{7}\\\,\,\,\,\,\frac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \frac{{14}}{7}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \frac{{14}}{7}:\frac{1}{2}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = 4\end{array}\) Vậy \(x = 4\) |
\[\begin{array}{l}c)\,\,\frac{2}{3}x - \frac{3}{2}\left( {x - \frac{1}{2}} \right)\,\,\,\,\,\,\, = \frac{5}{{12}}\\\,\,\,\,\,\,\frac{2}{3}x - \left( {\frac{3}{2}x - \frac{3}{2} \cdot \frac{1}{2}} \right) = \frac{5}{{12}}\\\,\,\,\,\,\,\frac{2}{3}x - \frac{3}{2}x + \frac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{ - 5}}{6}x + \frac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{5}{{12}} - \frac{3}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{ - 1}}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{ - 1}}{3}:\frac{{ - 5}}{6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\frac{2}{5}\end{array}\]
Vậy \(x = \frac{2}{5}\)
Bài 3
Phương pháp:
Áp dụng quy tắc: Muốn tìm \(\frac{m}{n}{\kern 1pt} \) của số \(b\) cho trước, ta tính \(b.\frac{m}{n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {m,n \in \mathbb{N},{\kern 1pt} {\kern 1pt} n \ne 0} \right).\)
Muốn tìm một số biết \(\frac{m}{n}{\kern 1pt} \) của nó bằng \(a\), ta tính \(a:\frac{m}{n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {m,n \in \mathbb{N},{\kern 1pt} {\kern 1pt} n \ne 0} \right).\)
Vẽ biểu đồ cột theo yêu cầu của đề bài
Cách giải:
a) Tỉ lệ học sinh thích mùa xuân là: \(1 - \left( {\frac{3}{8} + \frac{1}{4} + \frac{1}{5}} \right) = 1 - \left( {\frac{{15}}{{40}} + \frac{{10}}{{40}} + \frac{8}{{40}}} \right) = \frac{7}{{40}}\)
Số học sinh tham gia khảo sát là: \(14:\frac{7}{{40}} = 14.\frac{{40}}{7} = 80\) (học sinh)
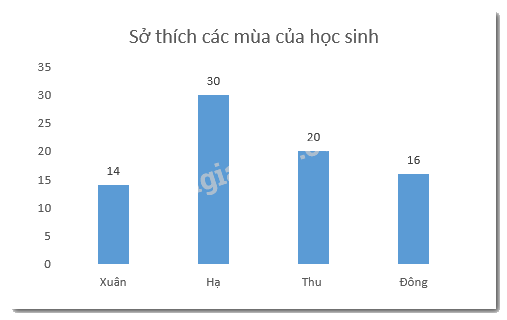
b) Số học sinh thích mùa hè là: \(80.\frac{3}{8} = 30\) (học sinh)
Số học sinh thích mùa thu là: \(80.\frac{1}{4} = 20\) (học sinh)
Số học sinh thích mùa đông là: \(80.\frac{1}{5} = 16\) (học sinh)
Biểu đồ thể hiện sở thích mùa của học sinh:
Bài 4
Phương pháp:
Nếu điểm \(C\) nằm giữa hai điểm \(A,B\) ta có: \(AC + CB = AB\)
Sử dụng tính chất trung điểm
Cách giải:
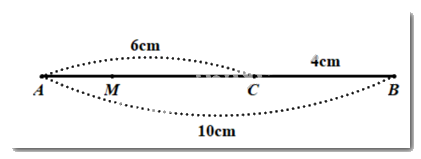
a) Vì \(C\) nằm trên đoạn thẳng \(AB\) nên \(C\) nằm giữa \(A\) và \(B\)
Suy ra \(AC + CB = AB\)
\( \Rightarrow 6 + BC = 10 \Rightarrow BC = 10 - 6 = 4\left( {cm} \right)\)
b) Vì \(C\) là trung điểm của \(BM\) nên \(CM = CB = 4\left( {cm} \right);BM = 2BC = 8\left( {cm} \right)\)
Vì \(M\) nằm giữa \(A\) và \(C\) nên \(AM + MC = AC \Rightarrow MC = 6 - 4 = 2\left( {cm} \right)\)
Bài 5
Phương pháp:
Áp dụng bất đẳng thức: \(\frac{1}{{{n^2}}} < \frac{1}{{\left( {n - 1} \right).n}}\) với \(n \in {\mathbb{N}^*},\,\,n > 1\) và đẳng thức: \(\frac{1}{{n\left( {n - 1} \right)}} = \frac{1}{{n - 1}} - \frac{1}{n}.\)
Cách giải:
Ta có :
\(\begin{array}{l}A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{2014}^2}}}\\A = \frac{1}{4} + \frac{1}{{3.3}} + \frac{1}{{4.4}} + ... + \frac{1}{{2014.2014}}\\A < \frac{1}{4} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{2013.2014}}\\A < \frac{1}{4} + \left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{{2013}} - \frac{1}{{2014}}} \right)\\A < \frac{1}{4} + \frac{1}{2} - \frac{1}{{2014}}\\A < \frac{3}{4} - \frac{1}{{2014}}\\ \Rightarrow A < \frac{3}{4}\end{array}\)
Vậy \(A < \frac{3}{4}\).
Đề thi học kì 2 Toán 6 - Đề số 5, chương trình Chân trời sáng tạo, là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong suốt học kì. Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, tập trung vào các chủ đề chính như số tự nhiên, số nguyên, phân số, tỉ số, phần trăm, hình học cơ bản và biểu thức đại số đơn giản.
Thông thường, đề thi học kì 2 Toán 6 - Đề số 5 sẽ bao gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi học kì 2 Toán 6 - Đề số 5, chương trình Chân trời sáng tạo:
Các bài tập về số tự nhiên thường tập trung vào các phép tính cộng, trừ, nhân, chia, tìm ước, bội, phân tích ra thừa số nguyên tố. Đối với số nguyên, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số nguyên, so sánh số nguyên và biểu diễn số nguyên trên trục số.
Phần này thường bao gồm các bài tập về rút gọn phân số, quy đồng mẫu số, so sánh phân số, thực hiện các phép tính cộng, trừ, nhân, chia phân số. Ngoài ra, học sinh cần nắm vững các khái niệm về phân số tối giản, phân số bằng nhau.
Các bài tập về tỉ số thường yêu cầu học sinh tìm tỉ số của hai đại lượng, giải bài toán về tỉ lệ. Phần trăm được ứng dụng trong các bài toán tính phần trăm của một số, tìm một số khi biết phần trăm của nó, tính lãi suất, giảm giá.
Phần hình học thường bao gồm các bài tập về nhận biết các hình cơ bản như điểm, đường thẳng, đoạn thẳng, góc, tam giác, tứ giác. Học sinh cần nắm vững các tính chất của các hình này và biết cách tính chu vi, diện tích của một số hình đơn giản.
Học sinh sẽ được làm quen với các biểu thức đại số đơn giản, cách thay số vào biểu thức để tính giá trị của nó. Ngoài ra, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép tính trong biểu thức.
Để giải tốt đề thi học kì 2 Toán 6 - Đề số 5, chương trình Chân trời sáng tạo, học sinh cần:
Việc ôn tập kỹ lưỡng trước khi thi là rất quan trọng. Học sinh nên dành thời gian để xem lại các bài giảng, bài tập đã học, làm các đề thi thử và tìm hiểu các dạng bài tập thường gặp. Điều này sẽ giúp học sinh tự tin hơn khi bước vào phòng thi và đạt kết quả tốt nhất.
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, đề thi và đáp án chi tiết cho học sinh các cấp. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn sẽ giúp học sinh học toán một cách hiệu quả và thú vị.
Đề thi học kì 2 Toán 6 - Đề số 5 - Chân trời sáng tạo là một cơ hội để học sinh thể hiện những kiến thức và kỹ năng đã học trong suốt học kì. Bằng việc ôn tập kỹ lưỡng và luyện tập thường xuyên, các em sẽ tự tin vượt qua bài thi và đạt kết quả tốt nhất. Chúc các em thành công!