Chào mừng các em học sinh đến với bài trắc nghiệm Toán 7 Bài 4: Định lí và chứng minh một định lí, thuộc chương trình Chân trời sáng tạo. Bài trắc nghiệm này được thiết kế để giúp các em củng cố kiến thức đã học, rèn luyện kỹ năng giải bài tập và chuẩn bị tốt nhất cho các bài kiểm tra sắp tới.
Giaitoan.edu.vn cung cấp bộ câu hỏi trắc nghiệm đa dạng, bao gồm nhiều mức độ khó khác nhau, cùng với đáp án chi tiết và lời giải thích rõ ràng.
Chọn câu đúng.
Giả thiết của định lý là điều cho biết.
Kết luận của định lý là điều được suy ra.
Giả thiết của định lý là điều được suy ra.
Cả A, B đều đúng.
Định lý sau được phát biểu thành lời là:
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
Cả A, B, C đều sai.
Phát biểu định lý sau bằng lời:
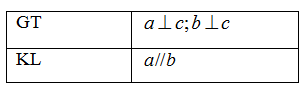
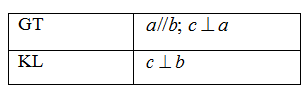
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
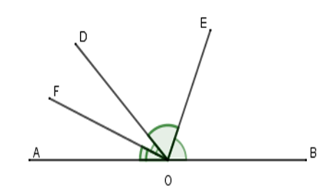
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
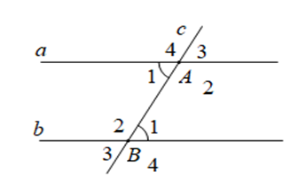
\(a//b;\,a \bot c\)
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
\(a//b;\,a//c\)
\(a//b,\) \(c\) bất kì.
Trong các câu sau, câu nào cho một định lí
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Chứng minh định lý là
Dùng lập luận để từ giả thiết suy ra kết luận
Dùng hình vẽ để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận
Cả A, B, C đều sai
Chứng minh định lý là
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
Cả A, B, C đều sai.
Trong các câu sau, câu nào không cho một định lí:
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề nhau thì có tổng số đo là 180 độ
Chọn câu sai:
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Lời giải và đáp án
Chọn câu đúng.
Giả thiết của định lý là điều cho biết.
Kết luận của định lý là điều được suy ra.
Giả thiết của định lý là điều được suy ra.
Cả A, B đều đúng.
Đáp án : D
Sử dụng lý thuyết về định lý.
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý sau được phát biểu thành lời là:
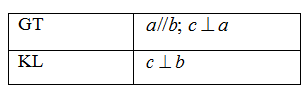
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
Cả A, B, C đều sai.
Đáp án : A
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra.
Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Phát biểu định lý sau bằng lời:
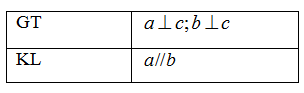
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Đáp án : C
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
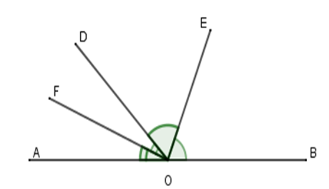
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Đáp án : A
Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
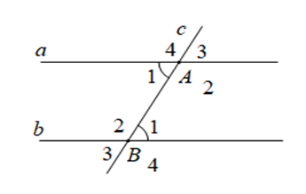
\(a//b;\,a \bot c\)
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
\(a//b;\,a//c\)
\(a//b,\) \(c\) bất kì.
Đáp án : B
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Giả thiết của định lý trên là \(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
Trong các câu sau, câu nào cho một định lí
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Đáp án : A
Sử dụng lý thuyết về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
Chứng minh định lý là
Dùng lập luận để từ giả thiết suy ra kết luận
Dùng hình vẽ để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận
Cả A, B, C đều sai
Đáp án : A
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.
Chứng minh định lý là
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
Cả A, B, C đều sai.
Đáp án : A
Sử dụng định nghĩa “chứng minh định lý”.
Chứng minh định lý là dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Trong các câu sau, câu nào không cho một định lí:
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề nhau thì có tổng số đo là 180 độ
Đáp án : D
Sử dụng nhận xét về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
+ “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
+ “Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.”
+ “Hai góc đối đỉnh thì bằng nhau”
Câu D không là định lí vì khẳng định D sai
Chọn câu sai:
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Đáp án : A
Lý thuyết về định lí
Khẳng định A sai vì định lí thường được phát biểu ở dạng: “ Nếu … thì …”
Các khẳng định B,C,D đúng .
Chọn câu đúng.
Giả thiết của định lý là điều cho biết.
Kết luận của định lý là điều được suy ra.
Giả thiết của định lý là điều được suy ra.
Cả A, B đều đúng.
Định lý sau được phát biểu thành lời là:

Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
Cả A, B, C đều sai.
Phát biểu định lý sau bằng lời:
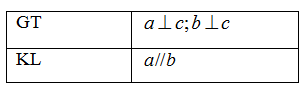
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:

Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là

\(a//b;\,a \bot c\)
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
\(a//b;\,a//c\)
\(a//b,\) \(c\) bất kì.
Trong các câu sau, câu nào cho một định lí
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Chứng minh định lý là
Dùng lập luận để từ giả thiết suy ra kết luận
Dùng hình vẽ để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận
Cả A, B, C đều sai
Chứng minh định lý là
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
Cả A, B, C đều sai.
Trong các câu sau, câu nào không cho một định lí:
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề nhau thì có tổng số đo là 180 độ
Chọn câu sai:
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Chọn câu đúng.
Giả thiết của định lý là điều cho biết.
Kết luận của định lý là điều được suy ra.
Giả thiết của định lý là điều được suy ra.
Cả A, B đều đúng.
Đáp án : D
Sử dụng lý thuyết về định lý.
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý sau được phát biểu thành lời là:

Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
Cả A, B, C đều sai.
Đáp án : A
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra.
Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Phát biểu định lý sau bằng lời:
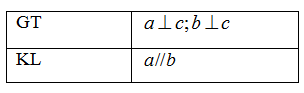
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Đáp án : C
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:

Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Đáp án : A
Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là

\(a//b;\,a \bot c\)
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
\(a//b;\,a//c\)
\(a//b,\) \(c\) bất kì.
Đáp án : B
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Giả thiết của định lý trên là \(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
Trong các câu sau, câu nào cho một định lí
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Đáp án : A
Sử dụng lý thuyết về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
Chứng minh định lý là
Dùng lập luận để từ giả thiết suy ra kết luận
Dùng hình vẽ để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận
Cả A, B, C đều sai
Đáp án : A
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.
Chứng minh định lý là
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
Cả A, B, C đều sai.
Đáp án : A
Sử dụng định nghĩa “chứng minh định lý”.
Chứng minh định lý là dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Trong các câu sau, câu nào không cho một định lí:
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề nhau thì có tổng số đo là 180 độ
Đáp án : D
Sử dụng nhận xét về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
+ “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
+ “Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.”
+ “Hai góc đối đỉnh thì bằng nhau”
Câu D không là định lí vì khẳng định D sai
Chọn câu sai:
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Đáp án : A
Lý thuyết về định lí
Khẳng định A sai vì định lí thường được phát biểu ở dạng: “ Nếu … thì …”
Các khẳng định B,C,D đúng .
Bài 4 trong chương trình Toán 7 Chân trời sáng tạo tập trung vào việc giới thiệu khái niệm định lí, các thành phần của một định lí (giả thiết, kết luận) và phương pháp chứng minh định lí. Việc nắm vững kiến thức này là nền tảng quan trọng cho việc học toán ở các lớp trên.
Một định lí là một khẳng định đúng được chứng minh bằng lý luận logic. Mỗi định lí bao gồm hai phần chính:
Ví dụ: Định lí về tổng ba góc trong một tam giác: Nếu tam giác ABC có ba góc A, B, C thì A + B + C = 180°. Trong đó, giả thiết là tam giác ABC và kết luận là tổng ba góc bằng 180°.
Chứng minh định lí là quá trình sử dụng các kiến thức, định lí đã biết, các quy tắc logic để suy luận từ giả thiết đến kết luận. Có nhiều phương pháp chứng minh định lí khác nhau, trong đó phổ biến nhất là:
Dưới đây là một số câu hỏi trắc nghiệm minh họa để các em làm quen với dạng bài tập này:
Câu 1: Trong một định lí, phần nào nêu lên điều kiện để định lí xảy ra?
Câu 2: Chọn câu trả lời đúng nhất về chứng minh định lí:
Để nắm vững kiến thức về định lí và chứng minh định lí, các em nên:
Các em có thể tìm hiểu thêm về các loại định lí khác nhau, các phương pháp chứng minh định lí phức tạp hơn và ứng dụng của định lí trong thực tế. Việc mở rộng kiến thức sẽ giúp các em hiểu sâu sắc hơn về toán học và phát triển tư duy logic.
| Tên định lí | Nội dung |
|---|---|
| Định lí về tổng ba góc trong một tam giác | Nếu tam giác ABC có ba góc A, B, C thì A + B + C = 180° |
| Định lí về góc ngoài của một tam giác | Góc ngoài tại một đỉnh của tam giác bằng tổng hai góc trong không kề với góc ngoài đó. |
Hy vọng với bài trắc nghiệm và những kiến thức được cung cấp, các em sẽ học tốt môn Toán 7 và đạt kết quả cao trong các kỳ thi sắp tới. Chúc các em thành công!