Chào mừng các em học sinh đến với bài trắc nghiệm Bài 3: Tam giác cân môn Toán 7 chương trình Chân trời sáng tạo. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức về tam giác cân, các tính chất và định lý liên quan.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, từ dễ đến khó, kèm theo đáp án chi tiết để các em tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB. Tính \(\widehat {MAN}\).
30\(^\circ \)
45\(^\circ \)
67,5\(^\circ \)
60\(^\circ \)
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Chọn khẳng định đúng nhất
Tam giác AMB đều
AM = BM = CM
AM = BC
AB + AC = BC
Cho tam giác ABC có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC.
Khẳng định đúng là:
BN = CM
BM = CN
\(\widehat {MAN} = 120^\circ \)
\(\Delta MBN = \Delta NCM\)
Phát biểu nào sau đây là đúng:
Góc ở đỉnh của một tam giác cân thì nhỏ hơn \({90^0}\)
Trong một tam giác bất kì góc lớn nhất là góc tù
Trong một tam giác vuông có thể có một góc tù
Góc ở đáy của một tam giác cân không thể là góc tù.
Một tam giác cân có góc ở đỉnh bằng \({54^0}\) thì số đo góc ở đáy là:
\({54^0}\)
\({63^0}\)
\({72^0}\)
\({90^0}\)
Để hai tam giác cân bằng nhau thì phải cần điều kiện là:
Có các cặp cạnh đáy bằng nhau
Có hai cặp cạnh bên bằng nhau
Có một cặp góc ở đỉnh và cặp cạnh đáy bằng nhau
Có một cặp góc ở đáy bằng nhau.
Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:
\(\widehat B = \widehat C\)
\(\widehat C = \frac{{{{180}^0} - \widehat A}}{2}\)
\(\widehat A = {180^0} - 2\widehat C\)
\(\widehat B \ne \widehat C\)
Lời giải và đáp án
Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB. Tính \(\widehat {MAN}\).
30\(^\circ \)
45\(^\circ \)
67,5\(^\circ \)
60\(^\circ \)
Đáp án : B
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân, tính được \(\widehat {ANM},\widehat {AMN}\) suy ra số đo góc MAN
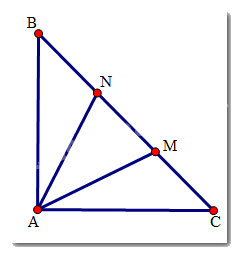
Do tam giác ABC vuông cân ở A nên \(\widehat B = \widehat C = {45^0}\).
Xét tam giác AMB có: BM = BA (gt), nên tam giác AMB cân ở B.
Do đó \(\widehat {AMB} = \frac{{{{180}^0} - \widehat B}}{2} = \frac{{{{180}^0} - {{45}^0}}}{2} = 67,5^\circ \)
Chứng minh tương tự ta được tam giác ANC cân ở C và \(\widehat {ANC} = 67,5^\circ \).
Xét tam giác AMN, ta có:
\(\widehat {MAN} = {180^0} - \left( {\widehat {AMN} + \widehat {ANM}} \right) = {180^0} - \left( {67,5^\circ + 67,5^\circ}\right) = {45^0}\).
Vậy \(\widehat {MAN} = {45^0}\)
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Chọn khẳng định đúng nhất
Tam giác AMB đều
AM = BM = CM
AM = BC
AB + AC = BC
Đáp án : B
Sử dụng các trường hợp bằng nhau của tam giác, suy ra các cạnh tương ứng bằng nhau.
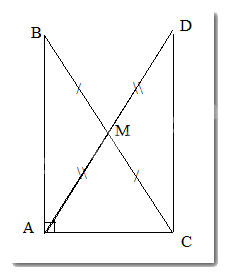
Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Khi đó, 2. AM = AD
Xét tam giác ABM và DCM, có:
AM = DM
\(\widehat {AMB} = \widehat {CMD}\) ( đối đỉnh)
BM = CM ( gt)
\( \Rightarrow \Delta ABM = \Delta DCM\) ( c.g.c)
\( \Rightarrow \widehat {ABC} = \widehat {BCD}\) (2 góc tương ứng); AB = CD ( 2 cạnh tương ứng)
Mà 2 góc ABC và BCD ở vị trí so le trong
\( \Rightarrow \)AB // CD
Mà AB \( \bot \) AC
\( \Rightarrow \) CD \( \bot \) AC ( tính chất)
Xét tam giác vuông ABC và CDA có:
AC chung
\(\widehat {BAC} = \widehat {DCA}( = 90^\circ )\)
AB = CD( cmt)
\( \Rightarrow \Delta ABC = \Delta CDA\) ( c.g.c)
\( \Rightarrow \) AD = BC ( 2 cạnh tương ứng)
\( \Rightarrow \) 2. AM = BC
\( \Rightarrow \) AM = MB = MC
Cho tam giác ABC có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC.
Khẳng định đúng là:
BN = CM
BM = CN
\(\widehat {MAN} = 120^\circ \)
\(\Delta MBN = \Delta NCM\)
Đáp án : A
Để chứng minh ai cạnh bằng nhau ta sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai cạnh tương ứng bằng nhau.
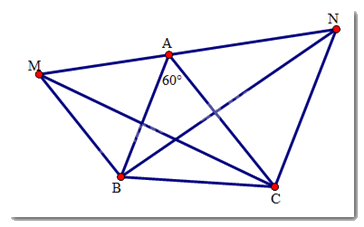
Ta có:
\(\begin{array}{l}\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\\\widehat {BAN} = \widehat {CAN} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\end{array}\)
\( \Rightarrow \)\(\widehat {MAC} = \widehat {BAN}\) .
Xét hai tam giác ABN và AMC có:
AM = AB (do tam giác AMB đều)
\(\widehat {MAC} = \widehat {BAN}\) (cmt)
AN = AC (do tam giác ANC đều)
Do đó \(\Delta ABN = \Delta AMC(c.g.c)\)
\( \Rightarrow \)BN = CM (hai cạnh tương ứng).
Phát biểu nào sau đây là đúng:
Góc ở đỉnh của một tam giác cân thì nhỏ hơn \({90^0}\)
Trong một tam giác bất kì góc lớn nhất là góc tù
Trong một tam giác vuông có thể có một góc tù
Góc ở đáy của một tam giác cân không thể là góc tù.
Đáp án : D
Sử dụng tính chất tổng ba góc của một tam giác bằng 180 độ và sử dụng tính chất tam giác cân có 2 góc ở đáy bằng nhau.
Giả sử xét trong tam giác ABC cân tại A.
Xét tam giác ABC ta có: \(\widehat A + \widehat B + \widehat C = {180^0} \Leftrightarrow \widehat B + \widehat C = {180^0} - \widehat A \Leftrightarrow \widehat C = \frac{{{{180}^0} - \widehat A}}{2}\)
Vì \(180^\circ - \widehat A < 180^\circ \Rightarrow \frac{{180^\circ - \widehat A}}{2} < \frac{{180^\circ }}{2} = 90^\circ \)
Vậy góc ở đáy của một tam giác cân không thể là góc tù.
Một tam giác cân có góc ở đỉnh bằng \({54^0}\) thì số đo góc ở đáy là:
\({54^0}\)
\({63^0}\)
\({72^0}\)
\({90^0}\)
Đáp án : B
Sử dụng tính chất tổng ba góc của một tam giác bằng 180 độ và sử dụng tính chất tam giác cân có 2 góc ở đáy bằng nhau.
Do tam giác ABC cân nên \(\widehat B = \widehat C\)
Xét tam giác ABC ta có:
\(\widehat A + \widehat B + \widehat C = {180^0} \\ \widehat B + \widehat C = {180^0} - \widehat A \\ \widehat C = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{54}^0}}}{2} = {63^0}\)
Để hai tam giác cân bằng nhau thì phải cần điều kiện là:
Có các cặp cạnh đáy bằng nhau
Có hai cặp cạnh bên bằng nhau
Có một cặp góc ở đỉnh và cặp cạnh đáy bằng nhau
Có một cặp góc ở đáy bằng nhau.
Đáp án : C
Áp dụng trường hợp bằng nhau của tam giác.
Để hai tam giác cân bằng nhau thì phải cần điều kiện là: Có một cặp góc ở đỉnh và cặp cạnh đáy bằng nhau.
Khi đó hai tam giác cân bằng nhau theo trường hợp góc – cạnh – góc.
Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:
\(\widehat B = \widehat C\)
\(\widehat C = \frac{{{{180}^0} - \widehat A}}{2}\)
\(\widehat A = {180^0} - 2\widehat C\)
\(\widehat B \ne \widehat C\)
Đáp án : D
Sử dụng tính chất tổng ba góc của một tam giác bằng 180 độ và sử dụng tính chất tam giác cân có 2 góc ở đáy bằng nhau.
Do tam giác ABC cân nên \(\widehat B = \widehat C\)
Xét tam giác ABC ta có: \(\widehat A + \widehat B + \widehat C = {180^0} \Leftrightarrow \widehat B + \widehat C = {180^0} - \widehat A \Leftrightarrow \widehat C = \frac{{{{180}^0} - \widehat A}}{2}\) hay \(\widehat A = {180^0} - 2\widehat C\)
Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB. Tính \(\widehat {MAN}\).
30\(^\circ \)
45\(^\circ \)
67,5\(^\circ \)
60\(^\circ \)
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Chọn khẳng định đúng nhất
Tam giác AMB đều
AM = BM = CM
AM = BC
AB + AC = BC
Cho tam giác ABC có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC.
Khẳng định đúng là:
BN = CM
BM = CN
\(\widehat {MAN} = 120^\circ \)
\(\Delta MBN = \Delta NCM\)
Phát biểu nào sau đây là đúng:
Góc ở đỉnh của một tam giác cân thì nhỏ hơn \({90^0}\)
Trong một tam giác bất kì góc lớn nhất là góc tù
Trong một tam giác vuông có thể có một góc tù
Góc ở đáy của một tam giác cân không thể là góc tù.
Một tam giác cân có góc ở đỉnh bằng \({54^0}\) thì số đo góc ở đáy là:
\({54^0}\)
\({63^0}\)
\({72^0}\)
\({90^0}\)
Để hai tam giác cân bằng nhau thì phải cần điều kiện là:
Có các cặp cạnh đáy bằng nhau
Có hai cặp cạnh bên bằng nhau
Có một cặp góc ở đỉnh và cặp cạnh đáy bằng nhau
Có một cặp góc ở đáy bằng nhau.
Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:
\(\widehat B = \widehat C\)
\(\widehat C = \frac{{{{180}^0} - \widehat A}}{2}\)
\(\widehat A = {180^0} - 2\widehat C\)
\(\widehat B \ne \widehat C\)
Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB. Tính \(\widehat {MAN}\).
30\(^\circ \)
45\(^\circ \)
67,5\(^\circ \)
60\(^\circ \)
Đáp án : B
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân, tính được \(\widehat {ANM},\widehat {AMN}\) suy ra số đo góc MAN

Do tam giác ABC vuông cân ở A nên \(\widehat B = \widehat C = {45^0}\).
Xét tam giác AMB có: BM = BA (gt), nên tam giác AMB cân ở B.
Do đó \(\widehat {AMB} = \frac{{{{180}^0} - \widehat B}}{2} = \frac{{{{180}^0} - {{45}^0}}}{2} = 67,5^\circ \)
Chứng minh tương tự ta được tam giác ANC cân ở C và \(\widehat {ANC} = 67,5^\circ \).
Xét tam giác AMN, ta có:
\(\widehat {MAN} = {180^0} - \left( {\widehat {AMN} + \widehat {ANM}} \right) = {180^0} - \left( {67,5^\circ + 67,5^\circ}\right) = {45^0}\).
Vậy \(\widehat {MAN} = {45^0}\)
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Chọn khẳng định đúng nhất
Tam giác AMB đều
AM = BM = CM
AM = BC
AB + AC = BC
Đáp án : B
Sử dụng các trường hợp bằng nhau của tam giác, suy ra các cạnh tương ứng bằng nhau.

Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Khi đó, 2. AM = AD
Xét tam giác ABM và DCM, có:
AM = DM
\(\widehat {AMB} = \widehat {CMD}\) ( đối đỉnh)
BM = CM ( gt)
\( \Rightarrow \Delta ABM = \Delta DCM\) ( c.g.c)
\( \Rightarrow \widehat {ABC} = \widehat {BCD}\) (2 góc tương ứng); AB = CD ( 2 cạnh tương ứng)
Mà 2 góc ABC và BCD ở vị trí so le trong
\( \Rightarrow \)AB // CD
Mà AB \( \bot \) AC
\( \Rightarrow \) CD \( \bot \) AC ( tính chất)
Xét tam giác vuông ABC và CDA có:
AC chung
\(\widehat {BAC} = \widehat {DCA}( = 90^\circ )\)
AB = CD( cmt)
\( \Rightarrow \Delta ABC = \Delta CDA\) ( c.g.c)
\( \Rightarrow \) AD = BC ( 2 cạnh tương ứng)
\( \Rightarrow \) 2. AM = BC
\( \Rightarrow \) AM = MB = MC
Cho tam giác ABC có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC.
Khẳng định đúng là:
BN = CM
BM = CN
\(\widehat {MAN} = 120^\circ \)
\(\Delta MBN = \Delta NCM\)
Đáp án : A
Để chứng minh ai cạnh bằng nhau ta sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai cạnh tương ứng bằng nhau.

Ta có:
\(\begin{array}{l}\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\\\widehat {BAN} = \widehat {CAN} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\end{array}\)
\( \Rightarrow \)\(\widehat {MAC} = \widehat {BAN}\) .
Xét hai tam giác ABN và AMC có:
AM = AB (do tam giác AMB đều)
\(\widehat {MAC} = \widehat {BAN}\) (cmt)
AN = AC (do tam giác ANC đều)
Do đó \(\Delta ABN = \Delta AMC(c.g.c)\)
\( \Rightarrow \)BN = CM (hai cạnh tương ứng).
Phát biểu nào sau đây là đúng:
Góc ở đỉnh của một tam giác cân thì nhỏ hơn \({90^0}\)
Trong một tam giác bất kì góc lớn nhất là góc tù
Trong một tam giác vuông có thể có một góc tù
Góc ở đáy của một tam giác cân không thể là góc tù.
Đáp án : D
Sử dụng tính chất tổng ba góc của một tam giác bằng 180 độ và sử dụng tính chất tam giác cân có 2 góc ở đáy bằng nhau.
Giả sử xét trong tam giác ABC cân tại A.
Xét tam giác ABC ta có: \(\widehat A + \widehat B + \widehat C = {180^0} \Leftrightarrow \widehat B + \widehat C = {180^0} - \widehat A \Leftrightarrow \widehat C = \frac{{{{180}^0} - \widehat A}}{2}\)
Vì \(180^\circ - \widehat A < 180^\circ \Rightarrow \frac{{180^\circ - \widehat A}}{2} < \frac{{180^\circ }}{2} = 90^\circ \)
Vậy góc ở đáy của một tam giác cân không thể là góc tù.
Một tam giác cân có góc ở đỉnh bằng \({54^0}\) thì số đo góc ở đáy là:
\({54^0}\)
\({63^0}\)
\({72^0}\)
\({90^0}\)
Đáp án : B
Sử dụng tính chất tổng ba góc của một tam giác bằng 180 độ và sử dụng tính chất tam giác cân có 2 góc ở đáy bằng nhau.
Do tam giác ABC cân nên \(\widehat B = \widehat C\)
Xét tam giác ABC ta có:
\(\widehat A + \widehat B + \widehat C = {180^0} \\ \widehat B + \widehat C = {180^0} - \widehat A \\ \widehat C = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{54}^0}}}{2} = {63^0}\)
Để hai tam giác cân bằng nhau thì phải cần điều kiện là:
Có các cặp cạnh đáy bằng nhau
Có hai cặp cạnh bên bằng nhau
Có một cặp góc ở đỉnh và cặp cạnh đáy bằng nhau
Có một cặp góc ở đáy bằng nhau.
Đáp án : C
Áp dụng trường hợp bằng nhau của tam giác.
Để hai tam giác cân bằng nhau thì phải cần điều kiện là: Có một cặp góc ở đỉnh và cặp cạnh đáy bằng nhau.
Khi đó hai tam giác cân bằng nhau theo trường hợp góc – cạnh – góc.
Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:
\(\widehat B = \widehat C\)
\(\widehat C = \frac{{{{180}^0} - \widehat A}}{2}\)
\(\widehat A = {180^0} - 2\widehat C\)
\(\widehat B \ne \widehat C\)
Đáp án : D
Sử dụng tính chất tổng ba góc của một tam giác bằng 180 độ và sử dụng tính chất tam giác cân có 2 góc ở đáy bằng nhau.
Do tam giác ABC cân nên \(\widehat B = \widehat C\)
Xét tam giác ABC ta có: \(\widehat A + \widehat B + \widehat C = {180^0} \Leftrightarrow \widehat B + \widehat C = {180^0} - \widehat A \Leftrightarrow \widehat C = \frac{{{{180}^0} - \widehat A}}{2}\) hay \(\widehat A = {180^0} - 2\widehat C\)
Bài 3 trong chương trình Toán 7 Chân trời sáng tạo tập trung vào việc nghiên cứu về tam giác cân. Tam giác cân là một loại tam giác đặc biệt, có hai cạnh bằng nhau. Việc hiểu rõ các tính chất và định lý liên quan đến tam giác cân là vô cùng quan trọng, không chỉ cho việc giải các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức hình học nâng cao hơn.
Ví dụ 1: Cho tam giác ABC cân tại A, có góc B = 50°. Tính góc A.
Giải: Vì tam giác ABC cân tại A nên góc B = góc C = 50°. Tổng ba góc trong một tam giác bằng 180° nên góc A = 180° - (góc B + góc C) = 180° - (50° + 50°) = 80°.
Ví dụ 2: Cho tam giác DEF cân tại D, có DE = 5cm, EF = 7cm. Tính độ dài DF.
Giải: Vì tam giác DEF cân tại D nên DE = DF = 5cm.
Để nắm vững kiến thức về tam giác cân và rèn luyện kỹ năng giải bài tập, các em nên luyện tập thêm với các bài tập khác trong sách giáo khoa, sách bài tập và các nguồn tài liệu trực tuyến khác. Giaitoan.edu.vn cung cấp một kho đề thi phong phú, đa dạng, giúp các em tự tin hơn trong các kỳ thi sắp tới.
Trắc nghiệm Bài 3: Tam giác cân Toán 7 Chân trời sáng tạo là một phần quan trọng trong chương trình học Toán 7. Việc nắm vững kiến thức và kỹ năng giải bài tập về tam giác cân sẽ giúp các em học tốt môn Toán và đạt kết quả cao trong các kỳ thi. Chúc các em học tập tốt!