Chào mừng bạn đến với bài kiểm tra trắc nghiệm về chủ đề 'Đường trung trực của một đoạn thẳng' trong chương trình Toán 7 Chân trời sáng tạo. Bài trắc nghiệm này được thiết kế để giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải bài tập.
Giaitoan.edu.vn cung cấp bộ câu hỏi đa dạng, bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp bạn tự đánh giá năng lực của mình.
Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
Hình chữ nhật
Hình vuông
Hình thoi
Hình bình hành
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
IH = IK
IH = IL
IH +IK = IL
IK = IL
Lời giải và đáp án
Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
Hình chữ nhật
Hình vuông
Hình thoi
Hình bình hành
Đáp án : C
Sử dụng tính chất đường trung trực của đoạn thẳng.
Áp dụng các trường hợp bằng nhau của tam giác suy ra các cạnh bằng nhau.
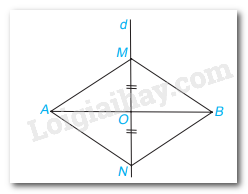
Vì M nằm trên đường trung trực của AB nên MA = MB ( tính chất)
Vì N nằm trên đường trung trực của AB nên NA = NB ( tính chất)
Xét tam giác AOM và AON có:
OM = ON
\(\widehat {AOM} = \widehat {AON}( = 90^\circ )\)
AO chung
\( \Rightarrow \Delta AOM = \Delta AON\) ( c.g.c)
\( \Rightarrow \) AM = AN ( 2 cạnh tương ứng)
Mà MA = MB; NA = NB
\( \Rightarrow \) MA = MB = NB = NA
\( \Rightarrow \) Tứ giác AMBN là hình thoi ( Tứ giác có 4 cạnh bằng nhau)
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
IH = IK
IH = IL
IH +IK = IL
IK = IL
Đáp án : A
Dựa vào tính chất tam giác cân
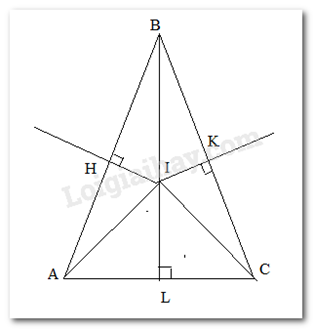
Vì tam giác ABC cân tại B nên BA = BC
Mà H, K lần lượt là trung điểm của BA và BC nên BH = BK
Xét tam giác vuộng BHI và BKI có:
BI chung
BH = BK
\( \Rightarrow BHI = \Delta BKI\) ( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \) IH = IK (hai cạnh tương ứng).
Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
Hình chữ nhật
Hình vuông
Hình thoi
Hình bình hành
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
IH = IK
IH = IL
IH +IK = IL
IK = IL
Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
Hình chữ nhật
Hình vuông
Hình thoi
Hình bình hành
Đáp án : C
Sử dụng tính chất đường trung trực của đoạn thẳng.
Áp dụng các trường hợp bằng nhau của tam giác suy ra các cạnh bằng nhau.

Vì M nằm trên đường trung trực của AB nên MA = MB ( tính chất)
Vì N nằm trên đường trung trực của AB nên NA = NB ( tính chất)
Xét tam giác AOM và AON có:
OM = ON
\(\widehat {AOM} = \widehat {AON}( = 90^\circ )\)
AO chung
\( \Rightarrow \Delta AOM = \Delta AON\) ( c.g.c)
\( \Rightarrow \) AM = AN ( 2 cạnh tương ứng)
Mà MA = MB; NA = NB
\( \Rightarrow \) MA = MB = NB = NA
\( \Rightarrow \) Tứ giác AMBN là hình thoi ( Tứ giác có 4 cạnh bằng nhau)
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
IH = IK
IH = IL
IH +IK = IL
IK = IL
Đáp án : A
Dựa vào tính chất tam giác cân

Vì tam giác ABC cân tại B nên BA = BC
Mà H, K lần lượt là trung điểm của BA và BC nên BH = BK
Xét tam giác vuộng BHI và BKI có:
BI chung
BH = BK
\( \Rightarrow BHI = \Delta BKI\) ( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \) IH = IK (hai cạnh tương ứng).
Bài 5 trong chương trình Toán 7 Chân trời sáng tạo tập trung vào khái niệm đường trung trực của một đoạn thẳng. Đây là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học, là nền tảng cho nhiều kiến thức và kỹ năng tiếp theo. Hiểu rõ về đường trung trực giúp học sinh giải quyết các bài toán liên quan đến tính chất đối xứng, khoảng cách và vị trí tương đối của các điểm.
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó. Để xác định đường trung trực, ta cần tìm trung điểm của đoạn thẳng và vẽ đường thẳng vuông góc với đoạn thẳng tại điểm đó.
Để giải các bài tập trắc nghiệm về đường trung trực, học sinh cần nắm vững định nghĩa, tính chất và các ứng dụng của đường trung trực. Ngoài ra, cần rèn luyện kỹ năng vẽ hình và phân tích đề bài một cách cẩn thận.
Ví dụ: Cho đoạn thẳng AB và điểm M là trung điểm của AB. Đường thẳng d vuông góc với AB tại M là:
Giải: Theo định nghĩa, đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó. Vậy đáp án đúng là C.
Dưới đây là một số bài tập trắc nghiệm để bạn luyện tập:
| STT | Câu hỏi | Đáp án |
|---|---|---|
| 1 | Cho đoạn thẳng CD và điểm E là trung điểm của CD. Đường thẳng d đi qua E và vuông góc với CD là... | Đường trung trực của đoạn thẳng CD |
| 2 | Điểm M nằm trên đường trung trực của đoạn thẳng AB. Vậy MA = MB là... | Đúng |
| 3 | ... | ... |
Trắc nghiệm Bài 5: Đường trung trực của một đoạn thẳng Toán 7 Chân trời sáng tạo là một phần quan trọng trong chương trình học. Việc nắm vững kiến thức và rèn luyện kỹ năng giải bài tập sẽ giúp bạn đạt kết quả tốt trong các kỳ thi và ứng dụng kiến thức vào thực tế.