Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán chương trình Cánh diều - Đề số 18.
Đề thi này được biên soạn bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Hãy tải đề thi về và tự đánh giá năng lực của mình trước khi kỳ thi học kì 1 chính thức diễn ra nhé!
Hai góc đối đỉnh thì
kề nhau.
bù nhau.
bằng nhau.
kề bù.
Số đối của \(\frac{{15}}{{16}}\) là
\(\frac{{15}}{{16}}\).
\( - \frac{{15}}{{16}}\).
\(\frac{{16}}{{15}}\).
\( - \frac{{16}}{{15}}\).
Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì
a trùng với b.
a cắt b.
\(a \bot b\).
\(a//b\).
Căn bậc hai số học của 169 là:
-13.
13.
13 và -13.
169.
Cho biết đại lượng y tỉ lệ thuận với x và khi x = 3 thì y = 9. Khi đó hệ số a của y đối với x là
3.
27.
\(\frac{1}{3}\).
\(\frac{1}{{27}}\).
Chọn khẳng định đúng:
\(\sqrt 3 \in \mathbb{N}\).
\(\sqrt 3 \in \mathbb{Z}\).
\(\frac{2}{3} \in \mathbb{Q}\).
\( - 9 \in {\mathbb{N}^*}\).
Cho \(\widehat {xOy} = 70^\circ \), tia Ot là tia phân giác của \(\widehat {xOy}\). Khi đó, số đo \(\widehat {xOt}\) bằng
\(140^\circ \).
\(70^\circ \).
\(40^\circ \).
\(35^\circ \).
Nếu \(\frac{a}{2} = \frac{b}{3}\) và \(\frac{b}{4} = \frac{c}{5}\) thì a, b, c lần lượt tỉ lệ với các số:
2; 3; 5.
8; 12; 20.
8; 12; 15.
9; 12; 15.
Trong các số sau đây, số nào là số vô tỉ?
\(\sqrt {25} \).
\(\sqrt {16} \).
\(\sqrt {17} \).
\(\sqrt 9 \).
Phát biểu nào sau đây không đúng về hình lập phương?
Có 6 mặt, 8 đỉnh và 12 cạnh.
Có 8 mặt, 6 đỉnh và 12 cạnh.
Có 4 đường chéo.
Có các cạnh đều bằng nhau.
Cho \(\left| x \right| = 4\) thì giá trị của x là:
4.
-4.
16.
-4 hoặc 4.
Bạn An làm một chiếc hộp để đựng quà sinh nhật bằng bìa cứng có dạng hình hộp chữ nhật với chiều dài 25cm, chiều rộng 20cm, chiều cao 10cm. Thể tích của chiếc hộp là
\(5000c{m^3}\).
\(900c{m^3}\).
\(4500c{m^3}\).
\(500c{m^3}\).
Thực hiện phép tính:
a) \(\sqrt 9 + \left| { - 12} \right|\)
b) \(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^7}:{\left( {\frac{1}{3}} \right)^5} - 9\)
c) \(\left( {\frac{{ - 3}}{{17}} + \frac{5}{{13}}} \right) - \left( {\frac{{14}}{{17}} - \frac{8}{{13}}} \right)\)
Tìm x, biết:
a) \(5\frac{3}{4} + \frac{1}{4}:x = 5\frac{1}{2}\)
b) \(\left| {x - \frac{3}{2}} \right| = \frac{7}{{12}}\)
Một trường THCS phân công ba lớp 7A1; 7A2; 7A3 chăm 54 cây xanh trong trường. Số cây mỗi lớp cần chăm sóc tỉ lệ thuận với số học sinh của lớp. Biết lớp 7A1 có 40 học sinh; lớp 7A2 có 32 học sinh; lớp 7A3 có 36 học sinh. Tính số cây mỗi lớp cần chăm sóc?
Bảng dữ liệu sau cho biết doanh thu trong 6 tháng cuối năm của một cửa hàng bán quần áo:

a) Em hãy vẽ biểu đồ đoạn thẳng biểu diễn dữ liệu trên.
b) Tháng nào cửa hàng có doanh thu cao nhất? Tháng nào cửa hàng có doanh thu thấp nhất?
Nhân dịp cuối năm, cửa hàng A giảm giá 30% cho tất cả các sản phẩm.
a) Biết đôi giày bạn Nam mua ở cửa hàng A có giá niêm yết là 450 000 đồng. Hỏi bạn Nam phải trả bao nhiêu tiền cho đôi giày đó? (Bạn Nam không phải là khách hàng thân thiết).b) Cửa hàng A có thêm chính sách khuyến mãi với khách hàng thân thiết được giảm thêm 5% trên giá đã giảm. Biết bạn Phúc là khách hàng thân thiết của cửa hàng A và bạn Phúc phải trả số tiền mua một cây vợt cầu lông là 399 000 đồng. Hỏi giá ban đầu của cây vợt đó là bao nhiêu?
Hai góc đối đỉnh thì
kề nhau.
bù nhau.
bằng nhau.
kề bù.
Đáp án : C
Dựa vào tính chất của hai góc đối đỉnh.
Hai góc đối đỉnh thì bằng nhau.
Đáp án C
Số đối của \(\frac{{15}}{{16}}\) là
\(\frac{{15}}{{16}}\).
\( - \frac{{15}}{{16}}\).
\(\frac{{16}}{{15}}\).
\( - \frac{{16}}{{15}}\).
Đáp án : B
Hai số đối nhau thì có tổng bằng 1.
Số đối của \(\frac{{15}}{{16}}\) là \( - \frac{{15}}{{16}}\) vì \(\frac{{15}}{{16}} + \left( { - \frac{{15}}{{16}}} \right) = 0\)
Đáp án B
Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì
a trùng với b.
a cắt b.
\(a \bot b\).
\(a//b\).
Đáp án : D
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
Nếu góc tạo thành có một cặp góc đồng vị bằng nhau thì a // b.
Đáp án D
Căn bậc hai số học của 169 là:
-13.
13.
13 và -13.
169.
Đáp án : B
Áp dụng kiến thức về căn bậc hai của một số: \(x = {a^2}\) thì \(\sqrt x = a\).
Căn bậc hai số học của 169 là \(\sqrt {169} = 13\).
Đáp án B
Cho biết đại lượng y tỉ lệ thuận với x và khi x = 3 thì y = 9. Khi đó hệ số a của y đối với x là
3.
27.
\(\frac{1}{3}\).
\(\frac{1}{{27}}\).
Đáp án : A
Hệ số tỉ lệ a của y tỉ lệ thuận với x là: \(a = \frac{y}{x}\).
Hệ số a của y đối với x là: \(a = \frac{9}{3} = 3\).
Đáp án A
Chọn khẳng định đúng:
\(\sqrt 3 \in \mathbb{N}\).
\(\sqrt 3 \in \mathbb{Z}\).
\(\frac{2}{3} \in \mathbb{Q}\).
\( - 9 \in {\mathbb{N}^*}\).
Đáp án : C
Kiểm tra xem các số có thuộc tập hợp số đó hay không.
\({\mathbb{N}^*}\) là tập hợp số tự nhiên khác 0.
\(\mathbb{N}\) là tập hợp số tự nhiên.
\(\mathbb{Z}\) là tập hợp số nguyên.
\(\mathbb{Q}\) là tập hợp số hữu tỉ.
\(\sqrt 3 \) không phải là số tự nhiên nên \(\sqrt 3 \in \mathbb{N}\) là khẳng định sai.
\(\sqrt 3 \) không phải là số nguyên nên \(\sqrt 3 \in \mathbb{Z}\) là khẳng định sai.
\(\frac{2}{3}\) là số hữu tỉ nên \(\frac{2}{3} \in \mathbb{Q}\) là khẳng định đúng.
\( - 9\) không phải là số tự nhiên nên \( - 9 \in {\mathbb{N}^*}\) là khẳng định sai.
Đáp án C
Cho \(\widehat {xOy} = 70^\circ \), tia Ot là tia phân giác của \(\widehat {xOy}\). Khi đó, số đo \(\widehat {xOt}\) bằng
\(140^\circ \).
\(70^\circ \).
\(40^\circ \).
\(35^\circ \).
Đáp án : D
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
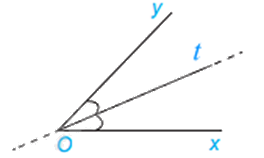
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \frac{1}{2}.70^\circ = 35^\circ \).
Đáp án D
Nếu \(\frac{a}{2} = \frac{b}{3}\) và \(\frac{b}{4} = \frac{c}{5}\) thì a, b, c lần lượt tỉ lệ với các số:
2; 3; 5.
8; 12; 20.
8; 12; 15.
9; 12; 15.
Đáp án : C
Đưa hai tỉ lệ thức về một dãy tỉ số bằng nhau.
Ta có: \(\frac{a}{2} = \frac{b}{3}\) nên \(\frac{a}{8} = \frac{b}{{12}}\)
\(\frac{b}{4} = \frac{c}{5}\) nên \(\frac{b}{{12}} = \frac{c}{{15}}\)
Suy ra \(\frac{a}{8} = \frac{b}{{12}} = \frac{c}{{15}}\).
Vậy a, b, c lần lượt tỉ lệ với các số 8; 12; 15.
Đáp án C
Trong các số sau đây, số nào là số vô tỉ?
\(\sqrt {25} \).
\(\sqrt {16} \).
\(\sqrt {17} \).
\(\sqrt 9 \).
Đáp án : C
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Số \(\sqrt {17} \) là số vô tỉ, các số còn lại là số hữu tỉ vì: \(\sqrt {25} = 5\); \(\sqrt {16} = 4\); \(\sqrt 9 = 3\).
Đáp án C
Phát biểu nào sau đây không đúng về hình lập phương?
Có 6 mặt, 8 đỉnh và 12 cạnh.
Có 8 mặt, 6 đỉnh và 12 cạnh.
Có 4 đường chéo.
Có các cạnh đều bằng nhau.
Đáp án : B
Dựa vào đặc điểm của hình lập phương.
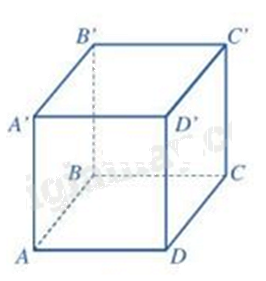
Hình lập phương có:
6 mặt, 12 cạnh và 8 đỉnh nên A đúng, B sai.
4 đường chéo nên C đúng.
các cạnh đều bằng nhau nên D đúng.
Đáp án B
Cho \(\left| x \right| = 4\) thì giá trị của x là:
4.
-4.
16.
-4 hoặc 4.
Đáp án : D
Nếu \(\left| x \right| = a\) thì \(x = a\) hoặc \(x = - a\)
Với \(\left| x \right| = 4\) thì \(x = 4\) hoặc \(x = - 4\).
Đáp án D
Bạn An làm một chiếc hộp để đựng quà sinh nhật bằng bìa cứng có dạng hình hộp chữ nhật với chiều dài 25cm, chiều rộng 20cm, chiều cao 10cm. Thể tích của chiếc hộp là
\(5000c{m^3}\).
\(900c{m^3}\).
\(4500c{m^3}\).
\(500c{m^3}\).
Đáp án : A
Thể tích của hình hộp chữ nhật là: V = chiều dài . chiều rộng . chiều cao.
Thể tích của chiếc hộp là: \(V = 25.20.10 = 5000\left( {c{m^3}} \right)\)
Đáp án A
Thực hiện phép tính:
a) \(\sqrt 9 + \left| { - 12} \right|\)
b) \(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^7}:{\left( {\frac{1}{3}} \right)^5} - 9\)
c) \(\left( {\frac{{ - 3}}{{17}} + \frac{5}{{13}}} \right) - \left( {\frac{{14}}{{17}} - \frac{8}{{13}}} \right)\)
Áp dụng thứ tự thực hiện phép tính:
* Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia, ta thực hiện các phép tính từ trái sang phải.
* Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:
Lũy thừa => Nhân và chia => Cộng và trừ
* Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau. Trường hợp có nhiều dấu ngoặc, ta thực hiện theo thứ tự ( ) => [ ] => { }
a) \(\sqrt 9 + \left| { - 12} \right| = 3 + 12 = 15\)
b) \(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^7}:{\left( {\frac{1}{3}} \right)^5} - 9\)
\(\begin{array}{l} = \frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^{7 - 5}} - 9\\ = \frac{{17}}{9} + \frac{1}{9} - 9\\ = 2 - 9 = - 7\end{array}\)
c) \(\left( {\frac{{ - 3}}{{17}} + \frac{5}{{13}}} \right) - \left( {\frac{{14}}{{17}} - \frac{8}{{13}}} \right)\)
\(\begin{array}{l} = \frac{{ - 3}}{{17}} + \frac{5}{{13}} - \frac{{14}}{{17}} + \frac{8}{{13}}\\ = \left( {\frac{{ - 3}}{{17}} - \frac{{14}}{{17}}} \right) + \left( {\frac{5}{{13}} + \frac{8}{{13}}} \right)\\ = - 1 + 1 = 0\end{array}\)
Tìm x, biết:
a) \(5\frac{3}{4} + \frac{1}{4}:x = 5\frac{1}{2}\)
b) \(\left| {x - \frac{3}{2}} \right| = \frac{7}{{12}}\)
Áp dụng quy tắc chuyển vế đổi dấu.
b) Đưa về dạng \(\left| A \right| = B\), chia hai trường hợp: A = B hoặc A = -B.
a) \(5\frac{3}{4} + \frac{1}{4}:x = 5\frac{1}{2}\)
\(\begin{array}{l}\frac{1}{4}:x = 5\frac{1}{2} - 5\frac{3}{4}\\\frac{1}{4}:x = \frac{1}{2} - \frac{3}{4}\\\frac{1}{4}:x = \frac{{ - 1}}{4}\\x = \frac{1}{4}:\frac{{ - 1}}{4}\\x = - 1\end{array}\)
Vậy \(x = - 1\)
b) \(\left| {x - \frac{3}{2}} \right| = \frac{7}{{12}}\)
\(x - \frac{3}{2} = \frac{7}{{12}}\) hoặc \(x - \frac{3}{2} = - \frac{7}{{12}}\)
\(x = \frac{7}{{12}} + \frac{3}{2}\) hoặc \(x = - \frac{7}{{12}} + \frac{3}{2}\)
\(x = \frac{{25}}{{12}}\) hoặc \(x = \frac{{11}}{{12}}\)
Vậy \(x \in \left\{ {\frac{{25}}{{12}};\frac{{11}}{{12}}} \right\}\)
Một trường THCS phân công ba lớp 7A1; 7A2; 7A3 chăm 54 cây xanh trong trường. Số cây mỗi lớp cần chăm sóc tỉ lệ thuận với số học sinh của lớp. Biết lớp 7A1 có 40 học sinh; lớp 7A2 có 32 học sinh; lớp 7A3 có 36 học sinh. Tính số cây mỗi lớp cần chăm sóc?
Gọi số cây ba lớp 7A1; 7A2; 7A3 chăm sóc lần lượt là x, y, z (cây) (\(x,y,z \in {\mathbb{N}^*}\))
Lập luận suy ra x + y + z = 54
Lập dãy tỉ số bằng nhau \(\frac{x}{{40}} = \frac{y}{{32}} = \frac{z}{{36}}\)
Áp dụng tính chất dãy tỉ số bằng nhau để tìm x, y, z.
Gọi số cây ba lớp 7A1; 7A2; 7A3 chăm sóc lần lượt là x, y, z (cây) (\(x,y,z \in {\mathbb{N}^*}\))
Vì ba lớp 7A1; 7A2; 7A3 chăm 54 cây xanh nên x + y + z = 54.
Vì số cây mỗi lớp cần chăm sóc tỉ lệ thuận với số học sinh của lớp nên ta có: \(\frac{x}{{40}} = \frac{y}{{32}} = \frac{z}{{36}}\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{40}} = \frac{y}{{32}} = \frac{z}{{36}} = \frac{{x + y + z}}{{40 + 32 + 36}} = \frac{{54}}{{108}} = 0,5\).
Suy ra x = 40.0,5 = 20; y = 32.0,5 = 16; z = 36.0,5 = 18
Vậy số cây ba lớp 7A1; 7A2; 7A3 chăm sóc lần lượt là 20; 16; 18 cây.
Bảng dữ liệu sau cho biết doanh thu trong 6 tháng cuối năm của một cửa hàng bán quần áo:

a) Em hãy vẽ biểu đồ đoạn thẳng biểu diễn dữ liệu trên.
b) Tháng nào cửa hàng có doanh thu cao nhất? Tháng nào cửa hàng có doanh thu thấp nhất?
a) Cách vẽ biểu đồ đoạn thẳng:
Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau
- Trục ngang: Ghi các mốc thời gian
- Trục dọc: Chọn khoảng chia thích hợp với số liệu và ghi số ở các vạch chia
Bước 2:
- Tại mỗi mốc thời gian trên trục ngang, đánh dấu một điểm cách điểm mốc thời gian theo chiều thẳng đứng một khoảng bằng số liệu tại mốc thời gian đó, tương ứng với khoảng chia trên trục dọc
- Vẽ các đoạn thẳng nối từng cặp điểm tương ứng với cặp mốc thời gian liên tiếp, ta được một đường gấp khúc biểu diễn sự thay đổi số liệu theo thời gian.
Bước 3: Hoàn thiện biểu đồ:
- Ghi tên biểu đồ
- Ghi chú các giá trị số liệu tại các đầu đoạn thẳng
- Ghi đơn vị trên 2 trục
b) Quan sát biểu đồ để xác định điểm biểu diễn tháng nào ở vị trí cao nhất, thấp nhất.
a) Biểu đồ đoạn thẳng:
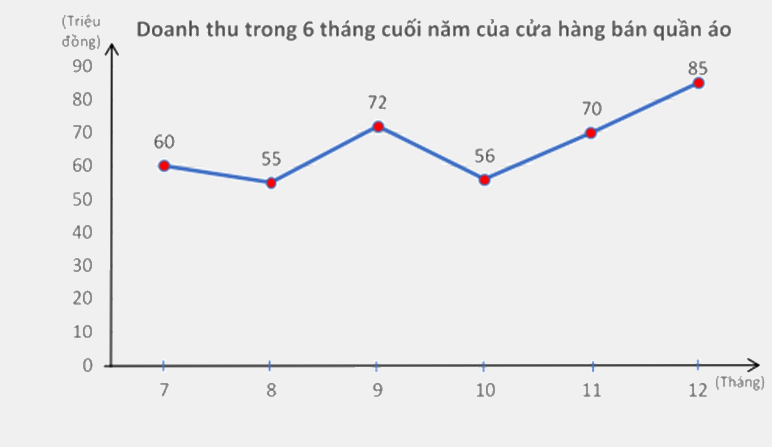
b) Tháng 12 cửa hàng có doanh thu cao nhất (85 triệu đồng).
Tháng 8 cửa hàng có doanh thu thấp nhất (55 triệu đồng).
Nhân dịp cuối năm, cửa hàng A giảm giá 30% cho tất cả các sản phẩm.
a) Biết đôi giày bạn Nam mua ở cửa hàng A có giá niêm yết là 450 000 đồng. Hỏi bạn Nam phải trả bao nhiêu tiền cho đôi giày đó? (Bạn Nam không phải là khách hàng thân thiết).b) Cửa hàng A có thêm chính sách khuyến mãi với khách hàng thân thiết được giảm thêm 5% trên giá đã giảm. Biết bạn Phúc là khách hàng thân thiết của cửa hàng A và bạn Phúc phải trả số tiền mua một cây vợt cầu lông là 399 000 đồng. Hỏi giá ban đầu của cây vợt đó là bao nhiêu?
a) Tính số tiền đôi giày được giảm.
Số tiền bạn Nam phải trả = giá đôi giày – số tiền giảm.
b) Tính giá tiền trước khi giảm 5% của khách hàng thân thiết.
Tính giá ban đầu của cây vợt.
a) Số tiền đôi giày được giảm là:
450 000 . 30% = 135 000 (đồng)
Số tiền bạn Nam phải trả cho đôi giày là:
450 000 – 135 000 = 315 000 (đồng)
b) Giá của cây vợt cầu lông trước khi được giảm giá thêm 5% là:
399 000 : (100% - 5%) = 420 000 (đồng)
Giá ban đầu của cây vợt bạn Phúc đã mua là:
420000 : (100% - 30%) = 600 000 (đồng)
Đề thi học kì 1 Toán 7 Cánh diều - Đề số 18 là một trong những đề thi quan trọng giúp học sinh lớp 7 đánh giá kiến thức đã học trong nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của toán học.
Thông thường, đề thi học kì 1 Toán 7 Cánh diều - Đề số 18 có cấu trúc gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi học kì 1 Toán 7 Cánh diều - Đề số 18:
Các bài tập về số hữu tỉ và số thực thường yêu cầu học sinh:
Các bài tập về biểu thức đại số thường yêu cầu học sinh:
Các bài tập về phương trình bậc nhất một ẩn thường yêu cầu học sinh:
Các bài tập về bất đẳng thức thường yêu cầu học sinh:
Để đạt kết quả tốt trong kỳ thi học kì 1 Toán 7 Cánh diều - Đề số 18, học sinh cần:
Ngoài việc giải đề thi, học sinh có thể tham khảo thêm các tài liệu ôn thi sau:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi học kì 1 Toán 7 Cánh diều - Đề số 18!