Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 7 - Đề số 1 - Cánh diều, một tài liệu ôn tập vô cùng quan trọng dành cho học sinh lớp 7. Đề thi được biên soạn theo chương trình sách giáo khoa Cánh diều, bao gồm các dạng bài tập thường gặp và có độ khó phù hợp.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Nếu tam giác \(ABC\) cân tại B thì
A. Đường trung tuyến AM đồng thời là đường phân giác
B. Đường trung tuyến CP đồng thời là đường trung trực
C. Đường trung tuyến BN đồng thời là đường phân giác
D. Đường trung tuyến AM đồng thời là đường trung trực
Câu 2. Cho \(\Delta ABC\) có \(\angle A = {50^0}\,,\,\angle B = {90^0}\) thì quan hệ giữa ba cạnh \(AB,AC,BC\) là:
A. \(BC > AC > AB\)
B. \(AB > BC > AC\)
C. \(AB > AC > BC\)
D. \(AC > BC > AB\)
Câu 3. Trong năm 2020, công ty chè Phú Minh thu được 25 tỉ đồng từ việc xuất khẩu chè. Biểu đồ hình quạt tròn ở hình bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các loại chè xuất khẩu trong năm 2020 của công ty Phú Minh.
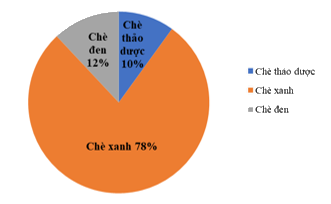
Bảng nào sau đây là bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020?
A.
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,5 | 19,1 | 3,2 |
B.
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,5 | 19,5 | 3 |
C.
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,2 | 19,2 | 3 |
D.
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,4 | 19 | 3,6 |
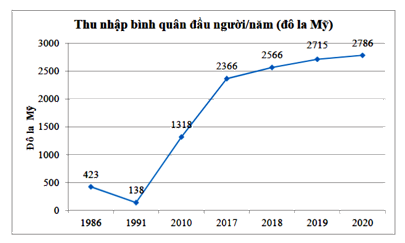
Câu 4. Biểu đồ bên dưới biểu diễn thu nhập bình quân đầu người/năm của Việt Nam (tính theo đô la Mỹ) ở một số năm trong những gia đoạn từ 1986 đến 2020. Hãy cho biết năm nào Việt Nam có thu nhập cao nhất, cụ thể là bao nhiêu đô la?
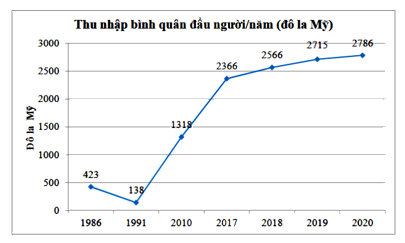
A. Năm 1991, Việt Nam có mức thu nhập thấp nhất là 138 đô la/năm.
B. Năm 2019, Việt Nam có mức thu nhập cao nhất là 2738 đô la/năm.
C. Năm 2018, Việt Nam có mức thu nhập cao nhất là 2566 đô la/năm.
D. Năm 2020, Việt Nam có mức thu nhập cao nhất là 2786 đô la/năm.
Câu 5. Biểu thức đại số biểu thị “Tổng lập phương của hai số x và y” là
A. x3 – y3;
B. x + y;
C. x3 + y3;
D. (x + y)3.
Câu 6. Hệ số cao nhất của đa thức M = 10x2 – 4x + 3 – 5x5 là
A. 10;
B. -4;
C. 3;
D. -5.
Câu 7. Cho tam giác ABC, đường trung tuyến AM = 9 cm. Gọi G là trọng tâm của tam giác. Tính độ dài GM?
A. GM = 6 cm;
B. GM = 9 cm;
C. GM = 3 cm;
D. GM = 18 cm.
Câu 8. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?
A. 8cm; 9cm; 10cm;
B. 3cm; 4cm; 5cm;
C. 1cm; 2cm; 3cm;
D. 11cm; 9cm; 7cm.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1 điểm) Tìm \(x\) biết:
a) \(\dfrac{1}{{12}} + x = \dfrac{{ - 11}}{{12}}\)
b) \(\dfrac{{2x - 1}}{{27}} = \dfrac{3}{{2x - 1}}\)
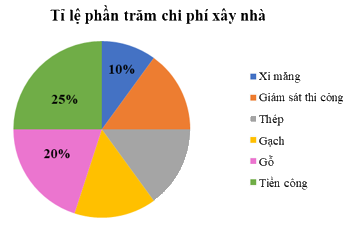
Bài 2. (1 điểm) Chi phí xây dựng nhà được biểu diễn qua biểu đồ hình quạt tròn sau:
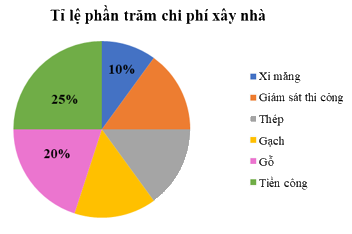
a) Tính số phần trăm chi phí gạch. Biết rằng chi phí giám sát thi công, thép, gạch bằng nhau.
b) Biết rằng để xây dựng một ngôi nhà bác An đã chi trả hết 2,5 tỉ đồng. Hỏi chi phí trả tiền công là bao nhiêu?
Bài 3. (2 điểm) Cho các đa thức:
\(A\left( x \right) = 2\,{x^4} - 5\,{x^3} + 7\,x - 5 + 4\,{x^3} + 3\,{x^2} + 2\,x + 3\)
\(B\left( x \right) = 5\,{x^4} - 3\,{x^3} + 5\,x - 3\,{x^4} - 2\,{x^3}\, + 9 - 6\,x\)
\(C\left( x \right) = {x^4} + 4\,{x^2} + 5\)
a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),\,B\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Bài 4. (3,5 điểm) Cho \(\Delta ABC\) vuông tại \(A\) có \(\angle C = {30^0},\) đường cao \(AH.\) Trên đoạn \(HC\) lấy điểm \(D\) sao cho \(HD = HB.\)
a) Chứng minh \(\Delta AHB = \Delta AHD\).
b) Chứng minh \(\Delta ABD\) là tam giác đều.
c) Từ \(C\) kẻ \(CE\) vuông góc với đường thẳng \(AD\)\(\left( {E \in \,AD} \right)\). Chứng minh \(DE = HB\).
d) Từ \(D\) kẻ \(DF\) vuông góc với \(AC\) (\(F\,\)thuộc \(AC\)), \(I\) là giao điểm của \(CE\) và \(AH.\) Chứng minh ba điểm \(I,\,D,\,F\) thẳng hàng.
Bài 5. (0,5 điểm)
Cho \(a,b,c\) là các số thực khác không \(\left( {b \ne c} \right)\) và \(\dfrac{1}{c} = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right)\). Chứng minh rằng: \(\dfrac{a}{b} = \dfrac{{a - c}}{{c - b}}\).
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Nếu tam giác \(ABC\) cân tại B thì
A. Đường trung tuyến AM đồng thời là đường phân giác
B. Đường trung tuyến CP đồng thời là đường trung trực
C. Đường trung tuyến BN đồng thời là đường phân giác
D. Đường trung tuyến AM đồng thời là đường trung trực
Câu 2. Cho \(\Delta ABC\) có \(\angle A = {50^0}\,,\,\angle B = {90^0}\) thì quan hệ giữa ba cạnh \(AB,AC,BC\) là:
A. \(BC > AC > AB\)
B. \(AB > BC > AC\)
C. \(AB > AC > BC\)
D. \(AC > BC > AB\)
Câu 3. Trong năm 2020, công ty chè Phú Minh thu được 25 tỉ đồng từ việc xuất khẩu chè. Biểu đồ hình quạt tròn ở hình bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các loại chè xuất khẩu trong năm 2020 của công ty Phú Minh.
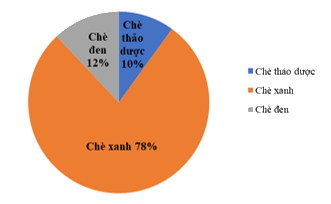
Bảng nào sau đây là bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020?
A.
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,5 | 19,1 | 3,2 |
B.
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,5 | 19,5 | 3 |
C.
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,2 | 19,2 | 3 |
D.
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,4 | 19 | 3,6 |
Câu 4. Biểu đồ bên dưới biểu diễn thu nhập bình quân đầu người/năm của Việt Nam (tính theo đô la Mỹ) ở một số năm trong những gia đoạn từ 1986 đến 2020. Hãy cho biết năm nào Việt Nam có thu nhập cao nhất, cụ thể là bao nhiêu đô la?
A. Năm 1991, Việt Nam có mức thu nhập thấp nhất là 138 đô la/năm.
B. Năm 2019, Việt Nam có mức thu nhập cao nhất là 2738 đô la/năm.
C. Năm 2018, Việt Nam có mức thu nhập cao nhất là 2566 đô la/năm.
D. Năm 2020, Việt Nam có mức thu nhập cao nhất là 2786 đô la/năm.
Câu 5. Biểu thức đại số biểu thị “Tổng lập phương của hai số x và y” là
A. x3 – y3;
B. x + y;
C. x3 + y3;
D. (x + y)3.
Câu 6. Hệ số cao nhất của đa thức M = 10x2 – 4x + 3 – 5x5 là
A. 10;
B. -4;
C. 3;
D. -5.
Câu 7. Cho tam giác ABC, đường trung tuyến AM = 9 cm. Gọi G là trọng tâm của tam giác. Tính độ dài GM?
A. GM = 6 cm;
B. GM = 9 cm;
C. GM = 3 cm;
D. GM = 18 cm.
Câu 8. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?
A. 8cm; 9cm; 10cm;
B. 3cm; 4cm; 5cm;
C. 1cm; 2cm; 3cm;
D. 11cm; 9cm; 7cm.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1 điểm) Tìm \(x\) biết:
a) \(\dfrac{1}{{12}} + x = \dfrac{{ - 11}}{{12}}\)
b) \(\dfrac{{2x - 1}}{{27}} = \dfrac{3}{{2x - 1}}\)
Bài 2. (1 điểm) Chi phí xây dựng nhà được biểu diễn qua biểu đồ hình quạt tròn sau:
a) Tính số phần trăm chi phí gạch. Biết rằng chi phí giám sát thi công, thép, gạch bằng nhau.
b) Biết rằng để xây dựng một ngôi nhà bác An đã chi trả hết 2,5 tỉ đồng. Hỏi chi phí trả tiền công là bao nhiêu?
Bài 3. (2 điểm) Cho các đa thức:
\(A\left( x \right) = 2\,{x^4} - 5\,{x^3} + 7\,x - 5 + 4\,{x^3} + 3\,{x^2} + 2\,x + 3\)
\(B\left( x \right) = 5\,{x^4} - 3\,{x^3} + 5\,x - 3\,{x^4} - 2\,{x^3}\, + 9 - 6\,x\)
\(C\left( x \right) = {x^4} + 4\,{x^2} + 5\)
a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),\,B\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Bài 4. (3,5 điểm) Cho \(\Delta ABC\) vuông tại \(A\) có \(\angle C = {30^0},\) đường cao \(AH.\) Trên đoạn \(HC\) lấy điểm \(D\) sao cho \(HD = HB.\)
a) Chứng minh \(\Delta AHB = \Delta AHD\).
b) Chứng minh \(\Delta ABD\) là tam giác đều.
c) Từ \(C\) kẻ \(CE\) vuông góc với đường thẳng \(AD\)\(\left( {E \in \,AD} \right)\). Chứng minh \(DE = HB\).
d) Từ \(D\) kẻ \(DF\) vuông góc với \(AC\) (\(F\,\)thuộc \(AC\)), \(I\) là giao điểm của \(CE\) và \(AH.\) Chứng minh ba điểm \(I,\,D,\,F\) thẳng hàng.
Bài 5. (0,5 điểm)
Cho \(a,b,c\) là các số thực khác không \(\left( {b \ne c} \right)\) và \(\dfrac{1}{c} = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right)\). Chứng minh rằng: \(\dfrac{a}{b} = \dfrac{{a - c}}{{c - b}}\).
I. Trắc nghiệm:
1. C | 2. D | 3. B | 4. D |
5. C | 6. D | 7. C | 8. C |
Câu 1:
Phương pháp:
Trong tam giác cân, đường trung tuyến ứng với đỉnh cân đồng thời là đường trung trực, đường cao, đường phân giác.
Cách giải:
Tam giác ABC cân tại B nên đường trung tuyến BN đồng thời là đường phân giác.
Chọn C.
Câu 2:
Phương pháp: Dựa vào mối quan hệ giữa góc và cạnh trong tam giác để so sánh các cạnh với nhau.
Cách giải:
Ta có: \(\angle C = {180^0} - \left( {{{50}^0} + {{90}^0}} \right) = {40^0}\).
\( \Rightarrow \angle C < \angle A < \angle B\)
\( \Rightarrow AB < BC < AC\) hay \(AC > BC > AB\).
Chọn D.
Câu 3:
Phương pháp:
Đọc và mô tả dữ liệu của biểu đồ hình quạt tròn.
Số tiền thu được tương ứng = % tương ứng . toàn bộ số tiền thu được
Cách giải:
Số tiền công ty Phú Minh thu được từ chè thảo dược là: \(10\% .25 = 2,5\) (tỉ đồng)
Số tiền công ty Phú Minh thu được từ chè xanh là: \(78\% .25 = 19,5\) (tỉ đồng)
Số tiền công ty Phú Minh thu được từ chè đen là: \(12\% .25 = 3\) (tỉ đồng)
Ta có bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020:
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,5 | 19,5 | 3 |
Chọn B.
Câu 4:
Phương pháp:
Phân tích dữ liệu biểu đồ đoạn thẳng.
Cách giải:
Từ biểu đồ đoạn thẳng, ta thấy năm 2020, Việt Nam có mức thu nhập cao nhất là 2786 đô la/năm.
Chọn D.
Câu 5:
Phương pháp:
Mô tả
Cách giải:
Tổng lập phương của hai số x và y là x3 + y3
Câu 6:
Phương pháp:
Hệ số cao nhất của đa thức là hệ số của hạng tử có bậc cao nhất trong đa thức.
Cách giải:
Đa thức M = 10x2 – 4x + 3 – 5x5 có hệ số cao nhất là -5.
Chọn D
Chú ý: Hệ số cao nhất không phải hệ số lớn nhất trong đa thức.
Câu 7:
Phương pháp: Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM\).
Cách giải:
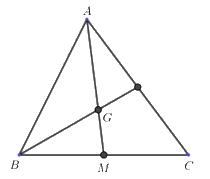
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(GM = \dfrac{1}{3}AM = \dfrac{1}{3}.9 = 3(cm)\).
Chọn C.
Câu 8:
Phương pháp: Bất đẳng thức tam giác: Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu không thì bộ 3 độ dài đó không tạo được thành tam giác.
Cách giải:
Vì 1 + 2 = 3 nên không thỏa mãn bất đẳng thức tam giác.
Chọn C.
II. TỰ LUẬN
Bài 1:
Phương pháp:
a) Thực hiện các phép toán với phân số.
b) Vận dụng định nghĩa hai phân số bằng nhau: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(ad = bc\).
Cách giải:
a) \(\dfrac{1}{{12}} + x = \dfrac{{ - 11}}{{12}}\)
\(\begin{array}{l}x = \dfrac{{ - 11}}{{12}} - \dfrac{1}{{12}}\\x = \dfrac{{ - 11 - 1}}{{12}}\\x = \dfrac{{ - 12}}{{12}} = - 1\end{array}\)
Vậy phương trình có nghiệm là \(x = - 1\)
b) \(\dfrac{{2x - 1}}{{27}} = \dfrac{3}{{2x - 1}}\)
\(\begin{array}{l}{\left( {2x - 1} \right)^2} = 27.3 = 81\\{\left( {2x - 1} \right)^2} = {\left( { \pm 9} \right)^2}\end{array}\)
Trường hợp 1: \(\begin{array}{l}2x - 1 = 9\\2x = 10\\x = 5\end{array}\) | Trường hợp 2: \(\begin{array}{l}2x - 1 = - 9\\2x = - 8\\x = - 4\end{array}\) |
Vậy phương trình có nghiệm là \(x = 5\) hoặc \(x = - 4\)
Bài 2:
Phương pháp:
a) Tính tổng số phần trăm chi phí các nguyên vật liệu còn lại, suy ra số phần trăm chi phí gạch.
b) Số tiền công = 25% tổng số tiền
Cách giải:
a) Tổng số phần trăm chi phí giám sát thi công, thép và gạch là: 100% - 20% - 25% - 10% = 45%
Vì chi phí giám sát thi công, thép, gạch bằng nhau nên số phần trăm chi phí gạch là: 45% : 3 = 15%
b) Chi phí trả tiền công là: 25%.2,5 = 0,625 (tỉ đồng)
Bài 3:
Phương pháp:
a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),\,B\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Cách giải:
a) Thu gọn:
\(\begin{array}{l}A\left( x \right) = 2\,{x^4} - 5\,{x^3} + 7\,x - 5 + 4\,{x^3} + 3\,{x^2} + 2\,x + 3\\A\left( x \right) = 2\,{x^4} + \left( { - 5\,{x^3} + 4\,{x^3}} \right) + 3{x^2} + \left( {7\,x + 2\,x} \right) - 5 + 3\\A\left( x \right) = 2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x\, - 2\end{array}\)
\(\begin{array}{l}B\left( x \right) = 5\,{x^4} - 3\,{x^3} + 5\,x - 3\,{x^4} - 2\,{x^3}\, + 9 - 6\,x\\B\left( x \right) = \left( {5\,{x^4} - 3\,{x^4}} \right) + \left( { - 3\,{x^3} - 2\,{x^3}} \right) + \left( {5\,x - 6\,x} \right) + 9\\B\left( x \right) = \,\,\,\,\,\,2\,{x^4}\, - \,5{x^3} - x + 9\end{array}\)
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
\(\begin{array}{l} + )\,A\left( x \right) + B\left( x \right) = \left( {2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x - 2} \right) + \left( {2\,{x^4} - 5\,{x^3} - x + 9} \right)\\ = \left( {2\,{x^4} + 2\,{x^4}} \right) + \left( { - {x^3} - 5\,{x^3}} \right) + 3\,{x^2} + \left( {9\,x - x} \right) + \left( { - 2 + 9} \right)\\ = \,\,\,4\,{x^4} - 6\,{x^3} + 3\,{x^2} + 8\,x + 7\end{array}\)
\(\begin{array}{l} + )\,A\left( x \right) - B\left( x \right) = \left( {2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x - 2} \right) - \left( {2\,{x^4} - 5\,{x^3} - x + 9} \right)\\ = \left( {2\,{x^4} - \,{x^3} + 3\,{x^2} + 9\,x - 2} \right) - 2\,{x^4} + 5\,{x^3} + x - 9\\ = \left( {2\,{x^4} - \,2\,{x^4}} \right) + \left( { - {x^3} + 5\,{x^3}} \right) + 3\,{x^2} + \left( {9\,x + x} \right) + \left( { - 2 - 9} \right)\\ = \,\,\,\,\,\,\,\,\,\,4\,{x^3} + \,3\,{x^2} + 10\,x - 11\end{array}\)
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Ta có: \(C\left( x \right) = {x^4} + 4\,{x^2} + 5\).
Vì \({x^4}\, > 0,\,\,\forall \,x\) và \({x^2} > 0,\,\forall \,x\) nên \(C\left( x \right) > 0,\,\,\forall \,x.\)
\( \Rightarrow \) không có giá trị nào của \(x\) làm cho \(C\left( x \right) = 0\).
\( \Rightarrow \,C\left( x \right)\) là đa thức không có nghiệm.
Bài 4: Phương pháp:
a) Chứng minh hai tam giác bằng nhau theo trường hợp c.g.c.
b) Chứng minh \(\Delta ABD\)là tam giác cân có một góc bằng \({60^0}\), rồi suy ra \(\Delta ABD\) là tam giác đều.
c) Chứng minh \(DE = DH\) (hai cạnh tương ứng). Mà \(DH = DB\) (giả thiết) \( \Rightarrow DE = DB\).
d) Chứng minh DF và IF cùng vuông góc với AC nên DI trùng với DF hay I, D, F thẳng hàng.
Cách giải:
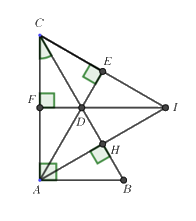
a) Xét \(\Delta AHB\) và \(\Delta AHD\) ta có:
\(HD = HB\) (gt)
\(AH\,\,chung\)
\(\angle AHB = \angle AHD = {90^0}\)\( \Rightarrow \)\(\Delta AHB = \,\Delta AHD\) (c.g.c)
b) \(\Delta ABC\) vuông tại \(A\),
có \(\angle C = {30^0} \Rightarrow \angle B = {90^0} - {30^0} = {60^0}\) (định lý tổng ba góc của một tam giác).
Vì \(\Delta AHB = \,\Delta AHD\) (cmt)
\( \Rightarrow AB = AD\) (hai cạnh tương ứng).
\( \Rightarrow \Delta ABD\) cân tại \(A\) mà \(\angle B = {60^0}\)
Do đó: \(\Delta ABD\)là tam giác đều.
c) Vì \(\Delta ABD\)là tam giác đều (cmt)
\( \Rightarrow \angle DAB = {60^0}\)
\(\begin{array}{l} \Rightarrow \angle CAD = {90^0} - \angle DAB\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {90^0} - {60^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {30^0}\end{array}\)
Xét \(\Delta ACD\) có \(\angle ACD = \angle \,CAD = {30^0}\).
\( \Rightarrow \Delta ACD\) cân tại \(D.\)
\( \Rightarrow \,CD = AD\)
Xét \(\Delta DEC\) và \(\Delta DHA\) có:
\(CD = AD\,\,\left( {cmt} \right)\)
\(\angle E = \angle H = {90^0}\)
\(\angle CDE = \angle ADH\) (đối đỉnh)
\( \Rightarrow \,\Delta DEC = \Delta DHA\) (cạnh huyền – góc nhọn).
\( \Rightarrow DE = DH\) (hai cạnh tương ứng).
Mà \(DH = DB\) (giả thiết)
\( \Rightarrow DE = DB\).
d) Xét \(\Delta CED\) và \(\Delta AHD\) có:
HD = HB (gt)
Mà DE = BH nên DE = DH.
\(\Delta CED = \Delta AHD\) (cạnh góc vuông - góc nhọn)
suy ra CE = AH, CD = DA, \(\widehat{DCE} = \widehat{DAH}\)
Vì CD = DA nên tam giác CDA cân, do đó \(\widehat{DCF} = \widehat{DAF}\)
Xét tam giác CDF và tam giác ADF có:
CD = AD
FD chung
\(\widehat{CFD} = \widehat{AFD} (=90^\circ)\)
nên \(\Delta CDF = \Delta ADF\) (cạnh huyền - cạnh góc vuông)
suy ra CF = FA.
Suy ra \(\widehat{DCE}+\widehat{DCF} = \widehat{DAH}+\widehat{DAF}\)
hay \(\widehat{ECF} = \widehat{HAF}\)
Suy ra tam giác ACI cân tại I.
Suy ra \(CI = IA\)
Xét tam giác CIF và tam giác AIF có:
CI = AI (cmt)
IF chung
CF = FA (cmt)
suy ra \(\Delta CIF = \Delta AIF\) (c.c.c)
suy ra \(\widehat{CFI} = \widehat{AFI}\)
Mà hai góc này là hai góc kề bù nên \(\widehat{CFI} = \widehat{AFI} = \frac{180^\circ}{2} = 90^\circ\) hay \(IF \bot CA\)
Mà \(DF \bot AC\) nên DF và IF trùng nhau, hay I, D, F thẳng hàng.
Câu 5:
Phương pháp:
Vận dụng định nghĩa hai phân số bằng nhau để chứng minh.
Cách giải:
Ta có: \(\dfrac{1}{c} = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{1}{c} = \dfrac{{a + b}}{{2ab}}\\ \Rightarrow 2ab = ac + bc\\ \Rightarrow ab + ab = ac + bc\\ \Rightarrow ab - bc = ac - ab\\ \Rightarrow b\left( {a - c} \right) = a\left( {c - b} \right)\end{array}\)
\( \Rightarrow \dfrac{a}{b} = \dfrac{{a - c}}{{c - b}}\) (đpcm)
I. Trắc nghiệm:
1. C | 2. D | 3. B | 4. D |
5. C | 6. D | 7. C | 8. C |
Câu 1:
Phương pháp:
Trong tam giác cân, đường trung tuyến ứng với đỉnh cân đồng thời là đường trung trực, đường cao, đường phân giác.
Cách giải:
Tam giác ABC cân tại B nên đường trung tuyến BN đồng thời là đường phân giác.
Chọn C.
Câu 2:
Phương pháp: Dựa vào mối quan hệ giữa góc và cạnh trong tam giác để so sánh các cạnh với nhau.
Cách giải:
Ta có: \(\angle C = {180^0} - \left( {{{50}^0} + {{90}^0}} \right) = {40^0}\).
\( \Rightarrow \angle C < \angle A < \angle B\)
\( \Rightarrow AB < BC < AC\) hay \(AC > BC > AB\).
Chọn D.
Câu 3:
Phương pháp:
Đọc và mô tả dữ liệu của biểu đồ hình quạt tròn.
Số tiền thu được tương ứng = % tương ứng . toàn bộ số tiền thu được
Cách giải:
Số tiền công ty Phú Minh thu được từ chè thảo dược là: \(10\% .25 = 2,5\) (tỉ đồng)
Số tiền công ty Phú Minh thu được từ chè xanh là: \(78\% .25 = 19,5\) (tỉ đồng)
Số tiền công ty Phú Minh thu được từ chè đen là: \(12\% .25 = 3\) (tỉ đồng)
Ta có bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020:
Loại chè | Chè thảo dược | Chè xanh | Chè đen |
Số tiền (tỉ đồng) | 2,5 | 19,5 | 3 |
Chọn B.
Câu 4:
Phương pháp:
Phân tích dữ liệu biểu đồ đoạn thẳng.
Cách giải:
Từ biểu đồ đoạn thẳng, ta thấy năm 2020, Việt Nam có mức thu nhập cao nhất là 2786 đô la/năm.
Chọn D.
Câu 5:
Phương pháp:
Mô tả
Cách giải:
Tổng lập phương của hai số x và y là x3 + y3
Câu 6:
Phương pháp:
Hệ số cao nhất của đa thức là hệ số của hạng tử có bậc cao nhất trong đa thức.
Cách giải:
Đa thức M = 10x2 – 4x + 3 – 5x5 có hệ số cao nhất là -5.
Chọn D
Chú ý: Hệ số cao nhất không phải hệ số lớn nhất trong đa thức.
Câu 7:
Phương pháp: Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM\).
Cách giải:
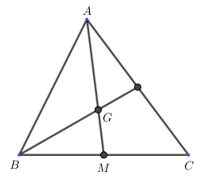
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(GM = \dfrac{1}{3}AM = \dfrac{1}{3}.9 = 3(cm)\).
Chọn C.
Câu 8:
Phương pháp: Bất đẳng thức tam giác: Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu không thì bộ 3 độ dài đó không tạo được thành tam giác.
Cách giải:
Vì 1 + 2 = 3 nên không thỏa mãn bất đẳng thức tam giác.
Chọn C.
II. TỰ LUẬN
Bài 1:
Phương pháp:
a) Thực hiện các phép toán với phân số.
b) Vận dụng định nghĩa hai phân số bằng nhau: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(ad = bc\).
Cách giải:
a) \(\dfrac{1}{{12}} + x = \dfrac{{ - 11}}{{12}}\)
\(\begin{array}{l}x = \dfrac{{ - 11}}{{12}} - \dfrac{1}{{12}}\\x = \dfrac{{ - 11 - 1}}{{12}}\\x = \dfrac{{ - 12}}{{12}} = - 1\end{array}\)
Vậy phương trình có nghiệm là \(x = - 1\)
b) \(\dfrac{{2x - 1}}{{27}} = \dfrac{3}{{2x - 1}}\)
\(\begin{array}{l}{\left( {2x - 1} \right)^2} = 27.3 = 81\\{\left( {2x - 1} \right)^2} = {\left( { \pm 9} \right)^2}\end{array}\)
Trường hợp 1: \(\begin{array}{l}2x - 1 = 9\\2x = 10\\x = 5\end{array}\) | Trường hợp 2: \(\begin{array}{l}2x - 1 = - 9\\2x = - 8\\x = - 4\end{array}\) |
Vậy phương trình có nghiệm là \(x = 5\) hoặc \(x = - 4\)
Bài 2:
Phương pháp:
a) Tính tổng số phần trăm chi phí các nguyên vật liệu còn lại, suy ra số phần trăm chi phí gạch.
b) Số tiền công = 25% tổng số tiền
Cách giải:
a) Tổng số phần trăm chi phí giám sát thi công, thép và gạch là: 100% - 20% - 25% - 10% = 45%
Vì chi phí giám sát thi công, thép, gạch bằng nhau nên số phần trăm chi phí gạch là: 45% : 3 = 15%
b) Chi phí trả tiền công là: 25%.2,5 = 0,625 (tỉ đồng)
Bài 3:
Phương pháp:
a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),\,B\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Cách giải:
a) Thu gọn:
\(\begin{array}{l}A\left( x \right) = 2\,{x^4} - 5\,{x^3} + 7\,x - 5 + 4\,{x^3} + 3\,{x^2} + 2\,x + 3\\A\left( x \right) = 2\,{x^4} + \left( { - 5\,{x^3} + 4\,{x^3}} \right) + 3{x^2} + \left( {7\,x + 2\,x} \right) - 5 + 3\\A\left( x \right) = 2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x\, - 2\end{array}\)
\(\begin{array}{l}B\left( x \right) = 5\,{x^4} - 3\,{x^3} + 5\,x - 3\,{x^4} - 2\,{x^3}\, + 9 - 6\,x\\B\left( x \right) = \left( {5\,{x^4} - 3\,{x^4}} \right) + \left( { - 3\,{x^3} - 2\,{x^3}} \right) + \left( {5\,x - 6\,x} \right) + 9\\B\left( x \right) = \,\,\,\,\,\,2\,{x^4}\, - \,5{x^3} - x + 9\end{array}\)
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
\(\begin{array}{l} + )\,A\left( x \right) + B\left( x \right) = \left( {2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x - 2} \right) + \left( {2\,{x^4} - 5\,{x^3} - x + 9} \right)\\ = \left( {2\,{x^4} + 2\,{x^4}} \right) + \left( { - {x^3} - 5\,{x^3}} \right) + 3\,{x^2} + \left( {9\,x - x} \right) + \left( { - 2 + 9} \right)\\ = \,\,\,4\,{x^4} - 6\,{x^3} + 3\,{x^2} + 8\,x + 7\end{array}\)
\(\begin{array}{l} + )\,A\left( x \right) - B\left( x \right) = \left( {2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x - 2} \right) - \left( {2\,{x^4} - 5\,{x^3} - x + 9} \right)\\ = \left( {2\,{x^4} - \,{x^3} + 3\,{x^2} + 9\,x - 2} \right) - 2\,{x^4} + 5\,{x^3} + x - 9\\ = \left( {2\,{x^4} - \,2\,{x^4}} \right) + \left( { - {x^3} + 5\,{x^3}} \right) + 3\,{x^2} + \left( {9\,x + x} \right) + \left( { - 2 - 9} \right)\\ = \,\,\,\,\,\,\,\,\,\,4\,{x^3} + \,3\,{x^2} + 10\,x - 11\end{array}\)
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Ta có: \(C\left( x \right) = {x^4} + 4\,{x^2} + 5\).
Vì \({x^4}\, > 0,\,\,\forall \,x\) và \({x^2} > 0,\,\forall \,x\) nên \(C\left( x \right) > 0,\,\,\forall \,x.\)
\( \Rightarrow \) không có giá trị nào của \(x\) làm cho \(C\left( x \right) = 0\).
\( \Rightarrow \,C\left( x \right)\) là đa thức không có nghiệm.
Bài 4: Phương pháp:
a) Chứng minh hai tam giác bằng nhau theo trường hợp c.g.c.
b) Chứng minh \(\Delta ABD\)là tam giác cân có một góc bằng \({60^0}\), rồi suy ra \(\Delta ABD\) là tam giác đều.
c) Chứng minh \(DE = DH\) (hai cạnh tương ứng). Mà \(DH = DB\) (giả thiết) \( \Rightarrow DE = DB\).
d) Chứng minh DF và IF cùng vuông góc với AC nên DI trùng với DF hay I, D, F thẳng hàng.
Cách giải:
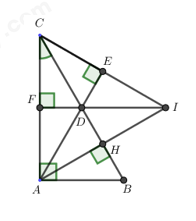
a) Xét \(\Delta AHB\) và \(\Delta AHD\) ta có:
\(HD = HB\) (gt)
\(AH\,\,chung\)
\(\angle AHB = \angle AHD = {90^0}\)\( \Rightarrow \)\(\Delta AHB = \,\Delta AHD\) (c.g.c)
b) \(\Delta ABC\) vuông tại \(A\),
có \(\angle C = {30^0} \Rightarrow \angle B = {90^0} - {30^0} = {60^0}\) (định lý tổng ba góc của một tam giác).
Vì \(\Delta AHB = \,\Delta AHD\) (cmt)
\( \Rightarrow AB = AD\) (hai cạnh tương ứng).
\( \Rightarrow \Delta ABD\) cân tại \(A\) mà \(\angle B = {60^0}\)
Do đó: \(\Delta ABD\)là tam giác đều.
c) Vì \(\Delta ABD\)là tam giác đều (cmt)
\( \Rightarrow \angle DAB = {60^0}\)
\(\begin{array}{l} \Rightarrow \angle CAD = {90^0} - \angle DAB\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {90^0} - {60^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {30^0}\end{array}\)
Xét \(\Delta ACD\) có \(\angle ACD = \angle \,CAD = {30^0}\).
\( \Rightarrow \Delta ACD\) cân tại \(D.\)
\( \Rightarrow \,CD = AD\)
Xét \(\Delta DEC\) và \(\Delta DHA\) có:
\(CD = AD\,\,\left( {cmt} \right)\)
\(\angle E = \angle H = {90^0}\)
\(\angle CDE = \angle ADH\) (đối đỉnh)
\( \Rightarrow \,\Delta DEC = \Delta DHA\) (cạnh huyền – góc nhọn).
\( \Rightarrow DE = DH\) (hai cạnh tương ứng).
Mà \(DH = DB\) (giả thiết)
\( \Rightarrow DE = DB\).
d) Xét \(\Delta CED\) và \(\Delta AHD\) có:
HD = HB (gt)
Mà DE = BH nên DE = DH.
\(\Delta CED = \Delta AHD\) (cạnh góc vuông - góc nhọn)
suy ra CE = AH, CD = DA, \(\widehat{DCE} = \widehat{DAH}\)
Vì CD = DA nên tam giác CDA cân, do đó \(\widehat{DCF} = \widehat{DAF}\)
Xét tam giác CDF và tam giác ADF có:
CD = AD
FD chung
\(\widehat{CFD} = \widehat{AFD} (=90^\circ)\)
nên \(\Delta CDF = \Delta ADF\) (cạnh huyền - cạnh góc vuông)
suy ra CF = FA.
Suy ra \(\widehat{DCE}+\widehat{DCF} = \widehat{DAH}+\widehat{DAF}\)
hay \(\widehat{ECF} = \widehat{HAF}\)
Suy ra tam giác ACI cân tại I.
Suy ra \(CI = IA\)
Xét tam giác CIF và tam giác AIF có:
CI = AI (cmt)
IF chung
CF = FA (cmt)
suy ra \(\Delta CIF = \Delta AIF\) (c.c.c)
suy ra \(\widehat{CFI} = \widehat{AFI}\)
Mà hai góc này là hai góc kề bù nên \(\widehat{CFI} = \widehat{AFI} = \frac{180^\circ}{2} = 90^\circ\) hay \(IF \bot CA\)
Mà \(DF \bot AC\) nên DF và IF trùng nhau, hay I, D, F thẳng hàng.
Câu 5:
Phương pháp:
Vận dụng định nghĩa hai phân số bằng nhau để chứng minh.
Cách giải:
Ta có: \(\dfrac{1}{c} = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{1}{c} = \dfrac{{a + b}}{{2ab}}\\ \Rightarrow 2ab = ac + bc\\ \Rightarrow ab + ab = ac + bc\\ \Rightarrow ab - bc = ac - ab\\ \Rightarrow b\left( {a - c} \right) = a\left( {c - b} \right)\end{array}\)
\( \Rightarrow \dfrac{a}{b} = \dfrac{{a - c}}{{c - b}}\) (đpcm)
Đề thi giữa kì 2 Toán 7 - Đề số 1 - Cánh diều là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức của học sinh sau nửa học kỳ 2. Đề thi bao gồm các chủ đề chính như biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức, hàm số và đồ thị, các yếu tố hình học cơ bản.
Thông thường, đề thi giữa kì 2 Toán 7 - Cánh diều có cấu trúc gồm:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 2 Toán 7 - Cánh diều:
Các bài tập về thu gọn biểu thức, tìm giá trị của biểu thức, chứng minh đẳng thức. Ví dụ:
Thu gọn biểu thức: 3x + 2y - x + 5y
Tìm giá trị của biểu thức A = 2x2 - 3x + 1 khi x = -1
Các bài tập về giải phương trình, tìm nghiệm của phương trình, ứng dụng phương trình để giải bài toán thực tế. Ví dụ:
Giải phương trình: 2x - 5 = 7
Tìm x sao cho 3(x + 2) = 15
Các bài tập về giải bất đẳng thức, so sánh các số, tìm tập nghiệm của bất đẳng thức. Ví dụ:
Giải bất đẳng thức: x + 3 > 5
So sánh hai số: 2x + 1 và 3x - 2 (với x > 1)
Các bài tập về xác định hàm số, vẽ đồ thị hàm số, tìm giá trị của hàm số tại một điểm. Ví dụ:
Hàm số y = 2x + 1 có phải là hàm số bậc nhất không? Vì sao?
Vẽ đồ thị hàm số y = -x + 2
Các bài tập về góc, đường thẳng, tam giác, tính chất của các hình. Ví dụ:
Cho tam giác ABC, biết góc A = 60o, góc B = 80o. Tính góc C.
Chứng minh rằng hai đường thẳng song song khi và chỉ khi góc so le trong bằng nhau.
Ngoài đề thi giữa kì 2 Toán 7 - Đề số 1 - Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau:
Đề thi giữa kì 2 Toán 7 - Đề số 1 - Cánh diều là một cơ hội tốt để học sinh đánh giá năng lực của bản thân và chuẩn bị tốt nhất cho các kỳ thi tiếp theo. Chúc các em học sinh ôn tập tốt và đạt kết quả cao!