Chào mừng các em học sinh đến với đề thi học kì 1 Toán 7 - Đề số 3, thuộc chương trình Cánh diều.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 1 môn Toán 7.
Với cấu trúc đề thi bám sát chương trình học và đáp án chi tiết, giaitoan.edu.vn hy vọng sẽ là công cụ hỗ trợ đắc lực cho các em trong quá trình học tập.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
I. Phần trắc nghiệm (3 điểm)
1.D | 2.A | 3.C | 4.A | 5.B | 6.B | 7.D | 8.B | 9.A | 10.D |
Câu 1
Phương pháp:
Chỉ tồn tại căn bậc hai số học của số x không âm.
Cách giải:
\(\sqrt x = 4 \Leftrightarrow x = 16\)
Chọn D.
Câu 2
Phương pháp:
Nếu y liên hệ với x theo công thức y = k.x thì y tỉ lệ thuận với x theo k.
Cách giải:
Ta có y = 3. x nên k = 3
Chọn A.
Câu 3
Phương pháp:
Số đối của a là - a
Cách giải:
Số đối của \(\dfrac{{ - 1}}{2}\) là \(\dfrac{1}{2} = - \dfrac{{ - 5}}{{10}}\)
Chọn C.
Câu 4
Phương pháp:
\(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,khi\,\,x \ge 0\\ - x\,\,khi\,\,x < 0\end{array} \right.\)
Cách giải:
\(\left| { - 0,55} \right| = 0,55\)
Chọn A.
Câu 5
Phương pháp:
So sánh số thập phân thứ 4 với số 5.
Cách giải:
Số thập phân thứ 3 là 2 và số thập phân thứ 4 là số 5 nên kết quả làm tròn bằng 6,672
Chọn B.
Câu 6
Phương pháp:
\({a^m}.{a^n} = {a^{m + n}}\)
Cách giải:
\({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3} = {\left( {\dfrac{1}{2}} \right)^{2 + 3}} = {\left( {\dfrac{1}{2}} \right)^5}\)
Chọn B.
Câu 7
Phương pháp:
Hình lăng trụ đứng có 6 mặt, 8 đỉnh, 12 cạnh, 4 mặt bên, 2 mặt đáy
Cách giải:
Hình lăng trụ đứng có 6 mặt, 8 đỉnh, 12 cạnh, 4 mặt bên, 2 mặt đáy.
Chọn D.
Câu 8
Phương pháp:
Định lý từ vuông góc đến song song
Cách giải:
Vì a và c cùng vuông góc với b nên ta suy ra a // c.
Chọn B.
Câu 9
Phương pháp:
Dùng tính chất của tia phân giác
Cách giải:
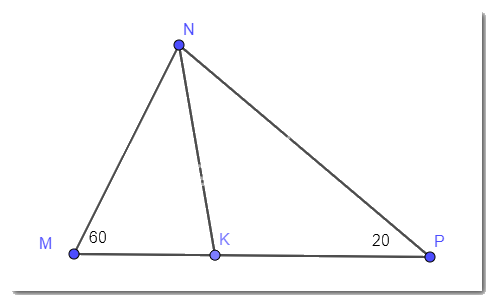
\(\begin{array}{l}\angle MNP = {180^0} - \angle N - \angle P = 180 - 60 - 20 = 100\\ \Rightarrow \angle MNK = 100:2 = 50\\ \Rightarrow \angle MKN = \angle M + \angle MNK = 60 + 50 = 110\end{array}\)
Chọn A.
Câu 10
Phương pháp:
Diện tích toàn phần hình hộp chữ nhật bằng chu vi đáy nhân chiều cao.
Cách giải:
Diện tích toàn phần bằng (80 + 50).2.35 = 9100
Chọn D.
II. Phần tự luận (7 điểm)
Câu 1
Phương pháp:
Áp dụng tính toán theo thứ tự thực hiện phép tính.
Cách giải:
a. \(\dfrac{2}{7} + \left( {\dfrac{{ - 17}}{7}} \right) + \dfrac{8}{7}\)\( = \dfrac{{2 + ( - 17) + 8}}{7} = \dfrac{{ - 7}}{7} = - 1\)
b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} - \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} - \dfrac{2}{3}} \right) = \dfrac{5}{9}:\dfrac{{ - 3}}{{22}} + \dfrac{5}{9}:\dfrac{{ - 3}}{5} = \dfrac{5}{9}.\dfrac{{ - 22}}{3} + \dfrac{5}{9}.\dfrac{{ - 5}}{3}\)
\( = \left( {\dfrac{{ - 22}}{3} + \dfrac{{ - 5}}{3}} \right).\dfrac{5}{9} = ( - 9).\dfrac{5}{9} = - 5\)
c. \(\dfrac{{{{\left( { - 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} - 1} \right| + {2023^0} = \dfrac{{ - 8}}{5}.\left| {\dfrac{{ - 3}}{4}} \right| + 1\)\( = \dfrac{{ - 8}}{5}.\dfrac{3}{4} + 1 = \dfrac{{ - 6}}{5} + 1 = \dfrac{{ - 1}}{5}\)
d. \( - \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}} - {2^2}.\left| { - \dfrac{1}{4}} \right|\)=\( - \dfrac{5}{2}.\dfrac{3}{5} - 4.\dfrac{1}{4}\)=\( - \dfrac{3}{2} - 1\)=\( - \dfrac{5}{2}\)
Câu 2
Phương pháp:
\(\left| x \right| = a\,\) với \((a > 0)\)\( \Leftrightarrow \left[ \begin{array}{l}x = a\\x = - a\end{array} \right.\)
\({x^2} = a\,\)với \((a > 0)\) \( \Leftrightarrow \left[ \begin{array}{l}x = \sqrt a \\x = - \sqrt a \end{array} \right.\)
Cách giải:
a. \(x + 1\dfrac{1}{2} = - 5,6 \Leftrightarrow x + 1,5 = - 5,6 \Leftrightarrow x = - 5,6 - 1,5 \Leftrightarrow x = \, - 7,1\)
b. \(\,\,\left| {x - \dfrac{1}{4}} \right| = \dfrac{5}{4} \Rightarrow \left[ \begin{array}{l}x - \dfrac{1}{4} = \dfrac{5}{4}\\x - \dfrac{1}{4} = - \dfrac{5}{4}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{2}\\x\,\,\,\,\,\,\,\,\,\,\, = - 1\end{array} \right.\)
c. \({\left( {\dfrac{1}{5} - \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4} \Rightarrow \left[ \begin{array}{l}\dfrac{1}{5} - \dfrac{3}{2}x = \dfrac{3}{2}\\\dfrac{1}{5} - \dfrac{3}{2}x = \dfrac{{ - 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{1}{5} - \dfrac{3}{2}\\\dfrac{3}{2}x = \dfrac{1}{5} - \dfrac{{ - 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{{ - 13}}{{10}}\\\dfrac{3}{2}x = \dfrac{{17}}{{10}}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \dfrac{{ - 13}}{{15}}\\x = \dfrac{{17}}{{15}}\end{array} \right.\)
Câu 3
Phương pháp:
Đưa về dãy tỉ số bằng nhau.
Cách giải:
Gọi a, b, c lần lượt là số HS của 3 lớp 7A, 7B, 7C (a,b,c \( \in \) N* ; a, b, c < 94)
Do khối lượng công việc của ba lớp là như nhau nên số HS và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch. Khi đó ta có: 3a = 4b = 5c và a + b + c = 94
\(3a = 4b = 5c\,\, \Leftrightarrow \,\,\dfrac{a}{{20}} = \dfrac{b}{{15}} = \dfrac{c}{{12}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{{20}} = \dfrac{b}{{15}} = \dfrac{c}{{12}} = \dfrac{{a + b + c}}{{20 + 15 + 12}} = \dfrac{{94}}{{47}} = 2\)
\(\begin{array}{l} \Rightarrow a = 2.20 = 40\\ \Rightarrow b = 2.15 = 30\\ \Rightarrow c = 2.12 = 24\end{array}\)
Vậy số của ba lớp 7A, 7B, 7C lần lượt là : 40, 30, 24.
Câu 4
Phương pháp:
Cần chia ngôi nhà ra làm hai phần:
+ Một phần là lăng trụ đứng: Đáy của lăng trụ này là tam giác cân, cạnh đáy 6m , chiều cao của đáy 1,2m, chiều cao lăng trụ 15m .
+ Phần còn lại là hình hộp chữ nhật: Có chiều dài 15m , rộng 6m , cao 3,5m .
Cách giải:
Cần chia ngôi nhà ra làm hai phần:
+ Một phần là lăng trụ đứng: Đáy của lăng trụ này là tam giác cân, cạnh đáy 6, chiều cao của đáy 1,2m; chiều cao lăng trụ 15m.
+ Phần còn lại là hình hộp chữ nhật: Có chiều dài 15m , rộng 6m , cao 3,5m
Diện tích đáy của lăng trụ có đáy là tam giác là: 1,2.6:2=3,6\({m^2}\)
Thể tích lăng trụ có đáy tam giác là: 15.3,6=54\({m^2}\)
Thể tích đáy hình chữ nhật là: 3,5.6=21\({m^2}\)
Thể tích hình hộp chữ nhật là 21. 15=315\({m^2}\)
Vậy thể tích ngôi nhà là 315 + 54 = 369\({m^2}\)
Câu 5
Phương pháp:
Đưa về lũy thừa cùng cơ số hoặc cùng số mũ để so sánh.
Cách giải:
Ta có: \({4^{30}} = {2^{30}}{.2^{30}} = {\left( {{2^3}} \right)^{10}}.{\left( {{2^2}} \right)^{15}} > {8^{10}}{.3^{15}} > \left( {{8^{10}}{{.3}^{10}}} \right).3 > {24^{10}}.3\)
Vậy \({2^{30}} + {3^{30}} + {4^{30}}\) > \({3.24^{10}}\).
Phần I: Trắc nghiệm (3 điểm).
Câu 1: Nếu \(\sqrt x = 4\) thì x bằng
A. 2
B. 4
C. \( \pm \)2
D. 16
Câu 2: Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 15. Hệ số tỉ lệ k của y đối với x là:
A. 3
B. 75
C. \(\dfrac{1}{3}\)
D. 10
Câu 3: Trong các phân số sau đây, phân số nào biểu diễn số hữu tỉ \(\dfrac{{ - 1}}{2}\).
A. \(\dfrac{{ - 2}}{4}\)
B. \(\dfrac{{ - 22}}{{48}}\)
C. \( - \dfrac{{ - 5}}{{10}}\)
D. \(\dfrac{{ - 6}}{{18}}\)
Câu 4: Cách viết nào dưới đây là đúng?
A. \(\left| { - 0,55} \right| = 0,55\)
B. \(\left| {0,55} \right| = - 0,55\)
C. \(\left| { - 0,55} \right| = - 0,55\)
D. \( - \left| {0,55} \right| = 0,55\)
Câu 5: Cho \(x = 6,67254\). Khi làm tròn đến chữ số thập phân thứ ba thì số x là:
A. \(6,672\)
B. \(6,672\)
C. \(6,67\)
D. \(6,6735\)
Câu 6: Kết quả của phép tính: \({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3}\)bằng:
A. \({\left( {\dfrac{1}{2}} \right)^2}.\)
B. \({\left( {\dfrac{1}{2}} \right)^5}\)
C. \({\left( {\dfrac{1}{2}} \right)^3}\)
D. \(\dfrac{1}{2}\)
Câu 7: Cho hình lăng trụ dưới đây. Chọn đáp án sai:
A. Hình lăng trụ đứng có tất cả 6 mặt
B. Hình lăng trụ đứng có tất cả 8 đỉnh
C. Hình lăng trụ đứng có tất cả 12 cạnh
D. Hình lăng trụ đứng có 6 mặt bên
Câu 8: Cho a\( \bot \)b và b\( \bot \)c thì:
A. a // b
B. a // c
C. b // c
D. a // b // c
Câu 9: Tam giác MNP có \(\angle M = {60^0}\), \(\angle N = {20^0}\), NK là tia phân giác. Số đo của góc \(\widehat {NKP}\) bằng:
A. 110
B. 100
C. 70
D. 30
Câu 10: Cho hình hộp chữ nhật có kích thước như hình vẽ. Diện tích toàn phần hình hộp chữ nhật là:
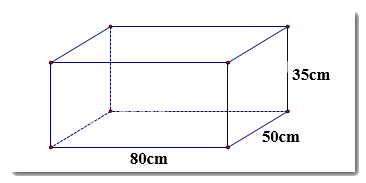
A. 140000
B. 4000
C. 260
D. 9100
Phần II: Tự luận (7 điểm).
Câu 1: (2 điểm) Thực hiện phép tính:
a. \(\dfrac{2}{7} + \left( {\dfrac{{ - 17}}{7}} \right) + \dfrac{8}{7}\)
b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} - \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} - \dfrac{2}{3}} \right).\)
c. \(\dfrac{{{{\left( { - 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} - 1} \right| + {2023^0}\).
d. \( - \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}} - {2^2}.\left| { - \dfrac{1}{4}} \right|\)
Câu 2: (1,5 điểm) Tìm x
a. \(\,x + 1\dfrac{1}{2} = - 5,6\)
b. \(\,\,\left| {x - \dfrac{1}{4}} \right| = \dfrac{5}{4}\)
c. \({\left( {\dfrac{1}{5} - \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4}\)
Câu 3: (1,5 điểm) Ba lớp 7A, 7B và 7C đi lao động và được phân công khối lượng công việc như nhau. Lớp 7A hoàn thành công việc trong 3 giờ, lớp 7B hoàn thành công việc trong 4 giờ và lớp 7C hoàn thành công việc trong 5 giờ. Tính số học sinh của mỗi lớp, biết rằng tổng số học sinh của ba lớp là 94 học sinh (giả sử năng suất làm việc của mỗi học sinh đều như nhau).
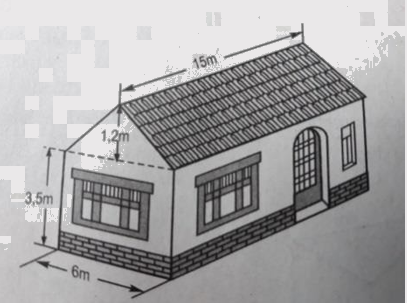
Câu 4: (1,5 điểm) Tính thể tích phần không gian của ngôi nhà có dạng một lăng trụ đứng theo các kích thước đã cho ở hình vẽ sau.
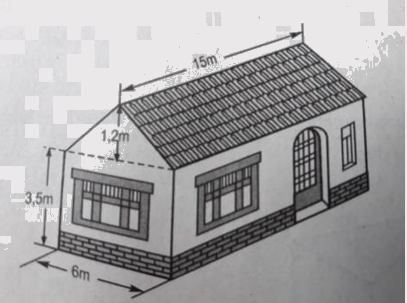
Câu 5: (0,5 điểm) So sánh \({2^{30}} + {3^{30}} + {4^{30}}\) và \({3.24^{10}}\)
Phần I: Trắc nghiệm (3 điểm).
Câu 1: Nếu \(\sqrt x = 4\) thì x bằng
A. 2
B. 4
C. \( \pm \)2
D. 16
Câu 2: Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 15. Hệ số tỉ lệ k của y đối với x là:
A. 3
B. 75
C. \(\dfrac{1}{3}\)
D. 10
Câu 3: Trong các phân số sau đây, phân số nào biểu diễn số hữu tỉ \(\dfrac{{ - 1}}{2}\).
A. \(\dfrac{{ - 2}}{4}\)
B. \(\dfrac{{ - 22}}{{48}}\)
C. \( - \dfrac{{ - 5}}{{10}}\)
D. \(\dfrac{{ - 6}}{{18}}\)
Câu 4: Cách viết nào dưới đây là đúng?
A. \(\left| { - 0,55} \right| = 0,55\)
B. \(\left| {0,55} \right| = - 0,55\)
C. \(\left| { - 0,55} \right| = - 0,55\)
D. \( - \left| {0,55} \right| = 0,55\)
Câu 5: Cho \(x = 6,67254\). Khi làm tròn đến chữ số thập phân thứ ba thì số x là:
A. \(6,672\)
B. \(6,672\)
C. \(6,67\)
D. \(6,6735\)
Câu 6: Kết quả của phép tính: \({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3}\)bằng:
A. \({\left( {\dfrac{1}{2}} \right)^2}.\)
B. \({\left( {\dfrac{1}{2}} \right)^5}\)
C. \({\left( {\dfrac{1}{2}} \right)^3}\)
D. \(\dfrac{1}{2}\)
Câu 7: Cho hình lăng trụ dưới đây. Chọn đáp án sai:
A. Hình lăng trụ đứng có tất cả 6 mặt
B. Hình lăng trụ đứng có tất cả 8 đỉnh
C. Hình lăng trụ đứng có tất cả 12 cạnh
D. Hình lăng trụ đứng có 6 mặt bên
Câu 8: Cho a\( \bot \)b và b\( \bot \)c thì:
A. a // b
B. a // c
C. b // c
D. a // b // c
Câu 9: Tam giác MNP có \(\angle M = {60^0}\), \(\angle N = {20^0}\), NK là tia phân giác. Số đo của góc \(\widehat {NKP}\) bằng:
A. 110
B. 100
C. 70
D. 30
Câu 10: Cho hình hộp chữ nhật có kích thước như hình vẽ. Diện tích toàn phần hình hộp chữ nhật là:
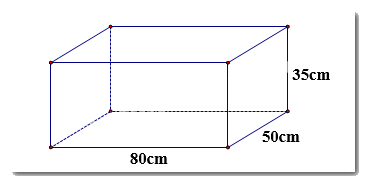
A. 140000
B. 4000
C. 260
D. 9100
Phần II: Tự luận (7 điểm).
Câu 1: (2 điểm) Thực hiện phép tính:
a. \(\dfrac{2}{7} + \left( {\dfrac{{ - 17}}{7}} \right) + \dfrac{8}{7}\)
b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} - \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} - \dfrac{2}{3}} \right).\)
c. \(\dfrac{{{{\left( { - 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} - 1} \right| + {2023^0}\).
d. \( - \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}} - {2^2}.\left| { - \dfrac{1}{4}} \right|\)
Câu 2: (1,5 điểm) Tìm x
a. \(\,x + 1\dfrac{1}{2} = - 5,6\)
b. \(\,\,\left| {x - \dfrac{1}{4}} \right| = \dfrac{5}{4}\)
c. \({\left( {\dfrac{1}{5} - \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4}\)
Câu 3: (1,5 điểm) Ba lớp 7A, 7B và 7C đi lao động và được phân công khối lượng công việc như nhau. Lớp 7A hoàn thành công việc trong 3 giờ, lớp 7B hoàn thành công việc trong 4 giờ và lớp 7C hoàn thành công việc trong 5 giờ. Tính số học sinh của mỗi lớp, biết rằng tổng số học sinh của ba lớp là 94 học sinh (giả sử năng suất làm việc của mỗi học sinh đều như nhau).
Câu 4: (1,5 điểm) Tính thể tích phần không gian của ngôi nhà có dạng một lăng trụ đứng theo các kích thước đã cho ở hình vẽ sau.
Câu 5: (0,5 điểm) So sánh \({2^{30}} + {3^{30}} + {4^{30}}\) và \({3.24^{10}}\)
I. Phần trắc nghiệm (3 điểm)
1.D | 2.A | 3.C | 4.A | 5.B | 6.B | 7.D | 8.B | 9.A | 10.D |
Câu 1
Phương pháp:
Chỉ tồn tại căn bậc hai số học của số x không âm.
Cách giải:
\(\sqrt x = 4 \Leftrightarrow x = 16\)
Chọn D.
Câu 2
Phương pháp:
Nếu y liên hệ với x theo công thức y = k.x thì y tỉ lệ thuận với x theo k.
Cách giải:
Ta có y = 3. x nên k = 3
Chọn A.
Câu 3
Phương pháp:
Số đối của a là - a
Cách giải:
Số đối của \(\dfrac{{ - 1}}{2}\) là \(\dfrac{1}{2} = - \dfrac{{ - 5}}{{10}}\)
Chọn C.
Câu 4
Phương pháp:
\(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,khi\,\,x \ge 0\\ - x\,\,khi\,\,x < 0\end{array} \right.\)
Cách giải:
\(\left| { - 0,55} \right| = 0,55\)
Chọn A.
Câu 5
Phương pháp:
So sánh số thập phân thứ 4 với số 5.
Cách giải:
Số thập phân thứ 3 là 2 và số thập phân thứ 4 là số 5 nên kết quả làm tròn bằng 6,672
Chọn B.
Câu 6
Phương pháp:
\({a^m}.{a^n} = {a^{m + n}}\)
Cách giải:
\({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3} = {\left( {\dfrac{1}{2}} \right)^{2 + 3}} = {\left( {\dfrac{1}{2}} \right)^5}\)
Chọn B.
Câu 7
Phương pháp:
Hình lăng trụ đứng có 6 mặt, 8 đỉnh, 12 cạnh, 4 mặt bên, 2 mặt đáy
Cách giải:
Hình lăng trụ đứng có 6 mặt, 8 đỉnh, 12 cạnh, 4 mặt bên, 2 mặt đáy.
Chọn D.
Câu 8
Phương pháp:
Định lý từ vuông góc đến song song
Cách giải:
Vì a và c cùng vuông góc với b nên ta suy ra a // c.
Chọn B.
Câu 9
Phương pháp:
Dùng tính chất của tia phân giác
Cách giải:
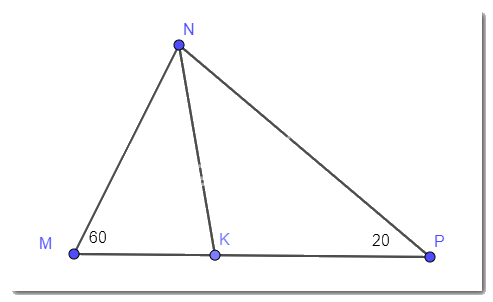
\(\begin{array}{l}\angle MNP = {180^0} - \angle N - \angle P = 180 - 60 - 20 = 100\\ \Rightarrow \angle MNK = 100:2 = 50\\ \Rightarrow \angle MKN = \angle M + \angle MNK = 60 + 50 = 110\end{array}\)
Chọn A.
Câu 10
Phương pháp:
Diện tích toàn phần hình hộp chữ nhật bằng chu vi đáy nhân chiều cao.
Cách giải:
Diện tích toàn phần bằng (80 + 50).2.35 = 9100
Chọn D.
II. Phần tự luận (7 điểm)
Câu 1
Phương pháp:
Áp dụng tính toán theo thứ tự thực hiện phép tính.
Cách giải:
a. \(\dfrac{2}{7} + \left( {\dfrac{{ - 17}}{7}} \right) + \dfrac{8}{7}\)\( = \dfrac{{2 + ( - 17) + 8}}{7} = \dfrac{{ - 7}}{7} = - 1\)
b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} - \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} - \dfrac{2}{3}} \right) = \dfrac{5}{9}:\dfrac{{ - 3}}{{22}} + \dfrac{5}{9}:\dfrac{{ - 3}}{5} = \dfrac{5}{9}.\dfrac{{ - 22}}{3} + \dfrac{5}{9}.\dfrac{{ - 5}}{3}\)
\( = \left( {\dfrac{{ - 22}}{3} + \dfrac{{ - 5}}{3}} \right).\dfrac{5}{9} = ( - 9).\dfrac{5}{9} = - 5\)
c. \(\dfrac{{{{\left( { - 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} - 1} \right| + {2023^0} = \dfrac{{ - 8}}{5}.\left| {\dfrac{{ - 3}}{4}} \right| + 1\)\( = \dfrac{{ - 8}}{5}.\dfrac{3}{4} + 1 = \dfrac{{ - 6}}{5} + 1 = \dfrac{{ - 1}}{5}\)
d. \( - \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}} - {2^2}.\left| { - \dfrac{1}{4}} \right|\)=\( - \dfrac{5}{2}.\dfrac{3}{5} - 4.\dfrac{1}{4}\)=\( - \dfrac{3}{2} - 1\)=\( - \dfrac{5}{2}\)
Câu 2
Phương pháp:
\(\left| x \right| = a\,\) với \((a > 0)\)\( \Leftrightarrow \left[ \begin{array}{l}x = a\\x = - a\end{array} \right.\)
\({x^2} = a\,\)với \((a > 0)\) \( \Leftrightarrow \left[ \begin{array}{l}x = \sqrt a \\x = - \sqrt a \end{array} \right.\)
Cách giải:
a. \(x + 1\dfrac{1}{2} = - 5,6 \Leftrightarrow x + 1,5 = - 5,6 \Leftrightarrow x = - 5,6 - 1,5 \Leftrightarrow x = \, - 7,1\)
b. \(\,\,\left| {x - \dfrac{1}{4}} \right| = \dfrac{5}{4} \Rightarrow \left[ \begin{array}{l}x - \dfrac{1}{4} = \dfrac{5}{4}\\x - \dfrac{1}{4} = - \dfrac{5}{4}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{2}\\x\,\,\,\,\,\,\,\,\,\,\, = - 1\end{array} \right.\)
c. \({\left( {\dfrac{1}{5} - \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4} \Rightarrow \left[ \begin{array}{l}\dfrac{1}{5} - \dfrac{3}{2}x = \dfrac{3}{2}\\\dfrac{1}{5} - \dfrac{3}{2}x = \dfrac{{ - 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{1}{5} - \dfrac{3}{2}\\\dfrac{3}{2}x = \dfrac{1}{5} - \dfrac{{ - 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{{ - 13}}{{10}}\\\dfrac{3}{2}x = \dfrac{{17}}{{10}}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \dfrac{{ - 13}}{{15}}\\x = \dfrac{{17}}{{15}}\end{array} \right.\)
Câu 3
Phương pháp:
Đưa về dãy tỉ số bằng nhau.
Cách giải:
Gọi a, b, c lần lượt là số HS của 3 lớp 7A, 7B, 7C (a,b,c \( \in \) N* ; a, b, c < 94)
Do khối lượng công việc của ba lớp là như nhau nên số HS và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch. Khi đó ta có: 3a = 4b = 5c và a + b + c = 94
\(3a = 4b = 5c\,\, \Leftrightarrow \,\,\dfrac{a}{{20}} = \dfrac{b}{{15}} = \dfrac{c}{{12}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{{20}} = \dfrac{b}{{15}} = \dfrac{c}{{12}} = \dfrac{{a + b + c}}{{20 + 15 + 12}} = \dfrac{{94}}{{47}} = 2\)
\(\begin{array}{l} \Rightarrow a = 2.20 = 40\\ \Rightarrow b = 2.15 = 30\\ \Rightarrow c = 2.12 = 24\end{array}\)
Vậy số của ba lớp 7A, 7B, 7C lần lượt là : 40, 30, 24.
Câu 4
Phương pháp:
Cần chia ngôi nhà ra làm hai phần:
+ Một phần là lăng trụ đứng: Đáy của lăng trụ này là tam giác cân, cạnh đáy 6m , chiều cao của đáy 1,2m, chiều cao lăng trụ 15m .
+ Phần còn lại là hình hộp chữ nhật: Có chiều dài 15m , rộng 6m , cao 3,5m .
Cách giải:
Cần chia ngôi nhà ra làm hai phần:
+ Một phần là lăng trụ đứng: Đáy của lăng trụ này là tam giác cân, cạnh đáy 6, chiều cao của đáy 1,2m; chiều cao lăng trụ 15m.
+ Phần còn lại là hình hộp chữ nhật: Có chiều dài 15m , rộng 6m , cao 3,5m
Diện tích đáy của lăng trụ có đáy là tam giác là: 1,2.6:2=3,6\({m^2}\)
Thể tích lăng trụ có đáy tam giác là: 15.3,6=54\({m^2}\)
Thể tích đáy hình chữ nhật là: 3,5.6=21\({m^2}\)
Thể tích hình hộp chữ nhật là 21. 15=315\({m^2}\)
Vậy thể tích ngôi nhà là 315 + 54 = 369\({m^2}\)
Câu 5
Phương pháp:
Đưa về lũy thừa cùng cơ số hoặc cùng số mũ để so sánh.
Cách giải:
Ta có: \({4^{30}} = {2^{30}}{.2^{30}} = {\left( {{2^3}} \right)^{10}}.{\left( {{2^2}} \right)^{15}} > {8^{10}}{.3^{15}} > \left( {{8^{10}}{{.3}^{10}}} \right).3 > {24^{10}}.3\)
Vậy \({2^{30}} + {3^{30}} + {4^{30}}\) > \({3.24^{10}}\).
Đề thi học kì 1 Toán 7 - Đề số 3, chương trình Cánh diều, là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, và các ứng dụng thực tế của toán học.
Thông thường, đề thi sẽ được chia thành các phần sau:
Tỷ lệ điểm giữa hai phần có thể khác nhau tùy theo quy định của từng trường, nhưng thường phần tự luận chiếm tỷ lệ cao hơn.
Phần này thường bao gồm các bài tập về:
Các bài tập trong phần này thường liên quan đến:
Học sinh cần nắm vững các kiến thức về:
Phần này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán liên quan đến các tình huống thực tế, như tính tiền, tính diện tích, tính thể tích, v.v.
Để đạt kết quả tốt trong kỳ thi, học sinh cần:
Ngoài việc giải đề thi, học sinh có thể tham khảo thêm các tài liệu ôn tập sau:
Hãy dành thời gian ôn tập một cách khoa học và hợp lý. Đừng quá căng thẳng, hãy giữ tinh thần thoải mái và tự tin. Chúc các em đạt kết quả tốt trong kỳ thi học kì 1!