Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán chương trình Cánh diều - Đề số 17.
Đề thi này được biên soạn bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Hãy tải đề thi về và thử sức ngay để đánh giá năng lực của bản thân nhé!
Trong các khẳng định sau, khẳng định đúng là:
\(3 \in \mathbb{Q}\).
\(1\frac{1}{5} \notin \mathbb{Q}\).
\(\frac{2}{3} \in \mathbb{N}\).
\( - \frac{1}{7} \in \mathbb{Z}\).
Căn bậc hai số học của 121 là:
-11.
11.
11 và -11.
\({11^2}\).
Diện tích của đất nước Việt Nam là \(331690k{m^2}\). Làm tròn số này với độ chính xác là \(d = 500\) được số
331 600.
332 000.
331 700.
331 000.
Cho hình lăng trụ đứng tam giác ABC.DEF như hình vẽ.
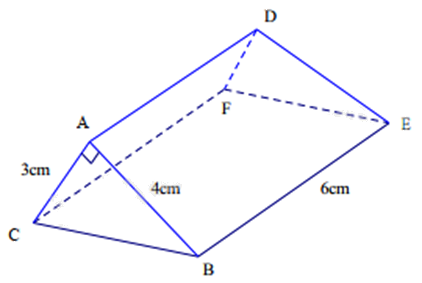
Biết AB = 4cm, AC = 3cm, BE = 6cm. Thể tích hình lăng trụ đó bằng
\(20c{m^3}\).
\(36c{m^3}\).
\(26c{m^3}\).
\(9c{m^3}\).
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 45^\circ \), số đo \(\widehat {yOz}\) bằng:
\(45^\circ \).
\(55^\circ \).
\(105^\circ \).
\(135^\circ \).
Cho hình vẽ, biết \(\widehat {{A_2}} = 68^\circ \). Tính số đo \(\widehat {{A_3}}\).
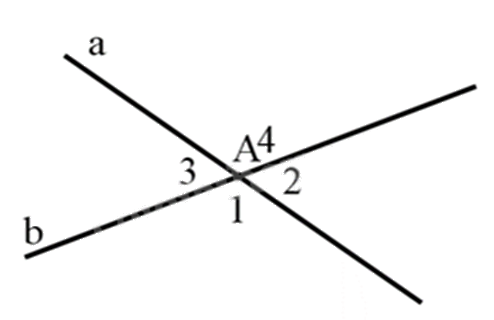
\(\widehat {{A_3}} = 112^\circ \).
\(\widehat {{A_3}} = 68^\circ \).
\(\widehat {{A_3}} = 34^\circ \).
\(\widehat {{A_3}} = 86^\circ \).
Nếu \(MN//a\) và \(MK//a\) thì theo tiên đề Euclid, ta có:
ba điểm M, N, K tạo thành tam giác.
MN song song với MK.
ba điểm M, N, K cùng nằm trên một đường thẳng.
MN vuông góc với MK.
Nếu \(a//b\) và \(b \bot c\) thì
\(a \bot b\).
\(a \bot c\).
\(a//c\).
\(b//c\).
Chọn câu trả lời đúng:
\(\left| { - 3,5} \right| = - 3,5\).
\(\left| { - 3,5} \right| = 3,5\).
\(\left| { - 3,5} \right| = \pm 3,5\).
\(\left| { - 3,5} \right| = - \frac{3}{5}\).
Từ đẳng thức \(m.n = p.q\) ta lập được tỉ lệ thức nào sau đây?
\(\frac{m}{n} = \frac{p}{q}\).
\(\frac{q}{m} = \frac{p}{n}\).
\(\frac{m}{p} = \frac{q}{n}\).
\(\frac{m}{p} = \frac{n}{q}\).
Biết \(x\) và \(y\) là hai đại lượng tỉ lệ thuận với \(x = 5\) và \(y = 15\). Hệ số tỉ lệ k của y đối với x là
\(\frac{1}{3}\).
20.
3.
75.
Biết x tỉ lệ nghịch với y theo hệ số tỉ lệ \(\frac{2}{3}\). Vậy y tỉ lệ nghịch với x theo hệ số tỉ lệ là:
\( - \frac{2}{3}\).
\(\frac{3}{2}\).
\( - \frac{3}{2}\).
\(\frac{2}{3}\).
a) Thực hiện phép tính: \(\frac{2}{3} + \left( { - \frac{3}{2}} \right).\left( { - \frac{4}{{10}}} \right)\)
b) Làm tròn số \( - 4,3615\) với độ chính xác \(d = 0,05\)
Tìm x, biết:
a) \(\frac{4}{9} - \frac{2}{3}.x = \frac{1}{3}\)
b) \(\left| {x + \frac{1}{2}} \right| = 0\)
a) Số điểm của ba bạn An, Hòa, Bình đạt được ở vòng thi tuần thứ 11 của “đấu trường toán học” lần lượt tỉ lệ với các số 9, 10, 8. Biết rằng số điểm đạt được của Hòa nhiều hơn Bình là 6 điểm. Tính số điểm đạt được của mỗi bạn.
b) Cho \(\frac{{a + c}}{{b + d}} = \frac{{a - c}}{{b - d}}\). Chứng minh rằng \(\frac{a}{b} = \frac{c}{d}\).
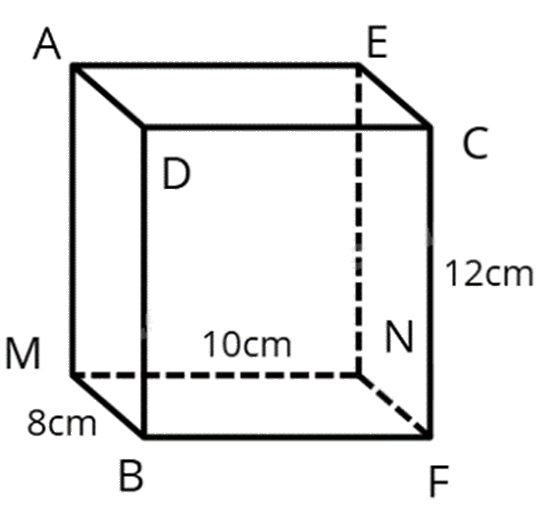
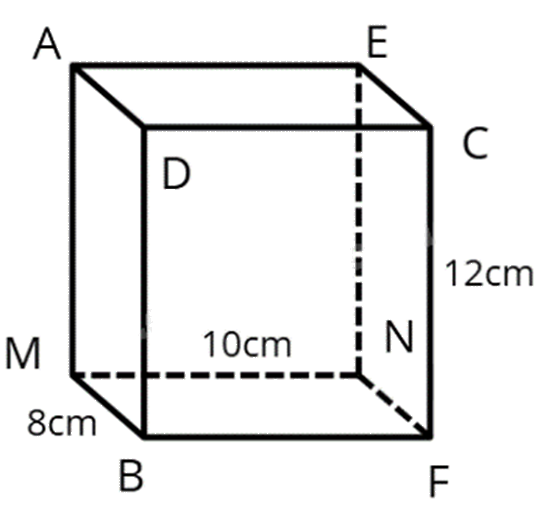
1. Một hộp quà hình hộp chữ nhật AEDC.MNFB có CF = 12cm; MN =10cm; MB = 8cm. Tính diện tích xung quanh hộp quà này
2. Cho hình vẽ, biết \(xy//mn\), \(\widehat {{A_1}} = 60^\circ \), \(xy \bot d\).
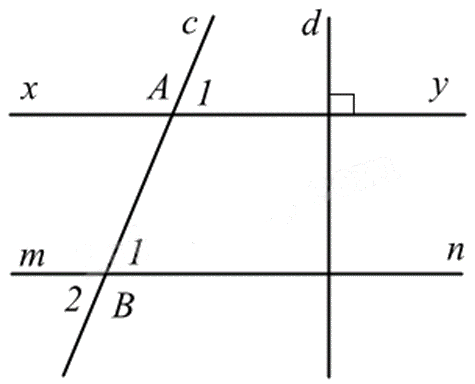
a) Chứng minh \(mn \bot d\).
b) Tính \(\widehat {{B_1}},\widehat {{B_2}}\).
c) Tia phân giác của góc mBA cắt đường thẳng xy tại K. Tính \(\widehat {mBK}\).
Viện Hàn Lâm Nhi khoa Mĩ (AAP) khuyến nghị, khối lượng cặp sách của học sinh tiểu học và trung học cơ sở không nên vượt quá 10% khối lượng cơ thể. Bạn Đức học lớp 7 có cân nặng 46 kg. Hằng ngày, bạn Đức đi học mang một chiếc cặp sách nặng 3,5 kg. Hôm nay, bạn Đức cần đem thêm một số quyển vở mới, mỗi quyển vở nặng \(\frac{4}{{25}}\) kg để tặng học sinh vùng lũ lụt. Bạn Đức có thể mang theo nhiều nhất bao nhiêu quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên?
Trong các khẳng định sau, khẳng định đúng là:
\(3 \in \mathbb{Q}\).
\(1\frac{1}{5} \notin \mathbb{Q}\).
\(\frac{2}{3} \in \mathbb{N}\).
\( - \frac{1}{7} \in \mathbb{Z}\).
Đáp án : A
Kiểm tra xem các số có thuộc tập hợp số đó hay không.
\(\mathbb{N}\) là tập hợp số tự nhiên.
\(\mathbb{Z}\) là tập hợp số nguyên.
\(\mathbb{Q}\) là tập hợp số hữu tỉ.
\(3\) là số hữu tỉ nên \(3 \in \mathbb{Q}\) là khẳng định đúng.
\(1\frac{1}{5} = \frac{6}{5}\) là số hữu tỉ nên \(1\frac{1}{5} \notin \mathbb{Q}\) là khẳng định sai.
\(\frac{2}{3}\) không phải số tự nhiên nên \(\frac{2}{3} \in \mathbb{N}\) là khẳng định sai.
\( - \frac{1}{7}\) không phải số nguyên nên \( - \frac{1}{7} \in \mathbb{Z}\) là khẳng định sai.
Đáp án A
Căn bậc hai số học của 121 là:
-11.
11.
11 và -11.
\({11^2}\).
Đáp án : B
Áp dụng kiến thức về căn bậc hai của một số: \(x = {a^2}\) thì \(\sqrt x = a\)
Căn bậc hai số học của 121 là: \(\sqrt {121} = 11\).
Đáp án B
Diện tích của đất nước Việt Nam là \(331690k{m^2}\). Làm tròn số này với độ chính xác là \(d = 500\) được số
331 600.
332 000.
331 700.
331 000.
Đáp án : B
Áp dụng quy tắc làm tròn số: Với độ chính xác là d = 500, ta làm tròn số đến hàng nghìn.
Vì 690 > 500 nên 331 690 làm tròn với độ chính xác d = 500 là 332 000.
Đáp án B
Cho hình lăng trụ đứng tam giác ABC.DEF như hình vẽ.
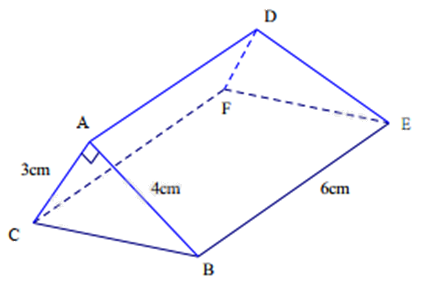
Biết AB = 4cm, AC = 3cm, BE = 6cm. Thể tích hình lăng trụ đó bằng
\(20c{m^3}\).
\(36c{m^3}\).
\(26c{m^3}\).
\(9c{m^3}\).
Đáp án : B
Thể tích hình lăng trụ là: \(V = S.h\) (S là diện tích đáy, h là chiều cao)
Diện tích đáy của hình lăng trụ là:
\(S = \frac{1}{2}.3.4 = 6\left( {c{m^2}} \right)\)
Thể tích hình lăng trụ là:
\(V = S.h = 6.6 = 36\left( {c{m^3}} \right)\).
Đáp án B
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 45^\circ \), số đo \(\widehat {yOz}\) bằng:
\(45^\circ \).
\(55^\circ \).
\(105^\circ \).
\(135^\circ \).
Đáp án : D
Tổng hai góc kề bù bằng \(180^\circ \).
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên
\(\widehat {xOy} + \widehat {yOz} = 180^\circ \)
\(\begin{array}{l}45^\circ + \widehat {yOz} = 180^\circ \\\widehat {yOz} = 180^\circ - 45^\circ \\\widehat {yOz} = 135^\circ \end{array}\)
Đáp án D
Cho hình vẽ, biết \(\widehat {{A_2}} = 68^\circ \). Tính số đo \(\widehat {{A_3}}\).
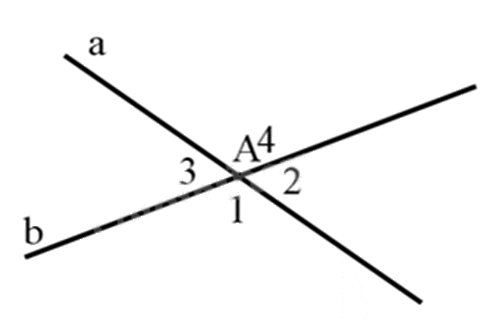
\(\widehat {{A_3}} = 112^\circ \).
\(\widehat {{A_3}} = 68^\circ \).
\(\widehat {{A_3}} = 34^\circ \).
\(\widehat {{A_3}} = 86^\circ \).
Đáp án : B
Áp dụng tính chất hai góc đối đỉnh bằng nhau.
Vì \(\widehat {{A_2}}\) và \(\widehat {{A_3}}\) là hai góc đối đỉnh nên ta có: \(\widehat {{A_3}} = \widehat {{A_2}} = 68^\circ \).
Đáp án B
Nếu \(MN//a\) và \(MK//a\) thì theo tiên đề Euclid, ta có:
ba điểm M, N, K tạo thành tam giác.
MN song song với MK.
ba điểm M, N, K cùng nằm trên một đường thẳng.
MN vuông góc với MK.
Đáp án : C
Theo tiên đề Euclid, qua một điểm nằm ngoài một đường thẳng, ta chỉ có thể kẻ được 1 đường thẳng song song với đường đó.
Nếu \(MN//a\) và \(MK//a\) thì MN trùng với MK (vì qua điểm M ta chỉ có một đường thẳng song song với a)
Do đó M, N, K cùng nằm trên một đường thẳng.
Đáp án C
Nếu \(a//b\) và \(b \bot c\) thì
\(a \bot b\).
\(a \bot c\).
\(a//c\).
\(b//c\).
Đáp án : B
Nếu đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
Nếu \(a//b\) và \(b \bot c\) thì \(a \bot c\).
Đáp án B
Chọn câu trả lời đúng:
\(\left| { - 3,5} \right| = - 3,5\).
\(\left| { - 3,5} \right| = 3,5\).
\(\left| { - 3,5} \right| = \pm 3,5\).
\(\left| { - 3,5} \right| = - \frac{3}{5}\).
Đáp án : B
+ Giá trị tuyệt đối của một số dương là chính nó
+ Giá trị tuyệt đối của một số âm là số đối của nó
Ta có: \(\left| { - 3,5} \right| = 3,5\).
Đáp án B
Từ đẳng thức \(m.n = p.q\) ta lập được tỉ lệ thức nào sau đây?
\(\frac{m}{n} = \frac{p}{q}\).
\(\frac{q}{m} = \frac{p}{n}\).
\(\frac{m}{p} = \frac{q}{n}\).
\(\frac{m}{p} = \frac{n}{q}\).
Đáp án : C
Sử dụng tính chất của tỉ lệ thức
Nếu \(m.n = p.q\) thì ta có các tỉ lệ thức: \(\frac{m}{p} = \frac{q}{n}\); \(\frac{m}{q} = \frac{p}{n}\); \(\frac{p}{m} = \frac{n}{q}\); \(\frac{q}{m} = \frac{n}{p}\) nên đáp án đúng là C.
Đáp án C
Biết \(x\) và \(y\) là hai đại lượng tỉ lệ thuận với \(x = 5\) và \(y = 15\). Hệ số tỉ lệ k của y đối với x là
\(\frac{1}{3}\).
20.
3.
75.
Đáp án : C
Đại lượng y tỉ lệ thuận với x theo hệ số tỉ lệ \(k = \frac{y}{x}\).
Hệ số tỉ lệ của y đối với x là: \(k = \frac{y}{x} = \frac{{15}}{5} = 3\).
Đáp án C
Biết x tỉ lệ nghịch với y theo hệ số tỉ lệ \(\frac{2}{3}\). Vậy y tỉ lệ nghịch với x theo hệ số tỉ lệ là:
\( - \frac{2}{3}\).
\(\frac{3}{2}\).
\( - \frac{3}{2}\).
\(\frac{2}{3}\).
Đáp án : D
Khi x tỉ lệ nghịch với y theo hệ số tỉ lệ a thì y cũng tỉ lệ nghịch với x theo hệ số tỉ lệ a.
Vì x tỉ lệ nghịch với y theo hệ số tỉ lệ \(\frac{2}{3}\) nên y tỉ lệ nghịch với x theo hệ số tỉ lệ \(\frac{2}{3}\).
Đáp án D
a) Thực hiện phép tính: \(\frac{2}{3} + \left( { - \frac{3}{2}} \right).\left( { - \frac{4}{{10}}} \right)\)
b) Làm tròn số \( - 4,3615\) với độ chính xác \(d = 0,05\)
a) Sử dụng quy tắc cộng và nhân số hữu tỉ.
b) Để làm tròn số thực âm, ta sẽ làm tròn số đối của nó rồi thêm dấu “ –“ vào trước kết quả làm tròn.
a) Ta có:
\(\frac{2}{3} + \left( { - \frac{3}{2}} \right).\left( { - \frac{4}{{10}}} \right) = \frac{2}{3} + \left( { - \frac{3}{2}} \right).\left( { - \frac{2}{5}} \right) = \frac{2}{3} + \frac{3}{5} = \frac{{19}}{{15}}\)
b) Làm tròn số \( - 4,3615\) với độ chính xác d = 0,05, ta được \( - 4,4\).
Tìm x, biết:
a) \(\frac{4}{9} - \frac{2}{3}.x = \frac{1}{3}\)
b) \(\left| {x + \frac{1}{2}} \right| = 0\)
Áp dụng quy tắc chuyển vế đổi dấu.
b) Nếu \(\left| A \right| = 0\) thì A = 0.
a) \(\frac{4}{9} - \frac{2}{3}.x = \frac{1}{3}\)
\(\begin{array}{l}\frac{2}{3}x = \frac{4}{9} - \frac{1}{3}\\\frac{2}{3}x = \frac{1}{9}\\x = \frac{1}{9}:\frac{2}{3}\\x = \frac{1}{6}\end{array}\)
Vậy \(x = \frac{1}{6}\)
b) \(\left| {x + \frac{1}{2}} \right| = 0\)
\(\begin{array}{l}x + \frac{1}{2} = 0\\x = 0 - \frac{1}{2}\\x = - \frac{1}{2}\end{array}\)
Vậy \(x = - \frac{1}{2}\)
a) Số điểm của ba bạn An, Hòa, Bình đạt được ở vòng thi tuần thứ 11 của “đấu trường toán học” lần lượt tỉ lệ với các số 9, 10, 8. Biết rằng số điểm đạt được của Hòa nhiều hơn Bình là 6 điểm. Tính số điểm đạt được của mỗi bạn.
b) Cho \(\frac{{a + c}}{{b + d}} = \frac{{a - c}}{{b - d}}\). Chứng minh rằng \(\frac{a}{b} = \frac{c}{d}\).
a) Gọi số điểm của ba bạn An, Hòa, Bình đạt được lần lượt là a (điểm); b (điểm); c (điểm).
Biểu diễn dãy tỉ số bằng nhau của ba bạn theo a, b, c.
Áp dụng tính chất dãy tỉ số bằng nhau để tìm a, b, c.
b) Áp dụng tính chất dãy tỉ số bằng nhau: \(\frac{A}{B} = \frac{C}{D} = \frac{{A + C}}{{B + D}} = \frac{{A - C}}{{B - D}}\) để chứng minh \(\frac{{a + c}}{{b + d}} = \frac{{a - c}}{{b - d}} = \frac{a}{b} = \frac{c}{d}\).
a) Gọi số điểm của ba bạn An, Hòa, Bình đạt được lần lượt là a (điểm); b (điểm); c (điểm).
Vì số điểm của ba bạn An, Hòa, Bình đạt được ở vòng thi tuần thứ 11 của “đấu trường toán học” lần lượt tỉ lệ với các số 9, 10, 8 nên ta có: \(\frac{a}{9} = \frac{b}{{10}} = \frac{c}{8}\).
Vì số điểm đạt được của Hòa nhiều hơn Bình là 6 điểm nên ta có: b – c = 6.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{9} = \frac{b}{{10}} = \frac{c}{8} = \frac{{b - c}}{{10 - 8}} = \frac{6}{2} = 3\)
Suy ra a = 9.3 = 27; b = 10.3 = 30; c = 8.3 = 24.
Vậy số điểm của ba bạn An, Hòa, Bình đạt được lần lượt là 27 điểm, 30 điểm, 24 điểm.
b) Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\frac{{a + c}}{{b + d}} = \frac{{a - c}}{{b - d}} = \frac{{a + c + a - c}}{{b + d + b - d}} = \frac{{2a}}{{2b}} = \frac{a}{b}\,\left( 1 \right)\\\frac{{a + c}}{{b + d}} = \frac{{a - c}}{{b - d}} = \frac{{a + c - \left( {a - c} \right)}}{{b + d - \left( {b - d} \right)}}\frac{{a + c - a + c}}{{b + d - b + d}} = \frac{{2c}}{{2d}} = \frac{c}{d}\,\left( 2 \right)\end{array}\)
Từ (1) và (2) suy ra \(\frac{a}{b} = \frac{c}{d}\).
1. Một hộp quà hình hộp chữ nhật AEDC.MNFB có CF = 12cm; MN =10cm; MB = 8cm. Tính diện tích xung quanh hộp quà này
2. Cho hình vẽ, biết \(xy//mn\), \(\widehat {{A_1}} = 60^\circ \), \(xy \bot d\).
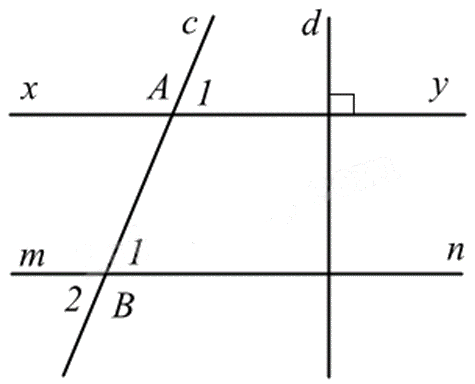
a) Chứng minh \(mn \bot d\).
b) Tính \(\widehat {{B_1}},\widehat {{B_2}}\).
c) Tia phân giác của góc mBA cắt đường thẳng xy tại K. Tính \(\widehat {mBK}\).
1. Sử dụng công thức tính diện tích xung quanh của hình hộp chữ nhật: Sxq = chu vi đáy. chiều cao.
2. a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
b) Áp dụng tính chất hai đường thẳng song song có hai góc đồng vị bằng nhau và hai góc đối đỉnh.
c) Hai góc kề bù có tổng bằng \(180^\circ \) nên ta tính được góc mBA.
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
1. Diện tích xung quanh của hộp quà là:
Sxq = 2.(10 + 8).12 = 432 (cm2).
Vậy diện tích xung quanh của hộp quà là 432cm2.
2.
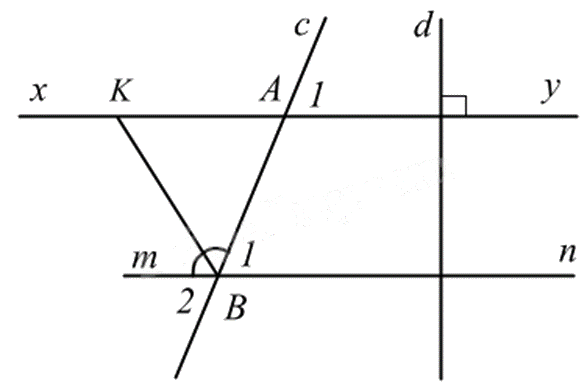
a) Vì \(xy//mn\), \(xy \bot d\) nên \(mn \bot d\).
b) Vì \(xy//mn\) nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (hai góc đồng vị) nên \(\widehat {{B_1}} = 60^\circ \).
Vì \(\widehat {{B_1}} = \widehat {{B_2}}\) (hai góc đối đỉnh) nên \(\widehat {{B_2}} = 60^\circ \).
c) Vì \(\widehat {mBA}\) và \(\widehat {{B_1}}\) là hai góc kề bù nên \(\widehat {mBA} + \widehat {{B_1}} = 180^\circ \), suy ra \(\widehat {mBA} = 180^\circ - \widehat {{B_1}} = 180^\circ - 60^\circ = 120^\circ \).
Vì BK là tia phân giác của góc mBA nên \(\widehat {mBK} = \frac{1}{2}\widehat {mBA} = \frac{1}{2}.120^\circ = 60^\circ \).
Viện Hàn Lâm Nhi khoa Mĩ (AAP) khuyến nghị, khối lượng cặp sách của học sinh tiểu học và trung học cơ sở không nên vượt quá 10% khối lượng cơ thể. Bạn Đức học lớp 7 có cân nặng 46 kg. Hằng ngày, bạn Đức đi học mang một chiếc cặp sách nặng 3,5 kg. Hôm nay, bạn Đức cần đem thêm một số quyển vở mới, mỗi quyển vở nặng \(\frac{4}{{25}}\) kg để tặng học sinh vùng lũ lụt. Bạn Đức có thể mang theo nhiều nhất bao nhiêu quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên?
Tính khối lượng cặp sách của bạn Đức khi biết cân nặng và tỉ số phần trăm khối lượng cặp sách so với cân nặng.
Từ đó tính khối lượng vở mới bạn Đức có thể mang nhiều nhất = khối lượng cặp sách – khối lượng chiếc cặp.
Tính số quyển vở tương ứng với \(\frac{4}{{25}}kg\).
Theo khuyến nghị, khối lượng cặp sách bạn Đức nên mang không vượt quá là:
46 . 10% = 4,6 (kg).
Khối lượng vở mới Đức có thể mang thêm nhiều nhất theo khuyến nghị là:
4,6 – 3,5 = 1,1 (kg).
1,1kg ứng với số quyển vở nặng \(\frac{4}{{25}}\)kg là: \(1,1:\frac{4}{{25}} = 1,1.\frac{{25}}{4} = 6,875\)
Do đó bạn Đức có thể mang theo nhiều nhất 6 quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên.
Đề thi học kì 1 Toán 7 Cánh diều - Đề số 17 là một trong những đề thi quan trọng giúp học sinh lớp 7 đánh giá kiến thức đã học trong nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của toán học.
Thông thường, đề thi học kì 1 Toán 7 Cánh diều - Đề số 17 có cấu trúc gồm các phần sau:
Để giúp các em học sinh ôn tập và làm bài thi hiệu quả, chúng tôi xin giới thiệu chi tiết nội dung đề thi học kì 1 Toán 7 Cánh diều - Đề số 17:
Phần trắc nghiệm thường bao gồm các câu hỏi về:
Phần tự luận thường bao gồm các bài tập về:
Để giúp các em học sinh hiểu rõ hơn về đề thi và cách giải các bài tập, chúng tôi xin cung cấp hướng dẫn giải chi tiết cho từng câu hỏi trong đề thi học kì 1 Toán 7 Cánh diều - Đề số 17.
Ví dụ:
Câu 1: Giải phương trình 2x + 3 = 7
Hướng dẫn giải:
Vậy nghiệm của phương trình là x = 2.
Để hỗ trợ quá trình ôn tập và làm bài thi, các em có thể tham khảo thêm các tài liệu sau:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi học kì 1!