Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 7, một công cụ ôn luyện tuyệt vời dành cho học sinh lớp 7. Đề thi được biên soạn theo chương trình Cánh diều, bám sát kiến thức trọng tâm và cấu trúc đề thi chính thức.
Đề thi này không chỉ giúp các em làm quen với dạng đề mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
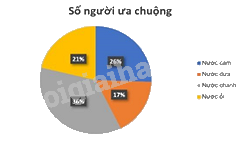
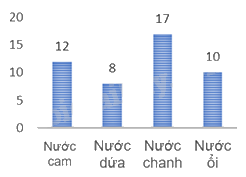
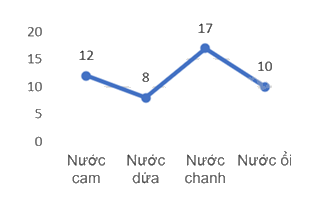
Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được bảng dữ liệu sau:

Biểu đồ đoạn thẳng để biểu diễn cho các mặt hàng ưa chuộng là:

Khi được hỏi về môn học yêu thích của một nhóm bạn lớp cho kết quả được ghi lại trong bảng như sau:

Có bao nhiêu bạn được hỏi?
Bạn Nam gieo một con xúc xắc 10 lần liên tiếp thì thấy mặt 4 chấm xuất hiện 3 lần. Xác suất xuất hiện mặt 4 chấm là
An lấy ngẫu nhiên 4 viên bi trong một túi đựng 4 bi xanh và 3 bi đỏ. Đâu là biến cố chắc chắn?
Gieo một con xúc xắc đồng chất một lần. Xác suất xuất hiện mặt có số chấm chẵn là:
Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?
Cho \(\Delta ABC = \Delta DEF\). Khi đó:
Cho \(\Delta ABC = \Delta DEF\), \(\hat C = {40^0}\). Khi đó:
Cho tam giác ABC có: \(\widehat A = {45^0};\widehat B = {60^0}\). So sánh các cạnh của tam giác ABC là:
Cho hình vẽ, hãy chỉ ra hai tam giác bằng nhau.
Cho tam giác ABC cân tại A, cạnh AB = 5cm. Tính độ dài cạnh AC?
Cho hình vẽ, có bao nhiêu đường xiên kẻ từ điểm A đến đường thẳng BF?
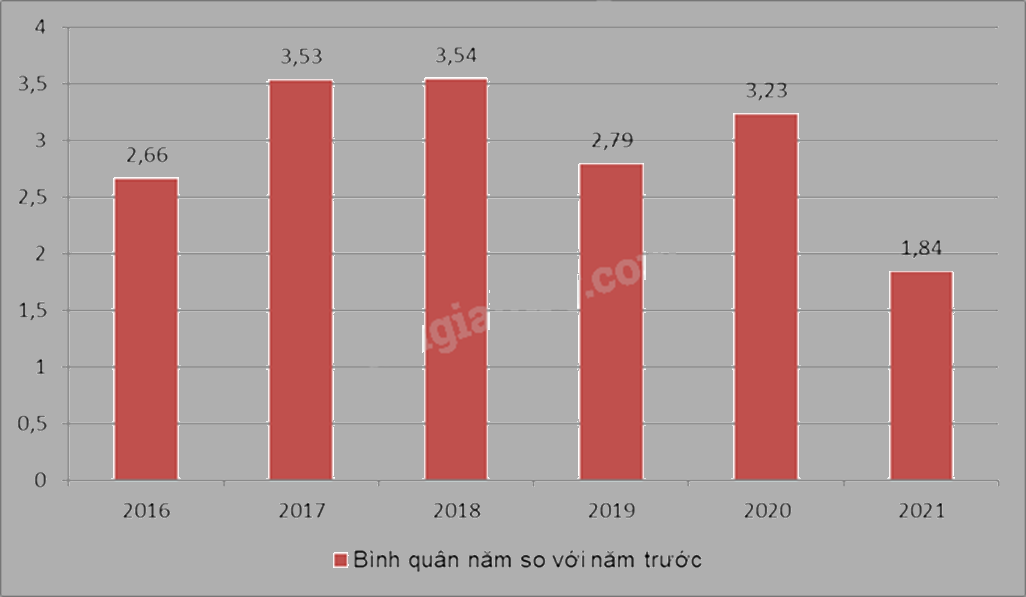
Biểu đồ hình cột biểu diễn tốc độ tăng trưởng chỉ số tiêu dùng (CPI) các năm giai đoạn 2016-2021 (%).
a) Lập bảng số liệu thống kê tốc độ tăng trưởng chỉ số tiêu dùng (CPI) các năm giai đoạn 2016-2021 theo mẫu sau:

b) Tìm năm có CPI trung bình lớn nhất?
c) Tính CPI trung bình của các năm từ 2016 đến 2021?
Một chiếc hộp có 12 thẻ cùng loại, mỗi thẻ được ghi một trong các số 1,2,3,…12. Hai thẻ khác nhau thì đánh số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xét biến cố “Số xuất hiện trên thẻ là số nguyên tố”. Tính xác suất của biến cố trên.
Một chiếc thang dựa vào tường và nghiêng với mặt đất là 500. Tính góc nghiêng của thang so với tường.

So sánh các cạnh của tam giác ABC có \(\widehat A = {50^0},\,\widehat B = {60^0}\).
Cho tam giác ABC có AB = AC, N là trung điểm của BC.
a) Chứng minh \(\Delta ABN = \Delta ACN\).
b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.
c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.
Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được bảng dữ liệu sau:

Biểu đồ đoạn thẳng để biểu diễn cho các mặt hàng ưa chuộng là:
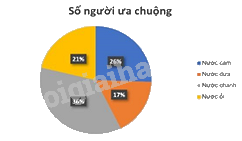
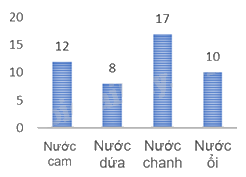
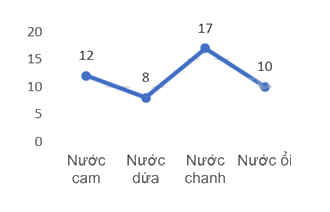

Đáp án : C
Dựa vào đặc điểm của các loại biểu đồ.
Biểu đồ đoạn thẳng là biểu đồ C.
Khi được hỏi về môn học yêu thích của một nhóm bạn lớp cho kết quả được ghi lại trong bảng như sau:

Có bao nhiêu bạn được hỏi?
Đáp án : B
Dựa vào bảng thống kế để xác định.
Trong bảng thống kê trên, ta thấy có 8 câu trả lời nên có 8 bạn được hỏi.
Bạn Nam gieo một con xúc xắc 10 lần liên tiếp thì thấy mặt 4 chấm xuất hiện 3 lần. Xác suất xuất hiện mặt 4 chấm là
Đáp án : B
Xác suất bằng tỉ số giữa số lần xuất hiện mặt 4 chấm với tổng số lần gieo.
Xác suất xuất hiện mặt 4 chấm là \(\frac{3}{{10}}\).
An lấy ngẫu nhiên 4 viên bi trong một túi đựng 4 bi xanh và 3 bi đỏ. Đâu là biến cố chắc chắn?
Đáp án : B
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra.
Biến cố A. Biến cố ngẫu nhiên.
Biến cố B. Biến cố chắc chắn.
Biến cố C. Biến cố ngẫu nhiên.
Biến cố D. Biến cố ngẫu nhiên.
Gieo một con xúc xắc đồng chất một lần. Xác suất xuất hiện mặt có số chấm chẵn là:
Đáp án : D
Xác suất xuất hiện mặt có chấm chẵn bằng tỉ số giữa số số mặt có chấm chẵn với tổng số mặt của xúc xắc.
Có 3 mặt có số chấm chẵn là 2; 4; 6.
Số mặt của xúc xắc là 6: 1; 2; 3; 4; 5; 6.
Xác suất xuất hiện mặt có số chấm chẵn là: \(\frac{3}{6} = \frac{1}{2}\).
Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?
Đáp án : C
Dựa vào quan hệ giữa ba cạnh của một tam giác.
Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại nên A, B và D đúng.
Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại nên C sai.
Cho \(\Delta ABC = \Delta DEF\). Khi đó:
Đáp án : A
Dựa vào các kiến thức về hai tam giác bằng nhau.
\(\Delta ABC = \Delta DEF\) nên ta có:
\(\begin{array}{l}AB = DE\\BC = EF\\AC = DF\end{array}\)
Cho \(\Delta ABC = \Delta DEF\), \(\hat C = {40^0}\). Khi đó:
Đáp án : A
Dựa vào các kiến thức về hai tam giác bằng nhau.
\(\Delta ABC = \Delta DEF\) nên ta có:
\(\widehat C = \widehat F = {40^0}\).
Cho tam giác ABC có: \(\widehat A = {45^0};\widehat B = {60^0}\). So sánh các cạnh của tam giác ABC là:
Đáp án : A
Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác.
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {45^0} - {60^0}\\ = {75^0}\end{array}\)
Trong tam giác ABC, ta có:
\(\widehat C > \widehat B > \widehat A\left( {{{75}^0} > {{60}^0} > {{45}^0}} \right)\) suy ra \(AB > AC > BC\).
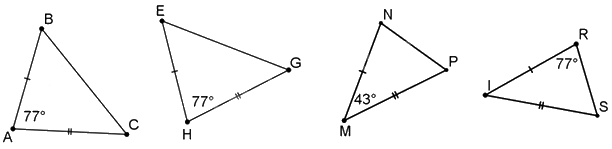
Cho hình vẽ, hãy chỉ ra hai tam giác bằng nhau.
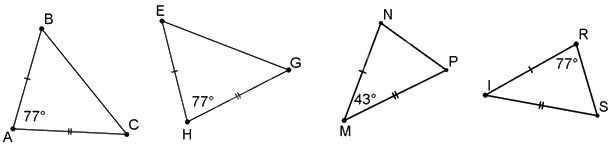
Đáp án : A
Dựa vào các trường hợp bằng nhau của hai tam giác để xác định.
Trong các tam giác trên, chỉ có \(\Delta ABC = \Delta HEG\)(c.g.c) đủ điều kiện để xác định bằng nhau.
Cho tam giác ABC cân tại A, cạnh AB = 5cm. Tính độ dài cạnh AC?
Đáp án : D
Dựa vào tính chất của tam giác cân.
Tam giác ABC cân tại A nên AB = AC = 5cm.
Cho hình vẽ, có bao nhiêu đường xiên kẻ từ điểm A đến đường thẳng BF?
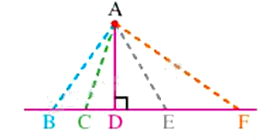
Đáp án : D
Dựa vào kiến thức về đường xiên.
Trong hình trên, có 4 đường xiên là: AB, AC, AE, AF.
Biểu đồ hình cột biểu diễn tốc độ tăng trưởng chỉ số tiêu dùng (CPI) các năm giai đoạn 2016-2021 (%).
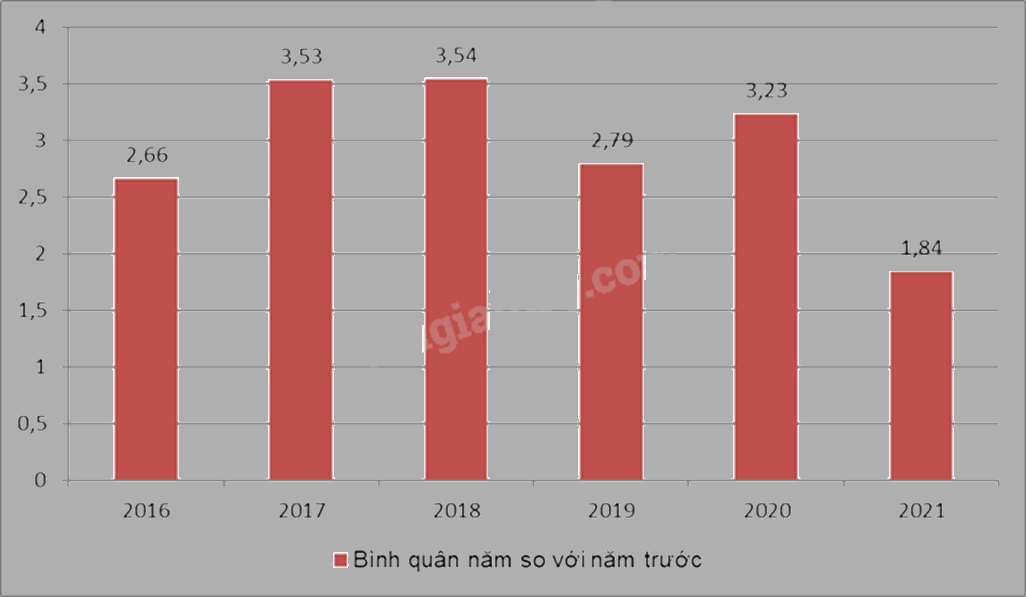
a) Lập bảng số liệu thống kê tốc độ tăng trưởng chỉ số tiêu dùng (CPI) các năm giai đoạn 2016-2021 theo mẫu sau:

b) Tìm năm có CPI trung bình lớn nhất?
c) Tính CPI trung bình của các năm từ 2016 đến 2021?
a, b) Quan sát biểu đồ để trả lời câu hỏi.
c) CPI trung bình bằng tổng số CPI chia cho số năm.
a) Bảng số liệu thống kê tốc độ tăng trưởng chỉ số tiêu dùng(CPI) các năm giai đoạn 2016-2021:

b) Năm có CPI trung bình lớn nhất là năm 2018 với CPI là 3,54%.
c) CPI trung bình của các năm từ 2016 đến 2021 là:
$\frac{2,66+3,53+3,54+2,79+3,23+1,84}{6}\approx 2,93$
Một chiếc hộp có 12 thẻ cùng loại, mỗi thẻ được ghi một trong các số 1,2,3,…12. Hai thẻ khác nhau thì đánh số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xét biến cố “Số xuất hiện trên thẻ là số nguyên tố”. Tính xác suất của biến cố trên.
Xác định số kết quả có thể, số kết quả thuận lợi cho biến cố.
Có 12 kết quả có thể xảy ra khi rút ngẫu nhiên một thẻ trong hộp, đó là: 1; 2; 3; …; 12.
Có 5 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ là số nguyên tố” là: 2; 3; 5; 7; 11.
Vậy xác suất của biến cố ‘‘Số xuất hiện trên thẻ là số nguyên tố’’ là: \(\frac{5}{{12}}\).
Một chiếc thang dựa vào tường và nghiêng với mặt đất là 500. Tính góc nghiêng của thang so với tường.

Dựa vào định lí tổng hai góc nhọn trong một tam giác vuông bằng \({90^0}\).
Gọi tam giác ABC là hình mô tả chiếc thang dựa vào tường.
Góc C là góc nghiêng của thang so với tường.
Trong tam giác ABC vuông tại A có: \(\widehat B + \widehat C = {90^0}\) (tổng hai góc nhọn trong một tam giác vuông).
Suy ra \(\widehat C = {90^0} - \widehat B = {90^0} - {50^0} = {40^0}\).
Vậy độ nghiêng của chiếc thang so với bức tường là \({40^0}\).
So sánh các cạnh của tam giác ABC có \(\widehat A = {50^0},\,\widehat B = {60^0}\).
Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác.
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {50^0} - {60^0}\\ = {70^0}\end{array}\)
Trong tam giác ABC, ta có:
\(\widehat C > \widehat B > \widehat A\left( {{{70}^0} > {{60}^0} > {{50}^0}} \right)\) suy ra \(AB > AC > BC\).
Cho tam giác ABC có AB = AC, N là trung điểm của BC.
a) Chứng minh \(\Delta ABN = \Delta ACN\).
b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.
c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.
a) Dựa vào các trường hợp bằng nhau của hai tam giác.
b) Chứng minh \(AN \bot BC\) suy ra a // BC.
c) Dựa vào bất đẳng thức tam giác để chứng minh.
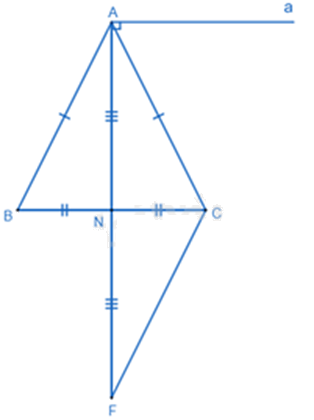
a) Xét \(\Delta ABN\) và \(\Delta ACN\) có:
\(\begin{array}{l}AB = AC(gt)\\BN = CN(gt)\\AN\,chung\end{array}\)
Suy ra \(\Delta ABN = \Delta ACN\)(c.c.c) (đpcm)
b) Ta có \(\Delta ABN = \Delta ACN\) suy ra \(\widehat {ANB} = \widehat {ANC}\).
Mà hai góc này là hai góc kề bù nên \(\widehat {ANB} = \widehat {ANC} = \frac{{{{180}^0}}}{2} = {90^0}\).
Do đó \(AN \bot BC\). Mà \(a \bot AN\) (gt)
Suy ra \(a//BC\) (từ vuông góc đến song song) (đpcm).
c) Xét \(\Delta ABN\) và \(\Delta FCN\) có:
\(\begin{array}{l}AN = NF(gt)\\BN = CN(gt)\end{array}\)
\(\widehat {ANB} = \widehat {FNC}\) (hai góc đối đỉnh)
Suy ra \(\Delta ABN = \Delta FCN\)(c.g.c) (đpcm)
Suy ra AB = CF.
Xét \(\Delta ACF\) có:
\(\begin{array}{l}CF + AC > AF\\AB + AC > 2AN\end{array}\)
(vì AB = CF và AF = 2AN) (đpcm).
Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 7 là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức của học sinh sau nửa học kỳ 2. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức, hàm số và các ứng dụng thực tế của toán học.
Thông thường, đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 7 có cấu trúc gồm:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 7:
Để giải tốt đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 7, học sinh cần nắm vững các kiến thức cơ bản, rèn luyện kỹ năng giải toán thường xuyên và làm quen với các dạng bài tập khác nhau. Dưới đây là một số lời khuyên:
Ngoài việc luyện tập giải đề thi, học sinh có thể tham khảo các tài liệu ôn thi hữu ích sau:
Để đạt kết quả tốt nhất trong kỳ thi giữa kì 2 Toán 7 Cánh diều - Đề số 7, học sinh cần chuẩn bị kỹ lưỡng về kiến thức, kỹ năng và tâm lý. Dưới đây là một số lời khuyên:
Chúc các em học sinh ôn thi tốt và đạt kết quả cao trong kỳ thi giữa kì 2 Toán 7 Cánh diều - Đề số 7!